北京市海淀区2013-2014学年高二下学期期中考试数学文试题 扫描版含答案

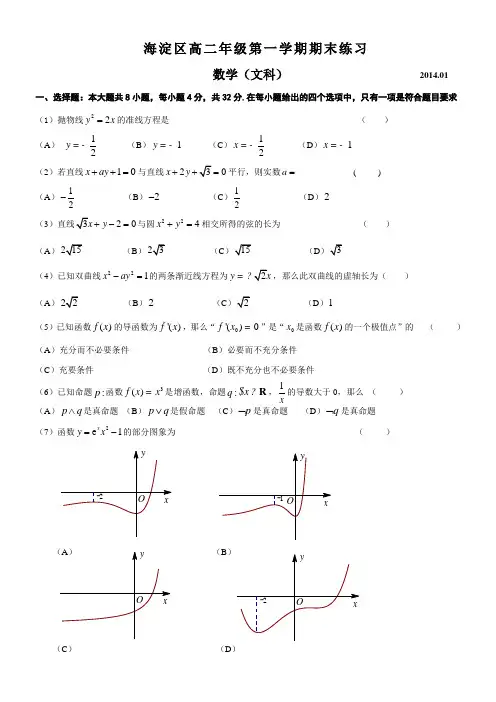
海淀区高二年级第一学期期末练习数学（文科） 2014.01一、选择题：本大题共8小题，每小题4分，共32分.在每小题给出的四个选项中，只有一项是符合题目要求 （1）抛物线22y x =的准线方程是 （ ） （A ） 12y =-（B ）1y =- （C ）12x =-（D ）1x =-（2）若直线10x ay ++=与直线20x y ++=平行，则实数a = ( ) （A ）12-（B ）2- （C ）12 （D ）2（320y +-=与圆224x y +=相交所得的弦的长为 （ ） （A） （B） （C（D（4）已知双曲线221x ay -=的两条渐近线方程为y =，那么此双曲线的虚轴长为（ ）（A） （B ）2 （C（D ）1（5）已知函数()f x 的导函数为'()f x ，那么“0'()0f x =”是“0x 是函数()f x 的一个极值点”的 （ ） （A ）充分而不必要条件 （B ）必要而不充分条件 （C ）充要条件 （D ）既不充分也不必要条件（6）已知命题:p 函数3()f x x =是增函数，命题:q x R $ ，1x的导数大于0，那么 （ ） （A ）p q ∧是真命题 （B ）p q ∨是假命题 （C ）p ⌝是真命题 （D ）q ⌝是真命题（7）函数2e 1x y x =-的部分图象为 （ ）（B （C ） （D ）（8）在平面直角坐标系xOy 中，已知集合{}2()001x,y y x ,x ≤≤≤≤且所表示的图形的面积为31，若集合},1),{(≤-=x y y x M }1),{(2+≥=x y y x N ，则N M 所表示的图形面积为（ ） （A ）31 （B ）32 （C ）1 （D ）34二、填空题：本大题共6小题，每小题4分，共24分，把答案填在题中横线上. （9）已知()cos f x x x =，则'()f x = .（10）过点(1,1)且与圆2220x x y -+=相切的直线的方程是 .（11）曲线2y ax b =+在1x =处的切线方程为41y x =-，则a =______，b =______.（12）已知抛物线C ：24y x =，O 为坐标原点，F 为C 的焦点，P 是C 上一点. 若OPF ∆是等腰三角形，则PO = .（13）已知点12,F F 是双曲线C 的两个焦点，过点2F 的直线交双曲线C 的一支于,A B 两点，若1ABF ∆为等边三角形，则双曲线C 的离心率为 .（14）如图所示，在正方体1111ABCD A B C D -中，点E 是棱1CC 上的一个动点，平面1BED 交棱1AA 于点F ．给出下列四个结论：①存在点E ，使得11A C //平面1BED F ； ②存在点E ，使得1B D ⊥平面1BED F ； ③对于任意的点E ，平面11AC D ⊥平面1BED F ；④对于任意的点E ，四棱锥11B BED F -的体积均不变. 其中，所有正确结论的序号是___________．三、解答题：本大题共4小题，共44分.解答应写出文字说明，证明过程或演算步骤. （15）（本小题共11分）已知函数321()43f x x ax =-+，且2x =是函数()f x 的一个极小值点. （Ⅰ）求实数a 的值；（Ⅱ）求)(x f 在区间[1,3]-上的最大值和最小值.F ED 1C 1B 1A 1DCA(16)（本小题共11分）已知抛物线2:4C y x =的焦点为F ，过点F 的直线l 交抛物线C 于点P ，Q . （Ⅰ）若3PF =（点P 在第一象限），求直线l 的方程；（Ⅱ）求证：OP OQ ⋅为定值（点O 为坐标原点）.(17)（本小题共11分）已知椭圆M ：22221(0)x y a b a b+=>>经过点(1,-，(0,1). （Ⅰ）求椭圆M 的方程；（Ⅱ）设椭圆M 的左、右焦点分别为12,F F ，过点2F 的直线交椭圆M 于, A B 两点，求1ABF ∆面积的最大值.(18)（本小题共11分）已知函数22()2ln (0)f x x a x a =->. （Ⅰ）求函数()f x 的单调区间；（Ⅱ）记函数()f x 的最小值为M ，求证：1M ≤.海淀区高二年级第一学期期末练习数学（文科）参考答案及评分标准 2014．01一. 选择题：本大题共8小题，每小题4分，共32分.二.填空题：本大题共6小题，每小题4分，共24分.（9）cos sin x x x - （10）10y -= （11）2，1（12）32或1 （13 （14）①③④ 注：（11）题每空2分；（12）题少一个答案扣2分.三.解答题：本大题共4小题，共44分.解答应写出文字说明，证明过程或演算步骤. （15）（本小题满分11分）解：（Ⅰ）2'()2f x x ax =-. ………………………2分2x =是函数()f x 的一个极小值点，∴'(2)0f =.即440a -=，解得1a =. ………………………4分 经检验，当1a =时，2x =是函数()f x 的一个极小值点.∴ 实数a 的值为1. ………………………5分（Ⅱ）由（Ⅰ）知，321()43f x x x =-+.2'()2(2)f x x x x x =-=-.令'()0f x =，得0x =或2x =. ………………………6分 当x 在[1,3]-上变化时，()'(),f x f x 的变化情况如下：当1x =-或2x =时，()f x 有最小值83； 当0x =或3x =时，()f x 有最大值4. ………………………11分（16）（本小题满分11分）解：（Ⅰ）设00(,)P x y ，由题意，00x >且00y >.点P 在抛物线C 上，且3PF =，∴点P 到准线1x =-的距离为3.∴013x +=，02x =. ………………………2分又 2004y x =，00y >，∴0y =∴(2,P .(1,0)F ， ………………………4分 ∴直线l的方程为1)y x =-，即y =-. ………………………5分（Ⅱ）由题意可设直线l 的方程为：1x my =+.由21,4x my y x=+⎧⎨=⎩得214y my =+，即2440y my --=. ………………………7分显然216160m ∆=+>恒成立.设11(,)P x y ，22(,)Q x y ，则12124,4.y y m y y +=⎧⎨⋅=-⎩ ………………………9分∴1212OP OQ x x y y ⋅=+1212(1)(1)my my y y =+++21212(1)()1m y y m y y =++++224(1)41m m =-+++3=-.即3OP OQ ⋅=-为定值. ………………………11分（17）（本小题满分11分）解：（Ⅰ）由题意1b =，椭圆M 的方程为2221(1)x y a a+=>. ………………………1分将点(1,-代入椭圆方程，得21112a +=，解得22a =. 所以 椭圆M 的方程为2212x y +=. ………………………3分（Ⅱ）由题意可设直线AB 的方程为：1x my =+.由221,22x my x y =+⎧⎨+=⎩得22(2)210m y my ++-=. 显然 2244(2)0m m ∆=++>.设11(,)A x y ，22(,)B x y ，则1221222,21.2m y y m y y m -⎧+=⎪⎪+⎨-⎪⋅=⎪+⎩………………………7分因为 1ABF ∆的面积12121||(||||)2S F F y y =+，其中120y y <. 所以 12121||||2S F F y y =-. 又22121212()()4y y y y y y -=+-22221422m m m --⎛⎫⎛⎫=- ⎪ ⎪++⎝⎭⎝⎭22288(2)m m +=+， 12(1,0),(1,0)F F -. ………………………9分∴2212()S y y =-2222211118[]8()222(2)22m m m =-=--+≤+++.当0m =时，上式中等号成立.即当0m =时，1ABF ∆. ………………………11分（18）（本小题满分11分） 解：（Ⅰ）22()2ln (0)f x x a x a =->的定义域为(0,)+∞.22'()2a f x x x =-2222x a x -=2()()x a x a x+-=. ………………………2分 令'()0f x =，解得x a =或x a =-（舍）.当x 在(0,)+∞内变化时，()'(),f x f x 的变化情况如下：由上表知，()f x 的单调递增区间为(,)a +∞；()f x 的单调递减区间为(0,)a .………………………5分（Ⅱ）由（Ⅰ）知，()f x 的最小值222ln M a a a =-. ………………………6分 令22()2ln (0)g x x x x x =->，则'()24ln 24ln g x x x x x x x =--=-.令'()0g x =，解得1x =. ………………………8分 当x 在(0,)+∞内变化时，()'(),g x g x 的变化情况如下：所以 函数()g x 的最大值为1，即()1g x ≤.因为0a >，所以 222ln 1M a a a =-≤. ………………………11分注：对于其它正确解法，相应给分.。

2014海淀区高二（下）期中数学（文科）一、选择题：本大题共8小题，共32分.1．（4分）已知复数z=1﹣i，那么|z|=（）A．0 B．1 C．D．22．（4分）下列推理正确的是（）A．如果不买彩票，那么就不能中奖．因为你买了彩票，所以你一定中奖B．已知三个不同的平面α，β，γ，如果α⊥β，β⊥γ，那么α⊥γC．已知非零向量，，，如果?=?，那么=D．如果复数z满足z2＞0，则z∈R3．（4分）如图结构图中，框①，②处分别填入（）A．l?α，l⊥αB．l?α，l与α相交C．l?α，l⊥αD．l?α，l与α相交4．（4分）下面是一段“三段论”推理过程：若函数f（x）在（a，b）内可导且单调递增，则在（a，b）内，f′（x）＞0恒成立．因为f（x）=x3在（﹣1，1）内可导且单调递增，所以在（﹣1，1）内，f′（x）=3x2＞0恒成立．以上推理中（）A．大前提错误B．小前提错误C．结论正确D．推理形式错误5．（4分）用反证法证明某命题时，对结论：“自然数a，b，c中恰有一个偶数”正确的假设为（）A．a，b，c都是奇数B．a，b，c都是偶数C．a，b，c中至少有两个偶数D．a，b，c中至少有两个偶数或都是奇数6．（4分）在独立性检验中，统计量Χ2有两个临界值：3.841和6.635；当Χ2＞3.841时，有95%的把握说明两个事件有关，当Χ2＞6.635时，有99%的把握说明两个事件有关，当Χ2≤3.841时，认为两个事件无关．调查者通过询问50名男女大学生在选修课程时是否选择“统计学”课程，得到数据如下表：不选统计学选统计学男1310女720根据表中的数据，得到Χ2=≈4.844．根据这一数据分析，认为大学生的性别和是否选修“统计学”课程之间（）A．有95%的把握认为两者有关B．约有95%的选修“统计学”课程的学生是女性C．有99%的把握认为两者有关D．约有99%的选修“统计学”课程的学生是女性7．（4分）若定义运算：；，例如2?3=3，则下列等式不能成立的是（）A．a?b=b?a B．（a?b）?c=a?（b?c）C．（a?b）2=a2?b2D．c?（a?b）=（c?a）?（c?b）（c＞0）8．（4分）已知各项均为正数的数列{a n}满足a1=1，a n+2a n=39（n∈N*），那么数列{a n}的前50项和S50的最小值为（）A．637 B．559 C．481+25D．492+24二、填空题：本大题共6小题，每小题4分，共24分.9．（4分）在复平面内，复数i（1﹣i）对应的点的坐标是．10．（4分）观察下列等式：+i=cos+isin，（+i）2=cos+isin，（+i）3=cosπ+isiπ，（+i）4=cos+isin，…照此规律，可以推测对于任意的n∈N*，（+i）n=．11．（4分）在平面直角坐标系中，若向量=（x1，y1），=（x2，y2）且⊥，则x1x2+y1y2=0．把上述结论类比推广到空间：在空间直角坐标系中，若向量=（x1，y1，z1），=（x2，y2，z2），且⊥，则．12．（4分）已知+2=bi（a，b∈R，i为虚数单位），那么a+bi的共轭复数为．。

海淀区高一年级第二学期期中练习语文参考答案及评分标准2014.4一、本大题共6小题，每小题2分，共12分。

1.A2. A3. C4. D5. D6. C二、本大题共6分。

5.①无边落木萧萧下②申之以孝悌之义③同是天涯沦落人相逢何必曾相识④不积跬步无以至千里（本题共6分。

每空1分，有错则该空不得分）三、本大题共4分。

6. 评分要点：介绍的剧目内容正确，2分；具有宣传性、鼓动性1分；富有创意，1分。

四、本大题共5小题，共15分。

9. C（2分）（弊：使……衰败）10. C（2分）（A.然，○1代词，这样；○2形容词词尾，……的样子 B.而，○1连词，因而；○2连词，表修饰 C.则，连词，于是，就 D.○1……的原因；○2用来11. B（2分）（布衣、人臣、人君分别对应积善、积正、积德）12. 三代之废兴也//在其所积/积善多者/虽有一恶/是为过失/未足以亡/积恶多者/虽有一善/是为误中/未足以存/人君闻此//可以悚惧/ 布衣闻此//可以改容。

（本题5分。

“/”处为必断句处；“//”为可断可不断处。

每答对2处得1分。

答错2处扣1分，扣完5分为止）13．答案要点：积善才能够成就美名，积恶易招致自己身败名裂，恶行积累多了就无法掩盖，罪孽积累大了就不能化解了。

（本题4分。

每点1分。

意思对即可）五、本大题共2小题，共7分。

14．C（3分）（“飞蓬各自远”意思是诗人和友人分别后，各自像飘飞的蓬草般漂泊无依）15．评分要点：本题4分。

选择一个角度，举例正确，2分；结合相关诗句能分析出对“有别必怨”的突破即可给2分。

答案示例：示例1：“秋波落泗水，海色明徂徕”句，描绘了清澄的泗水秋波、明净的徂徕山色，诗中的山水形象，隽美秀丽，明媚动人，与诗人和友人之间纯洁无邪、真挚淳厚的友谊交相映衬，一扫送别诗“哀怨”之风。

（只分析出了对“有别必怨”的突破）示例2:“飞蓬各自远，且尽手中杯”句，写诗人想到各自将要远离，不禁举杯相劝的情形。

2013～2014学年度第二学期期中练习高 二 文 科 数 学（考试时间：100分钟 卷面总分：100分）一、选择题：本大题共10小题，每小题4分，共40分．在每小题给出的四个选项中，选出符合题目要求的一项.1. 已知集合},2,1{2m A =，},1{m B =，A B A = ，则=m （ ）A ．0或2B ．1或2C ．0或2D ．1或2 2.设复数z 满足z(2-3i)=6+4i （其中i 为虚数单位），则z 的模为（ ）A ．2B ．2C ．4D ．2i3.设集合{}0322≤-=x x x P ，3.02=m ，则下列关系中正确的是 （ ）A ．A m ⊂B ．A m ∉C ．{}A m ∉D ．{}A m ≠⊂4.已知集合{}R x x x A ∈≤=,2|,{|4,}B x x Z =≤∈,则A B ⋂=（ ）A ．(0,2)B ．[0,2]C ．{0,2}D ．{0,1,2}5.已知函数⎩⎨⎧≤>=0,40,log )(3x x x x f x ，则=)]9([f f （ ） A.16 B.23log C.1 D.48 6.已知命题:P x x R x lg 2,>-∈∃，命题:q ()f x 12--=x x x 不是奇函数 ,则（ ） A ．命题)()(q p ⌝⌝∨是假命题 B . 命题p q ∧是假命题C ．命题p q ∨是假命题D . 命题()p q ∧⌝是真命题7．已知函数xx f 21log )(=，若2|)(|≥x f ，则实数x 的取值范围是（ ）A ．410<<x 或4>x B ．41≤x 或4≥x C ．410≤<x 或4≥x D ．441≤<x 8.若1.01.1-=a π3log =b ，，341l o g =c ，则a 、b 、c 的大小关系为（ ） A ．c b a >> B ．c a b >> C ．b c a >> D ．a c b >>9.函数)]21(ln[x e y -=的图象可以看成是由函数ln(2)y x =-的图象（ ） A.向右平移12个单位长度，再向上移动1个单位长度得到的 B.向左平移12个单位长度，再向上移动1个单位长度得到的 C.向左平移1个单位长度，再向下移动1个单位长度得到的D.向右平移1个单位长度，再向上移动1个单位长度得到的10.已知函数)(2)()(2b a ab x b a x x f <+++-=的两个零点为)(,βαβα<，则实数βα,,,b a 的大小关系是（ ）A. βα<<<b aB.b a <<<βαC. b a <<<βαD.βα<<<b a第二部分（非选择题 共60分）二、填空题：本大题共7小题，每小题4分，共28分.11．已知i 为虚单位，则复数121-+i i 的对应的点在第 象限. 12.观察下列等式：13＋23＝（1＋2）2，13＋23＋33＝（1＋2＋3）2，13＋23＋33＋43＝（1＋2＋3＋4）2，…，根据上述规律，第．n 个等式．．．为. __________. 13. 函数)2(9.0log -=x y 的定义域 .14.函数||)(2x x x f --=的单调增区间是 .15．命题,0:≥∀x p 有1≥-x e ，写出命题p 的否定_______:； 命题p 为____命题（填真、假）16.已知函数⎪⎪⎩⎪⎪⎨⎧+=2141)(x x x f )40()4(<≤≥x x ，若关于x 的方程0)(=+m x f 仅有一个实根，则实数m 的取值范围是 .17.已知函数()f x 是定义在R 上的偶函数，且对任意的x ∈R ，都有(2)()f x f x +=.当01x ≤≤时，2()f x x =.若直线0=--k y x 与函数()y f x =的图象在[0,2]内恰有3个公共点，则实数k 的取值范围是 .三、解答题：本大题共3小题，共32分.解答应写出文字说明，演算步骤或证明过程.18设:p 实数x 满足26x x ≥+且042>+x x ，:q 实数x 满足03422<+-a ax x ，已知p 是q 的必要不充分条件，求a 的取值范围；19已知函数2)1(21)(-=x a x f ，1ln )(--=x x x g ，其中a ∈R . （Ⅰ）求函数)(x g 在1=x 处的切线方程；（Ⅱ）求)(x f )(x g -的单调区间；（Ⅲ）若)(x f )(x g -在[),1∞+上的最小值是0，求a 的取值范围.20已知函数xax x f 1)(-= （Ⅰ）若(]0,2x ∈， 求函数)(x f 的最大值.（Ⅱ）0<a 时，设函数xx x g 1ln )(--=，若()f x 与()g x 的图象在区间()21,e 上无交点，求实数a 的取值范围。

海淀区高一年级第二学期期中练习数 学参考答案及评分标准2014.4一、 选择题.二、填空题.9.410.12, 3-- 11. 1, 45-12. ①②③ 13. 5274,1614. 11123I 0)))43234（）或1 (II)(0,(,(, 说明：12题如果填写两个选项给2分，只填一个选项不给分； 其余两空题目都是每个空2分. 三、解答题15.解: ( I ) 2()cos 242f ππ=++= …………………….2分. ( II ) 因为22()sin 2sin cos cos cos2f x x x x x x =+++所以 ()1sin 2cos2f x x x =++ …………………….4分所以π())14f x x =++ …………………….6分所以()f x 的最小正周期为 2π2π=π||2T ϖ== …………………….8分 （Ⅲ）令πππ2π22π242k x k -≤+≤+ 所以3ππππ88k x k -≤≤+ 所以()f x 的单调递增区间为3πππ,π88k k k -+∈Z （）, …………………….10分16.解: ( I )解法一：设{}n a 的公差为d , 因为112n n a a n ++=+， 所以有1223112122a a a a ⎧+=+⎪⎪⎨⎪+=+⎪⎩ ，两式相减得到，21d =，即12d = ………………….2分 代入得到112a =………………….4分 所以11+1)222n na n =-⋅=（ ………………….6分解法二：设{}n a 的公差为d ,则1+1),n a a n d =-⋅（ 11+,n a a n d +=⋅ ………………….2分所以111221)22n n a a a n d dn a d ++=+-⋅=+-（ 所以有1122=2dn a d n +-+对*n ∈N 成立， 所以有12=112=2d a d ⎧⎪⎨-⎪⎩，解得11=21=2d a ⎧⎪⎪⎨⎪⎪⎩ ………………….4分 所以11+1)222n na n =-⋅=（ ………………….6分 (II) 因为1(),2n n a a S n +=所以(1)4n n nS += ………………….9分（Ⅲ）因为13,,m m a a a 成等比数列，所以213()=m m a a a ………………….10分即213422m m =⋅ ………………….11分 解得3,m =0m =(舍掉）所以3m = ………………….12分17. 解: ( I ) 由正弦定理sin sin a bA B=得到sin sin a B b A = ………………….2分 所以有sin cos a B a B = ………………….3分 所以sin cos B B =,即tan 1B = ………………….4分因为0,)B ∈π（, 所以π4B ∠= ………………….5分 （II ）在ACE ∆中，根据余弦定理222=2c o s C E A C A E A C A E C A E +-⋅∠ ………………….7分得到222π=424cos4CE +-⋅⋅（化简得CE ………………….8分 在ACE ∆中，sin sin ACE CAEAE CE∠∠= ………………….9分化简得到sin ACE ∠ ………………….10分因为π2ACE CAP ∠+∠=，所以cos sin 5CAP ACE ∠=∠=所以在Rt ACP ∆中，cos =5AC CAP AP ∠=代入得到AP = ……………….12分18解: (I) 3a 可能取的值 3,3,1,1-- ………………….2分 (II) 存在 ………………….3分这个数列的前6项可以为 1,2,1,212---，， （或者取1,23,210---，，，） ………………….5分 （Ⅲ）1210|...|a a a +++的最小值为1 ………………….6分 解法一：因为111,|||1|n n a a a +==+,所以n a ∈Z ，且所有的奇数项都为奇数，偶数项为偶数 因此1210,,...,a a a 中一定有5个奇数，5个偶数，所以1210|...|a a a +++一定是奇数，所以1210|...|1a a a +++≥令这10项分别为1,2,1,2121212----，，，，，，（或者为 1,2,3,210123----，，，，，，，或者为1234,3,21012----，，，，，，，） 则有1210|...|=1a a a +++ ………………….10分 解法二：因为111,|||1|n n a a a +==+,所以n a ∈Z ，且所有的奇数项都为奇数，偶数项为偶数 又因为221()(1)n n a a +=+ 所以221()()12n n n a a a +--= 所以有2211101012a a a --= 22109912a a a --= ......2232212a a a --= 2221112a a a --=把上面的10个式子相加，得到221111210102(...)a a a a a --=+++ 所以有21210111|...||11|2a a a a +++=- 因为离11最近的奇数的平方是 9，所以有12101|...||911|=12a a a +++≥- 令这10项分别为1,2,1,2121212----，，，，，，（或者为 1,2,3,210123----，，，，，，，或者为1234,3,21012----，，，，，，，） 则有1210|...|=1a a a +++ ………………….10分说明：解答题有其它正确解法的请酌情给分.。

海淀区高一年级第二学期期中练习数 学参考答案及评分标准 2014.4一、 选择题.二、填空题.10.12, 3-- 11. 1, 45- 12. ①②③ 13. 5274,1614. 11123I 0)))43234（）或1 (II)(0,(,(,说明：12题如果填写两个选项给2分，只填一个选项不给分； 其余两空题目都是每个空2分. 三、解答题15.解: ( I ) 2()cos 24222f ππ=++= …………………….2分. ( II ) 因为22()sin 2sin cos cos cos2f x x x x x x =+++所以 ()1sin 2cos2f x x x =++ …………………….4分所以π())14f x x =++ …………………….6分所以()f x 的最小正周期为 2π2π=π||2T ϖ== …………………….8分 （Ⅲ）令πππ2π22π242k x k -≤+≤+ 所以3ππππ88k x k -≤≤+ 所以()f x 的单调递增区间为3πππ,π88k k k -+∈Z （）, …………………….10分16.解: ( I )解法一：设{}n a 的公差为d , 因为112n n a a n ++=+， 所以有1223112122a a a a ⎧+=+⎪⎪⎨⎪+=+⎪⎩ ，两式相减得到，21d =，即12d = ………………….2分 代入得到112a =………………….4分 所以11+1)222n na n =-⋅=（ ………………….6分解法二：设{}n a 的公差为d ,则1+1),n a a n d =-⋅（ 11+,n a a n d +=⋅ ………………….2分所以111221)22n n a a a n d dn a d ++=+-⋅=+-（ 所以有1122=2dn a d n +-+对*n ∈N 成立， 所以有12=112=2d a d ⎧⎪⎨-⎪⎩，解得11=21=2d a ⎧⎪⎪⎨⎪⎪⎩ ………………….4分 所以11+1)222n na n =-⋅=（ ………………….6分 (II) 因为1(),2n n a a S n += 所以(1)4n n nS += ………………….9分（Ⅲ）因为13,,m m a a a 成等比数列，所以213()=m m a a a ………………….10分即213422m m=⋅………………….11分 解得3,m =0m =(舍掉）所以3m = ………………….12分17. 解: ( I ) 由正弦定理sin sin a bA B=得到sin sin a B b A = ………………….2分 所以有sin cos a B a B = ………………….3分 所以sin cos B B =,即tan 1B = ………………….4分因为0,)B ∈π（, 所以π4B ∠= ………………….5分 （II ）在ACE ∆中，根据余弦定理222=2cos CE AC AE AC AE CAE +-⋅∠ ………………….7分得到222π=424cos4CE +-⋅⋅（化简得CE ………………….8分 在ACE ∆中，sin sin ACE CAEAE CE∠∠= ………………….9分化简得到sin =5ACE ∠ ………………….10分因为π2ACE CAP ∠+∠=，所以cos sin 5CAP ACE ∠=∠=所以在Rt ACP ∆中，cos AC CAP AP ∠=代入得到AP = ……………….12分18解: (I) 3a 可能取的值 3,3,1,1-- ………………….2分 (II) 存在 ………………….3分这个数列的前6项可以为 1,2,1,212---，， （或者取1,23,210---，，，） ………………….5分 （Ⅲ）1210|...|a a a +++的最小值为1 ………………….6分 解法一：因为111,|||1|n n a a a +==+,所以n a ∈Z ，且所有的奇数项都为奇数，偶数项为偶数 因此1210,,...,a a a 中一定有5个奇数，5个偶数，所以1210|...|a a a +++一定是奇数，所以1210|...|1a a a +++≥令这10项分别为1,2,1,2121212----，，，，，，（或者为 1,2,3,2101234----，，，，，，，或者为1234,3,21012----，，，，，，，） 则有1210|...|=1a a a +++ ………………….10分 解法二：因为111,|||1|n n a a a +==+,所以n a ∈Z ，且所有的奇数项都为奇数，偶数项为偶数 又因为221()(1)n n a a +=+ 所以221()()12n n n a a a +--= 所以有2211101012a a a --= 22109912a a a --= ......2232212a a a --= 2221112a a a --=把上面的10个式子相加，得到221111210102(...)a a a a a --=+++ 所以有21210111|...||11|2a a a a +++=- 因为离11最近的奇数的平方是 9，所以有12101|...||911|=12a a a +++≥- 令这10项分别为1,2,1,2121212----，，，，，，（或者为 1,2,3,2101234----，，，，，，，或者为1234,3,21012----，，，，，，，） 则有1210|...|=1a a a +++ ………………….10分说明：解答题有其它正确解法的请酌情给分.。

北京市海淀区2012-2013学年高二数学下学期期中试题文（扫描版）海淀区高二年级第二学期期中练习数学（文科）参考答案及评分标准 2013.4一、选择题：本大题共8小题，每小题4分，共32分.1．C 2．D 3．C 4．C 5．A 6．D 7．C 8．D二、填空题：本大题共6小题，每小题4分，共24分.9． 11710．2 11．① 12．1a ≥ 13．0 14．()31327x f x x =+； ()3132n n nx f x x =-+ (每空2分)三、解答题：本大题共4小题，共44分. 15.解：2'()32f x x ax b =-+ …………………………..2分.()f x 在0x =处取得极大值1(0)1'(0)0f f =⎧∴⎨=⎩，所以1,0c b == …………………………..5分 2'()32(32)f x x ax x x a ∴=-=-令'()0f x =得203或a x x == …………………………..6分 ①若0a >，则()f x 和'()f x 情况如下：②若0a <，则()f x 和'()f x 情况如下：分 综上讨论可得0a >满足题意.16.解：（I ）12(3)2n n n x x x n --+=≥ .....................................2分 （II ）10x =，22x =，3211()12x x x =+=，43213()22x x x =+= 1212a x x ∴=-=，2321a x x =-=-，34312a x x =-= ………………4分 推测12(2)n n a -=- (6)分证明：对于任意*n N ∈，1n n n a x x +=- 121111111()()222n n n n n n n n n a x x x x x x x a ++++++=-=+-=--=-………………………….9分{}n a ∴是以2为首项，以12-为公比的等比数列. 故11122()2(2)n n n a --=⋅-=- ………………10分17.（I ） //CD 截面EFGH 且CD ⊂平面ADC ，平面ADC 截面EFGH GF =∴ //GF CD ………………………2分 同理可证//AB GH ………………………3分 （II ）DC BD ⊥，//GF CD GF BD ∴⊥ ………………………4分AD ⊥截面EFGH ，AD GF ∴⊥ ………………………5分又BD AD D = GF ∴⊥平面ABD ……………………….7分 （III ） 由（I ）知//GF CD ，//AB GH同（I ）的证明方法可得，//AB EF ，//HE CD∴//GH EF ，//HE GF∴ EFGH 是平行四边形 ……………………….8分 又GF ⊥平面ABD ，GF GH ∴⊥∴ EFGH 是矩形 …………………………9分在ABD ∆中，GH GD AB AD=，∴GH GD x == 在ACD ∆中，GF AG DC AD =，∴22x GF -= ∴2=2矩形EFGH x S GH GF x -⋅=⋅ AD ⊥平面EFGH ∴GD 是四棱锥D EFGH -的高∴ 四棱锥D EFGH -的体积 ()V x 32121(2)3326矩形EFGH x x GD S x x x -=⋅=⋅⋅=-+，(0,2)x ∈ ……………..10分 则21'()(34)6V x x x =-+ 令'()0V x =得0x =（舍）43或x =………………………11分 当403x <<时，'()0V x >，()V x 在4(0,)3上单调递增； 当423x <<时，'()0V x <，()V x 在4(,2)3上单调递减， ∴max 41641616()()(2)3627981V x V ==-+⨯= …………………….12分 18.解：22'()(2)()(22)x x x f x x k e x kx k e x kx x k e =++++=+++……………....2分整理得'()()(2)xf x x k x e =++ ……………………………..3分（1）若函数()f x 在(0,1)上单调递减，则在(0,1)x ∈上'()0f x ≤，由于0x e >∴当(0,1)x ∈时，有()(2)0x k x ++≤由二次函数()(2)y x k x =++的图像可知，1k -≥，即1k ≤-时满足题意………5分（2）若2k >，有2k -<-，则当(,)x k ∈-∞-时，()(2)0x k x ++>，'()0f x >，函数()f x 单调递增； 当(,2)x k ∈--时，()(2)0x k x ++<，'()0f x <，函数()f x 单调递减；当(2,)x ∈-+∞时，()(2)0x k x ++>，'()0f x >，函数()f x 单调递增；………………………………8分 若2k =，则2'()(2)0x f x x e =+≥，且仅当2x =-时'()0f x =，所以函数()f x 单调递增； ..…………………………9分 若2k <，有2k ->-，则当(,2)x ∈-∞-时，()(2)0x k x ++>，'()0f x >，函数()f x 单调递增； 当(2,)x k ∈--时，()(2)0x k x ++<，'()0f x <，函数()f x 单调递减；当(,)x k ∈-+∞时，()(2)0x k x ++>，'()0f x >，函数()f x 单调递增；………………………..12分综上，当2k >时，函数()f x 的单调递增区间是(,)k -∞-和(2,)-+∞，单调递减区间是(,2)k --；当2k =时，函数()f x 的单调递增区间是(,)-∞+∞，无单调递减区间；当2k <时，函数()f x 的单调递增区间是(,2)-∞-和(,)k -+∞，单调递减区间是(2,)k --.。

北京101中学2013－2014学年下学期高二年级期中考试数学试卷（文科）一、选择题：本大题单选 共8小题，每小题5分，共40分.1. 已知命题p ：x ∀∈R ，210x x +->；命题q ：x ∃∈R ，sin cos x x +=则下列判断正确的是（ ）A. p ⌝是假命题B. q 是假命题C. p q ∨⌝是真命题D. ()p q ⌝∧是真命题 2. 若集合{}23M x x =-<<，{}121x N x +=≥，则MN =（ ）A. (3,)+∞B. (1,3)-C. [1,3)-D. (2,1]-- 3. 已知函数2()f x x bx c =++，则“0c <”是“0x ∃∈R ，使0()0f x <”的（ ） A. 充分而不必要条件 B . 必要而不充分条件 C . 充分必要条件D . 既不充分也不必要条件4. 函数()f x = （ ）A. 在ππ(,)22-上递增 B . 在π(,0]2-上递增，在π(0,)2上递减 C. 在ππ(,)22-上递减 D . 在π(,0]2-上递减，在π(0,)2上递增 5. 已知定义在R 上的函数()f x 的对称轴为3x =-，且当3x ≥-时，()23xf x =-.若函数()f x 在区间(1,)k k -（k ∈Z ）上有零点，则k 的值为 （ ）A. 2或7-B. 2或8-C. 1或7-D. 1或8-6. 函数2sin()y x ωϕ=+在一个周期内的图象如图所示，则此函数的解析式可能是（ ）A. 2sin(2)4y x π=-B. 2sin(2)4y x π=+C. 32sin()8y x π=+D. 72sin()216x y π=+7. 如果函数()=y f x 图象上任意一点的坐标(,)x y 都满足方程 lg()lg lg x y x y +=+，那么正确的选项是 （ ）A. ()=y f x 是区间（0，+∞）上的减函数，且x y +4≤B. ()=y f x 是区间（1，+∞）上的增函数，且x y +4≥C. ()=y f x 是区间（1，+∞）上的减函数，且x y +4≥D. ()=y f x 是区间（1，+∞）上的减函数，且x y +4≤8. 若直角坐标平面内的两点,P Q 满足条件：①,P Q 都在函数()=y f x 的图象上；②,P Q 关于原点对称，则称点对[,P Q ]是函数()=y f x 的一对“友好点对”（注：点对[,P Q ]与[,Q P ]看作同一对“友好点对”）。

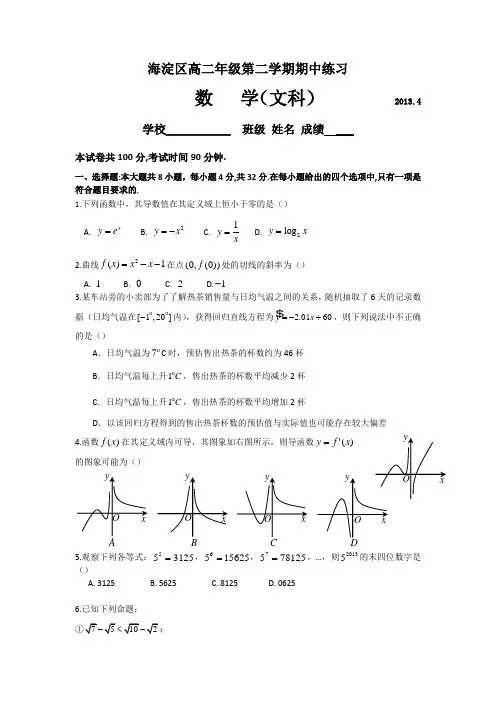
海淀区高二年级第二学期期中练习数 学（文科） 2013.4学校___________ 班级 姓名 成绩 ___本试卷共100分,考试时间90分钟.一、选择题:本大题共8小题，每小题4分,共32分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.下列函数中，其导数值在其定义域上恒小于零的是（）A. x y e =B. 2y x =- C. 1y x=D. 2log y x = 2.曲线1)(2--=x x x f 在点))0(,0(f 处的切线的斜率为（）A. 1B. 0C. 2D.1-3.某车站旁的小卖部为了了解热茶销售量与日均气温之间的关系，随机抽取了6天的记录数据（日均气温在[1,20]- 内），获得回归直线方程为 2.0160y x =-+，则下列说法中不正确的是（）A ．日均气温为7 C 时，预估售出热茶的杯数约为46杯B ．日均气温每上升1C ，售出热茶的杯数平均减少2杯 C ．日均气温每上升1C ，售出热茶的杯数平均增加2杯D ．以该回归方程得到的售出热茶杯数的预估值与实际值也可能存在较大偏差 4.函数)(x f 在其定义域内可导，其图象如右图所示，则导函数的图象可能为（）5.观察下列各等式：312555=，1562556=，7812557=，…，则20135的末四位数字是（）A. 3125B. 5625C. 8125D. 06256.已知下列命题： ；②三角形ABC 的三个内角满足sin sin sin A B C +>； ③存在等比数列{}n a 满足1322a a a +=成立.其中所有正确命题的序号是（） A.①B.①②C.②③D. ①②③7.若水以恒速（即单位时间内注入的体积相同）注入右图的容器，则容器中水的高度h 与时间t 的函数关系的图象是（）8.若函数b ax x x f ++=3)(有三个零点，分别为123,,x x x ,且满足11<x ,12=x ,13>x ，则实数a 的取值范围是（）A ．(,0)-∞B ．(,1)-∞-C ．(,2)-∞-D ．(,3)-∞- 二、填空题:本大题共6小题,每小题4分,共24分.把答案填在题中横线上.9.某路口的红绿灯设定如下：红灯的时间为40秒,黄灯的时间为5秒,绿灯的时间为40秒.假如你到达路口的时刻是随机的，则当你到达路口恰逢黄灯的概率是_________. 10.曲线32()f x x x =-过点．．（1,0）的切线有__________条. 11.右图是依据1981～2001年我国出口贸易量E x （亿美元）的原始数据画的散点图.给出下列经验公式：①y ax b =+②2y ax b =+③bx e a y ⋅=请依据该散点图的特征，指出拟合程度最．不好．．的经验公式的序号：__________.12.函数sin y ax x =-是单调递增函数，则实数a 的取值范围_____________.13.函数ln xy x=在点x e =处的瞬时变化率为__________. 14.已知函数()3x f x x =+,构造如下函数序列()n f x :()()1[]n n f x f f x -=（*∈N n ，且2≥n ）, 其中()1()f x f x =，()0>x ，则3()f x =_______________，函数()n f x =_______________.三、解答题:本大题共4小题,共44分.解答应写出文字说明,证明过程或演算步骤. 15. (本小题共10分)已知函数32()f x x ax bx c =-++在0x =处取得极大值．．．1.求实数b ,c 的值和实数a 的取值范围.16.（本小题共10分）已知点列A n (x n,0)，n ∈N *，其中x 1＝0，x 2＝2，A 3是线段A 1A 2的中点，A 4是线段A 2A 3的中点，…，A n 是线段A n －2A n －1的中点，…， （I ）写出x n 与x n －1、x n －2之间的关系式(n ≥3)；（II ）设a n ＝x n ＋1－x n ，计算a 1，a 2，a 3，由此推测数列{a n }的通项公式，并加以证明．17.(本小题共12分)已知四面体ABCD 中，DC BD ⊥，22AB AD DC ===.AD ⊥平面EFGH ，且//AB 截面EFGH ，//CD 截面EFGH . （I ）求证：//GF CD ，//AB GH ； （II ）求证：GF ⊥平面ABD ； （III ）设GD x =，求四棱锥D EFGH -的体积()V x 的最大值.18.（本小题共12分）已知函数2()()xf x x kx k e =++，（I ）若函数()f x 在区间(0,1)上单调递减，求实数k 的取值范围； （II ）求函数()f x 的单调区间.BD海淀区高二年级第二学期期中练习数学（文科）参考答案及评分标准 2013.4一、选择题：本大题共8小题，每小题4分，共32分.1．C 2．D 3．C 4．C 5．A 6．D 7．C 8．D二、填空题：本大题共6小题，每小题4分，共24分.9． 11710．2 11．① 12．1a ≥13．0 14．()31327xf x x =+； ()3132n nnx f x x =-+ (每空2分)三、解答题：本大题共4小题，共44分.15.解：2'()32f x x ax b =-+ …………………………..2分.()f x 在0x =处取得极大值1(0)1'(0)0f f =⎧∴⎨=⎩，所以1,0c b == …………………………..5分 2'()32(32)f x x ax x x a ∴=-=-令'()0f x =得203或ax x == …………………………..6分①若0a >，则()f x 和'()f x 情况如下：②若0a <，则()f x 和'()f x 情况如下：综上讨论可得0a >满足题意.16.解：（I ）12(3)2n n n x x x n --+=≥ .....................................2分 （II ）10x =，22x =，3211()12x x x =+=，43213()22x x x =+=1212a x x ∴=-=，2321a x x =-=-，34312a x x =-= ………………4分推测12(2)n n a -=-….….……….………………6分证明：对于任意*n N ∈，1n n n a x x +=-121111111()()222n n n n n n n n n a x x x x x x x a ++++++=-=+-=--=-………………………….9分{}n a ∴是以2为首项，以12-为公比的等比数列.故11122()2(2)n n n a --=⋅-=-………………10分17.（I ） //CD 截面EFGH 且CD ⊂平面ADC ，平面ADC 截面EFGH GF =∴ //GF CD ………………………2分同理可证//AB GH ………………………3分（II ） DC BD ⊥，//GF CD GF BD ∴⊥ ………………………4分AD ⊥ 截面EFGH ，AD GF ∴⊥ ………………………5分 又BD AD D = GF ∴⊥平面ABD ……………………….7分 （III ） 由（I ）知//GF CD ，//AB GH同（I ）的证明方法可得，//AB EF ，//HE CD ∴//GH EF ，//HE GF∴ EFGH 是平行四边形 ……………………….8分 又GF ⊥ 平面ABD ，GF GH ∴⊥∴ EFGH 是矩形 …………………………9分在ABD ∆中，GH GDAB AD =，∴GH GD x == 在ACD ∆中，GF AG DC AD =，∴22xGF -= ∴2=2矩形EFGH xS GH GF x -⋅=⋅ AD ⊥平面EFGH ∴GD 是四棱锥D EFGH -的高 ∴ 四棱锥D EFGH -的体积()V x 32121(2)3326矩形EFGH x x GD S x x x -=⋅=⋅⋅=-+，(0,2)x ∈ ……………..10分则21'()(34)6V x x x =-+令'()0V x =得0x =（舍）43或x =………………………11分 当403x <<时，'()0V x >，()V x 在4(0,)3上单调递增；当423x <<时，'()0V x <，()V x 在4(,2)3上单调递减，∴max 41641616()()(2)3627981V x V ==-+⨯= …………………….12分18.解：22'()(2)()(22)x x xf x x k e x kx k e x kx x k e =++++=+++……………....2分整理得'()()(2)xf x x k x e =++ ……………………………..3分（1）若函数()f x 在(0,1)上单调递减，则在(0,1)x ∈上'()0f x ≤， 由于0x e >∴当(0,1)x ∈时，有()(2)0x k x ++≤由二次函数()(2)y x k x =++的图像可知，1k -≥，即1k ≤-时满足题意………5分 （2）若2k >，有2k -<-，则当(,)x k ∈-∞-时，()(2)0x k x ++>，'()0f x >，函数()f x 单调递增； 当(,2)x k ∈--时，()(2)0x k x ++<，'()0f x <，函数()f x 单调递减； 当(2,)x ∈-+∞时，()(2)0x k x ++>，'()0f x >，函数()f x 单调递增； ………………………………8分 若2k =，则2'()(2)0x f x x e =+≥，且仅当2x =-时'()0f x =，所以函数()f x 单调递增； ..…………………………9分 若2k <，有2k ->-，则当(,2)x ∈-∞-时，()(2)0x k x ++>，'()0f x >，函数()f x 单调递增； 当(2,)x k ∈--时，()(2)0x k x ++<，'()0f x <，函数()f x 单调递减； 当(,)x k ∈-+∞时，()(2)0x k x ++>，'()0f x >，函数()f x 单调递增； ………………………..12分 综上，当2k >时，函数()f x 的单调递增区间是(,)k -∞-和(2,)-+∞，单调递减区间是(,2)k --；当2k =时，函数()f x 的单调递增区间是(,)-∞+∞，无单调递减区间；当2k <时，函数()f x 的单调递增区间是(,2)-∞-和(,)k -+∞，单调递减区间是(2,)k --.。

海淀区九年级第二学期期末测评数学试卷答案及评分参考2014．6 一、选择题（本题共32分，每小题4分）二、填空题（本题共16分，每小题4分）三、解答题（本题共30分，每小题5分）13. 解：011||π12cos302--++-（）（）122=-+-…………………………………………………………4分=1. …………………………………………………………………………………5分14.323 1.x yx y+=⎧⎨-=⎩，①②解：由①3⨯+②得, 510x=.解得, 2x=. …………………………………………………………………………2分把2x=代入①得，1y=. ……………………………………………………………4分∴原方程组的解为2,1.xy=⎧⎨=⎩……….……………………………………………………5分15.证明：在△CAE和△DBE中，,,,C DCEA DEBEAEB∠=∠⎧⎪∠=∠⎨⎪=⎩∴△CAE≌△DBE．……………………………………………………………………3分∴CE=DE．……………………………………………………………………………4分∵EA= EB,∴CE+EB=DE+EA．即BC=AD. ……………………………………………………5分16. 解：∵22440,a ab b-+=2(2)0.a b-=∴………………………………………………………………………1分A2.a b =∴ ……………………………………………………………………………2分∵0ab ≠， ∴2222()()()()a b a ba b a b a b a b a b ++⋅-=⋅---+2a ba b+=+ ………………………………………………………3分 222b bb b+=+ ………………………………………………………4分 4.3= ……………………………………………………………5分 17. 解：设这份快餐含有x 克的蛋白质. ……………………………………………………1分 根据题意可得:440070%x x +≤⨯，……………………………………………3分 解不等式，得56.x ≤ …………………………………………………………4分 答：这份快餐最多含有56克的蛋白质. …………………………………………5分18．解：（1）A (1)m ,在4y x=的图象上，∴441m ==． …………………………………………………………………………1分 ∴A 点的坐标为(14),.∵A 点在一次函数2+=kx y 的图象上，4 2 .k =+∴ 2 .k =∴2 2.y x =+∴一次函数的解析式为 …………………………………………………2分令0,y =即220x +=，解得1x =-．∴点B 的坐标为（-1,0）． ………………………………………………………3分 （2）点P 的坐标为（2，2）；点C 的坐标为（3，0）. ………………………………5分 四、解答题（本题共20分，每小题5分）19．（1）证明：∵点D 、E 分别是边BC 、AC 的中点，∴DE ∥AB . ……………………………………………………………………1分 ∵AF ∥BC ,∴四边形ABDF 是平行四边形. ………………………………………………2分（2）解：过点F 作FG ⊥AC 于G 点. ∵BC=4，点D 是边BC 的中点，∴BD=2.由（1）可知四边形ABDF 是平行四边形， ∴AF =BD=2. ∵∠CAF =45°，∴AG =. …………………………………………………………………3分在Rt △FGC 中，∠FGC =90°,，∴=…………………………………………………4分 ∴AC =AG+GC=113.22CAFSAC FG =⋅=⨯= ……………………………………5分 20． 解：（1）二；……………………………………………………………………………1分（2）……………………………………3分（3）三；77. ………………………………………………………………………5分21． 证明：（1）连接OC .∵OA OC =,∴1 2.∠=∠.又∵312,∠=∠+∠∴32 1.∠=∠ 又∵421∠=∠，∴4 3.∠=∠ ……………………1分 ∴OC ∥DB . ∵CE ⊥DB ，∴OC ⊥CF .又∵OC 为⊙O 的半径，∴CF 为⊙O 的切线． ………………………………………………………2分 （2）连结AD .在Rt △BEF 中，∠BEF =90°, BF =5,3sin 5F =，∴3BE =. ……………………………………………………………………3分 ∵OC ∥BE ,∴FBE △∽FOC △.∴.FB BEFO OC= 设⊙O 的半径为r ,∴53.5r r=+A∴152r =. ……………………………………………………………………4分 ∵AB 为⊙O 直径， ∴15AB =. ∴90ADB ∠=. ∵4EBF ∠=∠, ∴F BAD ∠=∠. ∴3sin sin .5BD BAD F AB ∠=== ∴3.155BD = ∴9BD =．……………………………………………………………………5分22． 解：（1； …………………………………………………………………1分……………………………………………………………2分（2）…………………4分最大三角形的斜边长分别是2a ,2a ．………………………………………………………5分 五、解答题（本题共22分，第23题7分，第24题7分，第25题8分） 23． 解：（1）222(1)421(1)m m m m m ∆=-+=++=+，……………………………1分由0m >知必有10m +>，故0∆>.∴方程①总有两个不相等的实数根. ……………………………………………2分 （2）令10y =，依题意可解得(1,0)A -，(,0)B m .∵平移后，点A 落在点'(1,3)A 处，∴平移方式是将点A 向右平移2个单位，再向上平移3个单位得到. ∴点(,0)B m 按相同的方式平移后，点'B 为(2,3)m +. ……………………3分 则依题意有2(2)(9)(2)2(1)3m m m m +--+++=. …………………………4分 解得13m =，252m =-（舍负）. ∴m 的值为3. ………………………………………………………………………5分（3）32k =. ………………………………………………………………………7分24.解:（1）…………………………………………………2分（2）连接BF .∵将ABD △沿射线BC 方向平移，得到FCE △，∴AD ∥EF , AD =EF ；AB ∥FC , AB =FC .∵∠ABC=90°，∴四边形ABCF 为矩形.∴AC =BF . ……………………………………3分∵AD BE ⊥,∴EF BE ⊥. …………………………………4分∵AD a =，AC b =，∴EF a =，BF b =.∴BE =. ………………………………………………………………5分（3）180α︒-； α . ……………………………………………………………7分25. 解：（1）①P 2，P 3； ……………………………………………………………………2分②P （-4，6）或P （4，-2）. …………………………………………………4分 （2）①解:∵⊙P 同时为正方形ABCD 与正方形EFGH 的“等距圆”，∴⊙P 同时过正方形ABCD 的对称中心E 和正方形EFGH 的对称中心I . ∴点P 在线段EI 的中垂线上.∵A （2，4），正方形ABCD 的边CD 在x 轴上；F （6，2），正方形EFGH 的边HE 在y 轴上，∴E （0，2），I （3，5）∴∠I EH=45°，设线段EI 的中垂线与y 轴交于点L ，与x 轴交于点M ，∴△LIE 为等腰直角三角形，LI ⊥y 轴，∴L （0，5），∴△LOM 为等腰直角三角形，LO=OM∴M （5，0），∴P 在直线y=-x +5上，∴设P （p ，-p +5）过P 作PQ ⊥直线BC 于Q ，连结PE ，∵⊙P 与BC 所在直线相切，∴PE=PQ ，∴()()222522p p p +-+-=+，解得：15p =+，25p =-∴．12(5(5P P +--．.……………………………………5分 ∵⊙P 过点E ，且E 点在y 轴上，--=--．…6分∴⊙P在y轴上截得的弦长为22242=44②0r r<<>+…………………………………………………8分注：其他解法请参照给分.。

2012-2013学年北京市海淀区高二（下）期中数学试卷（理科）一、选择题：本大题共8小题，每小题4分，共32分.在每小题给出的四个选项中，只有一项是符合题目要求的.1. 已知向量a →=(1, x, −2)，b →=(2, 1, x)，且a →⊥b →，则x 的值为（ ） A.−1 B.0 C.1 D.22. 曲线f(x)=1x 在点（1, f(1)）处的切线的倾斜角为（ ）A.π4 B.π3C.2π3D.3π43. 函数f(x)在其定义域内可导，其图象如图所示，则导函数y =f′(x)的图象可能为（ ）A. B.C. D.4. 观察下列各等式：55=3125，56=15625，57=78125，…，则52013的末四位数字是（ ） A.3125 B.5625C.8125D.06255. 已知下列命题： ①√7−√5<√10−√2；②三角形ABC 的三个内角满足sin A +sin B >sin C ； ③存在等比数列{a n }满足a 1+a 3=2a 2成立． 其中所有正确命题的序号是（ ） A.① B.①②C.②③D.①②③6. 若水以恒速（即单位时间内注入的体积相同）注入图的容器，则容器中水的高度ℎ与时间t 的函数关系的图象是（ ）A. B.C. D.7. 若函数f(x)=x 3+ax +b 有三个零点，分别为x 1，x 2，x 3，且满足x 1<1，x 2=1，x 3>1，则实数a 的取值范围是（ ）A.(−∞, 0)B.(−∞, −1)C.(−∞, −2)D.(−∞, −3)8. 已知正方体ABCD −A 1B 1C 1D 1的棱长为1，P 是截面A 1BD 内（包括边界）的动点，则C 1P →⋅C 1B →的值不可能是（ ） A.0.9 B.1.2C.1.5D.1.8二、填空题：本大题共6小题，每小题4分，共24分.把答案填在题中横线上.已知三个点A(1, −1, b)，B(2, a, 1)，O(0, 0, 0)在同一条直线上，则a =________，b =________．函数y =ax −sin x 是单调递增函数，则实数a 的取值范围________．由曲线y=x2，y=2x围成的封闭图形的面积为________．如图所示，已知三棱柱A′B′C′−ABC的侧棱垂直于底面，AC⊥CB，且AC=CB=CC′=2．若点E为A′B′中点，则CE与底面ABC所成角的余弦值为________．若函数f(x)=(x2−3)e x，给出下面四个结论：①f(−3)是f(x)的极大值，f(1)是f(x)的极小值；②f(x)<0的解集为{x|−√3<x<√3}；③f(x)没有最小值，也没有最大值；④f(x)有最小值，没有最大值，其中正确结论的序号有________．已知函数f(x)=xx+3，构造如下函数序列f n(x)：f n(x)=f[f n−1(x)](x∈N∗，且n≥2)，其中f1(x)=f(x)，(x>0)，则f3(x)=________，函数f n(x)的值域为________．三、解答题：本大题共4小题，共44分.解答应写出文字说明，证明过程或演算步骤.已知函数f(x)=a23x3−2ax2+bx其中a，b∈R，且曲线y=f(x)在点（0, f(0)）处的切线斜率为3．（1）求b的值；（2）若函数f(x)在x=1处取得极大值，求a的值．已知点的序列A n(x n, 0)，n∈N∗，其中x l=0，x2=a(a>0)，A3是线段A l A2的中点，A4是线段A2A3的中点，…，A n是线段A n−2A n−1的中点，…．（1）写出x n与x n−1、x n−2之间的关系式(n≥3)；（2）设a n=x n+1−x n，计算a l，a2，a3，由此推测数列{a n}的通项公式，并加以证明．已知平面ADEF⊥平面ABCD，其中ADEF为矩形，AB // CD，AB⊥AD，且AB=2CD=2DE=4，AD=2√2，如图所示．（1）求证：BE⊥AC；（2）求二面角B−CE−D的余弦值；（3）在线段AF上是否存在点P，使得BP // 平面ACE，若存在，确定点P的位置，若不存在，请说明理由．已知函数f(x)=ax2−(a+2)x+ln x．（1）当a=−2时，判断函数f(x)零点的个数；（2）求函数f(x)的单调区间．参考答案与试题解析2012-2013学年北京市海淀区高二（下）期中数学试卷（理科）一、选择题：本大题共8小题，每小题4分，共32分.在每小题给出的四个选项中，只有一项是符合题目要求的. 1.【答案】 D【考点】向量的数量积判断向量的共线与垂直 【解析】根据向量的数量积与垂直之间的关系建立方程，利用方程解x 即可． 【解答】解：因为向量a →=(1, x, −2)，b →=(2, 1, x)，且a →⊥b →， 所以a →⋅b →=0，即(1, x, −2)⋅(2, 1, x)=2+x −2x =0， 解得x =2． 故选D ． 2.【答案】 D【考点】利用导数研究曲线上某点切线方程 直线的倾斜角【解析】求出函数的导数，利用导数的几何意义求切线的斜率，进而利用斜率和倾斜角之间的关系求切线的倾斜角． 【解答】解：因为f(x)=1x ，所以f′(x)=−1x 2，所以函数在点（1, f(1)）处的切线斜率k =f ′(1)=−1， 由k =tan α=−1，解得α=3π4，即切线的倾斜角为3π4．故选D ． 3.【答案】 C【考点】函数的图象变换 【解析】根据函数的单调性确定f ′(x)的符号即可． 【解答】解：由函数f(x)的图象可知，函数在自变量逐渐增大的过程中，函数先递增，然后递减，再递增，当x >0时，函数单调递增，所以导数f ′(x)的符号是正，负，正，正．对应的图象为C ． 故选C ． 4.【答案】 A【考点】进行简单的合情推理 【解析】由上述的几个例子可以看出末四位数字的变化，3125，5625，8125，0625即末四位的数字是以4为周期的变化的，故2013除以4余1，即末四位数为3125． 【解答】解：55=3125的末四位数字为3125，56=15625的末四位数字为5625，57=78125的末四位数字为8125，58=390625的末四位数字为0625，59=1953125的末四位数字为3125…， 根据末四位数字的变化，3125，5625，8125，0625即末四位的数字是以4为周期的变化的， 故2013除以4余1，即末四位数为3125．则52013的末四位数字为3125． 故选A ． 5.【答案】 D【考点】命题的真假判断与应用 【解析】①利用平方法进行判断大小．②利用诱导公式和两角和的正弦公式判断．③利用等比数列的通项公式，举常数数列即可． 【解答】解：①因为√7−√5>0，√10−√2>0，所以(√7−√5)2=12−2√35，(√10−√2)2=12−2√20，所以√7−√5<√10−√2，所以①正确．②因为sin C =sin (π−A −B)=sin (A +B)=sin A cos B +cos A sin B <sin A +sin B ，所以②正确． ③若数列{a n }为非零的常数列，比如a n =1，则满足a 1+a 3=2a 2成立，所以③正确． 故选D ． 6.【答案】 C【考点】进行简单的合情推理 【解析】考查容器的形状来确定其高度的变化规律，选择图形即可． 【解答】解：此容器从下往上口径先由小、变大，再由大变小， 故等速注入液体其高度增加先是越来越慢，再变快， 只有C 满足条件， 故选C ．7.【答案】 D【考点】函数的零点与方程根的关系 【解析】利用函数零点的取值可以判断， 【解答】解：因为x 2=1，所以f(1)=a +b =0，即b =−a ， 所以f(x)=x 3+ax +b =x 3+ax +−a ．函数导数为f ′(x)=3x 2+a ，因为f(x)=x 3+ax +b 有三个零点，所以f ′(x)=0，有两个不等的实根，所以a <0．则由f ′(x)=0得x =±√−a3．即当x =−√−a3函数取得极大值，当x =√−a3时，函数取得极小值． 因为x 1<1，x 3>1， 所以√−a3>1，解得a <−3． 故选D ． 8.【答案】 A【考点】平面向量数量积的运算 【解析】将P 点在截面A 1BD 内（包括边界）运动，结合正方体的性质加以观察可得：当P 与点B 重合时C 1P →⋅C 1B →达到最大值；当P 点与D 点或A 1点重合时，C 1P →⋅C 1B →达到最小值．再由题中的数据加以计算，可得积C 1P →⋅C 1B →的范围为[1, 2]，对照各个选项可得本题答案． 【解答】解：∵ 正方体ABCD −A 1B 1C 1D 1中，P 为截面A 1BD 内（包括边界）的动点， ∴ 运动点P ，可得①当P 与点B 重合时，C 1P →⋅C 1B →=|C 1B|→2=2，达到最大值； ②当P 点与D 点或A 1点重合时，C 1P →⋅C 1B →达到最小值 ∵ C 1P →⋅C 1B →=(BD →−BC 1→)⋅C 1B →=BD →⋅C 1B →−BC 1→⋅C 1B →BD →⋅C 1B →=−|BD|→⋅|C 1B|→cos 60∘=−1，且BC 1→⋅C 1B →=−|C 1B|→2=−2 ∴ C 1P →⋅C 1B →最小值为−1−(−2)=1综上所述，数量积C 1P →⋅C 1B →的范围为[1, 2]由此可得C 1P →⋅C 1B →的值不可能小于1，A 项不符合题意故选：A二、填空题：本大题共6小题，每小题4分，共24分.把答案填在题中横线上. 【答案】 −2,12【考点】共线向量与共面向量 【解析】先根据三个点A(1, −1, b)，B(2, a, 1)，O(0, 0, 0)在同一条直线上，转化为向量OA →与OB →共线，再利用向量共线的基本定理得存在λ，使得OA →=λOB →，从而建立方程求解即可． 【解答】解：∵ 三个点A(1, −1, b)，B(2, a, 1)，O(0, 0, 0)在同一条直线上， ∴ 向量OA →与OB →共线， 即存在λ，使得OA →=λOB →， 即(1, −1, b)=λ(2, a, 1) ∴ {2λ=1aλ=−1λ=b ，解得{λ=12a =−2b =12故答案为：−2，12．【答案】 a ≥1 【考点】利用导数研究函数的单调性 【解析】求函数的导数，要使函数单调递增，则y ′≥0成立，然后求出实数a 的取值范围． 【解答】解：因为y =ax −sin x ，所以y ′=a −cos x ． 要使函数单调递增，则y ′≥0成立． 即a −cos x ≥0恒成立． 所以a ≥cos x ，因为−1≤cos x ≤1， 所以a ≥1．故答案为；a ≥1． 【答案】 43【考点】定积分【解析】联立解曲线y=x2及直线y=2x，得它们的交点是O(0, 0)和A(2, 2)，由此可得两个图象围成的面积等于函数y=2x−x2在[0, 2]上的积分值，根据定义分计算公式加以计算，即可得到所求面积．【解答】解：由{y=x2y=2x，解得曲线y=x2及直线y=2x的交点为O(0, 0)和A(2, 2)因此，曲线y=x2及直线y=2x所围成的封闭图形的面积是S=∫(202x−x2)dx=(x2−13x3)|02=43．故答案为：43．【答案】√3【考点】直线与平面所成的角【解析】利用线面所成角的定义先确定线面所成的角然后求出线面所成的角即可．【解答】解：过E做EF⊥AB于F，则F为AB的中点．连结CF，则∠ECF为CE与底面ABC所成的角．所以CF=√2，EF=2，所以CE=√6，所以cos∠ECF=CFCE =√2√6=√33．故答案为：√33．【答案】①②④【考点】命题的真假判断与应用【解析】①求函数的导数，判断函数的极值．②由f(x)<0，解不等式即可．③利用函数的单调性和最值之间的关系判断函数的最值情况．④利用导数研究函数的最值．【解答】解：函数的导数为f′(x)=2xe x+(x2−3)e x=(x2+2x−3)e x．①由f′(x)>0得，x>1或x<−3，此时函数单调递增．由f′(x)<0得−3<x<1，此时函数单调递减，所以f(−3)是f(x)的极大值，f(1)是f(x)的极小值，所以①正确．②由f(x)<0，得(x2−3)e x<0，即x2−3<0，解得−√3<x<√3，所以②正确．③由①知，函数在(1, +∞)和(−∞, −3)上单调递增，在(−3, 1)上单调递减，强当x<1时，函数f(x)>0，函数f(x)在x=1时取得极小值同时也是最小值，但没有最大值，所以③错误．④由③(x)有最小值，没有最大值，所以④正确．故答案为：①②④．【答案】x13x+27,(0, 23n−1)【考点】函数的求值函数的值域及其求法归纳推理【解析】根据定义分别计算f1(x)，f2(x)，f3(x)，然后根据前三个函数的值域归纳出f n(x)的表达式，然后利用分式函数求函数的值域即可．【解答】解：根据定义可知f2(x)=f[f1(x)]=xx+3xx+3+3=x4x+9，f3(x)=f[f2(x)]=x4x+9x4x+9+3=x13x+27，f4(x)=x40x+81，所以f n(x)=x12(3n−1)x+3n=23n−1⋅xx+2⋅3n3n−1<23n−1，所以f n(x)的值域为(0, 23n−1)．故答案为：x13x+27，(0, 23n−1)．三、解答题：本大题共4小题，共44分.解答应写出文字说明，证明过程或演算步骤.【答案】解：（1）f′(x)=a2x2−4ax+b，由题意可得f′(0)=b=3．∴b=3．（2）由函数f(x)在x=1处取得极大值，∴f′(1)=a2−4a+3=0，解得a=1或3．①当a=1时，f′(x)=x2−4x+3=(x−1)(x−3)．列表如下：由表格可知：函数f(x)在x=1处取得极大值，满足题意．②同理可得：当a=3时，函数f(x)在x=1处取得极小值，不符合题意，应舍去．综上所述：当a=1时，函数f(x)在x=1处取得极大值．【考点】函数在某点取得极值的条件【解析】（1）利用f′(0)=3即可解出；（2）由函数f(x)在x=1处取得极大值，可得f′(1)=a2−4a+3=0，解得a=1或3．再分别讨论是否符合取得极大值的充分条件即可．【解答】解：（1）f′(x)=a2x2−4ax+b，由题意可得f′(0)=b=3．∴b=3．（2）由函数f(x)在x=1处取得极大值，∴f′(1)=a2−4a+3=0，解得a=1或3．①当a=1时，f′(x)=x2−4x+3=(x−1)(x−3)．列表如下：由表格可知：函数f(x)在x=1处取得极大值，满足题意．②同理可得：当a=3时，函数f(x)在x=1处取得极小值，不符合题意，应舍去．综上所述：当a=1时，函数f(x)在x=1处取得极大值．【答案】解：（1）根据题意，A n是线段A n−2A n−1的中点，则有当n≥3时，x n=x n−1+x n−22．（2）a1=x2−x1=a，a2=x3−x2=x2+x12−x2=−12(x2−x1)=−12a，a3=x4−x3=x3+x22−x3=−12(x3−x2)=−12(−12a)=14a，由此推测：a n=(−12)n−1a(n∈N∗)．证明如下：因为a1=a>0，且a n=x n+1−x n=x n+x n−12−x n=x n−1−x n2=−12(x n−x n−1)=−12a n−1(n≥2)，所以a n=(−12)n−1a．【考点】数列的应用【解析】（1）根据题意，A n是线段A n−2A n−1的中点，可得x n与x n−1、x n−2之间的关系式，（2）由题意知a1=a，a2=−12a，a3=14a，由此推测：a n=(−12)n−1a(n∈N∗)再进行证明．【解答】解：（1）根据题意，A n是线段A n−2A n−1的中点，则有当n≥3时，x n=x n−1+x n−22．（2）a1=x2−x1=a，a2=x3−x2=x2+x12−x2=−12(x2−x1)=−12a，a3=x4−x3=x3+x22−x3=−12(x3−x2)=−12(−12a)=14a，由此推测：a n=(−12)n−1a(n∈N∗)．证明如下：因为a1=a>0，且a n=x n+1−x n=x n+x n−12−x n=x n−1−x n2=−12(x n−x n−1)=−12a n−1(n≥2)，所以a n=(−12)n−1a．【答案】解：（1）证明：平面ADEF⊥平面ABCD，交线为AD，由已知可得AF⊥AD，且AF⊂面ADEF，所以AF⊥平面ABCD，又AB⊥AD，如图，以A为原点建立空间直角坐标系A−xyx，则A(0, 0, 0)，B(4, 0, 0)，C(2, 2√2, 0)，E(0, 2√2, 2)，所以BE→=(−4,2√2,2)，AC→=(2,2√2,0)，所以BE→⋅AC→=0，所以BE⊥AC．（2）由已知可得AD⊥CD，AD⊥DE，设平面CED的一个法向量为n1→=(0,1,0)，平面BCE的法向量为n2→=(x,y,z)，则有{n2→⋅BE→=0n2→⋅BC→=0，即{−4x+2√2y+2z=0−2x+2√2y=0，令y=1，所以平面BCE的一个法向量为n2→=(√2,1,√2)，所以cos <n 1→，n 2→>=n 1→⋅n 2→|n 1→||n 2→|=√55，所以二面角B −CE −D 的余弦值为−√55． （3）设P(0, 0, z)，0≤z ≤2，BP →=(−4,0,z)，设平面ACE 的法向量为n →=(x,y,z)，则{n →⋅AE →=0n →⋅AC →=0，即{2√2y +2z =02x +2√2y =0，不妨设y =1，则平面ACE 的法向量为n →=(−√2,1,−√2)， 由BP →⋅n →=(−4,0,z)⋅(−√2,1,−√2)=0，解得z =4，不符合题意， 即线段AF 上不存在点P ，使BP // 平面ACE ． 【考点】二面角的平面角及求法 用空间向量求平面间的夹角 两条直线垂直的判定 直线与平面垂直的性质 直线与平面平行的判定【解析】（1）建立空间坐标系，利用线面垂直的性质证明BE ⊥AC ； （2）利用向量法求二面角B −CE −D 的余弦值； （3）根据线面平行的判定定理和性质定理确定P 的位置．【解答】 解：（1）证明：平面ADEF ⊥平面ABCD ，交线为AD ，由已知可得AF ⊥AD ，且AF ⊂面ADEF ， 所以AF ⊥平面ABCD ，又AB ⊥AD ，如图，以A 为原点建立空间直角坐标系A −xyx ，则A(0, 0, 0)，B(4, 0, 0)，C(2, 2√2, 0)， E(0, 2√2, 2)，所以BE →=(−4,2√2,2)，AC →=(2,2√2,0)， 所以BE →⋅AC →=0，所以BE ⊥AC ．（2）由已知可得AD ⊥CD ，AD ⊥DE ，设平面CED 的一个法向量为n 1→=(0,1,0)，平面BCE 的法向量为n 2→=(x,y,z)，则有{n 2→⋅BE →=0n 2→⋅BC →=0，即{−4x +2√2y +2z =0−2x +2√2y =0， 令y =1，所以平面BCE 的一个法向量为n 2→=(√2,1,√2)， 所以cos <n 1→，n 2→>=n 1→⋅n 2→|n 1→||n 2→|=√55，所以二面角B −CE −D 的余弦值为−√55． （3）设P(0, 0, z)，0≤z ≤2，BP →=(−4,0,z)，设平面ACE 的法向量为n →=(x,y,z)，则{n →⋅AE →=0n →⋅AC →=0，即{2√2y +2z =02x +2√2y =0，不妨设y =1，则平面ACE 的法向量为n →=(−√2,1,−√2)， 由BP →⋅n →=(−4,0,z)⋅(−√2,1,−√2)=0，解得z =4，不符合题意， 即线段AF 上不存在点P ，使BP // 平面ACE ． 【答案】 解：（1）函数的定义域：(0, +∞)， 当a =−2时，f′(x)=1−4x 22，当x ∈(0, 12)时，f′(x)>0，函数是增函数； 当x ∈(12, +∞)时，f′(x)<0，函数是减函数．因为f(12)=−12−ln 2<0，所以此时在定义域上f(x)<0， s 所以函数f(x)零点的个数为0．； （2）f′(x)=2ax −(a +2)+1x =(ax−1)(2x−1)x，①当a ≤0时，当x ∈(0, 12)时，f′(x)>0，函数是增函数； 当x ∈(12, +∞)时，f′(x)<0，函数是减函数． ②当0<a <2时，当x ∈(0, 12)时，f′(x)>0，函数是增函数；当x ∈(12, 1a )时，f′(x)<0，函数是减函数； 当x ∈(1a , +∞)时，f′(x)>0，函数是增函数． ③当a =2时，f′(x)=(2x−1)2x≥0，对一切x ∈(0, +∞)恒成立，当且仅当x =1时f′(x)=0，函数是单调增函数，单调增区间(0, +∞) ④当a >2时，当x ∈(0, 1a )时，f′(x)>0，函数是增函数； 当x ∈(1a , 12)时，f′(x)<0，函数是减函数； 当x ∈(12, +∞)时，f′(x)>0，函数是增函数．综上：当a ≤0时，函数f(x)的单调增区间(0, 12)，单调减区间是(12,+∞)．当0<a <2时，函数f(x)的单调增区间(0, 12)和(1a ,+∞)，单调减区间是(12,1a )． 当a =2时，函数的单调增区间(0, +∞)当a >2时，函数f(x)的单调增区间(0, 1a )和(12,+∞)，单调减区间是(1a ,12)． 【考点】函数单调性的判断与证明 根的存在性及根的个数判断 利用导数研究函数的单调性【解析】（1）求出函数的定义域，通过a =−2时，求出函数的导函数，判断函数f(x)的极大值，然后推出函数的零点的个数；（2）通过求解函数的导函数，通过：当a ≤0，0<a <2，a =2，a >2，分别通过函数的导数列表，然后求函数f(x)的单调区间．【解答】 解：（1）函数的定义域：(0, +∞)， 当a =−2时，f′(x)=1−4x 22，当x ∈(0, 12)时，f′(x)>0，函数是增函数； 当x ∈(12, +∞)时，f′(x)<0，函数是减函数．因为f(12)=−12−ln 2<0，所以此时在定义域上f(x)<0， s 所以函数f(x)零点的个数为0．； （2）f′(x)=2ax −(a +2)+1x =(ax−1)(2x−1)x，①当a ≤0时，当x ∈(0, 12)时，f′(x)>0，函数是增函数； 当x ∈(12, +∞)时，f′(x)<0，函数是减函数．②当0<a <2时，当x ∈(0, 12)时，f′(x)>0，函数是增函数；当x ∈(12, 1a )时，f′(x)<0，函数是减函数； 当x ∈(1a , +∞)时，f′(x)>0，函数是增函数． ③当a =2时，f′(x)=(2x−1)2x≥0，对一切x ∈(0, +∞)恒成立，当且仅当x =1时f′(x)=0，函数是单调增函数，单调增区间(0, +∞) ④当a >2时，当x ∈(0, 1a )时，f′(x)>0，函数是增函数； 当x ∈(1a , 12)时，f′(x)<0，函数是减函数； 当x ∈(12, +∞)时，f′(x)>0，函数是增函数．综上：当a ≤0时，函数f(x)的单调增区间(0, 12)，单调减区间是(12,+∞)．当0<a <2时，函数f(x)的单调增区间(0, 12)和(1a,+∞)，单调减区间是(12,1a)．当a =2时，函数的单调增区间(0, +∞)当a >2时，函数f(x)的单调增区间(0, 1a )和(12,+∞)，单调减区间是(1a ,12)．。

2013-2014学年北京市海淀区高二（下）期中数学试卷（理科）一、选择题：本大题共8小题，每小题4分，共32分.1．（4分）复数z＝i（i+2）的虚部是（）A．﹣2B．2C．﹣2i D．2i2．（4分）计算dx的结果是（）A．e B．1﹣e﹣2C．1D．e﹣13．（4分）已知函数f（x）的导函数f′（x）的图象如图所示，那么下面说法正确的是（）A．在（﹣3，1）内f（x）是增函数B．在（1，3）内f（x）是减函数C．在（4，5）内f（x）是增函数D．在x＝2时，f（x）取得极小值4．（4分）已知函数f（x）和g（x）在区间[a，b]上的图象如图所示，那么下列说法正确的是（）A．f（x）在a到b之间的平均变化率大于g（x）在a到b之间的平均变化率B．f（x）在a到b之间的平均变化率小于g（x）在a到b之间的平均变化率C．对于任意x0∈（a，b），函数f（x）在x＝x0处的瞬时变化率总大于函数g （x）在x＝x0处的瞬时变化率D．存在x0∈（a，b），使得函数f（x）在x＝x0处的瞬时变化率小于函数g（x）在x＝x0处的瞬时变化率5．（4分）用反证法证明命题“已知A，B，C，D是空间中的四点，直线AB与CD是异面直线，则直线AC和BD也是异面直线．”应假设（）A．直线AC和BD是平行直线B．直线AB和CD是平行直线C．直线AC和BD是共面直线D．直线AB和CD是共面直线6．（4分）已知函数f（x）＝x sin x，记m＝f（﹣），n＝f（），则下列关系正确的是（）A．m＜0＜n B．0＜n＜m C．0＜m＜n D．n＜m＜0 7．（4分）已知曲线y＝g（x）在点（1，g（1））处的切线方程为y＝2x+1，设函数f（x）＝g（2x﹣1），则曲线y＝f（x）在点（1，f（1））处切线方程为（）A．y＝2x+1B．y＝4x﹣1C．y＝2x﹣1D．y＝4x+1 8．（4分）已知定义在R上的函数f（x）的导函数为f′（x），且满足f′（x）＞f（x），则下列结论正确的是（）A．f（1）＞ef（0）B．f（1）＜ef（0）C．f（1）＞f（0）D．f（1）＜f（0）二、填空题：本大题共6小题，每小题4分，共24分.9．（4分）函数f（x）＝x﹣2lnx的单调递增区间为．10．（4分）已知复数z满足|z|≤2，则复数z在复平面内对应的点Z的集合构成的图形的面积是．11．（4分）曲线y＝x2与直线y＝x所围成图形的面积为．12．（4分）设正三棱柱（底边为等边三角形的直棱柱）的体积为2，那么其表面积最小时，底面边长为．13．（4分）观察不等式：1++＜2，1+++…+＜3，1+++…+＜4，1+++…+＜5，…，由此归纳第n个不等式为．要用数学归纳法证明该不等式，由n＝k（k≥1）时不等式成立，推证n＝k+1时，左边应增加的项数为．14．（4分）根据“已知点A（a0，0）是圆C1：+＝1外一点，设不垂直于x轴的直线l与圆C1交于P，Q两点，若x轴是∠P AQ的平分线，则直线l过定点A′（，0）”，通过类比可推知“已知点B（b0，0）是椭圆C2：+＝1（a＞b＞0）外一定点，设不垂直于x轴的直线l′与椭圆C2交于P′，Q′两点，若x轴是∠P′BQ′的平分线，则直线l′过定点B′”．（将点的坐标填入前面的横线上）三、解答题：本大题共4小题，每小题10分，解答应写出文字说明，证明过程或演算步骤.15．（10分）如图，在四棱柱P﹣ABCD中，底面ABCD是矩形，E是棱P A的中点，PD⊥BC．求证：（Ⅰ）PC∥平面BED；（Ⅱ）△PBC是直角三角形．16．（11分）已知函数f（x）＝ax3+3x+2（a∈R）的一个极值点是1．（Ⅰ）求曲线y＝f（x）在点（2，f（2））处的切线方程；（Ⅱ）求函数f（x）在[﹣2，3]上的最大值和最小值．17．（12分）已知函数f（x）＝e a﹣x，其中e是自然对数的底数，a∈R．（Ⅰ）求函数g（x）＝xf（x）的单调区间；（Ⅱ）试确定函数h（x）＝f（x）+x的零点个数，并说明理由．18．（11分）在平面直角坐标系中，对于一条折线C：A1﹣A2﹣…﹣A n，若能再作出一条折线C′：A1﹣B2﹣B3﹣…﹣B n﹣A n，使得A1B2⊥A1A2，B2B3⊥﹣1A2A3，…，B n﹣1A n⊥A n﹣1A n（其中A1，A2，A3，…，A n，B2，B3，…，B n﹣1都是整点），则称折线C′是折线C的一条共轭折线（说明：横、纵坐标均为整数的点成为整点）．（Ⅰ）请分别判断图（1），（2）中，虚折线是否是实折线的一条个，共轭折线；（Ⅱ）试判断命题“对任意的n∈N且n＞2，总存在一条折线C：A1﹣A2﹣…﹣A n有共轭折线”的真假，并举例说明；（Ⅲ）如图（3），折线C：A1﹣A2﹣A3﹣A4，其中A1（0，0），A2（3，1），A3（6，0），A4（9，1）．求证：折线C无共轭折线．2013-2014学年北京市海淀区高二（下）期中数学试卷（理科）参考答案与试题解析一、选择题：本大题共8小题，每小题4分，共32分.1．（4分）复数z＝i（i+2）的虚部是（）A．﹣2B．2C．﹣2i D．2i【解答】解：∵z＝i（i+2）＝﹣1+2i．∴复数z＝i（i+2）的虚部是2．故选：B．2．（4分）计算dx的结果是（）A．e B．1﹣e﹣2C．1D．e﹣1【解答】解：dx＝．故选：C．3．（4分）已知函数f（x）的导函数f′（x）的图象如图所示，那么下面说法正确的是（）A．在（﹣3，1）内f（x）是增函数B．在（1，3）内f（x）是减函数C．在（4，5）内f（x）是增函数D．在x＝2时，f（x）取得极小值【解答】解：①在（﹣3，﹣），（2，4）上，f′（x）＜0，∴f（x）是减函数，②在（﹣，2），（4，5）上，f′（x）＞0，∴f（x）是增函数，③x＝2时，取到极大值；故选：C．4．（4分）已知函数f（x）和g（x）在区间[a，b]上的图象如图所示，那么下列说法正确的是（）A．f（x）在a到b之间的平均变化率大于g（x）在a到b之间的平均变化率B．f（x）在a到b之间的平均变化率小于g（x）在a到b之间的平均变化率C．对于任意x0∈（a，b），函数f（x）在x＝x0处的瞬时变化率总大于函数g （x）在x＝x0处的瞬时变化率D．存在x0∈（a，b），使得函数f（x）在x＝x0处的瞬时变化率小于函数g（x）在x＝x0处的瞬时变化率【解答】解：对于A、B，∵f（x）在a到b之间的平均变化率是，g（x）在a到b之间的平均变化率是，∴＝，即二者相等；∴选项A、B错误；对于C、D，∵函数f（x）在x＝x0处的瞬时变化率是函数f（x）在x＝x0处的导数，即函数f（x）在该点处的切线的斜率，同理函数g（x）在x＝x0处的瞬时变化率是函数g（x）在x＝x0处的导数，即函数g（x）在x＝x0处的切线的斜率，由图形知，选项C错误，D正确．故选：D．5．（4分）用反证法证明命题“已知A，B，C，D是空间中的四点，直线AB与CD是异面直线，则直线AC和BD也是异面直线．”应假设（）A．直线AC和BD是平行直线B．直线AB和CD是平行直线C．直线AC和BD是共面直线D．直线AB和CD是共面直线【解答】解：用反证法证明命题：“若直线AB、CD是异面直线，则直线AC、BD也是异面直线”应假设直线AC、BD是共面直线，故选：C．6．（4分）已知函数f（x）＝x sin x，记m＝f（﹣），n＝f（），则下列关系正确的是（）A．m＜0＜n B．0＜n＜m C．0＜m＜n D．n＜m＜0【解答】解：∵f（x）＝x sin x，∴f（﹣x）＝﹣x sin（﹣x）＝x sin x＝f（x），即函数f（x）是偶函数，∴m＝f（﹣）＝f（）当0时，函数y＝x，单调递增，y＝sin x单调递增，且此时f（x）＞0，∴此时f（x）＝x sin x在0上单调递增，∵＞，∴f（）＞f（）＞0，即f（﹣）＞f（）＞0，∴0＜n＜m，故选：B．7．（4分）已知曲线y＝g（x）在点（1，g（1））处的切线方程为y＝2x+1，设函数f（x）＝g（2x﹣1），则曲线y＝f（x）在点（1，f（1））处切线方程为（）A．y＝2x+1B．y＝4x﹣1C．y＝2x﹣1D．y＝4x+1【解答】解：曲线y＝g（x）在（1，g（1））处的切线是y＝2x+1，则：切点是（1，3），斜率是k＝2，得：g（1）＝3、g'（1）＝2，由f（x）＝g（2x﹣1），得：f′（x）＝2g′（2x﹣1），切线斜率k＝f′（1）＝2g′（1）＝2×2＝4．f（1）＝g（1）＝3，切点是（1，3），得切线是：y﹣3＝4（x﹣1），即：y＝4x﹣1．故选：B．8．（4分）已知定义在R上的函数f（x）的导函数为f′（x），且满足f′（x）＞f（x），则下列结论正确的是（）A．f（1）＞ef（0）B．f（1）＜ef（0）C．f（1）＞f（0）D．f（1）＜f（0）【解答】解：令g（x）＝，则g′（x）＝＝，∵f′（x）＞f（x），∴g′（x）＞0，g（x）递增，∴g（1）＞g（0），即，∴f（1）＞ef（0），故选：A．二、填空题：本大题共6小题，每小题4分，共24分.9．（4分）函数f（x）＝x﹣2lnx的单调递增区间为（2，+∞）．【解答】解：由题意知函数的定义域为（0，+∞）．函数f（x）＝x﹣2lnx的导数为，由f'（x）＞0，即，解得x＞2．此时函数单调递增．所以函数f（x）＝x﹣2lnx的单调增区间为（2，+∞）．故答案为：（2，+∞）．10．（4分）已知复数z满足|z|≤2，则复数z在复平面内对应的点Z的集合构成的图形的面积是4π．【解答】解：设z＝x+yi（x，y∈R），由|z|≤2，得，即x2+y2≤4．∴复数z在复平面内对应的点Z的集合构成的图形是半径为2的圆．其面积为4π．故答案为：4π．11．（4分）曲线y ＝x 2与直线y ＝x 所围成图形的面积为 ．【解答】解：先根据题意画出图形，得到积分上限为1，积分下限为0直线y ＝x 与曲线y ＝x 2所围图形的面积S ＝∫01（x ﹣x 2）dx而∫01（x ﹣x 2）dx ＝（ ﹣）|01＝﹣＝∴曲边梯形的面积是故答案为：．12．（4分）设正三棱柱（底边为等边三角形的直棱柱）的体积为2，那么其表面积最小时，底面边长为 2 ．【解答】解：设正三棱柱的底面边长为x ，高为h ，∵体积为2，∴×x 2×h ＝2，∴h ＝，∴棱柱的表面积S ＝2××x 2+3xh ＝x 2+＝x 2++≥6， 当x 3＝8时，即x ＝2时，取“＝”．故答案为：2．13．（4分）观察不等式：1++＜2，1+++…+＜3，1+++…+＜4，1+++…+＜5，…，由此归纳第n 个不等式为．要用数学归纳法证明该不等式，由n＝k（k≥1）时不等式成立，推证n＝k+1时，左边应增加的项数为2k+1．【解答】解：第一空：∵不等式的右侧：2＝1+1，3＝2+1，4＝3+1，…左侧：每一项分别有：22﹣1，23﹣1，24﹣1，…项，每一项中最后一项的分母为：．∴由此归纳第n个不等式为：，第二空：左边的特点：分母逐渐增加1，末项为；由n＝k，末项为，到n＝k+1，末项为，∴应增加的项数为2k+1．故答案为：；2k+1（注：每空2分）14．（4分）根据“已知点A（a0，0）是圆C1：+＝1外一点，设不垂直于x轴的直线l与圆C1交于P，Q两点，若x轴是∠P AQ的平分线，则直线l过定点A′（，0）”，通过类比可推知“已知点B（b0，0）是椭圆C2：+＝1（a＞b＞0）外一定点，设不垂直于x轴的直线l′与椭圆C2交于P′，Q′两点，若x轴是∠P′BQ′的平分线，则直线l′过定点B′”．（将点的坐标填入前面的横线上）【解答】解：根据“已知点A（a0，0）是圆C1：+＝1外一点，设不垂直于x轴的直线l与圆C1交于P，Q两点，若x轴是∠P AQ的平分线，则直线l 过定点A′（，0）”中，A′点横坐标的分子为的分母，分子是A点的横坐标，可以类比得到：“已知点B（b0，0）是椭圆C2：+＝1（a＞b＞0）外一定点，设不垂直于x轴的直线l′与椭圆C2交于P′，Q′两点，若x轴是∠P′BQ′的平分线，则直线l′过定点B′，故答案为：（注：回答出给（4分）；答案为或或给（3分）；其它答案酌情给1～（2分）；未作答，给0分）三、解答题：本大题共4小题，每小题10分，解答应写出文字说明，证明过程或演算步骤.15．（10分）如图，在四棱柱P﹣ABCD中，底面ABCD是矩形，E是棱P A的中点，PD⊥BC．求证：（Ⅰ）PC∥平面BED；（Ⅱ）△PBC是直角三角形．【解答】证明：（Ⅰ）连接AC交BD于点O，连接OE．在矩形ABCD中，AO＝OC．因为AE＝EP，所以OE∥PC．因为PC⊄平面BDE，OE⊂平面BDE，所以PC∥平面BDE．（Ⅱ）在矩形ABCD中，BC⊥CD．因为PD⊥BC，CD∩PD＝D，PD⊂平面PDC，DC⊂平面PDC，所以BC⊥平面PDC．因为PC⊂平面PDC，所以BC⊥PC．即△PBC是直角三角形．16．（11分）已知函数f（x）＝ax3+3x+2（a∈R）的一个极值点是1．（Ⅰ）求曲线y＝f（x）在点（2，f（2））处的切线方程；（Ⅱ）求函数f（x）在[﹣2，3]上的最大值和最小值．【解答】解：（Ⅰ）∵f（x）＝ax3+3x+2，∴f'（x）＝3ax2+3．∵函数f（x）的一个极值点是1，∴f'（1）＝3a+3＝0．解得：a＝﹣1．经检验，a＝﹣1满足题意．∴f（x）＝﹣x3+3x+2，∴f（2）＝0，f'（2）＝﹣9．∴曲线y＝f（x）在点（2，f（2））处的切线方程是y＝﹣9（x﹣2），即9x+y﹣18＝0．（Ⅱ）由（Ⅰ）知：f'（x）＝﹣3x2+3．令f'（x）＝0，得x1＝﹣1，x2＝1．当x在[﹣2，3]上变化时，f'（x），f（x）的变化情况如下表∴函数f（x）在[﹣2，3]上的最大值为4，最小值为﹣16．17．（12分）已知函数f（x）＝e a﹣x，其中e是自然对数的底数，a∈R．（Ⅰ）求函数g（x）＝xf（x）的单调区间；（Ⅱ）试确定函数h（x）＝f（x）+x的零点个数，并说明理由．【解答】解：（Ⅰ）∵g（x）＝xe a﹣x，x∈R，∴g'（x）＝（1﹣x）e a﹣x．令g'（x）＝0，得x＝1．当x变化时，g（x）和g'（x）的变化情况如下：故g（x）的单调递减区间为（1，+∞）；单调递增区间为（﹣∞，1）．（Ⅱ）∵h（x）＝e a﹣x+x，∴h'（x）＝1﹣e a﹣x．令h'（x）＝0，得x＝a．当x变化时，h（x）和h'（x）的变化情况如下：即h（x）的单调递增区间为（a，+∞）；单调递减区间为（﹣∞，a）．∴h（x）的最小值为h（a）＝1+a．①当1+a＞0，即a＞﹣1时，函数h（x）不存在零点．②当1+a＝0，即a＝﹣1时，函数h（x）有一个零点．③当1+a＜0，即a＜﹣1时，h（0）＝e a＞0，下证：h（2a）＞0．令m（x）＝e x﹣2x，则m'（x）＝e x﹣2．解m'（x）＝e x﹣2＝0得x＝ln2．当x＞ln2时，m'（x）＞0，∴函数m（x）在[ln2，+∞）上是增函数．取x＝﹣a＞1＞ln2，得：m（﹣a）＝e﹣a+2a＞e ln2﹣2ln2＝2﹣2ln2＞0．∴h（2a）＝e﹣a+2a＝m（﹣a）＞0．结合函数h（x）的单调性可知，此时函数h（x）有两个零点．综上，当a＞﹣1时，函数h（x）不存在零点；a＝﹣1时，函数h（x）有一个零点；当a＜﹣1时，函数h（x）有两个零点．18．（11分）在平面直角坐标系中，对于一条折线C：A1﹣A2﹣…﹣A n，若能再﹣A n，使得A1B2⊥A1A2，B2B3⊥作出一条折线C′：A1﹣B2﹣B3﹣…﹣B n﹣1A2A3，…，B n﹣1A n⊥A n﹣1A n（其中A1，A2，A3，…，A n，B2，B3，…，B n﹣1都是整点），则称折线C′是折线C的一条共轭折线（说明：横、纵坐标均为整数的点成为整点）．（Ⅰ）请分别判断图（1），（2）中，虚折线是否是实折线的一条个，共轭折线；（Ⅱ）试判断命题“对任意的n∈N且n＞2，总存在一条折线C：A1﹣A2﹣…﹣A n有共轭折线”的真假，并举例说明；（Ⅲ）如图（3），折线C：A1﹣A2﹣A3﹣A4，其中A1（0，0），A2（3，1），A3（6，0），A4（9，1）．求证：折线C无共轭折线．【解答】解：（Ⅰ）（1）不是，因为线段A1B2与线段A1A2不垂直；（2）不是，因为线段B2B3与线段A2A3不垂直．…（2分）（Ⅱ）命题“对任意n∈N且n＞2，总存在一条折线C：A1﹣A2﹣…﹣A n有共轭折线”是真命题．理由如下：当n为奇数时，不妨令n＝2k﹣1，k＝2，3，4，…，取折线C：A1﹣A2﹣…﹣A2k．其中A i（a i，b i）（i＝1，2，…，2k﹣1），﹣1＝0（i＝1，2，…，k），b2i＝1（i＝1，满足a i＝i﹣1（i＝1，2，…，2k﹣1），b2i﹣12，…，k﹣1）．则折线C的共轭折线为折线C关于x轴对称的折线．如图所示．当n为偶数时，不妨令n＝2k，k＝2，3，4，…，取折线C：A1﹣A2﹣…﹣A2k．其中A i（a i，b i）（i＝1，2，…，2k），满足a i＝i﹣1（i＝1，2，…，2k﹣1），a2k＝2k，b2i＝0（i＝1，2，…，k），b2i﹣1＝1（i＝1，2，…，k）．折线C的共轭折线为折线C'：B1﹣B2﹣…﹣B2k．其中B i（x i，y i）（i＝1，2，…，2k）满足：x i＝i﹣1（i＝1，2，…，2k﹣3），x2k﹣2＝2k﹣1，x2k﹣1＝2k+1，x2k＝2k，y2i﹣1＝0（i＝1，2，…，k﹣1），y2i＝﹣1（i＝1，2，…，k﹣2），y2k﹣2＝﹣3，y2k﹣1＝﹣1，y2k＝1．如图所示．…（7分）注：本题答案不唯一．证明：（Ⅲ）假设折线B1﹣B2﹣B3﹣B4是题设中折线C的一条共轭折线（其中B1＝A1，B4＝A4），设（t＝1，2，3），显然x t，y t为整数．则由B t B t+1⊥A t A t+1，得：由①②③式得这与⑤式矛盾，因此，折线C无共轭折线．…（11分）。

北京四中2013－2014学年下学期高二年级期中考试数学试卷（文）试卷分为两卷，卷（Ⅰ）100分，卷（Ⅱ）50分，共计150分，考试时间120分钟卷（Ⅰ）《选修1－1》一、选择题（本大题共8小题，每小题5分，共40分） 1．抛物线x 2=－8y 的焦点坐标为A. （0，－4）B. （0，－2）C. 1(0,)16-D. 1(0,)32- 2．下列函数求导运算正确的个数为 ①(21)'2x -=；②21(log )'ln 2x x =⋅；③()'x x e e =；④(cos )'sin x x = A ．1 B ．2 C ．3 D ．43．函数()2cos f x x x =+在[0，π]上的极大值点为 A.12π B. 6π C. 3π D. 2π4．下列命题中，是假命题的是A ．如果x<2，则x<3B ．3+6=8或3+6=9C ．2,0x R x ∀∈> D. *x N ∃∈，使x 既是质数又是偶数5．若偶函数f （x ）定义域为(,0)(0,)-∞+∞，f （x ）在（0,+∞）上的图象如图所示，则不等式f （x ）f'（x ）>0的解集是A. (,1)(0,1)-∞-B. (1,0)(1,)-+∞C. (,1)(1,)-∞-+∞D. (1,0)(0,1)-6．若ln (),3xf x a b x=<<，则 A ．()()f a f b > B ．()()f a f b = C ．()()f a f b < D ．()()1f a f b >7. 已知抛物线22y x =上两点11(,)A x y ，22(,)B x y 关于直线y x m =+对称，若1212x x =-，则m 的值为A.23 B. 2 C. 52 D. 328. 已知函数1()ln(1)f x x x=+-，则()y f x =的图象大致可能为二、填空题（本大题共4小题，每小题5分，共20分）9. 若命题2:,2p x N x x ∃∈=+，则p ⌝为： 。

北京市海淀区教师进修学校附属实验中学2012-2013学年高二下学期期中（理）第Ⅰ卷 (选择题，共60分)一、选择题：本大题共12小题，每小题5分，共60分.1. 下列命题中，错误．．的是 A ．人的身高和体重具有相关关系B ．简单随机抽样中，每个个体被抽到的概率相等C ．因为正方体边长越大，体积越大，所以正方体的体积和边长呈正相关关系D ．回归分析中，相关指数2R 越接近1，说明模型的拟合效果越好 2. x xx x f +-=1ln )(，设其在0x 处有最大值，则下列说法正确的是 A. 21)(0>x f B. 21)(0<x fC. 21)(0=x fD. )(0x f 与21的大小关系不确定3. "0">a 是"0">a 的 （ ）A ．充分不必要条件 B. 必要不充分条件C. 充要条件D. 既不充分也不必要条件4.设3log 2=P ，2log 3=Q ，)2(log log 32=R ，则 （ ） A. P Q R << B. Q R P << C. P R Q << D. Q P R <<5. 当a ≠0时，函数y ax b =+和y b ax=的图象只可能是 （ ）6．某中学有同样的画册2本，同样的集邮册3本，从中取出4本赠送给4位朋友，每位朋友1本，则不同的赠送方法共有（ ）A 4种B 10种C 18种D 20种 7．下列说法错误的是( )A 命题“若x 2－4x ＋3＝0，则x ＝3”的逆否命题是：“若x ≠3，则x 2－4x ＋3≠0” B “x >1”是“|x |>0”的充分不必要条件 C 若p 且q 为假命题，则p 、q 均为假命题D 命题p ：“∃x 0∈R 使得x 20＋x 0＋1<0”，则⌝p ：“∀x ∈R ，均有x 2＋x ＋1≥0”8．若点P 是曲线y ＝x 2－ln x 上任意一点，则点P 到直线y ＝x －2的最小距离为( )A 1B 2 C22D 3 9. 已知抛物线C:x y 42=的焦点为F ，直线42-=x y 与C 交于A,B 两点，则 COS ∠AFB= ( ) A54 B 53 C —53 D —54 10．在ΔABC 中，∠CAB=∠CBA=30°，AC ，BC 边上的高分别为BD ，AE ，则以A ，B 为焦点，且过D ，E 的椭圆与双曲线的离心率的倒数和为 ( )A 3B 1C 23D 2 11.曲线C ：⎩⎨⎧+=-=1sin 1cos θθy x ，（θ为参数）的普通方程为 （ ） A ．()()11122=++-y x B. ()()11122=+++y xC.()()11122=-++y x D. ()()11122=-+-y x12.极坐标方程θρcos =和参数方程参数）为 (21t t y tx ⎩⎨⎧+=--=所表示的图形分别是（ ）A.直线，直线B.直线，圆C.圆，圆D.圆，直线第Ⅱ卷 （90分）二．填空题：本大题共4小题，每小题5分，共20分。

海淀区高二年级第一学期期末练习数学（理科）参考答案及评分标准2014．01 一. 选择题：本大题共8小题，每小题4分，共32分.题：本大题共6小题，每小题4分，共24分.（9）103（10）10y-=（11）32或1（12（13（14）①②④注：（11）题少一个答案扣2分.三.解答题：本大题共4小题，共44分.解答应写出文字说明，证明过程或演算步骤.（15）（本小题满分10分）解：（Ⅰ）设(,)M x y，则(0,)N y，(,)OM x y=，(4,)NA y=-.……………………2分因为直线MO NA⊥，所以240OM NA xy⋅=-=，即24y x=. ………………………4分所以动点M的轨迹C的方程为24y x=（0x≠）. ………………………5分（Ⅱ）当π6MOA∠=时，因为MO NA⊥，所以π3NAO∠=.所以直线AN的倾斜角为π3或2π3.当直线AN的倾斜角为π3时，直线NAy--=；……………8分当直线AN的倾斜角为2π3时，直线NA0y+-=.…………10分（16）（本小题满分11分）解：（Ⅰ）原方程等价于221412x y+=.由方程可知：212a=，24b=，2228c a b=-=，c=……………………3分所以椭圆C的焦点坐标为(0,，(0,-，长轴长2a为……………5分（Ⅱ）由2231220x yx y⎧+=⎨--=⎩，，可得:220x x--=.解得：2x =或1x =-.所以 点,A B 的坐标分别为(2,0)，(1,3)--. ………………………7分 所以 ,A B 中点坐标为13(,)22-，||AB =……………9分所以 以线段AB 为直径的圆的圆心坐标为13(,)22-. 所以 以线段AB 为直径的圆的方程为22139()()222x y -++=. …………………11分（17）（本小题满分11分）（Ⅰ）证明：在正方形ABCD 中，CD AD ⊥.因为CD PD ⊥，ADPD D =，所以 CD ⊥平面PAD ． ………………………1分 因为 PA ⊂平面PAD ，所以 CD PA ⊥． ………………………2分 同理，BC PA ⊥． 因为 BCCD C =，所以 PA ⊥平面ABCD ． ………………………3分 （Ⅱ）解：连接AC ，由（Ⅰ）知PA ⊥平面ABCD ．因为 AC ⊂平面ABCD ，所以 PA AC ⊥． ………………………4分 因为PC =AC =所以 1PA =．分别以AD ，AB ，AP 所在的直线分别为x ，y ，z 轴，建立空间直角坐标系，如图所示.由题意可得：(0,1,0)B ，(1,0,0)D ，(1,1,0)C ，(0,0,1)P ． 所以(0,1,0)DC =，(1,0,1)DP =-，(1,1,0)BD =-，(0,1,1)BP =-．设平面PDC 的一个法向量(,,)x y z =n ，则00DC DP ⎧⋅=⎪⎨⋅=⎪⎩，，n n 即0,0.y x z =⎧⎨-+=⎩令1x =，得1z =.所以 (1,0,1)=n ．同理可求：平面PDB 的一个法向量(1,1,1)=m ． ………………………6分所以 二面角B PD C --的余弦值为3………………………8分 （Ⅲ）存在．理由如下：若棱PD 上存在点E 满足条件，设(,0,)PE PD λλλ==-，[0,1]λ∈．所以 (1,1,1)(,0,)(1,1,1)EC PC PE λλλλ=-=---=--．…………………9分 因为 平面BCD 的一个法向量为(0,0,1)AP =． 所以 |cos ,|2(1EC AP EC AP EC AP⋅<>==令1sin 30,2==解得：12λ=±. 经检验1[0,1]2λ=-．所以 棱PD 上存在点E ，使直线EC 与平面BCD 所成的角是30，此时PE 的长为1． ………………………11分（18）（本小题满分12分）解：（Ⅰ）由22222222222222221(1)1112a b a b a b a b ⎛⎛⎫ ⎪-⎝⎭⎝⎭⎝⎭⎝⎭+<+=+<+知，31(2P 和5(1,1)P 不在椭圆M 上，即椭圆M 经过1(1,P -，2(0,1)P ，4P . 于是222,1a b ==.所以 椭圆M 的方程为：2212x y +=. ………………………2分 （Ⅱ）①当90A ∠=︒时，设直线:BC x ty m =+，由2222,,x y x ty m ⎧+=⎨=+⎩得222(2)2(2)0t y tmy m +++-=.设1122(,),(,)B x y C x y ，则2216880m t ∆=-+>，12221222,22. 2tm y y t m y y t ⎧+=-⎪⎪+⎨-⎪=⎪+⎩所以AB AC k k ===1==-.于是3m =-，此时21616809t ∆=-+>，所以直线:3BC x ty =-. 因为12216902y y t =-<+，故线段BC 与x轴相交于(,0)3M -，即原点在线段AM 的延长线上，即原点在ABC ∆的外部，符合题设. ………………………6分所以12121||||||23ABC S AM y y y y ∆=⋅-=-====89. 当0t =时取到最大值89. ………………………9分 ②当90A ∠≠︒时，不妨设90B ∠=︒.设直线:0)AB x ty t =-≠，由2222,x y x ty ⎧+=⎪⎨=⎪⎩得22(2)0t y +-=.所以 0y =或y =.所以B ，由AB BC ⊥，可得直线:BC y tx =-.WORD 完整版----可编辑----教育资料分享----完整版学习资料分享----由223222, ,2x y y tx t ⎧+=⎪⎨=-+⎪+⎩得22222328(1)(2)(21)02t t t t y y t +++--=+. 所以 222228(1)0(2)(21)B C t t y y t t +=-<++.所以 线段BC 与x轴相交于N .显然原点在线段AN 上，即原点在ABC ∆的内部，不符合题设. 综上所述，所求的ABC ∆面积的最大值为89.……………………12分注：对于其它正确解法，相应给分.。

海淀区高二年级第二学期期中练习数学（文科）参考答案及评分标准 2014．04一. 选择题：本大题共8小题，每小题4分，共32分.二.填空题：本大题共6小题，每小题4分，共24分.（9）(1,1) （10）ππcosisin33n n + （11）1212120x x y y z z ++= （12）53i -+ （13）66 （14）1(,1)2，2014注：（12）若填i a b -给1分；（14）题每空2分.三.解答题：本大题共4小题，共44分.解答应写出文字说明，证明过程或演算步骤. （15）（本小题满分10分）证明：（Ⅰ）连接AC 交BD 于点O ，连接OE . 在矩形ABCD 中，AO OC =. 因为 AE EP =，所以 OE ∥PC . ………………………2分 因为 PC Ë平面BDE ，OE Ì平面BDE ， 所以 PC ∥平面BDE . ………………………5分 （Ⅱ）在矩形ABCD 中，BC CD ^. 因为 PD BC ^，CDPD D =，PD Ì平面PDC ，DC Ì平面PDC ，所以 BC ^平面PDC . ………………………8分 因为 PC Ì平面PDC ，所以 BC PC ^. ………………………10分OAEBCDP（16）（本小题满分10分）证明：充分性：假设方程()0f x =至少有一个整数根0x .则 2000x bx c ++=. ………………………2分 若0x 是奇数，因为,b c 均为奇数，所以200x bx c ++为奇数，不可能为0，矛盾；………………………4分若0x 是偶数，因为,b c 均为奇数，所以200x bx c ++为奇数，不可能为0，矛盾.所以 方程()0f x =无整数根.所以 “,b c 均为奇数”是“方程()0f x =无整数根”的充分条件. ……………………6分不必要性：令1,2b c ==，方程()0f x =即220x x ++=显然无整数根，但此时c 为偶数.所以 “,b c 均为奇数”是“方程()0f x =无整数根”的不必要条件.综上所述，“,b c 均为奇数”是“方程()0f x =无整数根”的充分而不必要条件.………………………10分（17）（本小题满分12分） 解：（Ⅰ）如图所示. ………………………2分（Ⅱ）因为散点图中的最左侧点和最右侧点分别是（2，3），（6，6.2）， 所以 直线l 的方程是： 6.233(2)62y x --=--，即4570x y -+=. …………………5分 （Ⅲ）由题意可设直线l 的方程为(4)5y k x =-+. ………………………6分 则维修费用的每一个观察值与直线l 上对应点的纵坐标的差的绝对值之和()3(25) 4.4(5) 5.6(5) 6.2(25)S k k k k k =--++--++-++-+2140.6k k =-+- 4.46, 020.4, 0.61, 64.4, 1.k k k k k k -≤⎧⎪=-<≤⎨⎪->⎩………………………9分因为 函数()S k 的单调递增区间是(0.6,)+∞，单调递减区间是(,0.6)-∞，所以 当0.6k =时，()S k 取得最小值0.8，此时直线l 的方程是35130x y -+=.………………………12分（18）（本小题满分12分）（Ⅰ）解：（1）不是，因为线段23B B 与线段23A A 不垂直；（2）是，符合定义. ………………………2分 （Ⅱ）命题“对任意n ∈N 且2n >，总存在一条折线12n C A A A ---：有共轭折线”是真命题.理由如下：当n 为奇数时，不妨令21,2,3,4,n k k =-=，取折线1221k C A A A ----：.其中(,)(1,2,,21)i i i A a b i k =-，满足2121(1,2,,21),0(1,2,,),1(1,2,,1)i i i a i i k b i k b i k -=-=-====-.则折线C 的共轭折线为折线C 关于x 轴对称的折线.如图所示.当n 为偶数时，不妨令2,2,3,4,n k k ==，取折线122k C A A A ---：.其中(,)(1,2,,2)i i i A a b i k =，满足22121(1,2,,21),2,0(1,2,,),1(1,2,,)i k i i a i i k a k b i k b i k -=-=-=====.折线C的共轭折线为折线122'k C B B B ---：.其中(,)(1,2,,2)i i i B x y i k =满足22212211(1,2,,23),21,21,2,0(1,2,,1),i k k k i x i i k x k x k x k y i k ---=-=-=-=+===-2222121(1,2,,2),3,1,1i k k k y i k y y y --=-=-=-=-=.如图所示. ………………………7分注：本题答案不唯一.（Ⅲ）证明：假设折线1234B B B B ---是题设中折线C 的一条共轭折线（其中11B A =，44B A =），设1(,)t t t t B B x y += (1,2,3t =)，显然,t t x y 为整数. 则由11t t t t B B A A ++⊥，得：11223312312330, 30, 30, 9, 1. x y x y x y x x x y y y +=⎧⎪-=⎪⎪+=⎨⎪++=⎪⎪++=⎩①②③④⑤由①②③式得11223,,.3333y x y x y x =-⎧⎪=⎨⎪=-⎩这与⑤式矛盾，因此，折线C 无共轭折线. ………………………12分注：对于其它正确解法，相应给分.。

北京市海淀区2013-2014学年高一下学期期中考试数学试卷（带解析）1．若12( ）【解析】考点：等差中项.2( ）【解析】考点：余弦二倍角公式.3．在△ABC( ）【解析】试题分析：根据已知三边求一角,考点：余弦定理.4( ）【解析】试题分析：根据函数解析式的特点,则根据正弦和角公式,可知,考点：正余弦特殊值,正弦和角公式,正弦函数最值.51 ( ）【解析】根据等比数列通项性所可得6 ( ）【解析】试题分析：根据数列通项公式的特点,可得考点：裂项相消法求数列的和.710 ( ）A.28B.49C.50D.52【解析】试题分析：根据等差数列和公式,可所以可知1,55,则根据等差数列通项49.,通项公式.8．若在△ABC ABC一定是 ( ）A.锐角三角形B.钝角三角形C.直角三角形D.等腰三角形【解析】试题分析：根据内角和为,可知所以三角形是等腰三角形.考点：利用角度判断三角形形状,三角函数诱导公式.9．在△ABC ABC的面积为 .【解析】考点：三角形面积.10【解析】试题分析：根据正切函数的定义有,根据正切和角公式有考点：正切定义,正切和角公式.11是，的最小值为 .【解析】显然根据二次函数的性质可知,.二次函数的性质,查.12．已知在△ABC中，则下列说法中：①△ABC为钝角三角形；正确说法的序号是 .（填上所有正确说法的序号）【答案】①②③【解析】试题分析：根据向量的数量积运算可知因为向量的模长为正,所又因为在三角形中,所钝角,故①正确；根据余弦定理，有b，故②正确；因为故③正确.考点：向量的数量积公式，余弦定理，余弦和角公式.13= ，10= .【解析】试题分析：根据,可得为首项,构成以为首项,为公比的等比数列,所以考点：数列的分析,等比数列的求和公式,通项公式.14（1（2的取值范围是 .【答案】（1）0或1 （2))3234(,(,【解析】试题分析：（1）因相邻两项,根据题意有两种情况,（2）有以下几种情况:舍;:,成立;,所此所以舍;, 当时,即,因为当时,,即,因为不成立;舍;考点：递推公式中的分类讨论.15（1（2（3.【答案】【解析】试题分析：（1）中直接带入角求值即可.(2)要求最值及周期,得将函数解析式转化为或所以化简三角函数.需要用到辅助角公式化简，而后直接判断最小值，利用周期公式求周期.(3)根据(2)中的化简后的函数式,利用三角函数单调性解决.(2)所以（3考点：三角函数求特殊值,三角函数化简求最值和周期,三角函数求单调区间.16（1（2（3.【答案】【解析】 试题分析：(1)法一:根据数列是等差数列,求出首项和公差,得通项公式;法二:,根据等式相等关系,从而得到通项公式.(2)(1)中的结论直接求即可. (3)根据(1)中结论,以及等比中项可解该问.(1)(2)（3舍掉） ,… 考点：等差数列通项公式,,等比中项. 17．已知△ABC（1）求∠B 的值；（2）若点E,P 分别在边AB,BC 上，且AE=4，AP ⊥CE ，求AP 的长； 【答案】【解析】 试题分析：(1).(2),可知利用正弦定理利用余弦定理可知.从而解决问题.(1)根据题意,（2）由(1)知三角形是等腰直角三角形,且斜边为6,考点：正弦定理,余弦定理.18APCEB（1（2出这个数列的前6项，若没有，说明理由；（3.【答案】存在(3)1【解析】试题分析：(1),,.(2)罗列出所有的可能数列,的即可.(3), 因此5个奇数，5(1) 可得(2) 存在这个数列的前6项可以为（3 15个奇数，5个偶数，令这10（或者为考点：数列的综合应用.。