第11章时间数列分析
- 格式:doc
- 大小:46.50 KB
- 文档页数:3



应用统计学时间数列分析概述时间数列分析是统计学中的一种重要方法,它用来研究时间序列数据的特征和规律。
时间数列是指按照时间顺序排列的一组数据,比如每日的股票价格、每年的降雨量等。
通过对时间数列进行统计分析,可以揭示数据背后的趋势、周期和随机性,有助于进行预测和决策。
时间数列分析的主要目的是找到数列中的模式和规律。
常用的时间数列分析方法包括描述性统计、周期性分析、趋势分析和随机性分析。
描述性统计是最基本的统计分析方法,它用来描述和总结数据的特征。
常用的描述性统计指标包括平均值、标准差、最大值、最小值和中位数等。
这些指标可以帮助研究人员了解数据的中心趋势、离散程度和分布形态。
周期性分析是用来检测数据中是否存在重复的模式或周期。
周期性分析常常使用谱分析方法,通过将时间数列转换为频域,提取出数据中的主要周期成分。
这些成分可以帮助预测未来的周期性变化,并优化决策。
趋势分析是用来观察数据的长期变化趋势。
常用的趋势分析方法有移动平均法、指数平滑法和回归分析法等。
这些方法可以拟合出数据的趋势线,帮助判断未来的发展方向和速度。
随机性分析是用来研究数据中的随机波动和不规则性。
常用的随机性分析方法有自相关分析、白噪声检验和单位根检验等。
这些方法可以判断数据中是否存在随机波动,并提供相关的统计验证。
通过应用时间数列分析方法,可以获得关于数据特征、周期性、趋势和随机性的深入洞察。
这些洞察可以用于预测未来的发展趋势、制定决策策略和优化资源配置。
时间数列分析在金融、经济、气象、环境等领域具有广泛的应用价值。
时间数列分析作为统计学的重要方法,具有广泛的应用领域和深远的研究价值。
在金融领域,时间数列分析可以用来预测股票价格、汇率、利率等金融指标,帮助投资者制定投资策略。
在经济学中,时间数列分析可以研究经济增长、通胀、失业率等宏观经济指标的变化规律,为政府制定经济政策提供参考。
在气象和环境领域,时间数列分析可以揭示气候变化、环境污染等问题的趋势和周期,为环境保护和资源利用提供支持。

应用统计学时间数列分析时间数列分析是统计学中的一项重要内容,通过对时间序列数据进行分析,可以揭示数据之间的内在关联和规律。
本文将探讨时间数列分析在实际应用中的重要性和方法。
什么是时间数列分析时间数列(Time Series)指的是按时间顺序排列的一系列数据观测值。
时间数列分析是指根据时间数列数据进行的统计分析方法,旨在发现数据中存在的趋势、季节性、周期性等规律,以便进行预测和决策。
时间数列分析的重要性时间数列分析在许多领域都有广泛的应用,包括经济学、金融、医学、气象等。
通过时间数列分析,我们可以:•发现数据中的趋势和规律•预测未来数据走势•制定决策和策略•检验模型的有效性•揭示不同变量之间的关联时间数列分析方法1. 平稳性检验平稳性是时间数列分析的前提条件之一,可以通过单位根检验、ADF检验等方法来判断时间数列是否平稳。
如果时间数列不平稳,需要进行差分处理或其他转换方法使其平稳化。
2. 自相关性分析自相关性分析是检验数据是否存在自相关性(即相邻数据之间的相关性)的方法,可以通过自相关图和偏自相关图来判断数据中的自相关性程度。
3. 移动平均法移动平均法是一种基本的时间数列预测方法,通过计算一定窗口内的数据均值来平滑数据曲线,以便更好地观察数据走势和预测未来走向。
4. 季节性调整在时间数列分析中,常常需要对数据进行季节性调整,以消除季节性影响,使预测结果更为准确。
应用实例1. 股票价格预测时间数列分析在金融领域有着广泛的应用。
通过分析股票价格的时间数列数据,可以预测股价的未来走势,指导投资决策。
2. 气象预测气象数据也是时间数列数据的一种,通过对气象数据进行时间数列分析,可以预测未来的气候变化和天气情况,为灾害预警和农业生产提供依据。
3. 经济指标分析经济数据的时间数列分析可以揭示经济增长趋势、波动周期等信息,帮助政府和企业做出相应决策。
结语时间数列分析是统计学中一个重要的分析方法,通过对时间序列数据进行分析,可以揭示数据之间的规律、趋势和关联。

时间序列分析课后习题答案TPMK standardization office【 TPMK5AB- TPMK08- TPMK2C- TPMK18】第9章 时间序列分析课后习题答案第10章(1)30× 31.06×21.05= 30×1.3131 = 39.393(万辆)(2117.11%= (3)设按7.4%的增长速度n 年可翻一番则有 1.07460/302n ==所以 n = log2 / log1.074 = 9.71(年)故能提前0.29年达到翻一番的预定目标。
第11章 (1)以1987年为基期,2003年与1987年相比该地区社会商品零售额共增长:(2)年平均增长速度为1%)8.61(%)2.81(%)101(15555-+⨯+⨯+=0.0833=8.33%(3) 2004年的社会商品零售额应为509.52)0833.01(307=+⨯(亿元)第12章 (1)发展总速度%12.259%)81(%)101(%)121(343=+⨯+⨯+ 平均增长速度=%9892.91%12.25910=-(2)8.561%)61(5002=+⨯(亿元)(3)平均数∑====415.142457041j j y y (亿元),2002年一季度的计划任务:625.1495.142%105=⨯(亿元)。
第13章(1)用每股收益与年份序号回归得^0.3650.193t Y t =+。
预测下一年(第11年)的每股收益为488.211193.0365.0ˆ11=⨯+=Y 元(2)时间数列数据表明该公司股票收益逐年增加,趋势方程也表明平均每年增长0.193元。
是一个较为适合的投资方向。
第14章 (1)移动平均法消除季节变动计算表(2)t T t ⨯+=63995.09625.8ˆ(3)趋势剔出法季节比例计算表(一)上表中,其趋势拟合为直线方程t T t ⨯+=63995.09625.8ˆ。


时间数列分析时间数列是指按时间顺序排列的一列数据。
通过对时间数列的分析,可以了解事件发展的趋势和规律,为预测未来的发展提供参考。
下面将从数列的统计特征、趋势分析和周期性分析三个方面对时间数列进行详细分析。
一、数列的统计特征统计特征是指对时间数列的基本特征进行概括和描述。
常见的数列统计特征包括最大值、最小值、平均值、中位数和标准差等。
最大值是数列中最大的一个数,它反映了事件最高点的出现时间。
最小值是数列中最小的一个数,它反映了事件最低点的出现时间。
平均值是数列中所有数的和除以总数,它反映了事件整体水平的时间变化趋势。
中位数是将数列按大小排列,位于中间位置的数,它反映了事件的中点出现时间。
标准差是用来衡量数列离散程度的指标,它反映了事件的波动程度和不确定性。
通过计算和比较这些统计特征,我们可以对事件发展的整体情况有一个大致的了解。
最大值和最小值可以帮助我们确定事件最高点和最低点的时间范围,平均值可以告诉我们事件发展的平均速度和趋势,中位数可以帮助我们确定事件的中期发展阶段,标准差可以帮助我们评估事件的波动程度和风险。
二、趋势分析趋势分析是指通过时间数列的走势和变化规律,预测事件未来的发展趋势。
常用的趋势分析方法有线性回归分析和移动平均法等。
线性回归分析是一种通过拟合直线来描述事件发展趋势的方法。
它适用于数列具有线性关系的情况,可以通过计算回归方程来预测未来的数值。
线性回归分析的关键是选取合适的变量和确定最佳的拟合直线。
移动平均法是一种通过计算某一时间段内的平均值来描述事件发展趋势的方法。
它适用于数列存在周期性变化的情况,可以抹平季节性波动,更好地反映长期趋势。
移动平均法的关键是选择合适的时间段和计算平均值的方法。
通过趋势分析,我们可以判断事件的增长趋势、下降趋势或者稳定趋势,进而预测事件未来的发展趋势。
趋势分析对于决策制定和未来规划具有重要的参考价值。
三、周期性分析周期性分析是指通过时间数列的周期性变化规律,寻找事件发展的周期性和循环特征。


时间数列分析时间数列分析时间是我们生活中不可或缺的一部分,它们组成了我们的回忆和经历。
时间数列分析是研究时间序列的变化和规律的一种方法。
通过对时间数列进行分析,我们可以了解时间的特性和变化趋势,从而为我们的生活和决策提供有益的信息。
在本文中,我们将详细分析时间数列分析的方法和应用。
时间数列分析是一种数学和统计学的工具,它通过对时间序列进行数学建模和统计分析,揭示时间变量之间的关系和规律。
常见的时间数列分析方法包括趋势分析、周期分析和季节性分析。
首先,趋势分析是指对时间序列数据的长期变化趋势进行分析和预测。
通过观察和分析时间序列的变化趋势,我们可以了解一项事物的增长或下降的速度和方向。
常见的趋势分析方法包括简单移动平均法、指数平滑法和趋势线拟合法。
简单移动平均法是将一段时间内的数据求平均值,作为该时段的预测值。
通过不断滚动窗口,我们可以得到整个时间序列的预测值。
指数平滑法则是通过对历史数据进行加权平均,得到未来的预测值。
这种方法更重视近期的数据,更能反映变化的趋势。
趋势线拟合法则是根据时间序列的变化趋势,拟合出一条线性或非线性曲线,来描述趋势的变化。
周期分析是指对时间序列中的周期性变化进行分析和预测。
周期变化是指在一定时间内重复出现的变化。
对于有明显周期性的数据,周期分析可以帮助我们预测未来的变化趋势。
常见的周期分析方法包括傅里叶分析和自回归移动平均模型(ARMA)。
傅里叶分析是将时间序列数据分解成一系列的频率分量,从而揭示数据的周期性变化。
这种方法可以将复杂的时间序列分解为多个简单的周期波动,进而进行预测和分析。
ARMA模型则是一种统计方法,它结合了自回归(AR)和移动平均(MA)模型,用于预测时间序列的未来值。
通过分析时间序列的自相关性和移动平均性,我们可以建立ARMA模型,进而进行预测。
季节性分析是指对时间序列中的季节性变化进行分析和预测。
季节性变化是指在一年内周期性出现的变化。
对于受季节因素影响较大的数据,季节性分析可以帮助我们了解季节的变化规律,并进行未来的预测。
时间数列时间数列,也称为时间序列或动态序列,是将反映某社会经济现象的指标数值按时间的顺序排列起来所形成的一种统计数列。
它反映社会经济现象发展变化的过程和特点,是研究现象发展变化的趋势和规律以及对未来状态进行科学预测的重要依据。
时间数列的应用始于19世纪80年代西方经济学家和统计学家对资本主义经济周期波动的研究和商情预测。
这种分析的方法技术不断丰富和发展,逐步形成统计学中一个有广泛应用价值的分支系列。
时间数列分析有传统时间数列分析和现代时间数列分析两种。
传统时间数列分析的特点是将经济过程分解为若干基本构成因素、并对这些构成因素分别加以测定。
现代时间数列分析是本世纪40年代开始发展起来的,它把时间数列堪称各种复杂因素交织影响的随机过程,运用大量数据构造综合模型,借助计算机进行复杂的计算,主要用于趋势分析和预测。
本章第一节概述时间数列的种类和编制方法;第二节概述常用的动态分析指标;第三节阐述时间数列的分解测定方法;第五节扼要介绍时间数列在预测中的应用。
第一节:时间数列的种类和编制方法一、时间数列的种类在社会经济统计中,从计算动态指标和预测方法选择来研究,对时间数列可作如下两种分类:1、按指标的形式不同,时间数列可分为绝对数时间数列、相对数时间数列和平均数时间数列。
其中,绝对数时间数列,即总量指标时间数列,又可分为时期总量指标数列(简称时期数列)和时点总量指标数列(简称时点数列)。
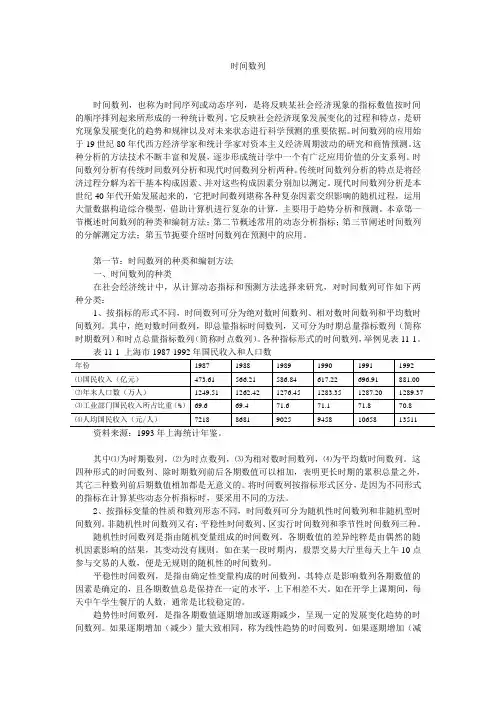
各种指标形式的时间数列,举例见表11-1。
其中⑴为时期数列,⑵为时点数列,⑶为相对数时间数列,⑷为平均数时间数列。
这四种形式的时间数列、除时期数列前后各期数值可以相加,表明更长时期的累积总量之外,其它三种数列前后期数值相加都是无意义的。
将时间数列按指标形式区分,是因为不同形式的指标在计算某些动态分析指标时,要采用不同的方法。
2、按指标变量的性质和数列形态不同,时间数列可分为随机性时间数列和非随机型时间数列。
非随机性时间数列又有:平稳性时间数列、区实行时间数列和季节性时间数列三种。
第9章 时间序列分析课后习题答案第10章(1)30× 31.06×21.05= 30×1.3131 = 39.393(万辆)(2117.11%== (3)设按7.4%的增长速度n 年可翻一番 则有 1.07460/302n==所以 n = log2 / log1.074 = 9.71(年)故能提前0.29年达到翻一番的预定目标。
第11章(1)以1987年为基期,2003年与1987年相比该地区社会商品零售额共增长:%86.2313186.213186.31%)8.61(%)2.81(%)101(555==-=-+⨯+⨯+ (2)年平均增长速度为1%)8.61(%)2.81(%)101(15555-+⨯+⨯+=0.0833=8.33%(3) 2004年的社会商品零售额应为509.52)0833.01(307=+⨯(亿元)第12章 (1)发展总速度%12.259%)81(%)101(%)121(343=+⨯+⨯+平均增长速度=%9892.91%12.25910=-(2)8.561%)61(5002=+⨯(亿元)(3)平均数∑====415.142457041j j y y (亿元),2002年一季度的计划任务:625.1495.142%105=⨯(亿元)。
第13章(1)用每股收益与年份序号回归得^0.3650.193t Y t =+。
预测下一年(第11年)的每股收益为488.211193.0365.0ˆ11=⨯+=Y 元(2)时间数列数据表明该公司股票收益逐年增加,趋势方程也表明平均每年增长0.193元。
是一个较为适合的投资方向。
第14章 (1)移动平均法消除季节变动计算表(2)t T t ⨯+=63995.09625.8上表中,其趋势拟合为直线方程t T t ⨯+=63995.09625.8。
根据上表计算的季节比率,按照公式KL t t t S T Y -⋅=计算可得: 2004年第一季度预测值:7723.21097301.1)1763995.09625.8(ˆˆˆ11717=⨯⨯+=⋅=S T Y2004年第二季度预测值: 49725.23147237.1)1863995.09625.8(ˆˆˆ21818=⨯⨯+=⋅=S T Y2004年第三季度预测值: 009.18852641.0)1963995.09625.8(ˆˆˆ31919=⨯⨯+=⋅=S T Y2004年第四季度预测值:6468.19902822.0)2063995.09625.8(ˆˆˆ42020=⨯⨯+=⋅=S T Y平均法计算季节比率表:季节比率的图形如下:(2)用移动平均法分析其长期趋势原时间序列与移动平均的趋势如下图所示:9.2(1)采用线性趋势方程法:tTi0065.70607.460ˆ+=剔除其长期趋势。
第11章 时间数列分析
一、单项选择题
1、下面四个时间数列中,属于时点数列的是( C )
A 历年招生人数时间数列
B 历年增加在校生人数时间数列
C 历年在校生人数时间数列
D 历年毕业生人数时间数列
2、已知某地区2000年财政收入比1995年增长了1倍,比1990年增长了1.5倍,那么1995年财政收入是1990的( C )
A 0.5倍
B 2.5倍
C 1.25倍
D 1.5倍
3、已知一个数列的环比增长速度分别为3%,5%,8%,则该数列的定基增长速度为( D )
A 3%⨯5%⨯8%
B 103%⨯105%⨯108%
C (3%⨯5%⨯8%)+1
D (103%⨯105%⨯108% )-1
4、某地区1975年粮食亩产350公斤,2000年亩产为600公斤,求1976年至2000年的粮食亩产的平均增长速度应开( B )方。
A 24次
B 25次
C 26次
D 23次
5、某地1980年工农业总产值为6800万元,计划以后每年按6%的增长速度增长,到2000年年末的工农业总产值为( A )
A 21808.5万元
B 144160万元
C 8160万元
D 7208万元
6、某地区粮食产量的环比增长速度,1998年为3%,1999年为5%,则1998~1999年该地区的粮食产量共增长了( C )
A 2%
B 8%
C 8.15%
D 15%
7、某地1995-2000年的国内生产总值分别为800、860、900、950、1100、1500万元,则国内生产总值平均每年增长量为( B )
A 116.7万元
B 140.0万元
C 128.0万元
D 120.0万元
8、某企业销售额1993-1995年三年间的平均发展速度为106%,1996-2000年五年间的平均发展速度为108%,则八年间的平均发展速度为( B ) A
08.106.1⨯ B 85308.106.1⨯ C 808.106.1⨯ D 5308.106.1⨯
9、已知某企业总产值1992年比1989年增长87.5%,1991年比1989年增长50%,则1992年比1991年增长( B )。
A 、37.5%
B 、25%
C 、15%
D 、68.75%
10、发展速度属于( C )
A 比例相对数
B 比较相对数
C 动态相对数
D 强度相对数
11、采用几何平均法计算平均发展速度的依据是( A )
A 各年环比发展速度之积等于总速度
B 各年环比发展速度之和等于总速度
C 各年环比增长速度之积等于总速度
D 各年环比增长速度之和等于总速度 12、定基发展速度和环比发展速度的关系是( A )。
A 、 两个相邻时期的定基发展速度之商等于相应的环比发展速度
B 、 两个相邻时期的定基发展速度之差等于相应的环比发展速度
C 、 两个相邻时期的定基发展速度之和等于相应的环比发展速度
D 、 两个相邻时期的定基发展速度之积等于相应的环比发展速度
13、把某企业在十年间拥有的生产设备台数,按时间顺序排成数列,则这个数列是( B )。
A. 时期数列
B. 时点数列
C. 变量数列
D. 分布数列
14、下列说法正确的有( BC )
A 平均增长速度大于平均发展速度
B 平均增长速度小于平均发展速度
C 平均增长速度=平均发展速度-1
D 平均发展速度=平均增长速度-1
E 平均发展速度×平均增长速度=1
15、下列计算增长速度的公式正确的有( ACD )
A 增长速度=%100⨯基期水平增长量
B 增长速度= %100⨯报告期水平
增长量 C 增长速度= 发展速度—100%
D 增长速度=%100⨯-基期水平
基期水平报告期水平 E 增长速度= %100⨯基期水平
报告期水平
A 第二年的环比增长速度=定基增长速度=10%
B 第三年的累计增长量=逐期增长量=200万元
C 第四年的定基发展速度为135%
D 第五年增长1%绝对值为14万元
E 第五年增长1%绝对值为13.5万元
17、测定长期趋势的方法主要有( AD )
A 时距扩大法
B 方程法
C 最小平方法
D 移动平均法
E 几何平均法
18.移动平均法的主要作用在于( A )。
A 、消弱短期的偶然因素引起的波动
B 、削弱长期的基本因素引起的波动
C 、削弱短期的基本因素引起的波动
D 、消除季节变动
二、多项选择题
1、一个时间数列的基本要素包括( CD )
A 变量
B 次数
C 现象所属的时间
D 现象所属的地点
E 反映现象的统计指标值
2、按统计指标表现形式不同,时间数列可以分为( ABC )
A 绝对数时间数列
B 相对数时间数列
C 平均数时间数列
D 时期数列
E 时点数列
3、增长百分之一的水平值是(ACE )
A 表示每增加一个百分点所增加的绝对量
B 表示每增加一个百分点所增加的相对量
C 等于前期水平除以100
D 等于前期水平除以100%
E 等于环比增长量除以环比增长速度
4、定基增长速度等于(AD )
A 定基发展速度减1
B 环比发展速度的连乘积
C 环比增长速度的连乘积
D 环比增长速度加1后连乘积再减1
E 定基增长量除以基期水平。