第五章时间数列(动态)分析 答案

第五章思考题参考答案1．什么是总量指标？它在统计工作中有何重要作用？答：总量指标是反映社会经济现象总体在一定时间、地点、条件下的总规模、总水平或工作总量的统计指标。

总量指标是认识社会经济现象的起点；总量指标是进行经济管理的主要依据；总量指标是基础性指标。

2．总体单位总量和总体标志总量有什么区别？答：总体单位总量指总体单位数之和，即总体本身的规模大小。

总体标志总量是指总体各单位就某一数量标志的标志值之和。

总体单位总量与总体标志总量的相对性。

一个总量指标究竟属于总体单位总量还是总体标志总量，应该随着研究目的不同和研究对象的变化而定。

3．时期指标和时点指标如何区分？答：不同时期指标数值可以累计相加，各个时点指标不具有累加性，也就是说数值相加没有意义；时期指标数值的大小与其计算时期长短有直接关系，时点指标的大小与登记时间间隔长短没有直接关系；时期指标的数值需要连续登记取得，时点指标的数值一般是间断统计取得的。

4．什么是实物指标?有什么作用？答：实物单位是根据事物的自然属性和特点而规定的计量单位。

实物指标是反映国情、国力和研究各行业投入、产出、资源条件、生活环境、经济活动过程等基础的指标。

它能具体反映社会经济现象实际存在的实物数量，体现具体的使用价值量。

5．什么是价值指标？有什么作用？答：以货币作为价值尺度来计量社会物质财富和劳动成果的计量单位。

以货币单位来度量事物的数量，使不能直接相加的经济现象的数量过渡到可以加总，用以综合地说明具有不同使用价值的经济现象的总规模、总水平和总速度。

由于价值指标具有广泛的综合性，所以它在统计核算有广泛的使用途径。

6．计算总量指标有哪些要求？答：明确总量指标的涵义、计算范围；注意总量指标计算时现象的同质性；要有统一的计量单位。

第六章 相思考题参考答案1．什么是相对指标？它有哪几种表现形式？有什么作用？答：相对指标又称相对数，它是将两个有联系的统计指标数值对比求得的比值，是用来反映现象的发展程度、结构、强度、普通程度或比例关系。

初级统计师《统计专业知识和实务》章节练习题：第五章时间数列含答案一、单项选择题1.根据时期指标时间数列，计算平均发展水平采用()。

A.加权算术平均法B.首末折半法C.简单算术平均法D.几何平均法【答案】C2.评比城市间的社会发展状况，将各城市每人分摊的绿化面积按年排列的时间数列是属于()。

A.时期数列B.时点数列C.相对指标时间数列D.平均指标时间数列【答案】C【解析】相对指标时间数列是指将同一相对指标的数值按其发生的时间先后顺序排列而成的数列。

题中，平均每人分摊绿化面积是一个强度相对指标，将其按年排列的时间数列属于相对指标时间数列。

3.下列对时点数列特征的描述，错误的一项是()。

A.时点数列中的指标数值可以相加B.时点数列中指标数值的大小与计算时间间隔长短无关C.时点数列中各指标数值的取得，是通过一次性调查登记而来的D.时点数列属于总量指标时间数列【答案】A【解析】A项，时点数列中的指标数值不能相加，相加没有意义。

4.下列数列中属于时间数列的是()A.学生按学习成绩分组形成的数列B.工业企业按地区分组形成的数列C.职工按工资水平高低排列形成的数列D.出口额按时间先后顺序排列形成的数列【答案】D【解析】时间数列是指将同一统计指标在不同时间上的数值，按时间先后顺序排列而形成的数列。

题中，A、B、C项均不是按照时间顺序排列，故不属于时间数列，属于统计分组。

5.根据间隔相等的间断时点数列，计算序时平均数应采用()。

A.几何平均法B.加权算术平均法C.简单算术平均法D.首末折半法【答案】D【解析】间隔相等的间断时点数列计算序时平均数应采用首末折半法，其计算公式为：6.设(甲)代表时期数列;(乙)代表时点数列;(丙)代表加权算术平均数;(丁)代表“首末折半法”序时平均数。

现已知2005～2009年某银行的年末存款余额，要求计算各年平均存款余额，则该数列属于______，应采用的计算方法是______。

()A.甲;丙B.乙;丙C.甲;乙D.乙;丁【答案】D【解析】当时间数列中所包含的总量指标都是反映社会经济现象在某一瞬间上所达到的水平时，这种总量指标时间数列就称为时点数列。

第五章时间数列一、单项选择题(以下每小题各有四项备选答案，其中只有一项是正确的)1．下列数列中属于时间数列的是( )A．学生按学习成绩分组形成的数列B．工业企业按地区分组形成的数列C．职工按工资水平高低排列形成的数列D．出口额按时间先后顺序排列形成的数列[答案] D[解析] 时间数列是指将同一统计指标在不同时间上的数值，按时间先后顺序排列而形成的数列。

题中，A、B、C项均不是按照时间顺序排列，故不属于时间数列，属于统计分组。

2．评比城市间的社会发展状况，将各城市每人分摊的绿化面积按年排列的时间数列是属于( )。

A．时期数列 B．时点数列C．相对指标时间数列 D．平均指标时间数列[答案] C[解析] 相对指标时间数列是指将同一相对指标的数值按其发生的时间先后顺序排列而成的数列。

题中，平均每人分摊绿化面积是一个强度相对指标，将其按年排列的时间数列属于相对指标时间数列。

3．已知某商业集团2008-2009年各季度销售资料，如表5-1所示。

表5-1则表5-1中，属于时期数列的有( )。

A．1、2、3 B．1、3、4 C．2、4 D．1、3[答案] D[解析] 1、3的每个数值反映的是现象在一段时期内发展过程的绝对数之和，故属于时期指标数列；2的每个数值反映的是现象在某一时间上所达到的绝对水平，故属于时点指标数列；4是把同一相对指标在不同时间上的数值按时间先后顺序排列而形成的数列，故属于相对指标数列。

4．下列对时点数列特征的描述，错误的一项是( )。

A．时点数列中的指标数值可以相加B．时点数列中指标数值的大小与计算时间间隔长短无关C．时点数列中各指标数值的取得，是通过一次性调查登记而来的D．时点数列属于总量指标时间数列[答案] A[解析] A项，时点数列中的指标数值不能相加，相加没有意义。

5．根据时期指标时间数列，计算平均发展水平采用( )。

A．加权算术平均法 B．首末折半法C．简单算术平均法 D．几何平均法[答案] C[解析] 根据时期数列计算序时平均数，可以采用简单算术平均数，将各时期指标数值的总和除以发展水平值个数，其公式为：6．根据间隔相等的间断时点数列，计算序时平均数应采用( )。

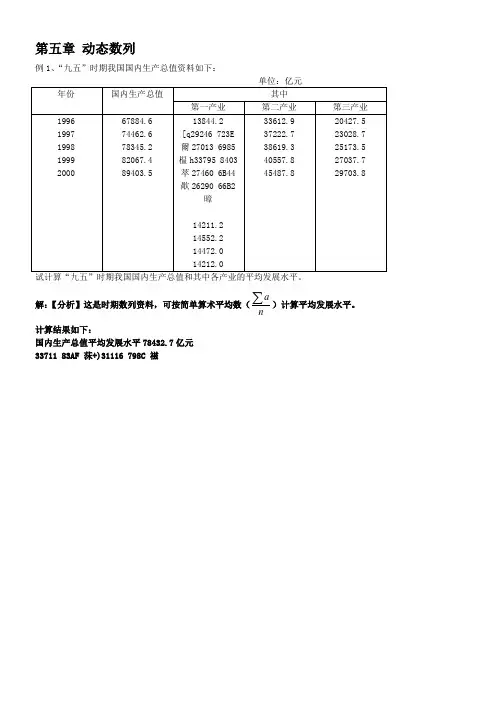
第五章动态数列例1、“九五”时期我国国内生产总值资料如下：单位：亿元解：【分析】这是时期数列资料，可按简单算术平均数（n a）计算平均发展水平。

计算结果如下：国内生产总值平均发展水平78432.7亿元33711 83AF 莯+)31116 798C 禌22548 5814 堔23888 5D50 嵐35943 8C67 豧其中：第一产业平均发展水平14258.3亿元；第二产业平均发展水平39100.1亿元；第三产业平均发展水平25074.2亿元。

例2、我国人口自然增长情况见下表：试计算我国在“七五”时期年平均增加人口数量。

解：【分析】新增长人口是时期指标，故平均增加人口数量仍用na a ∑=计算。

年平均增加4.1696516291678172617931656=++++==∑na a （万人）例3、某商店2010年商品库存资料如下：30139 75BB 疻\22102 5656 噖36028 8CBC 貼j20316 4F5C 作$试计算第一季度、第二季度、上半年、下半年和全年的平均库存额。

解：这是一个等间隔时点数列，用“首末折半法”计算：试计算2002年该企业平均工人数。

解：【分析】这是不等间隔时点数列，用间隔月数进行加权的公式计算平均工人数：12111232121)(21)(21)(21---+++++++++=n n n n f f f f a a f a a f a a a 133221124124123241241432414408224083352233533012330326+++++⨯++⨯++⨯++⨯++⨯++⨯+==385（人） 例5、某企业2002年各季度计划利润和利润计划完成程度的资料如下：试计算该企业年度利润计划平均完成百分比。

解：【分析】应该按两个时期数列对比组成的相对指标动态数列计算序时平均数的算式计算： 该企业利润年平均计划完成百分比（%）%132898875887860%125898%138875%135887%130860=+++⨯+⨯+⨯+⨯=例6、1995-2000年各年底某企业职工工人数和工程技术人员数资料如下：解：【分析】这是由两个时点数列对比所组成的相对指标动态数列计算序时平均数的问题。

《统计学概论》第五章课后练习题答案一、思考题1．什么叫时间序列，构成时间序列的基本要素有哪些？P1212．序时平均数与一般平均数有何异同？P1273．时间数列与时点数列有哪些区别？P124－1254．环比增长速度与定基增长速度之间有什么关系？P1365．什么是平均发展速度？说说水平法和累计法计算平均发展速度的基本思路，各在什么情况下选用？P1386．测定长期趋势有哪些常用的方法？测定的目的是什么？P1367．实际中如何根据时间序列的发展变化的数列特征来判断合适的趋势方程形式？P145 8．影响时间序列指标数值大小的因素有哪些？这些因素共同作用的理论模型有哪些？P140二、判断题1．时间序列也称动态数列，它是变量数列的一种形式。

（ × ）【解析】时间序列是数列，而变量数列是静态数列。

2．时间数列和时点数列属于总量指标时间序列。

（√）3．所谓序时平均数是指将同一总体的不同时期的平均数按时间先后顺序排列起来。

（× ）【解析】序时平均数是将不同时期的发展水平加以平均而得到的平均数。

4．间隔相等的时期数列计算平均发展水平时，应用首末折半法。

（ × ）【解析】间隔相等的时点数列计算平均发展水平时，应用首末折半法。

5．平均增长速度等于各期环比增长速度连乘积开n次方。

（× ）【解析】平均发展速度等于各期环比发展速度连乘积开n次方，平均增长速度=平均发展速度－1（或100%）6．两个相邻时期的定基发展速度之比等于相应的环比发展速度。

（√）7．用移动平均法测定长期趋势时，移动平均项数越多越好。

（ × ）【解析】移动平均法所取项数的多少，应视资料的特点而定。

8．某一时间序列有25年的数据，若采用五项移动平均，则修匀后的数列缺少4项数据。

（√）9．如果时间序列是年度数据，则不存在季节变动。

（√）10．用相同方法拟合趋势方程时，t的取值不同，则得到的趋势方程也不同，但趋势预测值不变。

第五章时间数列一、单项选择题：1. 动态数列的构成要素是（）。

A、变量和次数B、时间和指标数值C、时间和次数D、主词和宾词2. 动态数列中，每个指标数值可以直接相加的是（）。

A、相对数数列B、时期数列C、间断时点数列D、平均数数列3. 按季平均法测定季节比例时，各季的季节比率之和应等于（）。

A、100%B、400%C、120%D、1200%4. 按月平均法测定季节比率时，各月的季节比率之和应等于（）。

A、100%B、400%C、120%D、1200%5. 定基增长速度与环比增长速度的关系为（）。

A、定基增长速度等于相应的环比增长速度各个的算术和B、定基增长速度等于相应的环比增长速度各个的连乘积C、定基增长速度等于相应的环比增长速度加1后的连乘积再减1D、定基增长速度等于相应的环比增长速度各个的连乘积加16. 以1950年钢产量为最初水平，2007年钢产量为最末水平，计算钢产量的年 平均发展速度时，须开（ ）次方。

A 、56B 、57C 、58D 、597. 某地从2002—2007年各年12月31日统计的人口资料如下：则该地区2003—2007年的平均人数为（ ）。

（万人）、3.24522625252423223=+++++A （万人）、6.2452625252423=++++B （万人）、7.195226252524223=++++C （万人）、25.20622625252423223=+++++D8. 平均发展速度是各期（）的平均数。

A、发展水平B、环比增长速度C、环比发展速度D、定基发展速度9. 在具有各期的环比发展速度的情况下，各期环比发展速度的连乘积等于（）。

A、平均发展速度B、总增长速度C、定基增长速度D、定基发展速度10、时间序列在一年内重复出现的周期性波动称为（）A、长期趋势B、季节变动C、循环变动D、随机变动11、增长一个百分点而增加的绝对数量称为（）A、环比增长速度B、平均增长速度C、年度增长速度D、增长1%绝对值12、在使用指数平滑法进行预测时，如果时间序列比较平稳，则平滑系数α的取值（）A 、应该小些B 、应该大些C 、等于0D 、等于113、对某一时间序列拟合的直线趋势方程为bt a y t +=∧，如果该数列中没有明显的长期趋势，则b 的值应该（ ）A 、接近1B 、小于1C 、接近0D 、小于0 14、某银行投资额2004年比2003年增长了10%，2005年比2003年增长了15%，2005年比2004年增长了（ ）A 、15%÷10%B 、115%÷110%C 、（110%×115%）+1D 、（115%÷110%）-1 15、某种股票的价格周二上涨了10%，周三上涨了5%，两天累计涨涨幅达（）A 、15%B 、15.5%C 、4.8%D 、5%16、某市近五年各年T 恤衫销售量大体持平，年平均为1200万件，7月份的季节比率为220%，8月份月平均销售量比7月份低45%，正常情况下8月份的销售量应该是（ ）A 、1452万件B 、121万件C 、220万件D 、99万件二、多项选择题：1. 用于分析现象发展水平的指标有（ ）A 、发展速度B 、发展水平C 、增长量D 、增长速度E 、平均增长量2. 序时平均数是（ ）A 、平均发展水平B 、平均发展速度C 、平均增长速度D 、动态平均数E 、平均增长量3. 应用最小平方法配合一条理想的趋势线要求满足的条件是（ ）4. 时点数列的特点有（ ）。

A. 140 万元B.150 万元6. 下列指标中属于时点指标的是 （ A ） A. 商品库存量 C .平均每人销售额7. 时间数列中，各项指标数值可以相加的是 A. 时期数列 C. 平均数时间数列8. 时期数列中各项指标数值（ A ） A. 可以相加C .绝大部分可以相加10.某校学生人数 2005年比 2004年增长了8%，2006年比 2005年增长了 15%，2007年比 2006 年增长了 18%，则 2004-2007 年学生人数共增长了（ D ）（ 2008年 10月）A.8 % +15% +18%B.8 %X 15%X 18%C. （ 108% +115% +118%） -1D.108%X 115%X 118%-1二、多项选择题1. 将不同时期的发展水平加以平均而得到的平均数称为 （ ABD ） （2012年1月）A.序时平均数B.动态平均数C.静态平均数D.平均发展水平E. 一般平均数2. 定基发展速度和环比发展速度的关系是 （ BD ） （2011年 10月） A. 相邻两个环比发展速度之商等于相应的定基发展速度、单项选择题 第五章 时间序列分析1. 构成时间数列的两个基本要素是 （ A.主词和宾词 ） （2012年 1月）B. 变量和次数 C .现象所属的时间及其统计指标数值 2．某地区历年出生人口数是一个 （ A.时期数列 D.时间和次数2011年 10 月）B. 时点数列 C .分配数列 D .平均数数列3. 某商场销售洗衣机， 2008 年共销售 （2010年 10） A. 时期指标 C. 前者是时期指标，后者是时点指标4. 累计增长量 （ A ） （ 2010年 10） A. 等于逐期增长量之和 C.等于逐期增长量之差5. 某企业银行存款余额 4 月初为 80 万元， 6000 台，年底库存 50 台，这两个指标是 （ C ）B. 时点指标D. 前者是时点指标，后者是时期指标B. 等于逐期增长量之积 D •与逐期增长量没有关系160 万元，则该企业第二季度的平均存款余额为（5 月初为 150 万元，6 月初为 210 万元，7 月初为C ）（ 2009年 10）C.160 万元 D .170万元（ 2009年 10） B. 商品销售量 D .商品销售额 （ A ）（2009年10）B.相对数时间数列 D. 时点数列2009年1月）B. 不可以相加D. 绝大部分不可以相加B. 环比发展速度的连乘积等于定基发展速度C. 定基发展速度的连乘积等于环比发展速度D .相邻两个定基发展速度之商等于相应的环比发展速度E.以上都对3. 常用的测定与分析长期趋势的方法有A. 时距扩大法（ ABC ）（2011年1 月）B.移动平均法C. 最小平方法4. 时点数列的特点有（ BCD ）A. 数列中各个指标数值可以相加D.几何平均法2010年10）E. 首末折半法B. 数列中各个指标数值不具有可加性C. 指标数值是通过一次登记取得的D. 指标数值的大小与时期长短没有直接的联系E. 指标数值是通过连续不断的登记取得的5.增长1%的绝对值等于（AC ）（2010年1）A.增加一个百分点所增加的绝对量B. 增加一个百分点所增加的相对量C .前期水平除以100 D. 后期水平乘以1% E .环比增长量除以100再除以环比发展速度6. 计算平均发展速度常用的方法有（ A.几何平均法（水平法） C•方程式法（累计法）E.加权算术平均法7. 增长速度（ADEA. 等于增长量与基期水平之比C.累计增长量与前一期水平之比AC ）（2009年10）B.调和平均法D.简单算术平均法）（2009年1 月）B. 逐期增长量与报告期水平之比D. 等于发展速度-1E .包括环比增长速度和定基增长速度8. 序时平均数是（CE ）A.反映总体各单位标志值的一般水平2008年10月）B.根据同一时期标志总量和单位总量计算C•说明某一现象的数值在不同时间上的一般水平D. 由变量数列计算E. 由动态数列计算三、判断题1. 职工人数、产量、产值、商品库存额、工资总额指标都属于时点指标。

第五章时间数列分析一、单项选择题1、时间数列就是( )①将一系列统计指标排列起来而形成②将同类指标排列起来而形成③将同一空间、不同时间得统计指标数值按时间先后顺序排列起来而形成④将同一时间、不同空间得统计指标数值排列起来而形成2、下列属于时点数列得就是( )①某地历年工业增加值②某地历年工业劳动生产率③某地历年工业企业职工人数④某地历年工业产品进出口总额3、时间数列中,各项指标数值可以相加得就是( )①绝对数时间数列②时期数列③时点数列④相对数或平均数时间数列4、时间数列中得发展水平( )①只能就是绝对数②只能就是相对数③只能就是平均数④可以就是绝对数,也可以就是相对数或平均数5、发展速度与增长速度得关系就是( )①环比发展速度=定基发展速度-1 ②增长速度=发展速度-1③定基增长速度得连乘积等于定基发展速度④环比增长速度得连乘积等于环比发展速度6、在实际工作中计算同比发展速度就是因为( )①资料易于取得②消除季节变动得影响③消除长期趋势得影响④方便计算7、某地国内生产总值2005年比2000年增长53、5%,2004年比2000年增长40、2%,则2005年比2004年增长( )①9、5% ②13、3%③33、08% ④无法确定8、某企业第一季度三个月份得实际产量分别为500件、612件与832件,分别超计划0%、2%与4%,则该厂第一季度平均超额完成计划得百分数为( )①102% ②2%③2、3% ④102、3%9、某网站四月份、五月份、六月份、七月份平均员工人数分别为84人、72人、84人、96人,则第二季度该网站得月平均员工人数为( )①84 人②80人③82 人④83人10、几何平均法平均发展速度数值得大小( )①不受最初水平与最末水平得影响②只受中间各期水平得影响③只受最初水平与最末水平得影响④既受最初水平与最末水平得影响,也受中间各期水平得影响11、累计法平均发展速度得实质( )①从最初水平出发,按平均增长量增长,经过n期正好达到第n期得实际水平②从最初水平出发,按平均发展速度发展,经过n期正好达到第n期得实际水平③从最初水平出发,按平均发展速度计算得到得各期理论水平之与正好等于各期得实际水平之与④从最初水平出发,按平均发展速度计算得到得各期理论水平之与正好等于最末期得实际水平12、已知某地1996—2000年年均增长速度为10%,2001—2005年年均增长速度为8%,则这10年间得平均增长速度为( )①1008.01.0⨯②1081.110-⨯③()()105508.01.0⨯④()()108.11.11055-⨯13、直线趋势方程bxay+=ˆ中,ba和得意义就是( )①a表示直线得截距,b表示0=x时得趋势值②a表示最初发展水平得趋势值,b表示平均发展速度③a表示最初发展水平得趋势值,b表示平均发展水平④a就是直线得截距,表示最初发展水平得趋势值;b就是直线得斜率,表示平均增长量14、若动态数列得逐期增长量大体相等,宜拟合( )①直线趋势方程②曲线趋势方程③指数趋势方程④二次曲线方程15、假定被研究现象基本上按不变得发展速度发展,为描述现象变动得趋势,借以进行预测,应拟合得方程就是( )①直线趋势方程②曲线趋势方程③指数趋势方程④二次曲线方程16、若动态数列得二级增长量大体相等,宜拟合( )①直线趋势方程②曲线趋势方程③指数趋势方程④二次曲线方程17、移动平均法得主要作用就是( )①削弱短期得偶然因素引起得波动②削弱长期得基本因素引起得波动③消除季节变动得影响④预测未来18、按季平均法测定季节比率时,各季得季节比率之与应等于( )①100% ②400%③120% ④1200%19、已知时间数列有30年得数据,采用移动平均法测定原时间数列得长期趋势,若采用5年移动平均,修匀后得时间数列有( )得数据？①30年②28年③25年④26年20、序时平均数中得“首尾折半法”适用于计算( )①时期数列得资料②间隔相等得间断时点数列得资料③间隔不等得间断时点数列得资料④由两个时期数列构成得相对数时间数列资料21、下列动态数列分析指标中,不取负值得就是( )①增长量②发展速度③增长速度④平均增长速度22、说明现象在较长时期内发展总速度得指标就是( )①环比发展速度②平均发展速度③定基发展速度④定基增长速度二、多项选择题1、编制时间数列得原则( )①时间长短要统一②总体范围要一致③指标得经济内容要统一④指标得计算方法要一致⑤指标得计算价格与计量单位要统一2、时点数列中( )①各个时点得指标数值连续累加有实际得经济意义②各个时点得指标数值连续累加没有实际得经济意义③各个时点得指标数值一般靠一次性得调查登记取得④各个时点得指标数值一般靠经常性得调查登记取得⑤各个时点指标数值得大小与其对应时点得间隔长短没有直接关系3、下列属于时期数列得有( )①河南省历年出生得婴儿数②河南省历年年末人数③河南省历年固定资产投资额④河南省历年固定资产原值⑤河南省历年国内生产总值4、将不同时期得发展水平加以平均而得到得平均数称为( )①序时平均数②动态平均数③静态平均数④平均发展水平⑤一般平均数5、序时平均数与静态平均数得主要区别就是( )①计算时所依据得资料不同②抽象掉得差异不同③反映得一般水平不同④动态平均数不就是平均指标,而静态平均数就是平均指标⑤动态平均数根据时间数列计算,静态平均数根据分布数列计算6、分析时间数列得水平指标有( )①发展水平②发展速度③增长量④平均发展水平⑤平均增长量7、用公式n aa∑=计算平均发展水平适用于下面哪些情况得时间数列( )①时期相等得时期数列②时点数列③间断得时点数列④连续得时点数列⑤间隔相等得连续时点数列8、增长速度与发展速度得关系( )①两者仅相差一个基数②发展速度=增长速度+1③增长速度等于各环比增长速度得连乘积④定基增长速度=定基发展速度-1⑤定基增长速度=各环比发展速度得连乘积-19、若两个相邻时期得环比发展速度皆为106%,则( )①这两个时期得逐期增长量相等②这两个时期得定基发展速度相等③这两个时期得发展水平相等④这两个时期得环比增长速度相等⑤这两个时期得平均发展速度为106%10、计算平均发展速度得几何平均法与方程式法得区别( )①理论依据不同②侧重点不同③适用范围不同④用几何平均法计算得平均发展速度,可以保证用这一速度推算出得最末一期得理论水平与其实际水平相等,而方程式法则不能⑤用方程式法计算得平均发展速度,可以保证用这一速度推算出得最末一期得理论水平与其实际水平相等,而几何平均法则不能11、计算与应用平均速度指标应注意( )①根据研究问题得目得与研究对象得特点,合理选择计算方法②基期得选择要适当③用几何平均法计算平均速度时,要特别关注特殊时期环比速度得变动情况④用分段平均速度补充说明总得平均速度⑤平均速度还应与时间数列中得其它分析指标相结合12、影响社会经济现象发展变化得因素主要有( )①基本因素②偶然因素③季节因素④变量值水平⑤权数大小13、测定长期趋势得意义( )①测定长期趋势得走向,以便认识与掌握现象发展变化得规律性②利用现象发展得长期趋势,可对未来得情况做出预测③对时间数列进行修匀④拟合趋势线⑤测定长期趋势,还可以将长期趋势从时间数列中分离出来,以便更好得研究季节变动与循环变动14、计算移动平均数时,采用得项数( )①可以就是奇数项②可以就是偶数项③一般多用奇数项④一般多用偶数项⑤奇数项与偶数项并用15、应用移动平均法测定长期趋势时,采用多少项计算移动平均数,一般应考虑( )①现象得变化就是否有周期性②原数列项数得多少③原数列得变化趋势④就是否需要移动平均数数列得首尾数值⑤就是时期数列还就是时点数列16、用按季或按月平均法测定季节变动( )①方法简便②在原数列不存在明显长期趋势时采用③在原数列存在明显长期趋势时采用④计算出得季节比率比长期趋势剔除法准确⑤计算出来得季节比率不能说明任何问题17、最小平方法测定长期趋势得数学依据就是( )①)ˆ(2=-∑yy②)ˆ(=-∑yy③=-∑2)ˆ(yy最小值④=-∑)ˆ(yy最小值⑤)ˆ(2<-∑yy三、填空题1、时间数列一般由两个基本要素构成:一就是( );二就是( )。

五：时间数列和动态分析一、填空题1、时间数列是将总体某一个在不同时间上的指标值，按先后顺序排列而成。

2、时间数列由两个要素构成：一个是指标值所属的；另一个是各时间上的。

3、平均发展速度是的序时平均数，它有和两种计算方法。

4、测定长期趋势的常用方法有法、法、法和法。

5、动态数列的分析指标可以分为和两大类。

6、动态数列的水平指标有、、和等。

7、动态数列的速度指标有、、和等。

8、由间隔相等的间断时点数列计算序时平均数时应用法，由间隔不等的间断时点数列计算序时平均数时应用法。

9、根据某20项的时间数列，采用五项移动平均法进行修匀，修匀后的新的时间数列有项。

10、发展速度根据基期选择的不同可分为和，两者之间具有的数量关系。

11、增长量指标由于采用不同的基期可分为和，两者之间具有的数量关系。

12、在移动平均法方法下，移动平均的项数越长，数列所表现的长期趋势。

13、时间数列的影响因素可分解为、、和。

14、时间数列中的大体相等时，可配合直线方程；大体相等时，可配合抛物线方程。

15、半数平均法的数学根据是；最小平方法的数学依据是。

二、是非题1、将总体系列不同的综合指标排列起来就构成时间数列。

2、用几何法计算的平均发展速度的大小，与中间各期水平的大小无关。

3、编制时点数列，各项指标的间隔长短必须保持一致。

4、用水平法计算的平均速度，实质上只反映了现象首末水平的变化。

5、对于同一资料，按水平法和方程法计算的平均发展速度是相等的。

6、用方程法计算的平均发展速度的大小取决于各期发展水平总和的大小。

7、半数平均法的数学依据是变量的实际值与理论值的离差平方和为最小。

8、通过时间数列前后各时间上指标值的对比，可以反映现象的发展变化过程及其规律。

9、时期数列中每个指标值的大小和它所对应时期的长短有直接关系。

10、时点数列中各个时点的指标值可以相加。

11、定基发展速度等于相应时期内各个环比发展速度的连乘积。

12、间隔相等的间断时点数列序时平均数的计算采用“首尾折半简单算术平均法”13、事物的发展变化是多种因素共同作用的结果，其中长期趋势是根本的因素，反映现象的变动趋势。