初二数学入学测试题

八年级下学期数学入学测试卷（考试时间：90分钟，试卷满分120分）一、选择题（本大题10小题，每小题3分，共30分）1.以下绿色食品、回收、节能、节水四个标志中，是轴对称图形的是（ ）A..B..C..D..2.下列每组数据中，能作为三角形三边边长的是( ) A.3、4、8 B.8、7、15C.5、5、11D.13、12、203.分式32-x y 有意义的条件是( )A.x 0B.y 0C.x 3D.x -34.如图，1=2，AB=AD ，则ABC ≌ADC ，采用的判定方法是( )A.SSSB.SASC.ASAD.AAS5.下列分解因式正确的是( ) A.﹣a+a 3＝﹣a(1+a 2)B.2a ﹣4b+2＝2(a ﹣2b)C.a 2﹣4＝(a ﹣2)2 D.a 2﹣2a+1＝(a ﹣1)26.等腰三角形的一个角为，则顶角为( )A.040B.0100C.040或0100D.0707.下列运算中，正确的是（ ） A.4m ﹣m ＝3 B.(﹣m 3n)3＝﹣m 6n 3C.m 6m 3＝m 2D.(m ﹣3)(m+2)＝m 2﹣m ﹣68.如图，ABC 中，A=，ABC 的两条角平分线交于点P ，BPD 的度数是( ) A.B.C.D.9.如图，Rt ABC 中，C=，AD 平分BAC ，交BC 于点D ，AB=10，S ABD =15，则CD 的长为( ) A.3 B.4 C.5 D.610.一件工作，甲单独做a 小时完成，乙单独做b 小时完成，则甲、乙两人合作完成需要（ ）小时。

A.b a11+B.ab 1C.ba +1D.ba ab +二、填空题（每题4分，共28分） 11.约分的结果是________．12.已知3x ＝5，3y ＝2，则3x+y 的值是_______．13. 已知m+n=-6，mn=4，则m 2-mn+n 2的值为_______． 14. 一个n 边形的内角和等于0720，则n ＝_______． 15. 如图，ABC ≌ADE ，若C ＝，D ＝，DAC ＝，则BAD ＝_______．16.如图，在ABC 中，ACB ＝，CD 是AB 边上的高，A ＝，AB ＝20，则BD ＝_______．（15题图） （ 16题图） （17题图）17.如图，已知ABC 中，AC ＝AB=5，BC ＝3，DE 垂直平分AB ，点D 为垂足，交AC 于点 E ．那么EBC 的周长为_______．三、解答题（一）（本大题3小题，每小题6分，共18分）18．计算：()()()()33442x y x y x y xy xy +---÷19．如图，AB=AC ，AD=AE ，∠BAC=∠DAE ．求证：BE=CD ．20．已知，如图，在△ABC中，AD，AE分别是△ABC的高和角平分线，若∠B=35°，∠C=65°．求∠DAE 的度数．四、解答题（二）（本大题3小题，每小题8分，共24分）21．ABC在平面直角坐标系中的位置如图所示，A、B、C三点在格点上22．今年新冠肺炎疫情在全球肆虐，为降低病亡率，某工厂平均每天比原计划多生产10台呼吸机，现在生产120台呼吸机的时间与原计划生产90台呼吸机所需时间相同．求该工厂原来平均每天生产多少台呼吸机？23.已知，如图，AB=AC，BD=CD，DE⊥AB于点E，DF⊥AC于点F，求证：（1）AD平分∠BAC．（2）DF=DE五、解答题（三）（本大题2小题，每小题10分，共20分）24.请认真观察图形，解答下列问题：（1）根据图中条件，试用两种不同方法表示阴影部分的面积．方法1：；方法2：．（2）从中你能发现什么结论？请用乘法公式表示该结论：．（3）运用你所得到的结论，解决问题：已知6,25)2==+xyyx（求22x y+的值．25.如图，△ABC和△ADE都是等腰三角形，BC、DE分别是这两个等腰三角形的底边，且∠BAC=∠DAE．（1）求证：BD=CE；（2）连接DC．如果CD=CE，试说明直线AD垂直平分线段BC．（1）作出ABC关于x轴对称的111A B C△，并写出点1A，1B，1C 的坐标；（2）在y轴上找点D，使得AD BD+最小。

一、选择题（每题3分，共30分）1. 下列各数中，有理数是（）A. √9B. √-16C. πD. √22. 已知a > 0，b < 0，那么下列各式中，正确的是（）A. a + b > 0B. a - b > 0C. a - b < 0D. a + b < 03. 下列各式中，同类项是（）A. 2x^2y 和 3xy^2B. 4a^3 和 2a^2C. 5mn 和 3m^2nD. 6x^2 和 -3x^24. 已知x^2 - 5x + 6 = 0，那么x的值为（）A. 2 或 3B. 1 或 4C. 1 或 6D. 2 或 65. 下列各式中，完全平方公式适用的是（）A. (a + b)^2B. (a - b)^2C. (a + b)(a - b)D. (a + b)(a + b)6. 下列各数中，绝对值最小的是（）A. -5B. -4C. 0D. 37. 下列各式中，分式有意义的是（）A. 2x / (x - 1)B. 1 / (x + 1)C. 1 / (x^2 - 1)D. 1 / (x - 2)8. 下列各式中，平行四边形面积最大的是（）A. 底边长为5，高为4B. 底边长为4，高为5C. 底边长为6，高为3D. 底边长为3，高为69. 下列各式中，勾股数是（）A. 3, 4, 5B. 5, 12, 13C. 6, 8, 10D. 7, 24, 2510. 下列各式中，不等式正确的是（）A. 2x + 3 > 5B. 3x - 2 < 7C. 4x + 1 ≥ 6D. 5x - 3 ≤ 8二、填空题（每题5分，共20分）11. 2a - 3b = 0，若a = 3，则b = _______。

12. 已知x^2 - 4x + 4 = 0，则x的值为 _______。

13. (a - b)^2 = 9，若a = 3，则b = _______。

数学初二上测试题及答案一、选择题（每题3分，共30分）1. 下列哪个数是无理数？A. 3.14159B. √2C. 0.1010010001…D. 2/32. 如果一个数的相反数是它本身，那么这个数是：A. 0B. 1C. -1D. 23. 一个数的绝对值是它自身的数是：A. 正数B. 负数C. 零D. 正数和零4. 下列哪个选项是方程 x^2 - 4 = 0 的解？A. x = 2B. x = -2C. x = 2 或 x = -2D. x = 05. 一个数的立方根是它自己，那么这个数是：A. 1B. -1C. 0D. 1, -1, 06. 一个数的平方是它自己，那么这个数是：A. 1B. -1C. 0D. 1, 07. 一个数的倒数是它自己，那么这个数是：A. 1B. -1C. 0D. 1, -18. 一个数的平方根是它自己，那么这个数是：A. 1B. -1C. 0D. 1, 09. 一个数的立方是它自己，那么这个数是：A. 1B. -1C. 0D. 1, -1, 010. 一个数的平方是16，那么这个数是：A. 4B. -4C. 4 或 -4D. 0二、填空题（每题3分，共30分）1. 一个数的绝对值是4，那么这个数可以是_________。

2. 一个数的相反数是-5，那么这个数是_________。

3. 一个数的平方是25，那么这个数是_________。

4. 一个数的立方是-8，那么这个数是_________。

5. 一个数的倒数是1/2，那么这个数是_________。

6. 一个数的平方根是3，那么这个数是_________。

7. 一个数的立方根是2，那么这个数是_________。

8. 一个数的平方是9，那么这个数是_________。

9. 一个数的立方是27，那么这个数是_________。

10. 一个数的平方根是-2，那么这个数是_________。

三、解答题（每题10分，共40分）1. 计算：(2x + 3)(x - 4)。

初二数学入学测试题时间:60分钟 满分:100分学校： 姓名： 分数：1.在平面直角坐标系中，点P (－2， 1)所在的象限是（ ） A.第一象限 B .第二象限 C.第三象限 D.第四象限2.16的算术平方根是 （ ）A 、±4B 、4C 、±2D 、2 3、下列图中∠１与∠２是对顶角的是（ ）4、下列语句正确的是（ ） A ．64的立方根是2 B ． －3是27的立方根 C ．216125的立方根是65D ． （－1）2的立方根是－15、将点Ａ（－２，－３）向左平移３个单位长度得到点Ｂ，则点Ｂ的坐标是（ ） Ａ、（１，－３） Ｂ、（－２，０） Ｃ、（－５，－３） Ｄ、（－２，－６）6、已知：如图，由ＡＤ∥ＢＣ，可以得到 （ ） Ａ ∠１＝∠２ Ｂ ∠３＝∠４ Ｃ ∠２＝∠３ Ｄ ∠１＝∠４7、点Ｃ在x 轴的下方，y 轴的右侧，距离x 轴３个单位长度，距离y 轴５个单位长度，则点Ｃ的坐标为（ ） Ａ、（－３，５） Ｂ、（３，－５） Ｃ、（５，－３） Ｄ、（－５，３） 8、在实数：3.14159，364，1.010010001…，，π，722中，无理数有（ ） D21C21B 21A 21第（8）题D C BA第5题12 3 4A ．1个B ．2个C ．3个D ．4个9.如图，有一块含有45°角的直角三角板的两个顶点放在直尺的对边上.如果∠1＝20°，那么∠2的度数是（ ）A.30°B.25°C.20°D.15°10.如图，直线AB 、CD 相交于点O ，OT ⊥AB 于O ，CE ∥AB 交CD 于点C ，若∠ECO =30°，则∠DOT 等于（ ）A.30°B.45°C. 60°D. 120°11.下列调查中，适合用普查方式的是（ ）A. 了解一批炮弹的杀伤半径B. 了解启东电视台《小城阳光》栏目的收视率C. 了解长江中鱼的种类D. 了解某班学生对“启东精神”的知晓率12．为了解某市七年级一次期末数学测试情况，从8万名考生中抽取了1000名学生的数学成绩进行统计分析，下列说法中正确的是（ ）.A ．这1000名学生是总体的一个样本B ．每位学生的数学成绩是个体C ．8万名学生是总体D ．1000名学生是样本容量 13. 下列说法中，错误．．的是（ ） A. 不等式2<x 的正整数解只有一个 B. 2-是不等式012<-x 的一个解 C. 不等式93>-x 的解集是3->x D. 不等式10<x 的整数解有无数个 14．不等式组的解集在数轴上表示为（ ）B15．有40个数据，共分成6组，第1～4组的频数分别为10，5，7，6，第5组的频率是0.1，则第6组的频数是（ ）.第10题图第9题图A 、8B 、28C 、32D 、4016．某市股票在七个月之内增长率的变化状况如图3所示．从图上看出，下列结论不正确的是（ ）． Ａ．2~6月份股票月增长率逐渐减少 Ｂ．7月份股票的月增长率开始回升 Ｃ．这七个月中，每月的股票不断上涨 Ｄ．这七个月中，股票有涨有跌17．某种出租车的收费标准：起步价7元（即行驶距离不超过3千米都需付7元车费），超过3千米后，每增加1千米，加收2.4元（不足1千米按1千米计）．某人乘这种出租车从甲地到乙地共付车费19元，那么甲地到乙地路程的最大值是（ ） Ａ．5千米 Ｂ．7千米 Ｃ．8千米 Ｄ．15千米18.如果不等式组⎩⎨⎧<>2x a x ，恰有3个整数解，则a 的取值范围是（ ） A.1-≤a B.1-<a C.12-<≤-a D.12-≤<-a19、一船顺水航行45千米需要3小时，逆水航行65千米需要5小时，若设船在静水中的速度为x 千米/时，水流速度为y 千米/时，则x 、y 的值为 （ ）A ⎩⎨⎧==213y xB ⎩⎨⎧==114y xC ⎩⎨⎧==115y xD ⎩⎨⎧==214y x20、不等式45111x -<的正整数解为（ ） A 、1个 B 、3个 C 、4个 D 、5个21、买苹果和梨共50千克，其中苹果的重量是梨的2倍少8千克，求苹果和梨各买多少？若设买苹果x 千克，买梨y 千克，则列出的方程组应是 （ ）A 、⎩⎨⎧+==+8250x y y xB 、⎩⎨⎧-==+8250x y y xC 、⎩⎨⎧+==+8250y x y xD 、⎩⎨⎧-==+8210y x y x22．用代入法解方程组⎩⎨⎧=-=+243y x y x 使得代入后化简比较容易的变形是（ ）A . 由①，得342y x -=B . 由①，得432xy -=C . 由②, 得25+=y x D . 由②, 得52-=x y23、若方程组⎩⎨⎧-=++=+ay x ay x 13313的解满足y x +＞0，则a 的取值范围是（ ）A 、a ＜－1B 、a ＜1C 、a ＞－1D 、a ＞124、六一儿童节到了要把一些苹果分给几个小朋友，如果每人分3个，则剩8个；如果每人分5个，那么最后一个小朋友就分不到3个，则共有多少个小朋友( )A.4B.5C.6D.725．如图，一把矩形直尺沿直线断开并错位，点E 、D 、B 、F 在同一条直线上，若∠ADE=125°，则∠DBC 的度数为（ ）26．若a <b ，则5-5b；12-a 12-b ． 27．点 P （a+1，a ﹣3）在第三象限，则a 的取值范围是 ．28．为配合“禁烟”行动，某校组织开展了“吸烟有害健康”的知识竞赛，共有20道题.答对一题记10分，答错（或不答）一题记－5分.小明参加本次竞赛得分要超过100分，他至少要答对 道题.29. 某商品进价是1000元，售价为1500元．为促销，商店决定降价出售，但保证利润率不低于5％，则商店最多降元出售商品．30、如图④，AB∥CD，∠BAE = 120º，∠DCE = 30º，则∠AEC = 度。

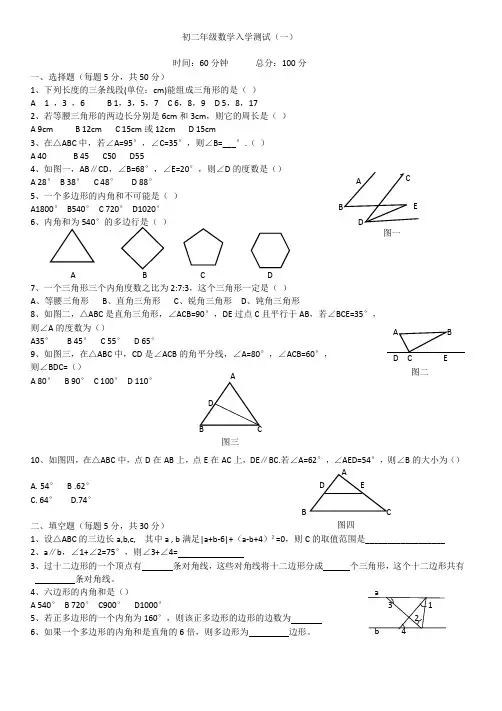
初二年级数学入学测试（一）时间：60分钟 总分：100分一、选择题（每题5分，共50分）1、下列长度的三条线段(单位：cm)能组成三角形的是（ ）A 1 ，3 ，6B 1，3，5，7C 6，8，9D 5，8，172、若等腰三角形的两边长分别是6cm 和3cm ，则它的周长是（ ）A 9cmB 12cmC 15cm 或12cmD 15cm3、在△ABC 中，若∠A=95°，∠C=35°，则∠B=___°.（ ）A 40B 45 C50 D554、如图一，AB ∥CD ，∠B=68°，∠E=20°，则∠D 的度数是（） A 28° B 38° C 48° D 88°5、一个多边形的内角和不可能是（ ）A1800° B540° C 720° D1020°6AC D7、一个三角形三个内角度数之比为2:7:3，这个三角形一定是（ ）A 、等腰三角形B 、直角三角形C 、锐角三角形D 、钝角三角形8、如图二，△ABC 是直角三角形，∠ACB=90°，DE 过点C 且平行于AB ，若∠BCE=35°，则∠A 的度数为（） A35° B 45° C 55° D 65° 9、如图三，在△ABC 中，CD 是∠ACB 的角平分线，∠A=80°，∠ACB=60°， 则∠BDC=（） A 80° B 90° C 100° D 110°10、如图四，在△ABC 中，点D 在AB 上，点E 在AC 上，DE ∥BC.若∠A=62°，∠AED=54°，则∠B 的大小为（）A. 54° B .62°C. 64°D.74°二、填空题（每题5分，共30分）1、设△ABC 的三边长a,b,c, 其中a , b 满足|a+b -6|+（a -b+4）²=0，则C 的取值范围是__________________2、a ∥b ，∠1+∠2=75°，则∠3+∠4=3、过十二边形的一个顶点有 条对角线，这些对角线将十二边形分成 个三角形，这个十二边形共有 条对角线。

一、选择题（每题3分，共30分）1. 下列各数中，是整数的是（）A. -3.14B. 0.001C. √2D. 52. 若a、b是实数，且a < b，则下列不等式中正确的是（）A. a + 1 < b + 1B. a - 1 < b - 1C. a + 2 < b + 2D. a - 2 < b - 23. 下列图形中，具有对称性的是（）A. 长方形B. 等腰三角形C. 矩形D. 正方形4. 若x^2 - 5x + 6 = 0，则x的值为（）A. 2B. 3C. 2或3D. 无法确定5. 在直角坐标系中，点P（-2，3）关于x轴的对称点为（）A. （-2，-3）B. （2，-3）C. （-2，3）D. （2，3）6. 若一个等边三角形的边长为a，则其周长为（）A. 3aB. 2aC. aD. a/27. 下列函数中，y是x的一次函数的是（）A. y = x^2 + 2B. y = 3x - 5C. y = 2x + 3D. y = 5x^2 + 28. 下列各数中，是正数的是（）A. -2B. 0C. -1/3D. 1/29. 若a、b、c是三角形的三边，且a + b > c，则下列结论正确的是（）A. a > c - bB. b > c - aC. c > a - bD. a > b - c10. 下列各式中，正确的是（）A. (a + b)^2 = a^2 + b^2B. (a - b)^2 = a^2 - b^2C. (a + b)^2 = a^2 + 2ab + b^2D. (a - b)^2 = a^2 - 2ab + b^2二、填空题（每题5分，共20分）11. 若x = 3，则x^2 - 2x + 1的值为______。

12. 若a、b、c是等差数列的前三项，且a + b + c = 12，则a = ______。

13. 在直角坐标系中，点A（2，3）关于原点的对称点为______。

黑龙江省哈尔滨市德强中学2024-2025学年八年级上学期开学测试数学试题一、单选题1．下列方程中，是二元一次方程的是（ ）A ．25x y +=B ． 3xy =C ．235x y +=D ．11y x+= 2．用不等式表示图中的解集，正确的是 （ ）A ．4x >B ．2x ≥C ．2x <D ．2x ≤ 3．若12x y =⎧⎨=-⎩是方程35x ay +=的解，则a 的值是（ ） A ．4 B ．－1 C ．1 D ．－44．如果0m n <<，那么下列结论中错误的是（ ）A ．11m n -<-B ．m n ->-C ．0m n ->D ．1m n> 5．嘉兴某校项目化学习小组研究“三角形周长”的课题，将3根木棒首尾相连围成一个三角形，其中两根木棒的长分别为10cm 、3cm ，则该三角形的周长可能是（ ） A ．18cm B ．19cm C ．20cm D ．21cm 6．一个多边形每一个外角都等于45︒，则这个多边形的边数为（ ）A ．12B ．10C ．8D ．67．甲，乙二人赛跑，如果乙比甲先跑8m ，那么甲跑4s 就能追上乙；如果甲让乙先跑1s ，那么甲跑3s 就能追上乙，设甲，乙每秒分别跑m x 和m y ，则可列出的方程组是（ ）A ．44833x y x y y =+⎧⎨=+⎩B ．484331x y x y +=⎧⎨-=⎩C ．448313x y x y =+⎧⎨-=⎩D ．448313x y x y =+⎧⎨-=⎩8．如图，小明书上的三角形被墨迹污染了一部分，他根据所学的知识很快就画了一个与书上完全一样的三角形，那么小明画图的依据是（ ）A ．SSSB ．SASC ．AASD ．ASA9．如图，ABC V 中，B C ∠=∠，BD CF =，BE CD =，EDF α∠=，则下列结论正确的是（ ）A ．2180A α+∠=︒B ．90A α+∠=︒C ．290A α+∠=︒D ．180A α+∠=︒ 10．如图，在ABC V 中，D 是AB 上一点，DF 交AC 于点E ，AE EC =，=DE EF ，则下列结论中：①ADE EFC ∠=∠；②180ADE ECF FEC ∠+∠+∠=︒；③+180B BCF ∠∠=︒；④ABC DBCF S S =V 四边形，正确的结论有( )A ．4个B ．3个C ．2个D ．1个二、填空题11．已知48x y +=，用含x 的代数式表示y ，则y =12．“y 的3倍与5的和不小于3-”用不等式表示为．13．已知不等式()11a x a ->-的解集是1x <，则a 的取值范围为．14．已知一组数据：8， 4， 5， 4， a ， 7的平均数为5， 则这组数据的中位数是． 15．如图，在△ABC 中，∠ACB ＝90°，将△ACD 沿CD 折叠，使点A 恰好落在BC 边上的点E 处．若∠B ＝26°，则∠BDE ＝．16．如图，1AP 为ABC V 的中线，2AP 为1APC V 的中线， 3AP 为2V APC 的中线，…，按此规律，n AP 为1-V n AP C 的中线．若ABC V 的面积为64，则5APC V 的面积为．17．在ABC V 中，AD ，BE 为三角形的高，M 为AD ，BE 所在直线的交点52BMD ∠=︒，则C ∠的度数是．18．如图，在ABD △中，BF 是中线，DE BF ⊥于点E ，AC BF ⊥交BF 延长线于点C ，DE EC =，EP AD ∥交AB 于点P ，且PEC BDE ∠=∠，若BDF V 的面积为5，则FC 长为．三、解答题19．解方程组：(1)3211354x y x y +=⎧⎨-=⎩(2)2411232x y x y +=⎧⎪++⎨+=⎪⎩ 20．不等式或不等式组：(1)()2421x x -<-；(2)()523131722x x x x ⎧+>-⎪⎨-≤-⎪⎩ 21．如图，在88⨯的网格中，每一小格均为正方形且边长是1，已知ABC V ．(1)画出ABC V 中AB 边上的高CE ；(2)用一条线段将ABC V 分成面积相等的两部分（线段的端点是小正方形的顶点）；(3)画一个格点三角形，使之与ABC V 全等．22．为了让同学们了解自己的体育水平，初二1班的体育老师对全班45名学生进行了一次体育模拟测试(得分均为整数)，成绩满分为10分，1班的体育委员根据这次测试成绩，制作了统计图和分析表如下：根据以上信息，解答下列问题：(1)这个班共有男生______________人，共有女生______________人；(2)求初二1班女生体育成绩的众数是______________分，男生体育成绩的平均数是______________分．(3)若全年级有540名学生，体育测试9分及以上成绩为优秀，试估计全年级体育测试成绩优秀的有多少名学生?23．阅读以下例题：解不等式：()()410x x +->．解：①当40x +>，则10x ->，即可以写成：4010x x +>⎧⎨->⎩，解不等式组得：1x >． ②当若40x +<，则10x -<，即可以写成：4010x x +<⎧⎨-<⎩，解不等式组得：<4x -． 综合以上两种情况：原不等式的解集为：1x >或<4x -．以上解法的依据为：当0ab >，则ab 同号．请你模仿例题的解法，解不等式：(1)()()120x x +->；(2)()()21320x x -+<．24．某商店欲购进A ，B 两种商品，已知购进A 种商品3件和B 种商品2件，共需170元；若购进A 种商品4件和B 种商品6件，共需310元．(1)求A ，B 两种商品每件的进价分别是多少元?(2)若该商店每件A 种商品售价是45元，每件B 种商品售价为28元，且商店将购进A ，B 共50件的商品全部售出后，要获得的利润不低于210元，问A 种商品至少购进多少件?25．如图，在平面直角坐标中，点O 为坐标原点，AOB V 中，(0,)(0)A m B n ，，，其中()2390m n --=；(1)如图1，求出点A 和点B 的坐标；(2)如图2，点P 从点B 出发，以每秒2个单位长度的速度沿x 轴负方向运动，设点P 的运动时间为t 秒．连接AP ，设AOP V 的面积为S ，用含有t 的式子表示S ；(3)如图3，在（2）的条件下，点P 在线段OB 上时，过点B 作BC OB ⊥于点B ，连接AC PC 、，且AB AC CAB CPB =∠=∠，；当12S =时．求APC △的面积26．如图1，Rt ABC △中，90ACB ∠=︒，点D 在BC 延长线上，DE BC ⊥，DE BC =，连接BE 交AC 与点F ，且902ABF BAC ∠=︒-∠．(1)如图1，求证：AB BE =；(2)如图2，过点E 作EH AC ⊥于点H ，EH AH =，连接BH ，求证：BH 平分ABE ∠；(3)如图3，在（2）的条件下，过点B 作AB 的垂线交AC 的延长线于点G ，2BE BG =，27AEF S =V ，求AG 的长．。

一、选择题（每题4分，共40分）1. 下列各数中，有理数是（）A. √9B. √-16C. √0D. √32. 若a=3，b=-2，则a²+b²的值为（）A. 7B. 9C. 5D. 13. 下列代数式中，同类项是（）A. 2x²B. 3x²yC. 4xyD. 5x²4. 已知等腰三角形ABC中，AB=AC，若∠B=50°，则∠A的度数是（）A. 40°B. 50°C. 60°D. 70°5. 下列图形中，是轴对称图形的是（）A. 正方形B. 等边三角形C. 等腰梯形D. 长方形6. 若a、b、c、d是等差数列的前四项，且a+b+c+d=20，则b²的值为（）A. 5B. 10C. 15D. 207. 下列函数中，有最大值的是（）A. y=2x+1B. y=x²-3x+2C. y=-x²+4x-3D. y=x³-2x²+3x-18. 下列方程中，无解的是（）A. 2x+3=7B. 3x-4=1C. 5x+2=0D. 4x-5=09. 下列各数中，绝对值最小的是（）A. -3B. 0C. 3D. -510. 若a、b、c是等比数列的前三项，且a+b+c=24，b=4，则c的值为（）A. 3B. 6C. 8D. 12二、填空题（每题4分，共40分）11. 0.125的分数形式是__________。

12. 若x²-5x+6=0，则x的值为__________。

13. 在△ABC中，若AB=AC，则∠A=__________。

14. 若x²+4x+4=0，则x的值为__________。

15. 若等差数列的前三项分别为1，3，5，则该数列的公差为__________。

16. 若等比数列的前三项分别为2，6，18，则该数列的公比为__________。

初二数学入学测试题（含答案）姓 名 学校 成绩一、选择题（每道题7分，共42分）1．有理数a 、b 在数轴上的位置如图所示，那么下列式子中成立的是（ ）A ．a<bB ．a>bC ．ab>0D ．ba >0 2．下列说法错误的是（ ）A ．1是2(-1)的算术平方根B ．7)7(2=-C ．27-的立方根是3-D ．12144±=3．等腰三角形两边长分别为4，8，则它的周长为( )A ．20B ．16C ．20或16D ．不能确定4．二元一次方程2534=+y x 的正整数解有( )A ．1个B ．2个C ．3个D ．4个5．如果p （a －3，a+1）在第二象限，那么a 的取值范围是A ．a>－1B ．a<3C ．－3<a<3D ．一1<a<36．计算机的存储单位有：字节B ，千字节KB ，兆字节MB ，1MB ＝1024 KB ，1KB ＝1024B ，两个 字节相当于一个汉字，那么一张容量为1.44MB 的软盘最多可存储多少个汉字?用科学记数法表示为（保留三个有效数字）（ ）A ．7.55×104B ．7.55×106C ．7.55×105D ．7.54×104二、填空题（每题7分，共28分）7、不等式组⎩⎨⎧->+>--1214)2(3x x x x 的解集是_______． 8、已知△ABC 的高为AD ，∠BAD=70°，∠CAD=20°，则∠BAC 的度数是_______9．如果01622=-a ，那么a 的算术平方根是_________．10、观察下面一列数：根据规律写出横线上的数，－11；21；－31；___；－51；61；______;…．，第2007个数是__________。

三、化简求值（本题10分）11、化简求值y x xy y x xy xy xy 2222332323+⎥⎦⎤⎢⎣⎡+⎪⎭⎫ ⎝⎛---其中31,3-==y x四、解答题（本小题满20分）12．为了防控甲型H1N1流感，某校积极进行校园环境消毒，购买了甲乙两种消毒液共100瓶，其中甲种消毒液6元／瓶，乙种消毒液9元／瓶。

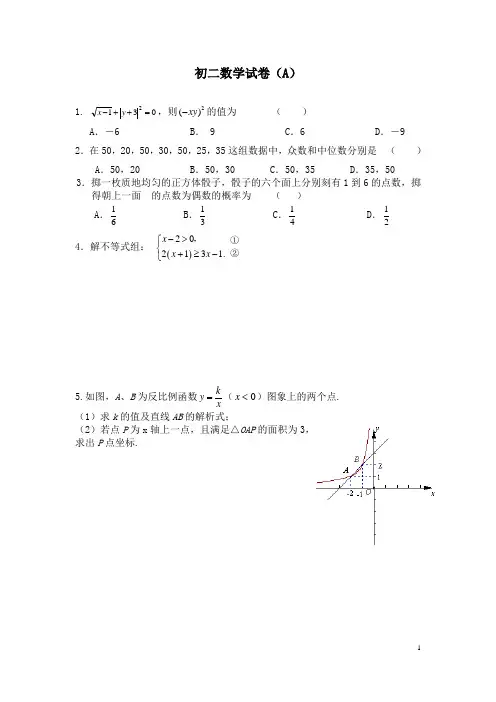
初二数学试卷（A ）1. 0312=++-y x ，则2()xy -的值为 （ ） A ．－6B ． 9C ．6D ．－92．在50，20，50，30，50，25，35这组数据中，众数和中位数分别是 （ ） A ．50，20 B ．50，30 C ．50，35 D ．35，503．掷一枚质地均匀的正方体骰子，骰子的六个面上分别刻有1到6的点数，掷得朝上一面 的点数为偶数的概率为 （ ）A ．61 B ．31 C ．41 D ．214．解不等式组： ()20213 1.x x x ->⎧⎨+≥-⎩，5.如图，A 、B 为反比例函数xky =（0<x ）图象上的两个点. （1）求k 的值及直线AB 的解析式；（2）若点P 为x 轴上一点，且满足△OAP 的面积为3， 求出P 点坐标.①②6．列方程或方程组解应用题：在城区改造项目中，区政府对某旧小区进行节能窗户改造．该小区拥有相同数量的A、B两种户型．已知所有A户型窗户改造的总费用为54万元，所有B户型窗户改造的总费用为48万元，且B户型窗户的每户改造费用比A户型窗户的每户改造费用便宜500元．问A、B两种户型的每户窗户改造费用各为多少元？7．问题背景（1）如图1，△ABC中，DE∥BC分别交AB，AC于D，E两点，过点D作DF∥AC交BC于点F．请按图示数据填空：四边形DFCE的面积S=，△DBF的面积S=，1△ADE的面积S=．2探究发现（2）在（1）中，若BF a=，DＧ=，FC b与BC间的距离为h．直接写出S=（用2S的代数式表示）．含S、1拓展迁移（3）如图2，□DEFG的四个顶点在△ABC的三边上，若△ADG、△DBE、△GFC的面积分别为4、8、1，试利用．．．．求□DEFG的．．（2．）中的结论面积，直接写出结果．8．已知关于x的方程0+kxxk．+-k+23)1(2=（1）若方程有两个不相等的实数根，求k的取值范围；（2）当方程有两个相等的实数根时，求关于y的方程2(4)10y a k y a+-++=的整数根（a为正整数）．9．已知：正方形ABCD 中，45MAN ∠=o ，绕点A 顺时针旋转，它的两边分别交CB 、DC （或它们的延长线）于点M 、N ．（1）如图1，当MAN ∠绕点A 旋转到BM DN =时，有BM DN MN +=．当MAN ∠ 绕点A 旋转到BM DN ≠时，如图2，请问图1中的结论还是否成立？如果成立，请给予证明，如果不成立，请说明理由；（2）当MAN ∠绕点A 旋转到如图3的位置时，线段BM DN ，和MN 之间有怎样的等量关系？请写出你的猜想，并证明．10.已知：在△ABC 中，BC =2AC ，∠DBC =∠ACB ，BD =BC ，CD 交线段AB 于点E ． （1）如图l ，当∠ACB =90°时，直接写出线段DE 、CE 之间的数量关系； （2）如图2，当∠ACB =120°时，求证：DE =3CE ；（3）如图3，在（2）的条件下，点F 是BC 边的中点，连接DF ，DF 与AB 交于G ，△DKG 和△DBG 关于直线DG 对称（点B 的对称点是点K ），延长DK 交AB 于点H ．若BH =10，求CE 的长.图 1ED ACB 图 2EDACBF GKH图 3EDACB答案1、 B （5分）2、 C （5分）3、 D （5分）4、 由不等式①解得 2x >, …………………………3分由不等式②解得 3x ≤. …………………………6分 因此不等式组的解集为23x <≤. …………………………9分 5、解：（1）由题意得，21-=k∴k= -2. ……………………………3分 设AB 的解析式为y=ax+b. 由题意得，⎩⎨⎧=+-=+-212b a b a解得，⎩⎨⎧==31b aAB 的解析式为y= x+3 ……………………….6分（2）设点P （x ，0）由题意得，S △OAP =121⋅⋅OP =3 OP=6………………………………9分点P 坐标为（-6,0）或（6,0）………………………….13分6．解：设A 户型的每户窗户改造费用为x 元，则B 户型的每户窗户改造费用为(500)x -元． ……………………………… 2分 根据题意，列方程得5400004800005x x =-． 解得 4500x =．经检验，4500x =是原方程的解，且符合题意．…………………………… 6分 ∴5004000x -=．答：A 户型的每户窗户改造费用为4500元，B 户型的每户窗户改造费用为4000 元．…………………………………… 8分7、解：（1）四边形DFCE 的面积S = 6 ，△DBF 的面积1S = 6 ，△ADE 的面积2S = 32 ． …………………………………… 9分（2）2S = 214S S （用含S 、1S 的代数式表示）． ………… 12分（3）□DEFG 的面积为12． ………………………………………… 15分8、解：（1）△=244(1)(3)k k k --+=2244812k k k --+=812k -+ ……………………………………………………………… 3分∵方程有两个不相等的实数根，∴10,0.k -≠⎧⎨∆>⎩ 即 10,8120.k k -≠⎧⎨-+>⎩∴k 的取值范围是32k <且1k ≠． ……………………………………8分 （2）当方程有两个相等的实数根时，△=812k -+=0．∴32k =． ………………………………………………………………… 13分 ∴关于y 的方程为2(6)10y a y a +-++=．∴2'(6)4(1)a a ∆=--+2123644a a a =-+--21632a a =-+2(8)32a =--．由a 为正整数，当2(8)32a --是完全平方数时，方程才有可能有整数根． 设22(8)32a m --=（其中m 为整数），32p q =g （p 、q 均为整数）， ∴22(8)32a m --=．即(8)(8)32a m a m -+--=． 不妨设8,8.a m p a m q -+=⎧⎨--=⎩两式相加，得 162p q a ++=．∵(8)a m -+与(8)a m --的奇偶性相同，∴32可分解为216⨯，48⨯，(2)(16)-⨯-，(4)(8)-⨯-， ∴18p q +=或12或18-或12-．∴17a =或14或1-（不合题意，舍去）或2．当17a =时，方程的两根为1172y -±=，即12y =-，29y =-．…15分 当14a =时，方程的两根为822y -±=，即13y =-，25y =-．…… 17分当2a =时， 方程的两根为422y ±=，即13y =，21y =． ………… 20分9、解：（1）答：（1）中的结论仍然成立，即 BM DN MN +=．证明：如图2，在MB 的延长线上截取BE =DN ，连结AE ．易证 ABE ADN △≌△ （SAS ）． ∴ AE =AN ；∠EAB=∠NAD．90,45,45.45.BAD NAM BAM NAD EAB BAM ∠=∠=∴∠+∠=∴∠+∠=o o ooQ∴EAM NAM ∠=∠．又AM 为公共边， ∴AEM ANM △≌△． ME MN ∴=．MN ME BE BM DN BM ∴==+=+即 DN BM MN +=． ------------------------------------10分 （2）猜想：线段BM DN ，和MN 之间的等量关系为：DN BM MN -= ．证明：如图3，在DN 延长线上截取DE =MB ，连结A E ．易证 ABM ADE △≌△（SAS ）． ∴ AM =AE ；∠MAB =∠EAD ． 易证 AMN AEN △≌△（SAS ）．MN EN ∴= ．∵DN DE EN -=，∴DN BM MN -=． ----------------------------10分 10.(1)DE=2CE………………………2分 (2)证明：过点B 作BM ⊥DC 于M ∵BD=BC ，∴DM=CM, ………………………..5分∴∠DMB=∠CMB=90°,∠DBM=∠CBM=21∠DBC=60° ∴∠MCB=30° BM=21BC ∵BC=2AC ，∴BM=AC. ∵∠ACB=120°, ∴∠ACE=90°. ∴∠BME=∠ACE ∵∠MEB=∠AEC ∴△EMB ≌△ECA ∴ME=CE=21CM ………………………10分 ∴DE=3EC ………………………………12分(3) 过点B 作BM ⊥DC 于M ，过点F 作FN ⊥DB 交DB 的延长线于点N.图 2MEDACB∵∠DBF=120°, ∴∠FBN=60°. ∴FN=23BF,BN=21BF ……5分 ∵DB=BC=2BF, DN=DB+BN=25BF ∴DF=7BF ∵AC=21BC,BF=21BC ∴AC=BF∵∠DBC=∠ACB ∴△DBF ≌BCA ∴∠BDF=∠CBA. ∵∠BFG=∠DFB, ∴△FBG ∽△FDB ∴DBBGDF BF BF FG == ∴FD FG BF ⋅=2,∴77=FG BF ∴DG=776BF,BG=772BF ∵△DKG 和△DBG 关于直线DG 对称，∴∠GDH=∠BDF.∠ABC=∠GDH. ∵∠BGF=∠DGA, ∴△BGF ∽△DGH. ∴GHGFDG BG =. ∴GH=773BF. ∵BH=BG+GH=775BF=10, ∴BF=72. ……………………………15分 ∴BC=2BF=47 ,CM=212 ∴CD=2CM=214. ∵DE=3EC ∴EC=41CD=21 …………………………….20分 NM 图 3HK G F EDACB。