几何体的截面三视图平面展开图
- 格式:doc
- 大小:814.00 KB
- 文档页数:8

立体几何中的截面(解析版)在立体几何中,截面是指用一个平面去截一个几何体(包括圆柱、圆锥、球、棱柱、棱锥、长方体、正方体等),得到的平面图形。
总共有三种截面方式,分别为横截、竖截、斜截。
我们需要了解每一种立体图形通过上述三种截面方式所得到的截面图有哪些。
正六面体的基本斜截面不会出现以下几种图形:直角三角形、钝角三角形、直角梯形、正五边形。
圆柱体的基本截面也有其特殊性质。
我们可以运用线、面平行的判定定理与性质求截面问题,或者结合线、面垂直的判定定理与性质定理求正方体中截面问题。
此外,我们还可以灵活运用一些特殊图形与几何体的特征,“动中找静”,如正三角形、正六边形、正三棱锥等。
建立函数模型也是求最值问题的一种方法。
在一个透明的塑料制成的长方体内灌进一些水,固定底面一边于地面上,再将倾斜,有四个命题。
其中,水的部分始终呈棱柱状,棱AD始终与水面平行,当倾斜到如图5(2)时,BE·BF是定值。
水面的面积在转动过程中会改变,而BC//FG//A1D1,所以A1D1//面EFGH。
因此,正确的命题序号为①③④。
一个容积为1立方单位的正方体,在棱AB、BB1及对角线B1C的中点各有一小孔E、F、G。
若此可以任意放置,则该可装水的最大容积是多少?分析本题,不能用一个平面去截一个正方体,使得截面为五边形。
进一步地,截面也不能为正五边形。
这是因为正方体的每个面都是正方形,而五边形无法与正方形相切。
因此,无论如何调整平面的位置,都不能得到五边形的截面。
而且OE=OC是抛物线的直线准线,所以焦点F在OC上,且OF=OC=1.故选:D二、完形填空在数学课上,老师讲到一个有趣的问题:如何用一个平面去截一个正方体所得截面不能是一个正五边形。
这个问题引起了我的思考,我开始想象一个平面在正方体中穿过的情景。
我发现,如果截面是一个正五边形,那么这个五边形的五条边必须分属于正方体的五个不同的面。
但是,正方体的每两个相对的面是平行的,所以这五条边中必有两条边是平行的。

1.截面可能是圆的几何体,请打“√”正方体、长方体、圆柱、圆锥、球、六棱柱、三棱锥2.截面可能是三角形的几何体,请打“√”正方体、长方体、圆柱、圆锥、球、六棱柱、三棱锥3.截面可能是矩形的几何体,请打“√”正方体、长方体、圆柱、圆锥、球、六棱柱、三棱锥4.截面可能是梯形的几何体,请打“√”正方体、长方体、圆柱、圆锥、球、六棱柱、三棱锥5.截面可能是平行四边形的几何体,请打“√”正方体、长方体、圆柱、圆锥、球、六棱柱、三棱锥6.用一个平面截下面的几何体,截面不可能是三角形的是_______A 圆锥B圆柱C长方体 D 六棱柱7. 正方体的截面不可能是________A 三角形B 四边形C 五边形D 六边形E 七边形8. 基本几何体的三视图(主视图反映物体的长和高,俯视图是长和宽,左视图是高和宽)几何体主视图左视图俯视图圆柱圆锥四棱锥空心圆柱9.由一些大小相同的小正方体搭成的几何体的主视图与俯视图如图所示,则搭成这个几何体的小正方体的个数最多为___,最少为____。
___.10. 如图所示是由若干个相同的小立方体搭成的几何体的俯视图和左视图,则小立方体的个数不可能是( )A.6个B.7个C.8个D.9个11. 如图是由若干个大小相同的正方体搭成的几何体 的三视图,则该几何体所用的正方形的个数是________12.由一些完全相同的小正方体搭成的几何体的主视图和左视图 如图所示,则组成这个几何体的小正方体的个数可能是13. 几个棱长为1的正方体组成的几何体的 三视图如图所示,则这个几何体的体积是____14.几个立方块所搭几何体的俯视图如图所示,小正方形的数字表示在该位置小立方块的个数.请画出这个几何体的主视图和左视图.15.下图,该几何体是_______. 16. 下图,则这个几何体是______17. 下图,该几何体是_______. 18. 下图,三视图表示的几何体是________19.主视图、俯视图和左视图都是..长方形的几何体是_________(填一个即可) 20. 三视图都相同的几何体可能是_________、____________.(有两种类型)3 2 1 1 2 24 1 3主视图左视图2 2 1 3421.下列四个水平放置的几何体中,三视图如图所示的是( )A.B.C.D22.中央电视台有一个非常受欢迎的娱乐节目:墙来了!选手需按墙上的空洞造型摆出相同姿势,才能穿墙而过,否则会被墙推入水池.类似地,有一个几何体恰好无缝隙地以三个不同形状的“姿势”穿过“墙”上的三个空洞,则该几何体为( )A.B.C.D.23.如图所示,下列水平放置的几何体中,俯视图是矩形的是( )A.B.C.D.24. 下列四个几何体中,主视图是三角形的是( )A.B.C.D.25. 下列几何体中,俯视图相同的是( )A①② B①③C②③ D ②④26.下面四个几何体中,左视图是四边形的几何体共有 ( )A 1 个B 2个C 3个D 4个27.下列四个几何体中,主视图与左视图相同的几何体有( )A.1个B.2个C.3个D.4个28.球和圆柱在水平面上紧靠在一起,组成如图所示的几何体,托尼画出了它的三视图,其中他画的俯视图应该是( )A.两个相交的圆B.两个内切的圆C.两个外切的圆D.两个外离的圆29.我国古代数学家利用“牟合方盖”(如图甲)找到了球体体积的计算方法.“牟合方盖”是由两个圆柱分别从纵横两个方向嵌入一个正方体时两圆柱公共部分形成的几何体,图乙所示的几何体是可以形成“牟合方盖”的一种模型,它的主视图是( )。


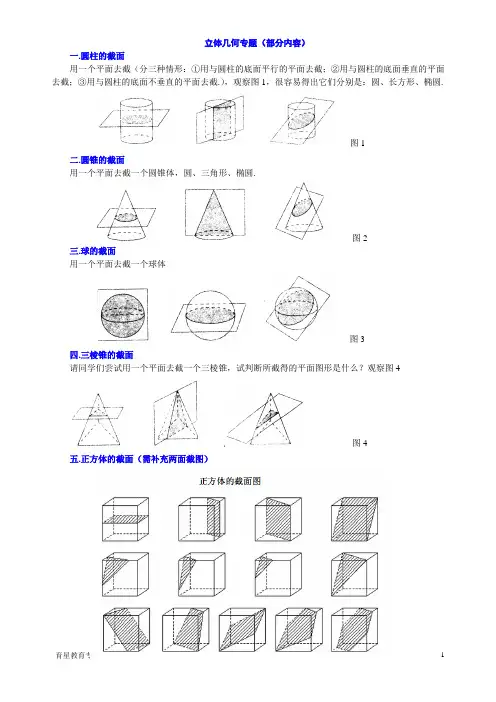
立体几何专题(部分内容)一.圆柱的截面用一个平面去截(分三种情形:①用与圆柱的底面平行的平面去截;②用与圆柱的底面垂直的平面去截;③用与圆柱的底面不垂直的平面去截.),观察图1,很容易得出它们分别是:圆、长方形、椭圆.图1二.圆锥的截面用一个平面去截一个圆锥体,圆、三角形、椭圆.图2三.球的截面用一个平面去截一个球体图3四.三棱锥的截面请同学们尝试用一个平面去截一个三棱锥,试判断所截得的平面图形是什么?观察图4图4五.正方体的截面(需补充两面截图)补充:三视图或投影经典考题公式:空间几何体的表面积棱柱、棱锥的表面积:各个面面积之和圆柱的表面积 :222S rl r ππ=+ 圆锥的表面积:2Srl r ππ=+圆台的表面积:22S rl r Rl R ππππ=+++球的表面积:24SR π=扇形的面积公式2211=36022n R S lr r πα==扇形(其中l 表示弧长,r 表示半径,α表示弧度) 空间几何体的体积 柱体的体积 :VS h =⨯底锥体的体积 :13V S h =⨯底 台体的体积 : 1)3V S S S S h =++⨯下下上上( 球体的体积:343V R π=空间几何体的三视图和直观图:正俯长相等、正侧高相同、俯侧宽一样正视图:光线从几何体的前面向后面正投影,得到的投影图。
侧视图:光线从几何体的左边向右边正投影,得到的投影图。
俯视图:光线从几何体的上面向右边正投影,得到的投影图。
1、线线平行的判断:(1)、平行于同一直线的两直线平行。
(3)、如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线和交线平行。
(6)、如果两个平行平面同时和第三个平面相交,那么它们的交线平行。
(12)、垂直于同一平面的两直线平行。
2、线线垂直的判断:(7)、在平面内的一条直线,如果和这个平面的一条斜线的射影垂直,那么它也和这条斜线垂直。
(8)、在平面内的一条直线,如果和这个平面的一条斜线垂直,那么它和这条斜线的射影垂直。
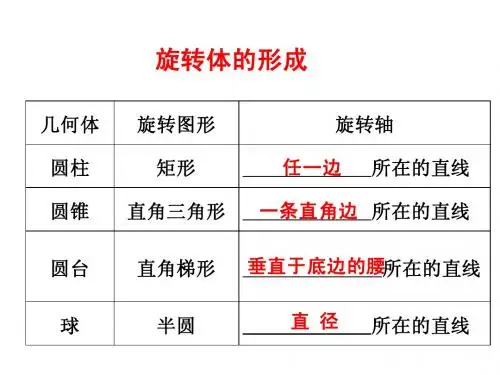





1.截面可能是圆的几何体,请打“√”
正方体、长方体、圆柱、圆锥、球、六棱柱、三棱锥
2.截面可能是三角形的几何体,请打“√”
正方体、长方体、圆柱、圆锥、球、六棱柱、三棱锥
3.截面可能是矩形的几何体,请打“√”
正方体、长方体、圆柱、圆锥、球、六棱柱、三棱锥
4.截面可能是梯形的几何体,请打“√”
正方体、长方体、圆柱、圆锥、球、六棱柱、三棱锥
5.截面可能是平行四边形的几何体,请打“√”
正方体、长方体、圆柱、圆锥、球、六棱柱、三棱锥
6.用一个平面截下面的几何体,截面不可能是三角形的是_______
A 圆锥B圆柱C长方体 D 六棱柱
7. 正方体的截面不可能是________
A 三角形
B 四边形
C 五边形
D 六边形
E 七边形
8. 基本几何体的三视图(主视图反映物体的长和高,俯视图是长和宽,左视图是高和宽)几何体主视图左视图俯视图
圆柱
圆锥
四棱锥
空心圆柱
9.由一些大小相同的小正方体搭成的几何体的主视图与俯视图
如图所示,则搭成这个几何体的小正方体的个数最多为___,最少为____。
___.
10. 如图所示是由若干个相同的小立方体搭成的几何体的
俯视图和左视图,则小立方体的个数不可能是( )
A.6个B.7个C.8个D.9个
11. 如图是由若干个大小相同的正方体搭成的几何体
的三视图,则该几何体所用的正方形的个数是________
12.由一些完全相同的小正方体搭成的几何体的主视图和左视图如图所示,则组成这个几何体的小正方体的个数可能是
13.
几个棱长为
1的正方体组成的几何体的
三视图如图所示,则这个几何体的体积是____
14.几个立方块所搭几何体的俯视图如图所示,小正方形的数字表示在该位置小立方块的个数.请画出这个几何体的主视图和左视图.
15.下图,该几何体是_______. 16. 下图,则这个几何体是______
17. 下图,该几何体是_______. 18. 下图,三视图表示的几何体是________
19.主视图、俯视图和左视图都是
..长方形的几何体是_________(填一个即可)
20. 三视图都相同的几何体可能是_________、____________.(有两种类型)
3
2
1
1
2
2
4
1
3
主视图左视图2
2
1
3
4
21.下列四个水平放置的几何体中,三视图如图所示的是( )
A.B.C.D
22.中央电视台有一个非常受欢迎的娱乐节目:墙来了!选手需按墙上的空洞造型
摆出相同姿势,才能穿墙而过,否则会被墙推入水池.类似地,有一个几何体恰好无缝隙地以三个不同形状的“姿势”穿过“墙”上的三个空洞,则该几何体为( )
A.B.C.D.
23.如图所示,下列水平放置的几何体中,俯视图是矩形的是( )
A.B.C.D.
24. 下列四个几何体中,主视图是三角形的是( )
A.B.C.D.
25. 下列几何体中,俯视图相同的是( )
A①② B①③
C②③ D ②④
26.下面四个几何体中,左视图是四边形的几何体共有 ( )
A 1 个
B 2个
C 3个
D 4个
27.下列四个几何体中,主视图与左视图相同的几何体有( )
A.1个
B.2个
C.3个
D.4个
28.球和圆柱在水平面上紧靠在一起,组成如图所示的几何体,托尼画出了它的三视图,其中他画的俯视图应该是( )
A.两个相交的圆B.两个内切的圆
C.两个外切的圆D.两个外离的圆
29.我国古代数学家利用“牟合方盖”(如图甲)找到了球体体积的计算方法.“牟合方盖”是由两个圆柱分别从纵横两个方向嵌入一个正方体时两圆柱公共部分形成的几何体,图乙所示的几何体是可以形成“牟合方盖”的一种模型,它的主视图是( )。
30.画出下列几何体的主视图:
31.画出下列几何体的俯视图:
32.画出下列几何体的左视图:
33. 如图,是由6个棱长为1个单位的正方体摆放而成的,将正方体A向右平移2个单位,向后平移1个单位后,所得几何体的视图【】
A.主视图改变,俯视图改变B.主视图不变,俯视图不变
C.主视图不变,俯视图改变D.主视图改变,俯视图不变
34. 某几何组合体的主视图和左视图为同一个视图,如图所示,则该几何组合体的
俯视图不可能
...是【】
A. B. C. D.
35. 如图①是一个几何体的主视图和左视图.某班同学在探究它的俯视图时,画出了如图
②的几个图形,其中,可能是该几何体俯视图的共有【】
A.3个B.4个C.5个D.6个
36.如果用□表示1个立方体,用表示两个立方体叠加,用■表示三个立方体叠加,那么下面图是由7个立方体叠成的几何体,从正前方观察,可画出的平面图形是【】
A.B.C.D.
37.李师傅做了一个零件,如图,请你告诉他这个零件的主视图是【】
A.B.C.D.
38.某物体的侧面展开图如图所示,那么它的左视图为()
39.底面半径为3,高为5的圆柱,它的体积是_______.
40. (1)三边长分别为3,4,5的直角三角形..绕长为3的直角边旋转一周得圆锥,请画出圆锥,则母线长为______,求圆锥的体积.
(2)三边长分别为3,4,5的直角三角形..绕长为5的斜边旋转一周(即360°)得到双圆锥,请画出这个几何体,且求这个几何体的体积.
41.如图所示的图形绕虚线旋转一周形成的几何体是( )
42.如图,矩形绕它的一条边MN所在的直线旋转一周形成的几何体是( )
A B.C.D.
43. 将如图所示的Rt△ACB绕直角边AC旋转一周,所得几何体的主视图(正视图)是( )
A.B.C.D.
44.一个长方体的左视图、俯视图及相关
数据如图所示,则其主视图的面积为________
45.如图是一个几何体的三视图,
则这个几何体的侧面积是___________
46.如图是一个上下底密封纸盒的三视图,请根据图中
数据,计算这个密封纸盒的表面积为 _____ cm2.
47. 长方体的主视图、俯视图
如图所示,则其左视图面积为( )
48.一个圆锥的三视图如图所示,
则此圆锥的底面积为______________.
49. 如图所示,水平放置的长方体底面是长为4和宽为2的
矩形,它的主视图的面积为12,则长方体的体积等于_________
50.从棱长为2的正方体毛坯的一角,挖去一个棱长为1的小正方体,
得到一个如图所示的零件,则这个零件的表面积为.
51. 正方体有11种展开图,411,312,222,33,以下各图均有彼此连接的六个小正方形纸片组成,其中不能折叠成一个正方体的是()
A、B、C、D、
52.下列图形中,经过折叠不能围成一个立方体的是()
A. B. C. D.
53. 若下列只有一个图形不是右图的展开图,则此图为()
A B C D
54.表面展开图,则这个几何体是.55. 如图可以折叠成的几何体是_____________
56 圆柱的侧面展开图是__________(填形状名称)
57. 将如图所示表面带有图案的正方体沿某些棱展开后,得到的图形是()
A B C D
58.将图1围成图2的正方体,则图1中的红心“”标志所在的正方形是正方体中的()A.面CDHE B.面BCEF
C.面ABFG D.面ADHG
59. 将“创建文明城市”六个字分别写在一个正方体的六个面上,平面展
开图如图所示,那么在这个正方体中,和“创“相对的字是____
60. 正方体礼品盒,六面上各有一字,连起来就是“预祝中考成功”,其中“预”的对面是“中”,
“成”的对面是“功”,则它的平面展开图可能是( )
61.一个正方体的每一个面都有一个汉字,其平面展开图如图所示,
那么在该正方体中和“城”字相对的字是____
62.如图,立方体的六个面上标着连续的整数,若相对的两个面上 所标之数的和相等,则这六个数的和为 63.将如图所示的正方体的展开图重新折叠
成正方体后,和“应”字相对面上的汉字是 .
64. 右图是正方体的展开图,则原正方体相对两个面上的数字之和的最小值的是 . 65. 如图,将一张边长为3的正方形纸片按虚线裁剪后,恰好围成一个 底面是正三角形的棱柱,这个棱柱的侧面积为_________. 66. 如图,长方体的底面边长分别为2cm 和4cm ,高为5cm .若一只 蚂蚁从P 点开始经过4个侧面爬行一圈到达Q 点,则蚂奴爬行的 最短路径长为_______cm .(请在卷上画部分展开图,用于解题) 67. 如图圆柱的底面周长为6cm ,AC 是底面圆的直径,高BC = 6cm , 点P 是母线BC 上一点且PC =
2
3
BC .一只蚂蚁从A 点出发沿着圆柱体的 表面爬行到点P 的最短距离是________
68. 一个圆锥形的圣诞帽,母线长是30cm,底面半径是10cm ,她想在帽子 上缠一根漂亮的丝带,从A 出发绕帽子侧面一周,至少需要丝带___cm.
69.如图,如果从半径为9cm 的圆形纸片剪去13
圆周的一个扇形,将留
下的扇形围成一个圆锥(接缝处不重叠),那么这个圆锥的高为_____
70. 一圆锥的侧面展开图是半径为2的半圆,则该圆锥的全面积是______
71. 如图,用高为6cm ,底面直径为4cm 的圆柱A 的侧面积展开图,再围成不同于A 的另一个圆柱B , 则圆柱B 的体积为__________
A
A
B C
P
剪创
联城四
东丹。