当前位置：文档之家 › 《由三视图到几何体的展开图》PPT课件

《由三视图到几何体的展开图》PPT课件

  • 格式：ppt
  • 大小：1.73 MB
  • 文档页数：26

下载文档原格式

  / 26

合集下载

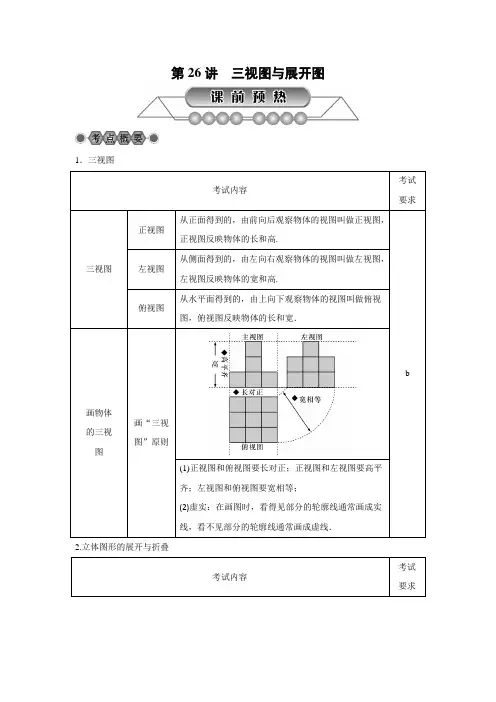
(完整版)第26讲三视图与展开图

(完整版)第26讲三视图与展开图

第26讲三视图与展开图1．三视图考试内容考试要求三视图正视图从正面得到的，由前向后观察物体的视图叫做正视图，正视图反映物体的长和高.b 左视图从侧面得到的，由左向右观察物体的视图叫做左视图，左视图反映物体的宽和高.俯视图从水平面得到的，由上向下观察物体的视图叫做俯视图，俯视图反映物体的长和宽．画物体的三视图画“三视图”原则(1)正视图和俯视图要长对正；正视图和左视图要高平齐；左视图和俯视图要宽相等；(2)虚实：在画图时，看得见部分的轮廓线通常画成实线，看不见部分的轮廓线通常画成虚线．2.立体图形的展开与折叠考试内容考试要求圆锥的侧面展开图圆锥的侧面是一个扇形，能根据展开图想象和制作立体模型．b 直棱柱侧面展开图直棱柱侧面展开图是矩形，能根据展开图想象和制作立体模型．正方体的平面展开图一个立体图形沿不同的棱剪开就得到不同的平面图形．考试内容考试要求基本思想转化思想，将立体图形转化为平面图形，如物体的包装等． b 1．(2017·衢州)如图是由四个相同的小立方体搭成的几何体，它的主视图是()第1题图第2题图2．(2017·丽水)如图是底面为正方形的长方体，下面有关它的三个视图的说法正确的是()A．俯视图与主视图相同B．左视图与主视图相同C．左视图与俯视图相同D．三个视图都相同3．(2017·宁波)如图所示的几何体的俯视图为()4．(2017·金华)一个几何体的三视图如图所示，这个几何体是()A．球B．圆柱C．圆锥D．立方体【问题】如图，下列四个几何体是水平放置．(1)这四个几何体中，主视图与其他三个不相同的是________；(2)图(1)的直三棱柱，底面是边长为2的正三角形，高为4，则此直三棱柱的侧面展开图的面积________；(3)图(2)的圆柱，底面半径为2，高为4，则此圆柱左视图的面积________；(4)通过(1)(2)(3)的解答，请你联想三视图和立体图形展开图的相关知识、方法．【归纳】通过开放式问题，归纳、疏理简单几何体的三视图、展开图．类型一判断(画)几何体的三视图例1下列几何体中，俯视图相同的是()A．①②B．①③C．②③D．②④【解后感悟】掌握从不同方向看物体的方法和画几何体三视图的要求，通过仔细观察、比较、分析，可选出正确答案．1．(1)(2016·湖州)由六个相同的立方体搭成的几何体如图所示，则它的主视图是()(2)(2017·黔西南州)下列四个几何体中，主视图与左视图相同的几何体有()A．1个B．2个C．3个D．4个(3)(2017·台州)如图所示的工件是由两个长方体构成的组合体，则它的主视图是()类型二由三视图判断原几何体的形状例2(2016·黄石)某几何体的主视图和左视图如图所示，则该几何体可能是()A．长方体B．圆锥C．圆柱D．球【解后感悟】由三视图确定几何体，往往需要把三个视图组合起来、空间想象综合考虑；掌握常见几何体的三视图是解题的关键．2．(1)(2015·桂林)下列四个物体的俯视图与如图给出视图一致的是()(2)(2017·嘉兴模拟)如图是某个几何体的三视图，该几何体是()A．长方体B．正方体C．圆柱D．三棱柱(3)(2015·随州)如图是一个长方体的三视图(单位：cm)，根据图中数据计算这个长方体的体积是cm3.类型三立体图形的展开与折叠例3如图给定的是纸盒的外表面，下面能由它折叠而成的是()【解后感悟】常见几何体的展开与折叠：①棱柱的平面展开图是由两个相同的多边形和一些长方形组成，按棱柱表面不同的棱剪开，可能得到不同组合方式的平面展开图，特别关注正方体的表面展开图；②圆柱的平面展开图是由两个相同的圆形和一个长方形组成的；③圆锥的平面展开图是由一个圆形和一个扇形组成的．3．(1)(2017·漳州模拟)如图是一个长方体包装盒，则它的平面展开图是()(2)(2015·广州)如图是一个几何体的三视图，则该几何体的展开图可以是()(3)如图1是边长为1的六个小正方形组成的图形，它可以围成图2的正方体，则图1中小正方形顶点A，B在围成的正方体上的距离是()A．0 B．1 C. 2 D.3(4)(2016·十堰)如图，从一张腰长为60cm，顶角为120°的等腰三角形铁皮OAB中剪出一个最大的扇形OCD，用此剪下的扇形铁皮围成一个圆锥的侧面(不计损耗)，则该圆锥的高为()A．10cm B．15cm C．103cm D．202cm类型四几何体的综合运用例4学校食堂厨房的桌子上整齐地摆放着若干相同规格的碟子，碟子的个数与碟子的高度的关系如下表：碟子的个数碟子的高度(单位：cm)1 22 2＋1.53 2＋34 2＋4.5……(1)当桌子上放有x(个)碟子时，请写出此时碟子的高度(用含x的式子表示)；(2)分别从三个方向上看，其三视图如上图所示，厨房师傅想把它们整齐叠成一摞，求叠成一摞后的高度．【解后感悟】从问题中获取信息(读表)，找出碟子个数与碟子高度之间的关系式是解此题的关键．4．(1)(2017·湖州)如图是按1∶10的比例画出的一个几何体的三视图，则该几何体的侧面积是()A．200cm2B．600cm2C．100πcm2D．200πcm2(2)如图，圆柱形容器高为18cm，底面周长为24cm，在杯内壁离杯底4cm的点B处有一滴蜂蜜，此时一只蚂蚁正好在杯外壁，离杯上沿2cm与蜂蜜相对的点A处，则蚂蚁从外壁A处到达内壁B处的最短距离为cm.【课本改变题】教材母题－－浙教版九下第76页例题如图是某几何体的三视图，则该几何体的体积是()A．18 3 B．54 3 C．108 3 D．216 3 【方法与对策】由三视图求原几何体的体积，正确恢复原几何体是解决问题的关键．这类题是中考热点题型，平时学习中也要注意平面图形和空间图形的转化．【分不清三视图中的实线与虚线】一个空心的圆柱如图所示，那么它的主视图是()参考答案第26讲三视图与展开图【考题体验】1．D 2.B 3.D 4.B【知识引擎】【解析】(1)图(1)的主视图为长方形；图(2)的主视图为长方形；图(3)的主视图为长方形；图(4)的主视图为三角形．故主视图与其他三个不相同的是图(4)．(2)侧面展开图是矩形，侧面积为6×4＝24.(3)左视图的面积为4×4＝16.(4)画三视图，根据三视图描述简单几何体，直棱柱，圆锥侧面展开图等【例题精析】例1②③的俯视图都是圆，有圆心，故选C.例2∵如图所示几何体的主视图和左视图分别是长方形和圆，∴该几何体可能是圆柱体．故选C.例3B例4(1)2＋1.5(x－1)＝(1.5x＋0.5)cm(2)由三视图可知共有12个碟子，∴叠成一摞的高度＝1.5×12＋0.5＝18.5(cm)．【变式拓展】1．(1)A(2)D(3)A 2.(1)C(2)D(3)24 3．(1)A(2)A(3)B(4)D 4.(1)D(2)20 【热点题型】【分析与解】由三视图可看出：该几何体是一个正六棱柱，其中底面正六边形的边长为6，高是2，所以该几何体的体积＝6×34×62×2＝108 3.故选C.【错误警示】A。

展开图-投影与视图PPT精品教学课件

展开图-投影与视图PPT精品教学课件
展开图
学习目标
1、体验立体图形转化为平面图形 的过程； 2、通过观察、想象和动手，发现 立体图形的三视图和展开图； 3、在折叠中发展空间观念； 4、尝试解释猜想结果的合理性。
观察与想象
什么是三视图
1、从正面看(主视图)
2、从侧面看(左视图) 3、从上面看(俯视图)
归纳与总结:
几何体 主视图 左视图 俯视图
3 4 2
2 1
主视图
左视图
1.某两个物体的三视图如图所示.请分别说出它们的形 状.
2.由几个相同的小立方块 搭成的几何体的俯视图如 图所示.方格中的数字表示 该位置的小方块的个数.请 画出这个几何体的三视图.
1
3 2
动手实践
用小立方块搭一个几何体，使得它的主视 图如图所示，这样的几何体只有一种吗？ 它最少有多少个小立方块？最多需要多少 个立方块？摆一摆，试一试。
视图
注意：画三种视图有一定的要求. 主视图反映物体的长和高，俯视 图反映物体的长和宽，左视图反 映物体的高和宽，因此在画三种 视图时，主、俯视图要长对正， 主、左视图要高平齐，左、俯视 图要宽相等.
主 视 图 俯 视 图 左 视 图
视图
⒈图中的几何体你认识吗？
⒉你能想像出它们的主视图、左视图和俯视图吗？ ⒊你能画出它们吗？
探究活动
用6个相同的小方块搭成一 个几何体,它的俯视图如图3-25所 示.则一共有几种不同形状的搭救 法(你可以用实物模型动手试一 试)?你能用三视图表示你探究的 结果吗?
图3-25
• • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • •
左视图
下面图(1)与图(2)是几个小方块所搭几何体俯视图, 小正方形中的数字表示在该位置的小立方块的个数. 请画出这两个几何体的主视图、左视图. 2 4 1 2 3

几何体的截面、三视图、平面展开图

几何体的截面、三视图、平面展开图

1.截面可能是圆的几何体，请打“√”正方体、长方体、圆柱、圆锥、球、六棱柱、三棱锥2.截面可能是三角形的几何体，请打“√”正方体、长方体、圆柱、圆锥、球、六棱柱、三棱锥3.截面可能是矩形的几何体，请打“√”正方体、长方体、圆柱、圆锥、球、六棱柱、三棱锥4.截面可能是梯形的几何体，请打“√”正方体、长方体、圆柱、圆锥、球、六棱柱、三棱锥5.截面可能是平行四边形的几何体，请打“√”正方体、长方体、圆柱、圆锥、球、六棱柱、三棱锥6.用一个平面截下面的几何体，截面不可能是三角形的是_______A 圆锥B圆柱C长方体 D 六棱柱7. 正方体的截面不可能是________A 三角形B 四边形C 五边形D 六边形E 七边形8. 基本几何体的三视图(主视图反映物体的长和高，俯视图是长和宽，左视图是高和宽）几何体主视图左视图俯视图圆柱圆锥四棱锥空心圆柱9.由一些大小相同的小正方体搭成的几何体的主视图与俯视图如图所示，则搭成这个几何体的小正方体的个数最多为___,最少为____。

___．10. 如图所示是由若干个相同的小立方体搭成的几何体的俯视图和左视图，则小立方体的个数不可能是( )A．6个B．7个C．8个D．9个11. 如图是由若干个大小相同的正方体搭成的几何体 的三视图，则该几何体所用的正方形的个数是________12.由一些完全相同的小正方体搭成的几何体的主视图和左视图 如图所示，则组成这个几何体的小正方体的个数可能是13. 几个棱长为1的正方体组成的几何体的 三视图如图所示，则这个几何体的体积是＿＿＿＿14．几个立方块所搭几何体的俯视图如图所示，小正方形的数字表示在该位置小立方块的个数.请画出这个几何体的主视图和左视图.15.下图，该几何体是_______. 16. 下图，则这个几何体是______17. 下图，该几何体是_______. 18. 下图,三视图表示的几何体是________19.主视图、俯视图和左视图都是．．长方形的几何体是_________(填一个即可) 20. 三视图都相同的几何体可能是_________、____________.(有两种类型)3 2 1 1 2 24 1 3主视图左视图2 2 1 3421.下列四个水平放置的几何体中，三视图如图所示的是( )A．B．C．D22.中央电视台有一个非常受欢迎的娱乐节目：墙来了！选手需按墙上的空洞造型摆出相同姿势，才能穿墙而过，否则会被墙推入水池．类似地，有一个几何体恰好无缝隙地以三个不同形状的“姿势”穿过“墙”上的三个空洞，则该几何体为( )A．B．C．D．23.如图所示，下列水平放置的几何体中，俯视图是矩形的是( )A．B．C．D．24. 下列四个几何体中，主视图是三角形的是( )A．B．C．D．25. 下列几何体中，俯视图相同的是( )A①② B①③C②③ D ②④26.下面四个几何体中，左视图是四边形的几何体共有 ( )A 1 个B 2个C 3个D 4个27.下列四个几何体中，主视图与左视图相同的几何体有( )A.1个B.2个C.3个D.4个28.球和圆柱在水平面上紧靠在一起，组成如图所示的几何体，托尼画出了它的三视图，其中他画的俯视图应该是( )A．两个相交的圆B．两个内切的圆C．两个外切的圆D．两个外离的圆29.我国古代数学家利用“牟合方盖”(如图甲)找到了球体体积的计算方法.“牟合方盖”是由两个圆柱分别从纵横两个方向嵌入一个正方体时两圆柱公共部分形成的几何体，图乙所示的几何体是可以形成“牟合方盖”的一种模型，它的主视图是( )。

初中数学精品课件： 三视图与表面展开图

初中数学精品课件： 三视图与表面展开图

A． 国 C． 中
【答案】 B
图 33-4
B． 的 D． 梦
5．(2019·淄博)下列几何体中，其主视图、左视图和俯视图完
全相同的是
()
A．
B
C．
D．
【答案】 D
题型一 判断物体的三视图
三视图是分别从正面、左面、上面三个方向看同一个物体 所得到的平面图形，判断三视图时应注意尺寸的大小，即三个 视图的特征：主视图体现物体的长和高，左视图体现物体的宽 和高，俯视图体现物体的长和宽．
【典例 2】 (2018·青岛)一个由 16 个完全相同的小立方
体搭成的几何体，其最下面一层摆放了 9 个小立方体，
它的主视图和左视图如图 33-7 所示，则这个几何体的
搭法共有
种．
图 33-7
【解析】 这个几何体的搭法共有 10 种，如解图所示．
【答案】 10
(典例 2 解)
【类题演练 2】 如图 33-8 所示的三视图所对应的几何体是 ( )
图 33-9
A． 25π
B． 24π
C． 20π
D． 15π
【解析】 由主视图可知圆锥的底面直径为 8，
∴底面半径 r＝4.
由左视图可知圆锥的高为 3，
∴母线长 l＝ 32＋42＝5，
∴S 圆锥侧＝πrl＝20π.
【答案】 C
【类题演练 3】 (2019·甘肃)已知某几何体的三视图如图 33-10 所示，其
的小立方体搭成，下列说法正确的是
()
A． 主视图的面积为 4
B． 左视图的面积为 4
C． 俯视图的面积为 3
D． 三种视图的面积都为 4
【答案】 A
图 33-18
4．若一个几何体的三视图如图 33-19 所示，则该几何 ( ) A． 直三棱柱 B． 长方体 C． 圆锥 D． 立方体

人教版九年级数学下册 《由三视图确定几何体的面积或体积》投影与视图PPT

人教版九年级数学下册 《由三视图确定几何体的面积或体积》投影与视图PPT

第十页，共二十二页。
新知讲解
做一做
一个机器零件的三视图如图所示(单位:cm)，这个机器 零件是一个什么样的立体图形？它的体积是多少？
15
15
10
主视图
12
左视图
解：长方体，其体积为10×12×15=1800(cm3).
第十一页，共二十二页。
10 俯视图
新知讲解
例2：如图是一个几何体的三视图，根据所示数据，求该几何体的表面积和体积.
人教版九年级数学下册 《由三视图确定几何体的面积或体积》投影与视 图PPT
科 目：数学
适用版本：人教版
适用范围：【教师教学】
由三视图确定几何体的面积或体积
九年级下册
第一页，共二十二页。
学习目标 1 会根据物体的三视图描述出基本几何体的形状；
2 会根据复杂的三视图判断实物原型.
第二页，共二十二页。
分析：由三视图可知该几何体是由圆柱、长方体组合而成.分别计算它们的表 面积和体积，然后相加即可.
第十二页，共二十二页。
新知讲解
解：该图形上、下部分分别是圆柱、长方体，根据图中数据得: 表面积为20×32π+30×40×2+25×40×2+25×30×2=(5 900+640π)(cm2),
体积为25×30×40+102×32π=(30 000+3 200π)(cm3).
主
左
视
视
13
图
图
俯 视
8
图
8
第九页，共二十二页。
新知讲解
归纳 1.三种图形的转化：
三视图
立体图
展开图
2. 由三视图求立体图形的面积的方法： （1）先根据给出的三视图确定立体图形，并确定立体图形的长、宽、高. （2）将立体图形展开成一个平面图形（展开图），观察它的组成部分. （3）最后根据已知数据，求出展开图的面积.

高中通用技术《三视图》课件

高中通用技术《三视图》课件
正投影法 三视图的形成
12/11/2021
三视图的绘制与识读
投影：在光的照射下， 形体在投影平面上产 生的影子。
投影法的分类：
12/11/2021
物体 投影面
投射中心 投射线
投影
斜投影法
正投影法
中心投影法
平行投影 法
投影法
投射线通过物体，向投影平面进行投射，并在该
面上得到图形的方法。
12/11/2021
Y
。
45
宽
对
应
相
等
H 俯视图
12/11/2021
Y
三视图之间的投影关系
1.主视图和俯视图都反映了物体的长度， 而且长对正；
2.主视图和左视图都反映了物体的高度， 而且高平齐；
3.俯视图和左视图都反映了物体的宽度， 而且宽对应相等。
这是以后画图和读图的重要依据。
12/11/2021
主视图
x
圆柱体立体投影
12/11/2021
12/11/2021
12/11/2021
V 三视图的形成
Z高
主视图从前向后看
向后翻90度
正 面 投 影 面
X长
W
左侧
o
视 图
从 左
面 投 影 面
向
右
看
H
水平投影面
12/11/2021
俯视图从上往下看
向下翻90度
Y宽
V 主视图
Z
左视图 W
X
o
Y
H 俯视图 Y
12/11/2021
三视图之间的投影关系
V 主视图
Z
左视图 W
高 平 齐
X
长对正

空间几何体的结构特征及三视图和直观图 经典课件(最新)


图 12
高中数学课件
【反思·升华】 三视图的正(主)视图、侧(左)视图、俯视图分别是从几何体的正前方、 正左方、正上方观察几何体画出的轮廓线，主视图反映了物体的长度和高度；俯视图反 映了物体的长度和宽度；左视图反映了物体的宽度和高度，由此得到：主俯长对正，主 左高平齐，俯左宽相等．
(1)由几何体的直观图画三视图需注意的事项：①注意正视图、侧视图和俯视图对应 的观察方向；②注意能看到的线用实线画，被挡住的线用虚线画；③画出的三视图要符 合“长对正、高平齐、宽相等”的基本特征；
高中数学课件
空间几何体的结构特征及三视图和直观图 课件
高中数学课件
1．空间几何体
【最新考纲】
(1)认识柱、锥、台、球及其简单组合体的结构特征，并能运用这些特征描述现实生
活中简单物体的结构．
Hale Waihona Puke (2)能画出简单空间图形(长方体、球、圆柱、圆锥、棱柱等的简易组合)的三视图，
能识别上述三视图所表示的立体模型，会用斜二侧画法画出它们的直观图．
高中数学课件
(3)旋转体的展开图 ①圆柱的侧面展开图是矩形，矩形的长(或宽)是底面圆周长，宽(或长)是圆柱的母线 长； ②圆锥的侧面展开图是扇形，扇形的半径长是圆锥的母线长，弧长是圆锥的底面周 长； ③圆台的侧面展开图是扇环，扇环的上、下弧长分别为圆台的上、下底面周长．
注：圆锥和圆台的侧面积公式 S 圆锥侧＝21cl 和 S 圆台侧＝21(c′＋c)l 与三角形和梯形的面积 公式在形式上相同，可将二者联系起来记忆．
答案：D
高中数学课件
高频考点 2 空间几何体的三视图 【例 2.1】 (2018 年高考·课标全国卷Ⅲ)中国古建筑借助榫卯将木构件连接起来，构 件的凸出部分叫榫头，凹进部分叫卯眼，图 8 中木构件右边的小长方体是榫头．若如图 摆放的木构件与某一带卯眼的木构件咬合成长方体，则咬合时带卯眼的木构件的俯视图 可以是( )

2018年秋九年级数学下册第三章三视图与表面展开图3.4简单几何体的表面展开图(3)课件(新版)浙教版

精彩练习 九年级 数学
第三章 三视图与表面展开图
3.4 简单几何体的表面展开图(3) A 练就好基础 B 更上一层楼 C 开拓新思路
A
练就好基础
1．如图所示，圆锥的侧面展开图可能是下列图中的( D )
（第1题图）
A．
B． C．
D.
2．已知圆锥的母线长为 5 cm，底面半径为 3 cm，则圆锥的表面积为( B )
考虑展开图的圆心角是否相等，由于滤纸围成的圆锥形只有最外层侧面紧贴漏斗内壁，
故只考虑该滤纸圆锥最外层的侧面和漏斗内壁圆锥侧面的关系．将圆形滤纸片按图示的
步骤折成四层且每层为14圆，则围成的圆锥形的侧面积＝1－2×41S
1 滤纸圆＝2S
， 滤纸圆
简单几何体的表面展开图(3)
第9 页
∴它的侧面展开图是半圆，其圆心角为 180°，如将漏斗内壁构成的圆锥侧面也抽象地
展开，得到的扇形弧长为 7.2π
cm，圆心角为
7.2π
÷6×180°＝216°，滤纸片如紧 π
贴漏斗壁，其围成圆锥的最外层侧面展开图的圆心角也应为 216°.
又∵重叠部分每层面积为圆形滤纸片的面积减去围成圆锥的最外层侧面展开图的面积
的差的一半，∴滤纸重叠部分每层面积＝25π －231660° °×25π ÷2＝5π (cm2)．
A．15π cm2
B．24π cm2
C．30π cm2
D．39π cm2
3．圆锥轴截面的等腰三角形的顶角为 60°，这个圆锥的母线长为 8 cm，则这个圆锥的高为
( A)
A. 4 3 cm
B．8 3 cm
C．4 cm
D．8 cm
4．如图所示，圆锥底面半径为 8，母线长为 15，则这个圆锥侧面展
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

类型
9．【中考·湖州】如图是按1：10的比例画出的一个几
何体的三视图，则该几何体的侧面积是( D )
A．200 cm2 C．100π cm2
B．600 cm2 D．200π cm2
【点拨】观察三视图知，该几何体为圆柱，高为2 cm，
底面直径为1 cm，侧面积为：πdh＝2×π＝2π(cm2)，
因为是按1:10的比例画出的三视图，所以原几何体的
类型
4．【中考·连云港】由6个大小相同的正方体搭成的几 何体如图所示，比较它的主视图，左视图和俯视 图的面积，则( C ) A．三个视图的面积一样大 B．主视图的面积最小 C．左视图的面积最小 D．俯视图的面积最小
类型
5．【中考·益阳】如图，空心卷筒纸的高度为 12 cm，外 径(直径)为 10 cm，内径为 4 cm，在比例尺为 1：4 的三视图中，其主视图的面积是( D )
示，则该几何体的体积为( A )
A．3π
B．2π
C．π
D．12π
类型
8．【中考·荆州】如图是某几何体的三视图，根据图中 的数据，求得该几何体的体积为( ) A．800π＋1 200 B．160π＋1 700 C．3 200π＋1 200 D．800π＋3 000
类型
【点拨】由三视图可知，几何体是由一个圆柱和一 个长方体组成，圆柱底面直径为20，高为8，长方体 的长为30，宽为20，高为5，故该几何体的体积为： π×102×8＋30×20×5＝800π＋3 000，故选D. 【答案】 D
1. 你虽然没有完整地回答问题，但你能大胆发言就是好样的！
此页为防盗标记页（下载后可删）
1、你的眼睛真亮，发现这么多问题！ 2、能提出这么有价值的问题来，真了不起！ 3、会提问的孩子，就是聪明的孩子！ 4、这个问题很有价值，我们可以共同研究一下！ 5、这种想法别具一格，令人耳目一新，请再说一遍好吗？ 6、多么好的想法啊，你真是一个会想的孩子！ 7、猜测是科学发现的前奏，你们已经迈出了精彩的一步！ 8、没关系，大声地把自己的想法说出来，我知道你能行！ 9、你真聪明！想出了这么妙的方法，真是个爱动脑筋的小朋友！ 10、你又想出新方法了，真会动脑筋，能不能讲给大家听一听？ 11、你的想法很独特，老师都佩服你！ 12、你特别爱动脑筋，常常一鸣惊人，让大家禁不住要为你鼓掌喝彩！ 13、你的发言给了我很大的启发，真谢谢你！ 14、瞧瞧，谁是火眼金睛，发现得最多、最快？ 15、你发现了这么重要的方法，老师为你感到骄傲！ 16、你真爱动脑筋，老师就喜欢你思考的样子！ 17、你的回答真是与众不同啊，很有创造性，老师特欣赏你这点！ 18、××同学真聪明！想出了这么妙的方法，真是个爱动脑筋的同学！ 19、你的思维很独特，你能具体说说自己的想法吗？ 20、这么好的想法，为什么不大声地、自信地表达出来呢？ 21、你有自己独特想法，真了不起！ 22、你的办法真好！考虑的真全面！ 23、你很会思考，真像一个小科学家！ 24、老师很欣赏你实事求是的态度！ 25、你的记录很有特色，可以获得“牛津奖”！
A.214π cm2
B.2116π cm2
C．30 cm2
D．7.5 cm2
【点拨】12×14＝3(cm)，10×14＝2.5(cm)，
3×2.5＝7.5(cm2)，即其主视图的面积是 7.5 cm2.故选 D.
类型
6．【中考·威海】如图是某圆锥的主视5π B．24π
1. 说得太好了，老师佩服你，为你感到骄傲！ 2. 你的设计(方案、观点)富有想象力，极具创造性。 3. 我非常欣赏你的想法，请说具体点，好吗? 4. 某某同学的解题方法非常新颖，连老师都没想到，真厉害！ 5. 让我们一起为某某喝彩！同学们在学习过程中，也要敢于猜想，善于猜想，这样才能有所发现，有所创造! 三、表扬类
C．20π D．15π
【点拨】根据圆锥的主视图、左视图知，该圆锥的轴截面是一
个底边长为 8，高为 3 的等腰三角形，如图，过点 A 作 AC⊥
BD 于点 C，则 BC＝12BD＝4.∴AB＝ 32＋42＝5，
圆锥底面周长为 8π，∴侧面积＝12×8π×5＝20π.
类型
7．某几何体的主视图、左视图和俯视图分别如图所
1、“读”是我们学习语文最基本的方法之一，古人说，读书时应该做到“眼到，口到，心到”。我看，你们今天达到了这个要求。 2、大家自由读书的这段时间里，教室里只听见琅琅书声，大家专注的神情让我感受到什么叫“求知若渴”，我很感动。 3、经过这么一读，这一段文字的意思就明白了，不需要再说明什么了。 4、请你们读一下，将你的感受从声音中表现出来。 5、读得很好，听得出你是将自己的理解读出来了。特别是这一句，请再读一遍。
探究培优
(3)计算制作一个这样的纸盒所需纸板的面积．(结果精
确到个位) 解：由三视图可知该几何体的上、下底面是边长为 5 cm
的正六边形，侧面是 6 个边长为 5 cm 的正方形，则该
几何体的表面积为 6×52× 43×2＋6×5×5＝75 75( 3＋2)≈280(cm2)．
3＋150＝
同学们下课啦
(3)如果要给这个模型刷油漆，每千克油漆可以漆4 m2， 需要油漆多少千克？ 模型的表面积＝2×3×2＋2×1.5×2＋10×5×2＋ 5×6×2＋6×10×2＝298(m2)， 需要油漆298÷4＝74.5(kg)．
探究培优
13．如图是一个包装纸盒的三视图．(单位：cm) (1)该包装纸盒的几何形状是__正__六__棱__柱____； (2)画出该纸盒的表面展开图； 解：如图．(答案不唯一)
整合方法
11．某直三棱柱零件如图①，张师傅根据此零件按1：1的 比例画出准确的三视图如图②.已知在△EFG中，EF ＝4 cm，∠EFG＝45°，FG＝12 cm，又知AD＝8 cm.
(1)求AB的长； 解：过点 E 作 EH⊥FG 于点 H，如图． 在 Rt△EHF 中，EF＝4 cm，∠EFH＝45°， ∴EH＝EF·sin ∠EFH＝4×sin 45°＝2 2(cm)． 由图形可知 AB＝EH＝2 2 cm.
侧面积＝100×2π＝200π(cm2)，故选D.
整合方法
10．如图为一几何体从不同方向看到的图形． (1)写出这个几何体的名称；
解：正三棱柱．
整合方法
(2)任意画出这个几何体的一种表面展开图； 【点拨】答案不唯一．
解：如图．
(3)若长方形的长为10 cm，正三角形的边长 为4 cm，求这个几何体的侧面积． 10×4×3＝120(cm2)．
类型
1．如图是某几何体的三视图，则该几何体的侧 面展开图是( A )
类型
2．如图是一个几何体的展开图，下面哪个平面图形不 是它的三视图中的一个视图( D )
类型
3．如图是三个物体的三视图和展开图，请将同一物体 的三视图和展开图搭配起来．
A与____c____，B与____a____，C与____b____．
授课老师：xxx
此页为防盗标记页（下载后可删）
教师课堂用语在学科专业方面重在进行“引”与“导”，通过点拨、搭桥等方式让学生豁然开朗，得出结论，而不是和盘托 出，灌输告知。一般可分为：启发类、赏识类、表扬类、提醒类、劝诫类、鼓励类、反思类。
一、启发类
1. 集体力量是强大的，你们小组合作了吗?你能将这个原理应用于生活吗?你的探究目标制定好了吗? 2. 自学结束，请带着疑问与同伴交流。 3. 学习要善于观察，你从这道题中获取了哪些信息? 4. 请把你的想法与同伴交流一下，好吗? 5. 你说的办法很好，还有其他办法吗?看谁想出的解法多? 二、赏识类
LJ版九年级上
第四章 投影与视图
2视 图 第3课时 由三视图到几何体的展开图
习题链接
提示：点击 进入习题
1A 2D 3 c；a；b 4C
5D 6C 7A 8D
答案显示
习题链接
提示：点击 进入习题
9D 10 见习题 11 (1)2 2 cm.(2)96 2(cm3)． 12 见习题 13 见习题
答案显示
整合方法
(2)求出这个直三棱柱的体积．
解：直三棱柱的体积＝S△EFG· AD＝12×12×2 2×8＝96 2(cm3)．
探究培优
12．已知一个模型的三视图如图所示．(单位：m) (1)请描述这个模型的形状．
解：此模型由两个长方体组成： 上面是一个小长方体，下面是一 个大长方体．
探究培优
(2)制作这个模型的木料密度为360 kg/m3，则这个模型的 质量是多少千克？ 解：模型的体积＝5×6×10＋2×3×1.5＝309(m3)， 则该模型的质量＝309×360＝111 240(kg)．
1. 你真让人感动，老师喜欢你的敢想、敢说、敢问和敢辩，希望你继续保持下去。 2. 这么难的题你能回答得很完整，真是了不起！你是我们班的小爱因斯坦。 3. 你预习的可真全面，自主学习的能力很强，课下把你的学习方法介绍给同学们，好不好？ 4. 哎呀. 通过你的发言，老师觉得你不仅认真听，而且积极动脑思考了，加油哇！ 四、提醒类
此页为防盗标记页（下载后可删）
1、谢谢大家听得这么专心。 2、大家对这些内容这么感兴趣，真让我高兴。 3、你们专注听讲的表情，使我快乐，给我鼓励。 4、我从你们的姿态上感觉到，你们听明白了。 5、我不知道我这样说是否合适。 6、不知我说清了没有，说明白了没有。 7、我的解释不知是否令你们满意，课后让我们大家再去找有关的书来读读。 8、你们的眼神告诉我，你们还是没有明白，想不想让我再讲一遍？ 9、会“听”也是会学习的表现。我希望大家认真听好我下面要说的一段话。 10、从听课的情况反映出，我们是一个素质良好的集体。 1、谢谢你，你说的很正确，很清楚。 2、虽然你说的不完全正确，但我还是要感谢你的勇气。 3、你很有创见，这非常可贵。请再响亮地说一遍。 4、××说得还不完全，请哪一位再补充。 5、老师知道你心里已经明白，但是嘴上说不出，我把你的意思转述出来，然后再请你学说一遍。 6、说，是用嘴来写，无论是一句话，还是一段话，首先要说清楚，想好了再说，把自己要说的话在心里整理一下就能说清楚。 7、对！说得很好，我很高兴你有这样的认识，很高兴你能说得这么好！ 8、我们今天的讨论很热烈，参与的人数也多，说得很有质量，我为你们感到骄傲。 9、说话，是把自己心里的想法表达出来，与别人交流。说时要想想，别人听得明白吗？ 10、说话，是与别人交流，所以要注意仪态，身要正，不扭动，眼要正视对方。对！就是这样！人在小时候容易纠正不良习惯，经常 注意哦。