第五版普通物理11-4,11-5安培环路定理及其应用汇总
- 格式:doc
- 大小:1.33 MB
- 文档页数:15





大学普通物理(第五版)目录(程守洙)第一篇力学第一章质点的运动§1.1质点参考系运动方程§1.2位移速度加速度§1.3圆周运动及其描述§1.4曲线运动方程的矢量形式§1.5运动描述的相对性伽利略坐标变换第二章牛顿运动定律第二章牛顿运动定律§2.1牛顿第一定律和第三定律§2.2常见力和基本力§2.3牛顿第二定律及其微分形式§2.4牛顿运动定律应用举例§2.5牛顿第二定律积分形式之一:动量定理§2.6牛顿第二定律积分形式之二:动能定理§2.7非惯性系惯性力阅读材料A 混沌和自组织现象第三章运动的守恒定律第三章运动的守恒定律§3.1保守力成对力作功势能§3.2功能原理§3.3机械能守恒定律能量守恒定律§3.4质心质心运动定理动量守恒定律火箭飞行§3.5碰撞§3.6质点的角动量和角动量守恒定律§3.7质点在有心力场中的运动§3.8对称性和守恒定律阅读材料B 宇宙的膨胀第四章刚体的转动第四章刚体的运动§4.1刚体的平动、转动和定轴转动§4.2刚体的角动量转动动能转动惯量§4.3 力矩刚体定轴转动定律§4.4定轴转动的动能定理§4.5刚体的自由度刚体的平面平行运动§4.6定轴转动刚体的角动量定理和角动量守恒定律§4.7进动第五章相对论基础第五章相对论基础§5.1伽利略相对性原理经典力学的时空观§5.2狭义相对论基本原理洛伦兹坐标变换式§5.3相对论速度变换公式§5.4狭义相对论时空观§5.5狭义相对论动力学基础§5.6广义相对论简介阅读材料C 超新星爆发和光速不变性第六章气体动理论第二篇热学第六章气体动理论§6.1 状态过程理想气体§6.2分子热运动和统计规律§6.3气体动理论的压强公式§6.4理想气体的温度公式§6.5能量均分定理理想气体的内能§6.6麦克斯韦速率分布律§6.7玻尔兹曼分布律重力场中粒子按高度的分布§6.8分子的平均碰撞次数及平均自由程§6.9气体内的迁移现象§6.10真实气体范德瓦耳斯方程§6.11物态和相变阅读材料D 非常温和非常压第七章热力学基础第七章热学基础§7.1热力学第一定律§7.2热力学第一定律对于理想气体等值过程的应用§7.3绝热过程多方过程§7.4焦耳-汤姆孙实验真实气体的内能§7.5循环过程卡诺循环§7.6热力学第二定律§7.7可逆过程与不可逆过程卡诺定理§7.8熵§7.9熵增加原理热力学第二定律的统计意义阅读材料E 熵与能源第三篇电场和磁场第八章真空中的静电场§8-1 电荷库仑定律§8-2 电场电场强度§8-3 高斯定理§8-4 静电场的环路定理电势§8-5 等势面电场强度与电势梯度的关系§8-6 带电粒子在静电场中的运动阅读材料F电子的发现和电子电荷量的测定第九章导体和电介质中的静电场§9-1 静电场中的导体§9-2 空腔导体内外的静电场§9-3 电容器的电容§9-4 电介质及其极化§9-5 电介质中的静电场§9-6 有电介质时的高斯定理电位移§9-7 电场的边值关系§9-8 电荷间的相互作用能静电场的能量§9-9 铁电体压电体永电体阅读材料G静电现象的应用第十章恒定电流和恒定电场§10-1 电流密度电流连续性方程§10-2 恒定电流和恒定电场电动势§10-3 欧姆定律焦耳一楞次定律§10-4 一段含源电路的欧姆定律。





安培环路定理的原理及应用1. 安培环路定理的原理安培环路定理是电磁学中的基本定理之一,它描述了电流通过一个封闭路径的总和等于该路径上环绕的总磁场的空间积分。
安培环路定理是麦克斯韦方程组中的一部分,对于理解和分析电路中的电磁现象非常重要。
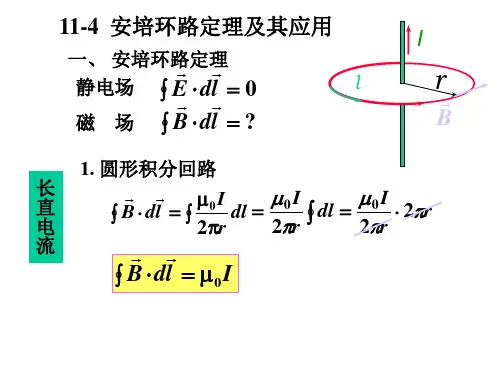
根据安培环路定理,一个封闭路径上的环绕磁场的空间积分等于该路径上的电流的总和乘以真空中的磁导率常数,即:$$\\oint \\vec{B} \\cdot \\vec{dl} = \\mu_0 \\cdot I_{\\text{enc}}$$其中, - $\\vec{B}$ 表示磁场的矢量 - $\\vec{dl}$ 表示路径上的无穷小位移矢量 - $\\mu_0$ 是真空中的磁导率常数 - $I_{\\text{enc}}$ 表示通过封闭路径所包围的电流的总和2. 安培环路定理的应用2.1 电磁铁电磁铁是利用安培环路定理工作的重要装置之一。
在电磁铁中,通电线圈产生的磁场可以吸引或排斥物体,从而实现各种实际应用。
根据安培环路定理,我们可以通过改变通电线圈中的电流大小来控制磁场的强度,进而达到对物体的吸引或排斥。
2.2 变压器变压器也是应用安培环路定理的重要设备。
变压器是一种用于改变交流电压的装置,它由两个共用一个磁路的线圈构成。
输入线圈(原线圈)中的交流电流通过变压器的磁场感应出感应电动势,进而产生在输出线圈上的输出电压。
安培环路定理被用于分析和计算变压器中的磁场和电流之间的关系。
2.3 电感与电感耦合安培环路定理在电感和电感耦合的研究和应用中也起到了重要作用。
电感是一种储存电能的元件,当电流通过电感时,会在其周围产生磁场。
根据安培环路定理,我们可以得到电感中的磁场与电流的关系,从而进一步分析和设计电感相关的电路。
而电感耦合是指通过电感的互相感应,将两个或多个电路联系起来。
在电感耦合的应用中,安培环路定理可用于计算和描述各个电路之间的电磁相互作用,以及电感耦合的性能与参数之间的关系。
第五版普通物理习题 11-4,11-5安培环路定理及其应用1.选择题1若空间存在两根无限长直载流导线,空间的磁场分布就不具有简单的对称性,则该磁场分布(A )不能用安培环路定理来计算 (B )可以直接用安培环路定理求出 (C )只能用毕奥-萨伐尔定律求出(D )可以用安培环路定理和磁感应强度的叠加原理求出[ ]答案:(D )2在图(a )和(b )中各有一半径相同的圆形回路L 1和L 2,圆周内有电流I 1和I 2,其分布相同,且均在真空中,但在(b )图中L 2回路外有电流I 3,P 2、P 1为两圆形回路上的对应点,则:(A )2121,P P L L B B l d B l d B =⋅=⋅⎰⎰ (B )2121,P P L L B B l d B l d B ≠⋅≠⋅⎰⎰(C )2121,P P L L B B l d B l d B ≠⋅=⋅⎰⎰ (D )2121,P P L L B B l d B l d B =⋅≠⋅⎰⎰[ ]答案:(C )3一载有电流I 的导线分别均匀密绕在半径为R 和r 的长直圆筒上形成两个螺线管(R=2r ),两螺线管单位长度上的匝数相等,两螺线管中的磁感应强度大小B R 和B r 应满足(A )B R =2B r (B )B R =B r (C )2B R =B r (D )B R =4B r [ ] 答案:(B )4无限长载流空心圆柱导体的内外半径分别为a 、b ,电流在导体截面上均匀分布,则空间各处的B的大小与场点到圆柱中心轴线的距离r 的关系定性地如图所示。
正确的图是(A) (B) (C) (D)[ ] 答案:(B)5如图所示,六根无限长导线互相绝缘,通过电流均匀为I,区域Ⅰ、Ⅱ、Ⅲ、Ⅳ均为相等的正方形,哪一个区域指向纸内的磁通量最大(A)Ⅰ区域(B)Ⅱ区域(C)Ⅲ区域(D)Ⅳ区域[ ]答案:(B)6如图所示,流出纸面的电流为2I,流进纸面的电流为I,则下述式中哪一个是正确的(A)Il dBL12μ=⋅⎰(B)Il dBL2μ=⋅⎰(C)Il dBL3μ-=⋅⎰(D)Il dBL4μ-=⋅⎰[ ] 答案:(D)7在一圆形电流I所在的平面内,选取一个同心圆形闭合回路L,则由安培环路定理可知(A)0=⋅⎰l dBL,且环路上任意一点B=0(B)0=⋅⎰l dBL,且环路上任意一点B≠0(C)0≠⋅⎰l dBL,且环路上任意一点B≠0(D)0≠⋅⎰l dBL,且环路上任意一点B=常量[ ]8如图,两根直导线ab 和cd 沿半径方向被接到一个截面处处相等的铁环上,稳恒电流I 从a 端流入而从d 端流出,则磁感强度B 沿图中包围铁环截面的闭合路径L 的积分ld B L⋅⎰等于(A )I 0μ (B )3/0I μ (C )4/0I μ (D )3/20I μ[ ]答案:D9无限长直圆柱体,半径为R ,沿轴向均匀流有电流。
第五版普通物理习题 11-4,11-5安培环路定理及其应用1.选择题1若空间存在两根无限长直载流导线,空间的磁场分布就不具有简单的对称性,则该磁场分布(A )不能用安培环路定理来计算 (B )可以直接用安培环路定理求出 (C )只能用毕奥-萨伐尔定律求出(D )可以用安培环路定理和磁感应强度的叠加原理求出[ ]答案:(D )2在图(a )和(b )中各有一半径相同的圆形回路L 1和L 2,圆周内有电流I 1和I 2,其分布相同,且均在真空中,但在(b )图中L 2回路外有电流I 3,P 2、P 1为两圆形回路上的对应点,则:(A )2121,P P L L B B l d B l d B =⋅=⋅⎰⎰ (B )2121,P P L L B B l d B l d B ≠⋅≠⋅⎰⎰(C )2121,P P L L B B l d B l d B ≠⋅=⋅⎰⎰ (D )2121,P P L L B B l d B l d B =⋅≠⋅⎰⎰[ ]答案:(C )3一载有电流I 的导线分别均匀密绕在半径为R 和r 的长直圆筒上形成两个螺线管(R=2r ),两螺线管单位长度上的匝数相等,两螺线管中的磁感应强度大小B R 和B r 应满足(A )B R =2B r (B )B R =B r (C )2B R =B r (D )B R =4B r [ ] 答案:(B )4无限长载流空心圆柱导体的内外半径分别为a 、b ,电流在导体截面上均匀分布,则空间各处的B的大小与场点到圆柱中心轴线的距离r 的关系定性地如图所示。
正确的图是(A) (B) (C) (D)[ ] 答案:(B)5如图所示,六根无限长导线互相绝缘,通过电流均匀为I,区域Ⅰ、Ⅱ、Ⅲ、Ⅳ均为相等的正方形,哪一个区域指向纸内的磁通量最大(A)Ⅰ区域(B)Ⅱ区域(C)Ⅲ区域(D)Ⅳ区域[ ]答案:(B)6如图所示,流出纸面的电流为2I,流进纸面的电流为I,则下述式中哪一个是正确的(A)Il dBL12μ=⋅⎰(B)Il dBL2μ=⋅⎰(C)Il dBL3μ-=⋅⎰(D)Il dBL4μ-=⋅⎰[ ] 答案:(D)7在一圆形电流I所在的平面内,选取一个同心圆形闭合回路L,则由安培环路定理可知(A)0=⋅⎰l dBL,且环路上任意一点B=0(B)0=⋅⎰l dBL,且环路上任意一点B≠0(C)0≠⋅⎰l dBL,且环路上任意一点B≠0(D)0≠⋅⎰l dBL,且环路上任意一点B=常量[ ]8如图,两根直导线ab 和cd 沿半径方向被接到一个截面处处相等的铁环上,稳恒电流I 从a 端流入而从d 端流出,则磁感强度B 沿图中包围铁环截面的闭合路径L 的积分ld B L⋅⎰等于(A )I 0μ (B )3/0I μ (C )4/0I μ (D )3/20I μ[ ]答案:D9无限长直圆柱体,半径为R ,沿轴向均匀流有电流。
设圆柱体内(r<R )的磁感强度为i B ,圆柱体外(r>R )的磁感强度为e B ,则有(A )i B 、e B 均与r 成正比 (B )i B 、e B 均与r 成反比(C )i B 与r 成反比,e B 与r 成正比 (D )i B 与r 成正比,e B 与r 成反比[ ]答案:(D )10若使半径为4⨯103-m 的裸铜线表面的磁感强度为5100.7-⨯T ,则铜线中需要通过的电流为(A )0.14 A (B )1.4 A (C )2.8 A (D )14 A [ ] 答案:B11取一闭合积分回路L ,使三根载流导线穿过它所围成的面。
现改变三根导线之间的相互间隔,但不越出积分回路,则(A )回路L 内的∑I 不变,L 上各点的B不变 (B )回路L 内的∑I 不变,L 上各点的B改变 (C )回路L 内的∑I 改变,L 上各点的B不变(D )回路L 内的∑I 改变,L 上各点的B 改变 [ ]12磁场由沿空心长圆筒形导体的均匀分布的电流产生,圆筒半径为R,X坐标轴垂直圆筒轴线,原点在中心轴线上,图(A )~(D )哪一条曲线表示B~X的关系?[ ]答案:(B )13下列结论中你认为正确的是 (A )一根给定磁感应线上各点的B 的量值相同(B )用安培环路定理可以求出有限长一段直线电流周围的磁场(C )B的方向是运动电荷所受磁力最大的方向(或试探载流线圈所受力矩最大的方向) (D )一个不为零电流元在它的周围空间中任一点产生的磁感应强度也均不为零[ ]答案:(D) 14(A )有限长载流直导体 (B )(C )有限长载流螺线管 (D )无限长螺线管 [ ] 答案:(D)2. 判断题:1可用安培环路定律推导出毕奥-萨伐尔定律。
( ) 答案:错2只有电流分布具有某种对称性时,才可用安培环路定理求解磁场问题。
( ) 答案:对3对于多个无限长平行载流直导线的磁场问题,由于总的磁场强度不具备对称性,求解过程中不可用安培环路定理。
( )答案:错4对于有限长、断面是圆形的载流直导线的磁场问题,由于圆形断面具有对称性,所以可用安培环路定理来求解此导线在周围产生的磁场。
( )答案:错5对于圆形载流螺线管,当螺线管只有一层密绕线圈时,由于单位长度上的电流密度相同,而且螺线管具有某些几何对称性,所以可用安培环路定理来求出螺线管两端的磁场。
( )答案:错6对于螺绕环,只有当环的孔径比环的平均半径小得多时,才可用安培环路定理来求解环内的磁场。
( )答案:错7对于载流螺线管内部,中部的磁感应线比两端的多。
( ) 答案:对8闭合曲线当中没有包含电流,说明闭合曲线中的磁感应强度处处为零。
( ) 答案:错3. 填空题1若通过S 面上某面元S d的元磁通为d ϕ,而线圈中的电流增加为2I 时,通过同一面元的元磁通为φ'd ,则d ϕ:φ'd =答案:1:22,S 是一流有恒定电流的闭合线圈,电流强度为I ,方向如图,试求磁感应强度沿闭合曲线的环路积分⎰⋅l d B为 。
答案:I 02μ-3一根很长的圆形螺线管,沿圆周方向的面电流密度为i ,在线圈内部的磁感应强度为 。
答案:i 0μ4一根很长的螺线管,总电阻20欧姆,两端连接在12V 的电源上,线圈半径2cm ,线圈匝数200匝/厘米,在线圈内部距离轴线0.01m 处的磁场强度为 。
答案:3108.4-⨯π T5如图所示,半径为5.0cm 的无限长直导线直圆柱形导体上,沿轴线方向均匀地流着3=I A 的电流。
作一个半径为5=r cm ,长5=l cm 且与电流同轴的圆柱形闭合曲面S ,则该曲面上的磁感强度B沿曲面的积分为 。
答案:06一无限长直圆筒,半径为R ,表面带有一层均匀电荷,面密度为σ,在外力矩的作用下,圆筒从0=t 时刻开始以匀角加速度β绕轴转动,在t 时刻圆筒内离轴为r 处的磁感 应强度大小为 。
答案:t R βσμ07一无限长直圆筒,半径为R ,表面带有一层均匀电荷,面密度为σ,以匀角速度ω 绕轴转动,在圆筒内的磁感应强度大小为 。
答案: σωμR 04. 计算题1一根很长的同轴电缆,由一导体圆柱和一同轴的圆筒组成,设圆柱的半径为1R ,圆筒的内外半径为2R 和3R 。
在这两个导体中,有大小相等而方向相反的电流I 流过,如图。
试求电缆产生的磁场磁感强度的分布,并用图形表示。
解: 在电缆的横截面内,以圆柱的轴为圆心,作不同半径的圆为环路。
利用安培环路定理,可求得不同场点的磁感强度。
(1)当1R r <时,有I R r r B l d B ⎰=⋅=⋅21202ππμπ , 2102R Ir B πμ= (2分) (2)当21R r R <<时,有I r B l d B ⎰=⋅=⋅02μπ ,rIB πμ20= (2分) (3)当32R r R <<时[]⎰⎥⎥⎦⎤⎢⎢⎣⎡---=⋅=⋅I R R R r I r B l d B 22232220)(2ππμπ , 222322302R R r R r I B --=πμ (2分) (4)当3R r >时⎰=-=⋅=⋅0)(20I I r B l d B μπ,0=B (2分)B-r 的关系如图所示。
(2分)2一多层密绕螺线管,内半径为1R ,外半径为长为2R ,长为l ,如图所示。
设总匝数012I R μπ022I R μπ为N ,导线中通过的电流为I 。
试求这螺线管中心O 点的磁感强度。
解 在螺线管中取一原为dr 的密绕导线薄层,由螺线管磁场计算公式,得该薄层在其中心O 点的磁感强度θμθθμcos )cos (cos 20120ni ni dB =-=(3分)其中n 为单位长度的匝数,则有dr lR R Nn )(12-=,22)2(2cos l r l +=θ代入得2212022120)2()(2)2(2)(l r dr R R NI l r l drlR R NIdB +-=+-=μμ (3分)整个螺线管在O 点产生的磁感强度2211222212022120)2()2(ln)(2)2()(221l R R l R R R R NI l r dr R R NI dB B R R ++++-=+-==⎰⎰μμ(3分)3一均匀带电长直圆柱体,电荷体密度为ρ,半径为R ,绕其轴线匀速转动,角速度为w 试求:(1)圆柱体内距轴线r 处的磁感强度 (2)两端面中心处的磁感强度解 (1)体内均匀带电的长直圆柱体以角速度w 旋转时,等效为一个多层的同轴密绕螺线管。
在管外,r>R 处,B =0。
在管内距轴线r 处,作如图所示的积分回路,由安培环路定理得I dl ∆=⋅⎰0μB (2分)而πρπ2)(22wlr R I ∆-=∆,代入得 )(21220r R w B -=ρμ (2分) 将r=0代入,得中心轴线的磁感强度2021R w B ρμ=(3分) (2)端面中心处的磁感强度为中心轴线处的一半,即2041R w B ρμ= (3分)4一无限大均匀载流平面置于外磁场中,左侧的磁感强度为1B ,右侧的磁感强度为123B B =,方向如图所示。
试求:(1)载流平面上的面电流密度; (2)外磁场的磁感强度0B解(1)作闭合回路abcda ,由安培环路定理得l j l B Bl B l B dl ∆=∆-=∆-∆=∙⎰01112)3(μB (2分)所以012μB j =方向垂直纸面向外。
(2分)(2)面电流产生的磁场,在右边磁感强度的方向沿z 轴正向,左边沿z 轴负向,量值是j B 0'21μ=。
(1分) 设外磁场为k B j B i B B z y x0000++=,由场强叠加原理:'B B B 02 +=,即k j k B j B i B k B z y x00001213μ+++= (2分)所以00=x B ,00=y B ,10101022213B BB k B z =-=μμ即102B B =方向沿z 轴正向。