安培环路定理

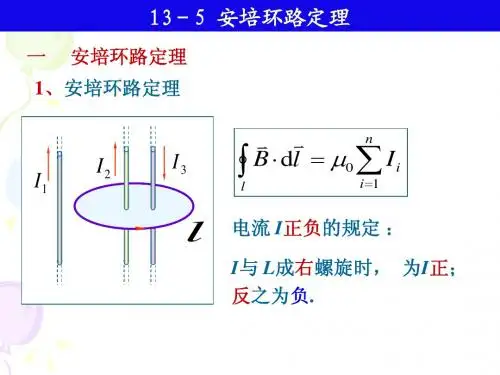
安培环路定理
安培环路定理的严格证明(缩略图)
在稳恒磁场中，磁场强度H沿任何闭合路径的线积分，等于这闭合路径所包围的各个电流之代数和。

这个结论称为安培环路定理（Ampere circuital theorem）。

安培环路定理可以由毕奥－萨伐尔定律导出。

它反映了稳恒磁场的磁感应线和载流导线相互套连的性质。

目录
按照安培环路定理，环路所包围电流之正负应服从右手螺旋法则。

安培环路定理应用
如果闭合路径l包围着两个流向相反的电流I1和I2（如左图所示），这在下式中，
按图中选定的闭合路径l 的绕行方向，B矢量沿此闭合路径的环流为如果闭合路径l包围的电流等值反向（如右图所示），或者环路中并没有包围电流，则：
安培环路定理的证明(严格证明,大图见参考资料的链接)
编辑本段安培环路定理的证明（不完全证明）
以长直载流导线产生的磁场为例，证明安培环路定理的正确性。

安培环路定理应用
在长直载流导线的周围作三个不同位置，且不同形状的环路，可以证明对磁场中这三个环路，安培环路定理均成立。

取对称环路包围电流
在垂直于长直载流导线的平面内，以载流导线为圆心作一条半径为r 的圆形环路l，
则在这圆周上任一点的磁感强度H的大小为
其方向与圆周相切．取环路的绕行方向为逆时针方向，取线元矢量dl，则H与dl间的夹角，H沿这一环路 l 的环流为
式中积分是环路的周长。

于是上式可写成为
从上式看到，H沿此圆形环路的环流只与闭合环路所包围的电流I 有关，而与环路的大小、形状无关。

取任意环路包围电流
在垂直于长直载流导线的平面内，环绕载流直导线作一条如下图所示的任意环路l，取环路的绕行方向为逆时针方向。

在环路上任取一段线元dl，载流直导线在线元dl处的磁感强度B大小为
H与dl的夹角为，则H对dl的线积分为
直导线中心向线元的张角为，则有，所以有
可见，H对dl的线积分与到直导线的距离无关。

那么B对整个环路的环流值为
上述计算再次说明H的环流值与环路的大小、形状无关。

取任意环路不包围电流
在垂直于长直载流导线的平面内，在载流直导线的外侧作一条如下图所示的任
安培环路定理应用
意环路l，取环路的绕行方向为逆时针方向。

以载流直导线为圆心向环路作两条夹角为的射线，在环路上截取两个线元和。

和距直导线圆心的距离分别为和，直导线在两个线元处的磁感强度分别为和。

从上图可以看出，而。

利用安培环路定理的证明之二的结论可知
结论
所以有
从载流直导线中心O出发，可以作许多条射线，将环路分割成许多成对的线元，磁感强度对每对线元的标量积之和，都有上式的结果，故即环路不包围电流时，B的环流值为零。

安培环路定理反映了磁场的基本规律。

和静电场的环路定理相比较，稳恒磁场中B 的环流，说明稳恒磁场的性质和静电场不同，静电场是保守场，稳恒磁场是非保守场。

安培环路定理应用
可以找到一条闭合环路l，该环路上的磁感强度B大小处处相等，B的方向和环路的绕行方向也处处同向，这样利用安培环路定理求磁感强度B的问题，就转化为求环路长度，以及求环路所包围的电流代数和的问题，即利用安培环路定理求磁场的适用范围：在磁场中能否找到上述的环路，取决于该磁场分布的对称性，而磁场分布的对称性又来源于电流分布的对称性。

因此，只有下述几种电流的磁场，才能够利用安培环路定理求解。

1.电流的分布具有无限长轴对称性
2.电流的分布具有无限大面对称性
3.各种圆环形均匀密绕螺绕环
编辑本段利用安培环路定理求磁场的基本步骤
1.首先用磁场叠加原理对载流体的磁场作对称性分析；
2.根据磁场的对称性和特征，选择适当形状的环路；
3.利用公式（1）求磁感强度。

简介
用磁场叠加原理作对称性分析：可将长直密绕载流螺线管看作由无穷多个共轴
安培环路定理应用
的载流圆环构成，其周围磁场是各匝圆电流所激发磁场的叠加结果。

在长直载流螺线管的中部任选一点P，在P点两侧对称性地选择两匝圆电流，由圆电流的磁场分布可知，二者磁场叠加的结果，磁感强度B的方向与螺线管的轴线方向平行。

由于长直螺线管可以看成无限长，因此在P点两侧可以找到无穷多匝对称的圆电流，它们在P点的磁场迭加结果与上图相似。

由于P点是任选的，因此可以推知长直载流螺线管内各点磁场的方向均沿轴线方向。

磁场分布如下图所示。

从上图可以看出，在管内的中央部分，磁场是均匀的，其方向与轴线平行，并可按右手螺旋法则判定其指向；而在管的中央部分外侧，磁场很微弱，可忽略不计，即H=0．
利用安培环路定理可以解得螺线管内的磁感强度为
具体解的过程
根据长直载流螺线管中段的磁场分布特征，可以选择如下图所示的矩形环路及绕行方向。

则环路ab段的dl方向与磁场B的方向一致，即；环路bc段和da段的dl方向与磁场B的方向垂直，即B·dl =0；环路cd段上的。

于是，沿此闭合路径l，磁感强度B的环流为:
因为ab段的磁场是均匀的，可以从积分号中提出，则上式成为:
设螺线管上每单位长度有n匝线圈，通过每匝的电流是I，则闭合路径所围绕的总电流为nI，根据右手螺旋法则，其方向是正的。

按安培环路定理，有:
注意对于绕得不紧的载流螺线管，其磁场的分布就不是如此。

对于绕得不紧的均匀载流螺线管，由下图可以看到，在靠近导线处的磁场和一条长直载流导线附近的磁场很相似，磁感线近似为围绕导线的一些同心圆。

管内、外的磁场是不均匀的，仅在螺线管的轴线附近，磁感强度B的方向近乎与轴线平行。

简介
对于如图所示的均匀密绕螺绕环，由于整个电流的分布具有中心轴对称性，因而磁场的分布也应具有轴对称性，因此，利用安培环路定理可以解得均匀密绕螺绕环内部的磁场分布为
具体解的过程
将通有电流I 的矩形螺绕环沿直径切开，其剖面图如下所示。

在环内作一个半径为r 的环路，绕行方向如图所示。

环路上各点的磁感强度大小相等，方向由右手螺旋法可知：与环路绕行方向一致。

磁感强度B沿此环路的环流为
环路内包围电流的代数和为。

根据安培环路定理，有:
对均匀密绕螺绕环，环上的线圈绕得很密，则磁场几乎全部集中于管内，在环的外部空间，磁感强度处处为零，即B =0。

如果将长直载流螺线管对接起来，就形成了圆形截面的均匀密绕细螺绕环，由安培环路定理同样可以解得其内部的磁场和长直载流螺线管内部的磁场相同，仍为。

•1
<<电动力学>> 虞福春郑春开编著北京大学出版社
•2
•3
/1dxwl/d关于毕奥、沙法尔定律的颠覆性研究，是朱昱昌关于电磁学基础理论研究的新成果。

朱昱昌的《关于螺线管内轴线磁场的探讨》、《关于安培环路定理的探讨》）、《试论螺线管结构特征和磁场分布》、《试论螺线管的隧道屏蔽效应》等4篇论文，分析透彻，反例鲜明而具体，读后会让人耳目一新，茅塞顿开！请快快访问
•4
新浪博客：http///yuzheyiding •5
•6
3pdx/11.3.htm。