倍长中线法(加倍法)PPT课件

中线的妙用-针对对象：初二学生-期末分值：8~10分学习目标-2013·台州市中考在△ABC中，AD为BC边上的中线-且AD平分∠BAC,则△ABC为-三角形。

造全等一一倍长中线法-B-倍长中线造法：延长AD到点E,使得AD=DE,连结BE或者EC。

-全等原因：SAS-注意：往左往右都可以，只连一条。

-2 20/5/24题型识别：-【例1】如图AD是△ABC的中线，求证AB+AC>2AD-出现中线-证明：延长AD到点E,使得AD=DE,-口诀：-连结BE。

-倍长中-.AD是△ABC的中线-∵BD=DC-步骤：-C·.BD=DC,∠BDE=∠ADC,-延长一倍-.△ADC≌△BDESAS-构造全等-∴.AC=E,∠E=∠1，∠EBD=∠C-边角关系-三角形两边之和大于第三边-·.AB+BE>AE-∴.AB+AC>2AD题型识别：-s【例2】如图在ABC,AB=5,AC=3,则中线AD-出现中线-的取值范围是？-口诀：-接上题，BE=AC=3,AB+AC>2AD-长中线-·三角形两边之差小于第三边-步骤：-..AB-BE<AE-延长一倍-C.·AB-BE<2AD-构造全-..AB-BE<2AD<AB+BE-角关系-..2<2AD<8-.1<AD<4题型识别：-【例3】如图在ABC,AC=5,中线AD=7,则AB边-出现中线-的取值范围是？-口诀：-接例1，BE=AC=5,-倍长中线-AE=2 D-14-步骤：-延长一倍-C·在△ABE中-构造全-AE-BE<AB<AE+BE-边角关系-.9<AB<19【例4】如图在△ABC,AB=AC,延长AB到D,使得BD=-题型识别：-出现中线-AB,取AB的中点E,连结CD和CE,求证CD=2CE。

-证明延长AE到点F,使得CE=EF,连结BF。

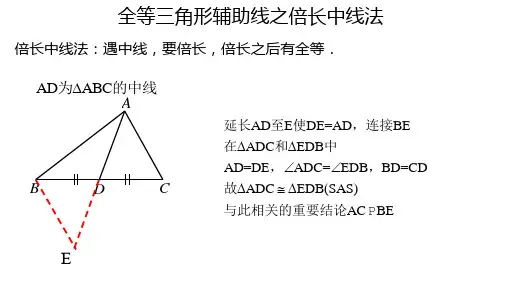
倍长中线法（加倍法）知识网络详解：中线是三角形中的重要线段之一，在利用中线解决几何问题时，常常采用“倍长中线法”添加辅助线．所谓倍长中线法，就是将三角形的中线延长一倍，以便构造出全等三角形，从而运用全等三角形的有关知识来解决问题的方法．倍长中线法的过程：延长某某到某点，使某某等于某某，使什么等于什么（延长的那一条），用SAS证全等（对顶角）倍长中线最重要的一点，延长中线一倍，完成SAS全等三角形模型的构造。

经典例题讲解：例1：△ABC中，AB=5，AC=3，求中线AD的取值范围。

例2：已知在△ABC中，AB=AC，D在AB上，E在AC的延长线上，DE交BC于F，且DF=EF，求证：BD=CE例3：已知在△ABC 中，AD 是BC 边上的中线，E 是AD 上一点，且BE=AC ，延长BE 交AC 于F ，求证：AF=EF例4：如图，AD 为ABC ∆的中线，DE 平分BDA ∠交AB 于E ，DF 平分ADC ∠交AC 于F. 求证：EF CF BE >+例5：已知CD=AB ，∠BDA=∠BAD ，AE 是△ABD 的中线，求证：∠C=∠BAE第 14 题图DF CBEAB自检自测：1、如图，△ABC 中，BD=DC=AC,E 是DC 的中点，求证，AD 平分∠BAE 。

2、在四边形ABCD 中，AB ∥DC ，E 为BC 边的中点，∠BAE=∠EAF ，AF 与DC 的延长线相交于点F 。

试探究线段AB 与AF 、CF 之间的数量关系，并证明你的结论.3、已知：如图，在ABC ∆中，AC AB ≠，D 、E 在BC 上，且DE=EC ，过D 作BA DF //交AE 于点F ，DF=AC.求证：AE 平分BAC ∠ F EAB C DABFDEC4、如图，CB、CD分别是钝角△AEC和锐角△ABC的中线，且AC=AB．求证：①CE=2CD．②CB平分∠DCE．5、如图已知△ABC，AD是BC边上的中线，分别以AB边、AC边为直角边各向形外作等腰直角三角形，求证EF＝2AD.4、已知：如图，∆ABC 中，∠C=90︒，CM ⊥AB 于M ，AT 平分∠BAC 交CM 于D ，交BC 于T ，过D 作DE//AB 交BC 于E ，求证：CT=BE.倍长中线法（加倍法）知识网络详解：中线是三角形中的重要线段之一，在利用中线解决几何问题时，常常采用“倍长中线法”添加辅助线．所谓倍长中线法，就是将三角形的中线延长一倍，以便构造出全等三角形，从而运用全等三角形的有关知识来解决问题的方法．倍长中线法的过程：延长某某到某点，使某某等于某某，使什么等于什么（延长的那一条），用SAS 证全等（对顶角）倍长中线最重要的一点，延长中线一倍，完成SAS 全等三角形模型的构造。