倍长中线法(加倍法)

中考数学几何添加辅助线：倍长中线中线或中点是三角形中的重要线段之一，在利用中线解决几何问题时，常常采用“倍长中线法”添加辅助线。

所谓倍长中线法，就是将三角形的中线延长一倍，以便构造出全等三角形，从而运用全等三角形的有关知识来解决问题的方法。

此法常用于构造全等三角形，利用中线的性质、辅助线、对顶角进而用“SAS”证明对应边之间的关系。

常规的倍长中线可以出全等，但需要证明“三点共线”，遇到“中点+平行”，我们“延长出全等”，而非“倍长出全等”. 用“倍长中线法”作辅助线解几何题，是一种重要的技巧套路。

它可以有效地生发出全等、平行等基本条件，关联好多基本图形，帮助解题，大家务必好好掌握。

也给我们解题的启示：抓住核心，找到关键，才能快速解题。

逢中点，便倍长，全等观，平行现.倍长中线法:是指加倍延长中线，使所延长部分与中线相等，然后连接相应的顶点，构造“8字形”的全等三角形。

在与中点有关的线段尤其是涉及线段的等量关系时，倍长中线应用较常见，常见添加如图（AD是底边中线）典例1．已知：AD是ΔABC的中线，AE=EF．求证：AC=BF．名师指点：延长AD到M，使AD＝DM，连接BM，根据SAS证△ADC≌△MDB，推出BM＝AC，∠CAD＝∠M，根据AE＝EF，推出∠CAD＝∠AFE＝∠BFD，求出∠BFD＝∠M，再根据等腰三角形的性质证明即可．满分解答：证明：延长AD 到M ，使AD ＝DM ，连接BM ，∵AD 是△ABC 中线，∴CD ＝BD ，∵在△ADC 和△MDB 中，{CD ＝BD∠ADC ＝∠MDB AD ＝DM，∴△ADC ≌△MDB （SAS ），∴BM ＝AC ，∠CAD ＝∠M ，∵AE ＝EF ，∴∠CAD ＝∠AFE ，∵∠AFE ＝∠BFD ，∴∠BFD ＝∠CAD ＝∠M ，∴BF ＝BM ＝AC ，即AC ＝BF ．名师点评：倍长中线是常见的辅助线、全等中相关的角、线段的代换是解决问题的关键． 1．如图，在平行四边形ABCD 中，28CD AD ==，E 为AD 上一点，F 为DC 的中点，则下列结论中正确的是（ ）A ．4BF =B ．2ABC ABF ∠>∠。

倍长中线法知识网络详解：中线是三角形中的重要线段之一，在利用中线解决几何问题时，常常采用“倍长中线法”添加辅助线．所谓倍长中线法，就是将三角形的中线延长一倍，以便构造出全等三角形，从而运用全等三角形的有关知识来解决问题的方法．倍长中线法的过程：延长某某到某点，使某某等于某某，使什么等于什么（延长的那一条），用SAS证全等（对顶角）倍长中线最重要的一点，延长中线一倍，完成SAS全等三角形模型的构造。

经典例题讲解：例1：△ABC中，AB=5，AC=3，求中线AD的取值范围。

例2：已知在△ABC中，AB=AC，D在AB上，E在AC的延长线上，DE交BC于F，且DF=EF，求证：BD=CE例3：已知在△ABC 中，AD 是BC 边上的中线，E 是AD 上一点，且BE=AC ，延长BE 交AC 于F ，求证：AF=EF例4：如图，AD 为ABC ∆的中线，DE 平分BDA ∠交AB 于E ，DF 平分ADC ∠交AC 于F. 求证：EF CF BE >+例5：已知CD=AB ，∠BDA=∠BAD ，AE 是△ABD 的中线，求证：∠C=∠BAE例6：如图已知△ABC ，AD 是BC 边上的中线，分别以AB 边、AC 边为直角边各向形外作等腰直角三角形，求证EF ＝2AD.E D AB C第 14 题图D F C BE AF E A B C自检自测：1、如图，△ABC中，BD=DC=AC,E是DC的中点，求证，AD平分∠BAE。

2、在四边形ABCD中，AB∥DC，E为BC边的中点，∠BAE=∠EAF，AF与DC的延长线相交于点F。

试探究线段AB与AF、CF之间的数量关系，并证明你的结论.3、已知：如图，在ABC∆中，ACAB≠，D、E在BC上，且DE=EC，过D作BADF//交AE于点F，DF=AC.求证：AE平分BAC∠4、如图，CB、CD分别是钝角△AEC和锐角△ABC的中线，且AC=AB．求证：①CE=2CD．②CB平分∠DCE．FEAB CDABFD E C。

全等三角形的构造方法---常用辅助线搞清了全等三角形的证题思路后，还要注意一些较难的一些证明问题，只要构造合适的全等三角形，把条件相对集中起来，再进行等量代换，就可以化难为易了．下面举例说明几种常见的构造方法，供同学们参考．(一)倍长中线法:题中条件若有中线，可延长一倍，以构造全等三角形，从而将分散条件集中在一个三角形内。

例1．如图（1）AD 是△ABC 的中线，BE 交AC 于E ，交AD 于F ，且AE=EF ． 求证：AC=BF 证明：延长AD 至H 使DH=AD ，连BH ，∵BD=CD， ∠BDH=∠ADC ，DH=DA ， ∴△BDH ≌△CDA ，∴BH=CA ，∠H=∠DAC ，又∵AE=EF ， ∴∠DAC=∠AFE ，∵∠AFE=∠BFD ，∴∠AFE= 图（1） ∠BFD=∠DAC=∠H ，∴BF=BH ，∴AC=BF ．小结：涉及三角形中线问题时，常采用延长中线一倍的办法，即倍长中线法。

它可以将分居中线两旁的两条边AB 、AC 和两个角∠BAD 和∠CAD 集中于同一个三角形中，以利于问题的获解。

中线一倍辅助线作法△ABC 中 延长AD 到E ，AD 是BC 边中线DE=AD ，连⊥AD 于F ，延长MD AD 的延长线于使DN=MD ， 连接例2、△ABC 中，AB=5，AC=3，求中线AD 的取值范围E AB C DF H例3、已知在△ABC 中，AB=AC ，D 在AB 上，E 在AC 的延长线上，DE 交BC 于F ，且DF=EF ，求证：BD=CE课堂练习：已知在△ABC 中，AD 是BC 边上的中线，E 是AD 上一点，且BE=AC ，延长BE 交AC 于F ，求证：AF=EF例4、已知：如图，在ABC ∆中，AC AB ≠，D 、E 在BC 上，且DE=EC ，过D 作BA DF //交AE 于点F ，DF=AC.求证：AE 平分BAC ∠课堂练习：已知CD=AB ，∠BDA=∠BAD ，AE 是△ABD 的中线，求证：∠C=∠BAEB第 1 题图 A B F D EC作业：1、在四边形ABCD 中，AB ∥DC ，E 为BC 边的中点，∠BAE=∠EAF ，AF 与DC 的延长线相交于点F 。

倍长中线法(经典例题)2倍长中线法（加倍法）知识网络详解：中线是三角形中的重要线段之一，在利用中线解决几何问题时，常常采用“倍长中线法”添加辅助线．所谓倍长中线法，就是将三角形的中线延长一倍，以便构造出全等三角形，从而运用全等三角形的有关知识来解决问题的方法．倍长中线法的过程：延长某某到某点，使某某等于某某，使什么等于什么（延长的那一条），用SAS证全等（对顶角）倍长中线最重要的一点，延长中线一倍，完成SAS全等三角形模型的构造。

经典例题讲解：例1：△ABC中，AB=5，AC=3，求中线AD例2：已知在△ABC中，AB=AC，D在AB上，E在AC的延长线上，DE交BC于F，且DF=EF，求证：BD=CE例3：已知在△ABC 中，AD 是BC 边上的中线，E 是AD 上一点，且BE=AC ，延长BE 交AC 于F ，求证：AF=EF例4：如图，AD 为ABC ∆的中线，DE 平分BDA ∠交AB 于E ，DF 平分ADC ∠交AC 于F.求证：EF CF BE >+第 14 题图DF CBEAB例5：已知CD=AB ，∠BDA=∠BAD ，AE 是△ABD 的中线，求证：∠C=∠BAE自检自测：1、如图，△ABC 中，BD=DC=AC,E 是DC 的中点，求证，AD 平分∠BAE 。

2、在四边形ABCD 中，AB ∥DC ，E 为BC 边的中点，∠BAE=∠EAF ，AF 与DC 的延长线相交于点F 。

试探究线段AB 与AF 、CF 之间的数量关系，并证明你的结论.E DABCF EABCD3、已知：如图，在ABC∆中，ACAB≠，D、E在BC上，且DE=EC，过D作BADF//交AE于点F，DF=AC.求证：AE平分BAC∠4、如图，CB、CD分别是钝角△AEC和锐角△ABC的中线，且AC=AB．求证：①CE=2CD．②CB平分∠DCE．ABFD E C5、如图已知△ABC ，AD 是BC 边上的中线，分别以AB 边、AC 边为直角边各向形外作等腰直角三角形，求证EF ＝2AD.4、已知：如图，∆ABC 中，∠C=90︒，CM ⊥AB 于M ，AT 平分∠BAC 交CM 于D ，交BC 于T ，过D 作DE//AB 交BC 于E ，求证：CT=BE.DA BCMTE倍长中线法（加倍法）知识网络详解：中线是三角形中的重要线段之一，在利用中线解决几何问题时，常常采用“倍长中线法”添加辅助线．所谓倍长中线法，就是将三角形的中线延长一倍，以便构造出全等三角形，从而运用全等三角形的有关知识来解决问题的方法．倍长中线法的过程：延长某某到某点，使某某等于某某，使什么等于什么（延长的那一条），用SAS证全等（对顶角）倍长中线最重要的一点，延长中线一倍，完成SAS全等三角形模型的构造。

倍长中线法总结1. 引言倍长中线法（The Doubling Midline Method）是一种用来解决数学问题的方法，它主要应用于图形和数列的问题。

该方法通过找出中线并将其倍增来寻找问题的解。

本文将详细介绍倍长中线法的思想和应用，并通过示例展示其实际运用。

2. 思想和原理倍长中线法的思想源于对图形和数列的观察和分析。

当遇到需要找到图形或数列的某个特定点或者结果时，我们可以通过找出中线并将其倍增来逐步逼近目标。

该方法的原理是基于中线的特性，即中线两侧长度相等。

通过不断倍增中线的长度，我们可以逐步逼近目标点或结果。

3. 应用步骤倍长中线法的应用可以分为以下几个步骤：步骤一：观察问题首先，我们需要观察和分析问题，确定需要找到的目标点或结果。

这可以帮助我们确定使用倍长中线法的运算方式和步骤。

步骤二：确定初始中线然后，我们需要确定初始中线。

中线的选择要尽可能接近目标点或结果，以提高计算的准确性和效率。

步骤三：倍增中线长度接下来，我们将中线的长度倍增。

具体的倍增倍数可以根据实际情况而定。

每次倍增后，我们检查新的中线是否更接近目标点或结果。

如果是，我们继续倍增中线的长度，直到达到预定的精度要求。

步骤四：确定最终结果最后，我们确定最终结果。

根据具体的问题，我们可以根据中线的位置和长度计算出目标点的坐标或者得出数列的结果。

4. 实际应用示例为了更好地理解倍长中线法的应用，以下是一个实际示例：问题描述在平面直角坐标系中，有一条直线L通过点A(2, 3)和点B(5, 9)。

现在需要确定直线L和Y轴的交点C的坐标。

解决步骤1.观察问题，确定需要找到交点C的坐标。

2.初始中线的选择可以是线段AB的中点M，即M(3.5, 6)。

3.根据倍长中线法，将线段AM的长度倍增，得到线段CM。

4.假设线段CM的长度为d，当d接近垂直距离MC时，我们可以认为目标点C的坐标已经确定。

5.通过不断倍增线段AM的长度，我们最终确定了线段CM的长度为2.5，即MC的长度为2.5。

初中数学倍长中线法
在初中数学中，倍长中线法是一种求解三角形面积的方法。

它基于中线的性质：连接三角形两边中点的线段叫做中线，且中线的长度等于这两边之和的一半。

因此，对于任意三角形ABC，可以先求出它的三条中线长度，分别记为m_a、m_b、m_c。

然后，用海龙公式：
s = √[s(s-a)(s-b)(s-c)]
其中，s 是三角形的半周长，a、b、c是三边长度。

而半周长 s 可以用三条中线的长度求出：
s = 1/2(m_a + m_b + m_c) 这样，就可以用倍长中线法求出任意三角形的面积了。

需要注意的是，倍长中线法只适用于求解面积，不能用来求解三角形的其他属性。

但在一些实际问题中，求解面积就足够了。

- 1 -。

倍长中线法
知识网络详解：
中线是三角形中的重要线段之一，在利用中线解决几何问题时，常常采用“倍长中线法”添加辅助线．
所谓倍长中线法，就是将三角形的中线延长一倍，以便构造出全等三角形，从而运用全等三角形的有关知识来解决问题的方法．
倍长中线法的过程：延长某某到某点，使某某等于某某，使什么等于什么（延长的那一条），用SAS证全等（对顶角）
倍长中线最重要的一点，延长中线一倍，完成SAS全等三角形模型的构造。

【方法精讲】常用辅助线添加方法——倍长中线
经典例题讲解：
例1：△ABC中，AB=5，AC=3，求中线AD的取值范围
例2：已知在△ABC中，AB=AC，D在AB上，E在AC的延长线上，DE交BC于F，且DF=EF，求证：BD=CE
例3：已知在△ABC中，AD是BC边上的中线，E是AD上一点，且BE=AC，延长BE交AC 于F，求证：AF=EF
例4：已知：如图，在ABC 中，ACAB ，D、E在BC上，且DE=EC，过D作BADF//交AE 于点F，DF=AC.
求证：AE平分∠BAC
例5：已知CD=AB，∠BDA=∠BAD，AE是△ABD的中线，求证：∠C=∠BAE
、如图，△ABC中，BD=DC=AC,E是DC的中点，求证，AD平分∠BAE
在四边形ABCD中，AB∥DC，E为BC边的中点，∠BAE=∠EAF，AF与DC的延长线相交于点F。

试探究线段AB与AF、CF之间的数量关系，并证明你的结论
.。

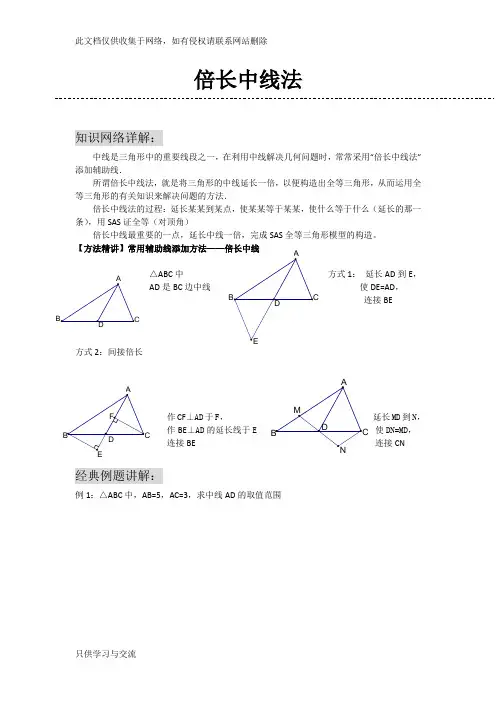
倍长中线法知识网络详解：中线是三角形中的重要线段之一，在利用中线解决几何问题时，常常采用“倍长中线法”添加辅助线．所谓倍长中线法，就是将三角形的中线延长一倍，以便构造出全等三角形，从而运用全等三角形的有关知识来解决问题的方法．倍长中线法的过程：延长某某到某点，使某某等于某某，使什么等于什么（延长的那一条），用SAS 证全等（对顶角）倍长中线最重要的一点，延长中线一倍，完成SAS 全等三角形模型的构造。

【方法精讲】常用辅助线添加方法——倍长中线△ABC 中 方式1： 延长AD 到E ，AD 是BC 边中线 使DE=AD ，连接BE方式2：间接倍长作CF ⊥AD 于F ， 延长MD 到N ，作BE ⊥AD 的延长线于E 使DN=MD ， 连接BE 连接CN经典例题讲解：例1：△ABC 中，AB=5，AC=3，求中线AD 的取值范围D ABCEDAB C F EDC B AN D C B AM例2：已知在△ABC 中，AB=AC ，D 在AB 上，E 在AC 的延长线上，DE 交BC 于F ，且DF=EF ，求证：BD=CE过D 作DG//AC例3：已知在△ABC 中，AD 是BC 边上的中线，E 是AD 上一点，且BE=AC ，延长BE 交AC 于F ，求证：AF=EF例4：已知：如图，在ABC ∆中，AC AB ≠，D 、E 在BC 上，且DE=EC ，过D 作BA DF //交AE 于点F ，DF=AC. 求证：AE 平分BAC ∠FE DA B CF EC ABD ABFDEC例5：已知CD=AB ，∠BDA=∠BAD ，AE 是△ABD 的中线，求证：∠C=∠BAE自检自测：1、如图，△ABC 中，BD=DC=AC,E 是DC 的中点，求证，AD 平分∠BAE.2、在四边形ABCD 中，AB ∥DC ，E 为BC 边的中点，∠BAE=∠EAF ，AF 与DC 的延长线相交于点F 。

试探究线段AB 与AF 、CF 之间的数量关系，并证明你的结论.E D ABCF EAB C D3、如图，AD 为ABC ∆的中线，DE 平分BDA ∠交AB 于E ，DF 平分ADC ∠交AC 于F. 求证：EF CF BE >+4、已知：如图，∆ABC 中，∠C=90︒，CM ⊥AB 于M ，AT 平分∠BAC 交CM 于D ，交BC 于T ，过D 作DE//AB 交BC 于E ，求证：CT=BE.第 14 题图DF CBEADABCMTE。

全等模型—倍长中线模型知识点管理归类探究夯实双基，稳中求进倍长中线模型三角形的中线：三角形的顶点和对边中点的连线三角形边长的不等关系：在三角形中，两边之和大于第三边，两边只差小于第三边倍长中线定义：“倍长中线”是指加倍延长中线，使所延长部分与中线相等，然后往往需要连接相应的顶点，则对应角对应边都对应相等。

常用于构造全等三角形。

中线倍长法多用于构造全等三角形和证明边之间的关系（通常用“SAS ”证明）（注：一般都是原题已经有中线时用，不太会有自己画中线的时候）。

题型一：求三角形中线取值范围【例1】（2021·重庆市暨华中学校八年级月考）在ABC 中，5AC =，中线7AD =，则AB 边的取值范围（）A ．212AB <<B ．412AB <<C ．919AB <<D ．1019AB <<【答案】C 【分析】延长AD 至E ，使DE =AD ，然后利用“边角边”证明△ABD 和△ECD 全等，根据全等三角形对应边相等可得AB =CE ，再利用三角形的任意两边之和大于第三边，三角形的任意两边之差小于第三边求出CE 的取值范围，即为AB 的取值范围．【详解】解：如图，延长AD 至E ，使DE =AD ，∵AD 是△ABC 的中线，∴BD =CD ，在△ABD 和△ECD 中，BD CD ADB EDC AD DE ⎪∠⎪⎩∠⎧⎨＝＝＝，∴△ABD ≌△ECD （SAS ），∴AB =CE ，∵AD =7，∴AE =7+7=14，∵14+5=19，14-5=9，∴9＜CE ＜19，即9＜AB ＜19．故选：C ．【点睛】本题考查了全等三角形的判定与性质，三角形的任意两边之和大于第三边，三角形的任意两边之差小于第三边，“遇中线，加倍延”构造出全等三角形是解题的关键．变式训练【变式1-1】（2021·全国）如图，AD 是ABC 的边BC 上的中线，7,5AB AD ==，则AC 的取值范围为（）A ．515AC <<B ．315AC <<C ．317AC <<D ．517AC <<【答案】C 【分析】延长AD 至点E ，使5DE AD ==，连接CE ，证明ABD ECD ≌，可得7CE AB ==，然后运用三角形三边关系可得结果．【详解】如图，延长AD 至点E ，使5DE AD ==，连接CE．∵AD 为ABC 的BC 边上的中线，∴BD CD =，在ABD △和ECD 中，,,,AD ED ADB EDC BD CD =⎧⎪∠=∠⎨⎪=⎩∴()SAS ABD ECD ≌，∴7CE AB ==．在ACE 中，AE EC AC AE CE -<<+，即557557AC +-<<++，∴317AC <<，故选：C ．【点睛】本题考查了全等三角形的判定与性质，三角形三边关系，根据中点倍长法构造全等三角形是解题的关键．【变式1-2】（2021·武汉一初慧泉中学八年级月考）已知AD 是△ABC 的中线，AD =6，CA =5，则边AB 的取值范围是______．【答案】7<AB <17【分析】作出图形，延长AD 至E ，使DE =AD ，然后利用“边角边”证明△ABD 和△ECD 全等，根据全等三角形对应边相等可得AB =CE ，再利用三角形的任意两边之和大于第三边，三角形的任意两边之差小于第三边求出CE 的取值范围，即为AB 的取值范围．【详解】解：如图，延长AD 至E ，使DE =AD，∵AD 是△ABC 的中线，∴BD =CD ，在△ABD 和△ECD 中，BD CD ADB EDC AD DE ⎧⎪∠∠⎨⎪⎩＝＝＝，∴△ABD ≌△ECD （SAS ），∴AB =CE ，∵AD =6，∴AE =6+6=12，∵12+5=17，12-5=7，∴7＜CE ＜17，即7＜AB ＜17．故答案为：7＜AB ＜17．【点睛】本题考查了全等三角形的判定与性质，三角形的任意两边之和大于第三边，三角形的任意两边之差小于第三边，“遇中线，加倍延”构造出全等三角形是解题的关键．【变式1-3】（2021·全国）△ABC 中，AB =8，AC =6，AD 是BC 边上的中线，则AD 长度的范围是__________．【答案】1＜AD ＜7【分析】延长AD 至E ，使DE =AD ，连接CE ．根据SAS 证明△ABD ≌△ECD ，得CE =AB ，再根据三角形的三边关系即可求解．【详解】解：延长AD 至E ，使DE =AD ，连接CE．在△ABD 和△ECD 中，DE AD ADB CDE DB DC =⎧⎪∠=∠⎨⎪=⎩，∴△ABD ≌△ECD （SAS ），∴CE =AB ．在△ACE 中，CE -AC ＜AE ＜CE +AC ，即2＜2AD ＜14，故1＜AD ＜7．故答数为：1＜AD ＜7．【点睛】本题主要考查了全等三角形的判定和性质、三角形的三边关系．注意：倍长中线是常见的辅助线之一．【变式1-4】（2021·陕西城固·七年级期末）如图，在ABC 中，AD 是BC 边上的中线，过C 作AB 的平行线交AD 的延长线于E 点．若6AB =，2AC =，试求AE的取值范围．【答案】4＜AE ＜8【分析】证明△ABD ≌△ECD （AAS ），得到AB =EC =6，AD =ED ，再由三角形的三边关系即可得出答案．【详解】解：∵AD 是BC 边上的中线，∴BD =C D ．∵AB ∥CE ，∴∠BAD =∠E ，在△ABD 和△ECD 中，BAD E BDA CDE BD CD ∠=∠⎧⎪∠=∠⎨⎪=⎩，∴△ABD ≌△ECD （AAS ），∴AB =EC =6，∴AD =DE ，在△ACE 中，CE -AC ＜AE ＜CE +AC ，即6-2＜AE ＜6+2，∴4＜AE ＜8．【点睛】本题考查了全等三角形的判定与性质、平行线的性质、三角形的三边关系等知识；熟练掌握三角形的三边关系，证明三角形全等是解题的关键．题型二：利用倍长中线证明线段、角相等【例题2】（2021·全国八年级课时练习）如图，CE 、CB 分别是ABC 与ADC 的中线，且∠=∠ACB ABC ，AC AB =．求证：2CD CE =．【答案】见解析【详解】解析：过点B 作//BF AC 交CE 的延长线于点F ，由点E 为AB 中点，得到AE EB =，再由BF 与AC 平行，得到两对内错角相等，利用AAS 得到ACE 与BFE △全等，利用全等三角形的对应边相等得到CE EF =，AC BF =，即2CF CE =，再由AC AB =，根据点B 为AD 中点，得到AC AB BD BF ===，利用外角性质及等量代换得到DBC FBC ∠=∠，利用SAS 得到CBD 与CBF V 全等，利用全等三角形对应边相等得到CD CF =，等量代换即可得证．答案：证明：如图，过点B 作//BF AC 交CE 的延长线于点F．∵CE 是ABC 的中线，//BF AC ，∴AE BE =，A ABF ∠=∠，ACE F ∠=∠，在ACE 和BFE △中，∵,,,A ABF ACE F AE BE ∠=∠⎧⎪∠=∠⎨⎪=⎩∴ACE BFE ≌（AAS ），∴CE EF =，AC BF =，∴2CF CE =，又∵AC AB =，CB 是ADC 的中线，∴AC AB BD BF ===，∵DBC A ACB ABF ABC ∠=∠+∠=∠+∠，∵∠=∠ACB ABC ，∴DBC FBC ∠=∠，在DBC △和FBC 中，∵,,,DB FB DBC FBC BC BC =⎧⎪∠=∠⎨⎪=⎩∴DBC FBC ≌（SAS ），∴2DC CF CE ==．易错：证明：在ACE 和BFE △中，,,,A ABF AE BE ACE F ∠=∠⎧⎪=⎨⎪∠=∠⎩∴ACE BFE ≌（ASA ）．错因：写错证明方法．满分备考：遇到三角形的中线，可通过倍长中线，使延长线段与原中线长相等，构造全等三角形解决问题．变式训练【变式2-1】（2019·呼和浩特市实验中学八年级期中）（1）AD 是ABC ∆的中线，8AB =，6AC =则AD 的取值范围是__________．（2）在（1）问的启发下，解决下列问题：如图，AD 是ABC ∆的中线，BE 交AC 于E ，交AD 于F ，且AE EF =，求证：AC BF =．【答案】（1）17AD <<（2）见解析【分析】（1）根据倍长中线法将AD 延长一倍，再证△ADC ≌△GDB ，根据三角形的三边关系即可求出AG 的取值范围，从而求出AD 的取值范围；（2）由（1）中结论：△ADC ≌△GDB ，即可得到：AC=BG ，∠CAD=∠G ，再根据等腰三角形的性质和判定即可得到BG=BF=AC.【详解】（1）将AD 延长至G ，使AD=DG ，连接BG，如下图所示：在△ADC 和△GDB 中CD BD ADC GDB AD DG =⎧⎪∠=∠⎨⎪=⎩∴△ADC ≌△GDB∴AC=BG=6在△ABG 中AB BG AG AB BG-<<+∴86286AD -<<+∴17AD <<（2）将AD 延长至G ，使AD=DG ，连接BG，如下图所示：由（1）中结论：△ADC ≌△GDB∴AC=BG ，∠CAD=∠G又∵AE EF =，∴AFE EAF ∠=∠，∴AFE G∠=∠∵AFE BFG∠=∠∴G BFG∠=∠∴BG=BF=AC【点睛】此题考查的是全等三角形的判定及等腰三角形的判定及性质，掌握用倍长中线法构造全等三角形是解决此题的关键.【变式2-2】（2020·湖南长沙市·月考）如图，已知在ABC ∆中，AD 是BC 边上的中线，E 是AD 上一点，且BE AC =，延长BE 交AC 于F ，求证：AF EF =、【分析】利用中线类倍长的基本模型进行证明，结合等腰三角形的性质进行论证．【详解】延长AD 到G ，使DG AD =，连结BG∵BD CD =，BDG CDA ∠=∠，AD GD=∴ADC GDB ∆∆≌．∴AC GB =．G EAF∠=∠又∵BE AC =，∴BE BG=∴G BED ∠=∠，而BED AEF∠=∠∴AEF FAE ∠=∠，故FA FE =．【点睛】此题考查的是全等三角形的判定及等腰三角形的判定及性质，掌握用倍长中线法构造全等三角形是解决此题的关键.【变式1-3】（2021·陕西碑林·交大附中分校七年级期中）问题背景：课外兴趣小组活动时，老师提出了如下问题：如图1，△ABC 中，若AB ＝4，AC ＝3，求BC 边上的中线AD 的取值范围．小明在组内经过合作交流，得到了如下的解决方法：延长AD 到点E ，使DE ＝AD ，则得到△ADC ≌△EDB ，小明证明△BED ≌△CAD 用到的判定定理是：（用字母表示）；问题解决：小明发现：解题时，条件中若出现“中点”“中线”字样，可以考虑延长中线构造全等三角形，把分散的已知条件和所求证的结论集合到同一个三角形中．请写出小明解决问题的完整过程；拓展应用：以△ABC 的边AB ，AC 为边向外作△ABE 和△ACD ，AB ＝AE ，AC ＝AD ，∠BAE ＝∠CAD ＝90°，M 是BC 中点，连接AM ，DE ．当AM ＝3时，求DE 的长．【答案】问题背景：SAS ；问题解决：完整过程见解析；拓展应用：DE ＝6．【分析】问题背景：先判断出BD =CD ，由对顶角相等∠BDE =∠CDA ，进而得出△ADC ≌△EDB （SAS ）；问题解决：先证明△ADC ≌△EDB （SAS ），得出BE =AC =3，最后用三角形三边关系即可得出结论；拓展应用：如图2，延长AM 到N ，使得MN =AM ，连接BN ，同（1）的方法得出△BMN ≌△CMA （SAS ），则BN =AC ，进而判断出∠ABN =∠EAD ，进而判断出△ABN ≌△EAD ，得出AN =ED ，即可求解．【详解】问题背景：如图1，延长AD 到点E ，使DE ＝AD ，连接BE，∵AD 是△ABC 的中线，∴BD ＝CD ，在△ADC 和△EDB 中，AD ED CDA BDE CD BD =⎧⎪∠=∠⎨⎪=⎩，∴△ADC ≌△EDB （SAS ），故答案为：SAS ；问题解决：如图1，延长AD 到点E ，使DE ＝AD ，连接BE ，∵AD 是△ABC 的中线，∴BD ＝CD ，在△ADC ≌△EDB 中，AD ED CDA BDE CD BD =⎧⎪∠=∠⎨⎪=⎩，∴△ADC ≌△EDB （SAS ），∴BE ＝AC ，在△ABE 中，AB ﹣BE ＜AE ＜AB +BE ，∵AB ＝4，AC ＝3，∴4﹣3＜AE ＜4+3，即1＜AE ＜7，∵DE ＝AD ，∴AD ＝12AE ，∴12＜AD ＜72；拓展应用：如图2，延长AM 到N ，使得MN ＝AM ，连接BN，由问题背景知，△BMN ≌△CMA （SAS ），∴BN ＝AC ，∠CAM ＝∠BNM ，∴AC //BN ，∵AC ＝AD ，∴BN ＝AD ，∵AC //BN ，∴∠BAC +∠ABN ＝180°，∵∠BAE ＝∠CAD ＝90°，∴∠BAC +∠EAD ＝180°，∴∠ABN ＝∠EAD ，在△ABN 和△EAD 中，AB EA ABN EAD BN AD =⎧⎪∠=∠⎨⎪=⎩，∴△ABN ≌△EAD （SAS ），∴AN ＝DE ，∵MN ＝AM ，∴DE ＝AN ＝2AM ，∵AM ＝3，∴DE ＝6．【点睛】此题考查了全等三角形的判定和性质，平行线的判定与性质，补角的性质，掌握倍长中线法，构造全等三角形是解本题的关键．类倍长中线模型【例题3】（2020·宜春市宜阳学校八年级月考）阅读理解：（1）如图1，在ABC 中，若10AB =，6AC =，求BC 边上的中线AD 的取值范围．解决此问题可以用如下方法：延长AD 到点E ，使得AD DE =，再连接BE ，把AB ，AC ，2AD 集中在ABE △中，利用三角形三边关系即可判断中线AD 的取值范围是______．（2）解决问题：如图2，在ABC 中，D 是BC 边上的中点，DE DF ⊥，DE 交AB 于点E ，DF 交AC 于点F ，连接EF ，求证：BE CF EF +>．【答案】（1）28AD <<；（2）见解析；【分析】（1）如图1延长AD 到点E ，使得AD DE =，再连接BE ，由AD 为中线，推出BD=CD ，可证△ACD ≌△EBD （SAS ）得AC=EB ，在ABE △中，由三边关系4<2AD<16即可，（2）如图2延长FD 到G ，使DG=FD ，连结BG ，EG 由D 为BC 中点，BD=CD 可证△FCD ≌△GBD （SAS ）得FC=GB ，由DE DF ⊥，DF=DG 得EF=EG ，在△BEG 中由三边关系，【详解】（1）如图1延长AD 到点E ，使得AD DE =，再连接BE ，∵AD 为中线，∴BD=CD ，在△ADC 和△EDB 中，∵CD=BD ，∠ADC=∠EDB ，AD=ED ，∴△ACD ≌△EBD （SAS ），∴AC=EB=6，ABE △，∵AB-BE<AE<AB+BE ，∴4<2AD<16，∴2<AD<8，（2）如图2延长FD 到G ，使DG=FD ，连结BG ，EG ，由D 为BC 中点，BD=CD ，在△FDC 和△GDB 中，∵CD=BD ，∠FDC=∠GDB ，FD=GD ，∴△FCD ≌△GBD （SAS ），∴FC=GB ，∵DE DF ⊥，DF=DG ，∴EF=EG ，在△BEG 中EG<EB+BG ，即BE CF EF +>，【点睛】本题考查中线加倍，三角形全等，三边关系，垂直平分线，等腰三角形，掌握中线加倍构造三角形，用三角形全等转化等量关系，用三边关系求取值范围，用垂直平分线转化线段，用等腰三角形证角是解题关键，变式训练【变式3-1】（2021·广东广州市·月考）如图，在ABC ∆中，AD 交BC 于点D ，点E 是BC 中点，EF AD ∥交CA 的延长线于点F ，交AB 于点G ，若BG CF =，求证：AD 为ABC ∆的角平分线．【分析】通过补长EG ，转换成倍长中线模型【详解】延长FE 到点H ，使得EF EH =，连结BH∵E 是BC 的中点∴BE CE=在EFC ∆和EHB ∆中，CE BE CEF BEHEF EH =⎧⎪∠=∠⎨⎪=⎩∴EFC ∆≌EHB∆∴FC BH =，F H∠=∠∵BG CF=∴BH BG=∴H BGH∠=∠∴F BGH∠=∠∵EF AD∥∴,F CAD BGH BAD∠=∠∠=∠∴CAD BAD∠=∠∴AD 为ABC ∆的角平分线.【变式3-2】（2021·湖北随州市·八年级期末）在通过构造全等三角形解决的问题中，有一种典型的方法是倍延中线．如图3，在四边形ABCD 中，//AD BC ，点E 是AB 的中点，连接CE ，ED 且CE DE ⊥，试猜想线段,,BC CD AD 之间满足的数量关系，并予以证明．【分析】延长CE 到F ，使EF EC =，连接AF ，即可证明AEF BEC ∆≅∆，则可得EAF B AF BC ∠=∠=，，由//AD BC ，以及角度关系即可证明点,,F A D 在一条直线上，通过证明Rt DEF △≌DEC Rt △，即可得到FD CD =，进而通过线段的和差关系得到CD BC AD =+．【详解】（3）CD BC AD =+，延长CE 到F ，使EF EC =，连接AF，AE BE AEF BEC =∠=∠ ，，AEF BEC ∴∆≅∆，EAF B AF BC ∴∠=∠=，，//AD BC ，180BAD B ∴∠+∠=︒，180EAF BAD ∴∠+∠=︒，∴点,,F A D 在一条直线上，CE ED ⊥ ，∴90DEF DEC ==︒∠∠，∴在Rt DEF △和DEC Rt △中，EF EC =，DEF DEC ∠=∠，DE DE =，∴Rt DEF △≌DEC Rt △，FD CD ∴=，∵FD AD AF AD BC =+=+，CD BC AD ∴=+．【点睛】本题考查了三角形中线、全等三角形的证明和性质、三角形的三边关系、等腰三角形的性质、平行线的性质、平角的概念、线段的和差关系等，正确的作出辅助线以及综合运用以上知识是解答本题的关键．【变式3-3】（江苏省南京玄武外国语学校、十三中科利华集团校2019-2020学年八年级下学期期中数学试题）课外兴趣小组活动时，老师提出了如下问题：如图1，在△ABC 中，若AB ＝5，AC ＝3，求BC 边上的中线AD 的取值范围．小明在组内经过合作交流，得到了如下的解决方法：延长AD 到E ，使得DE ＝AD ，再连接BE （或将△ACD 绕点D 逆时针旋转180°得到△EBD ），把AB 、AC 、2AD 集中在△ABE 中，利用三角形的三边关系可得2＜AE ＜8，则1＜AD ＜4．（感悟）解题时，条件中若出现中点、中线字样，可以考虑构造以中点为对称中心的中心对称图形，把分散的已知条件和所求证的结论集中到同一个三角形中．（解决问题）受到（1）的启发，请你证明下列命题：如图2，在△ABC 中，D 是BC 边上的中点，DE ⊥DF ，DE 交AB 于点E ，DF 交AC 于点F ，连接EF ．求证：BE ＋CF ＞EF ，【答案】（1）见解析；（2）222=BE CF EF ＋，见解析【分析】延长FD 到G ，使得DG=DF ，连接BG 、EG ．（或把△CFD 绕点D 逆时针旋转180°得到△BGD ），利用三角形的三边关系即可解决问题；【详解】解：延长FD 到G ，使得DG=DF ，连接BG 、EG ．（或把△CFD 绕点D 逆时针旋转180°得到△BGD ），∴CF=BG ，DF=DG ，∵DE ⊥DF ，∴EF=EG ．在△BEG 中，BE+BG ＞EG ，即BE+CF ＞EF ．【点睛】本题考查了旋转的性质、全等三角形的判定和性质、三角形的三边关系、三角形的面积等知识，解题的关键是学会添加常用辅助线，构造全等三角形解决问题．综合提升变式练一、填空题1．（2022·安徽亳州·八年级期末）如图，在△ABC 中，AD 为中线，6AB ．（1）若4AC =，AD 长度为a ，则a 的取值范围为________；（2）若AD AC ⊥，30BAD ∠=︒，则AC 的长度为________．【答案】15a <<3【分析】（1）延长中线AD 到E ，使DE AD =，可证△ACD ≌△EBD （SAS ），得AC BE =，根据三角形的三边关系可得64264a -<<+，求解即可；（2）延长AD ，使AD DF =，连接CF ，可证△ABD ≌△FCD （SAS ），得BAD CFD ∠=∠，AB FC =，在Rt △AFC 中，根据30°所对的直角边等于斜边的一半可得12AC FC =，从而可求．【详解】解：（1）如图1，延长中线AD 到E ，使DE AD =，∵AD 是三角形的中线，∴BD CD =，在△ACD 和△EBD 中，CD BD ADC BDE AD DE =⎧⎪∠=∠⎨⎪=⎩，∴△ACD ≌△EBD （SAS ），∴AC BE =，∵4BE AC ==，6AB =，第三边上的中线为a ，∴64264a -<<+，即2210a <<，∴15a <<．故答案为：15a <<．（2）如图2，延长AD ，使AD DF =，连接CF，∵AD 为中线，∴BD CD =，在△ABD 和△FCD 中，AD FD ADB FDC BD CD =⎧⎪∠=∠⎨⎪=⎩，∴△ABD ≌△FCD （SAS ），∴BAD CFD ∠=∠，AB FC =，∵30BAD ∠=︒，∴30CFD ∠=︒，∵AD AC ⊥，∴90CAD ∠=︒，∴12AC FC =，∵6AB =，∴132AC AB ==．【点睛】本题考查了延长中线构成全等三角形，及全等三角形的判定与性质，直角三角形的性质，解题的关键是延长中线作辅助线构造全等三角形．2．（2021·江苏·徐州市第二十六中学八年级阶段练习）如图，AD 是△ABC 中BC 边上的中线，若AB ＝6，AC ＝8，则AD 的取值范围是________________．【答案】1＜AD ＜7【分析】延长AD 到E ，使DE =AD ，然后利用“边角边”证明△ABD 和△ECD 全等，根据全等三角形对应边相等可得CE =AB ，然后根据三角形任意两边之和大于第三边，两边之差小于第三边求出AE 的取值范围，然后即可得解．【详解】解：如图，延长AD 到E ，使DE =AD ，∵AD 是BC 边上的中线，∴BD =CD ，在△ABD 和△ECD 中,BD CD ADB EDC AD ED =⎧⎪∠=∠⎨⎪=⎩，∴△ABD≌△ECD(SAS)，∴CE=AB，∵AB=6，AC=8，∴8-6<AE<8+6，即2<2AD<14，∴1<AD<7，故答案为：1<AD<7．【点睛】本题考查了三角形的三边关系，全等三角形的判定与性质，遇中点加倍延，作辅助线构造出全等三角形是解题的关键．3．（2021·河北·廊坊市第四中学八年级阶段练习）在△ABC中，AB＝9，AC＝5，AD是△ABC 的中线，则AD的取值范围是_____．【答案】2＜AD＜7【分析】延长中线利用全等，使AD与已知两边满足三角形的三边关系．【详解】解：延长AD到E，使AD＝DE，连接BE，∵AD 是△ABC 的中线，∴BD ＝CD ，在△ADC 和△EDB 中，CD BD ADC BDE AD DE =⎧⎪∠=∠⎨⎪=⎩，∴△ADC ≌△EDB （SAS ），∴EB ＝AC ，根据三角形的三边关系定理：9﹣5＜AE ＜9+5，∴2＜AD ＜7，故答案为：2＜AD ＜7．【点睛】本题考查三角形的中线，全等三角形的判定（SAS ），三角形的三边长度关系；延长三角形的中线证明全等是常用的解题方法，要熟练掌握．二、解答题4．（2022·贵州毕节·二模）课外兴趣小组活动时，老师提出了如下问题：(1)如图1，△ABC 中，若AB =5，AC =3，求BC 边上的中线AD 的取值范围．小明在组内经过合作交流，得到了如下的解决方法：延长AD 到点E ，使DE =AD ，请根据小明的方法思考帮小明完成解答过程．(2)如图2，AD 是△ABC 的中线，BE 交AC 干E ，交AD 于F ，且AE =EF ．请判昕AC 与BF 的数量关系，并说明理由．【答案】(1)见解析(2)AC =BF ，理由见解析(1)解：如图，延长AD 到点E ，使DE =AD ，连接BE ，在△ADC 和△EDB 中∵AD DE ADC EDB CD DB =⎧⎪∠=∠⎨⎪=⎩，∴△ADC ≌△EDB （SAS ）．∴BE =AC =3．∵AB -BE <AE <AB +BE∵2<AE <8．∵AE =2AD∴1<AD <4．(2)AC =BF ，理由如下：延长AD 至点G ，使GD =AD ，连接BG，在△ADC 和△GDB 中，AD DG ADC GDB BD CD =⎧⎪∠=∠⎨⎪=⎩，∴△ADC ≌△GDB （SAS ）．∴BG =AC ，∠G =∠DAC ．．∵AE =EF∴∠AFE =∠FAE ．∴∠DAC =∠AFE =∠BFG∴∠G =∠BFG∴BG =BF∴AC =BF ．【点睛】本题考查全等三角形判定与性质，三角形三边的关系，作辅助线：延长AD 到点E ，使DE =AD ，构造全等三角形是解题的关键．5．（2022·广西贵港·九年级期末）如图，在平行四边形ABCD 中，点E 、F 分别在边BC ，CD 上，AE 与BF 相交于点O ，AE AD =，AE 平分BF ，AF 平分∠DAE ．(1)求证：OA OE BE =+；(2)求证：22BE OE AE =⋅．【答案】(1)见解析(2)见解析【分析】（1）如图1，过点F 作FP BC ∥，FP 与AE 交于点P ，先证明,,PF BE OP OE ==再证明,AP PF =从而可得结论；（2）如图2，过点F 作FP BC ∥，FP 与AE 交于点P ，连接EF ，PB ，证明BPE ABE ∠=∠，结合BEP AEB ∠=∠，证明△BEP ∽△AEB ，可得BE AE PE BE=，从而可得结论.(1)证明：如图1，过点F 作FP BC ∥，FP 与AE 交于点P ，∴FPO BEO ∠=∠，∵AE 平分BF ，即FO BO =，又FOP BOE ∠=∠，∴△POF ≌△EOB ，∴OP OE =，PF EB =，又∵四边形ABCD 是平行四边形，∴PF BC AD ∥∥，∴PFA DAF ∠=∠，∵AF 平分∠DAE ，∴PFA DAF PAF ∠=∠=∠，∴PA PF BE ==，∴OA OP PA OE BE =+=+．(2)如图2，过点F 作FP BC ∥，FP 与AE 交于点P ，连接EF ，PB ．∵AE AD =，AF 平分∠DAE ，AF AF =，∴△AEF ≌△ADF ，∴AEF D ∠=∠，又在ABCD 中，ABE D ∠=∠，又由（1）知：△POF ≌△EOB ，,,PF BE FPO BEO ∴=∠=∠,PF BE ∴ ∴四边形BEFP 是平行四边形，∴BPE AEF D ∠=∠=∠，∴BPE ABE ∠=∠，又BEP AEB ∠=∠，∴△BEP ∽△AEB ，∴BE AE PE BE=，∴2BE PE AE =⋅，又2PE OE =，∴22BE OE AE =⋅．【点睛】本题考查的是平行四边形的性质，全等三角形的判定与性质，相似三角形的判定与性质，“熟练运用以上知识，作出适当的辅助线”是解本题的关键.6．（2022·湖南长沙·八年级阶段练习）已知：如图，Rt △ABC 中，AC ＞BC ，∠ACB =90，CD 是△ABC 的中线，点E 在CD 上，且∠AED =∠B ．求证：AE =BC．【答案】见解析【分析】先通过延长CD 到F 使DF =CD ，连接AF ，构造出△BCD 的全等三角形△AFD ，由全等三角形性质可得∠F =∠BCD ，BC =AF ，又根据直角三角形斜边的中线等于斜边的一半得到CD =BD ，∠B =∠BCD ，由等量代换和等角对等边就可推出AE =BC ．【详解】证明：延长CD 到F 使DF =CD ，连接AF，如图∵CD 是△ABC 的中线，∴AD =BD ，在△ADF 与△BCD 中，AD BD ADF BDC DF DC =⎧⎪∠=∠⎨⎪=⎩，∴△ADF ≌△BDC （SAS ），∴∠F =∠BCD ，BC =AF ，∵∠ACB =90°，CD 是△ABC 的中线，∴CD =BD ，∴∠B =∠BCD ，又∵∠AED =∠B∴∠AED =∠BCD ，∵△ADF ≌△BDC ，∴∠F =∠BCD ，∴∠AED =∠F ，∴AE =AF ，∵BC =AF ，∴AE =BC ．【点睛】本题主要考查了全等三角形的性质和判定，能正确构造出全等三角形是做出本题的重点．7．（2020·海南·海口市第七中学八年级期中）某数学兴趣小组在活动时，老师提出了这样一个问题：如图，在ABC 中，AB ＝6，AC ＝8，D 是BC 的中点，求BC 边上的中线AD 的取值范围．小明在组内经过合作交流，得到了如下的解决方法：延长AD 到E ，使DE ＝AD ，请补充完整证明“△ABD ≌△ECD ”的推理过程．(1)求证：△ABD ≌△ECD证明：延长AD 到点E ，使DE ＝AD在△ABD 和△ECD 中∵AD ＝ED （已作）∠ADB ＝∠EDC （）CD ＝（中点定义）∴△ABD ≌△ECD （）(2)由（1）的结论，根据AD 与AE 之间的关系，探究得出AD 的取值范围是；(3)【感悟】解题时，条件中若出现“中点”“中线”等字样，可以考虑延长中线构造全等三角形，把分散的已知条件和所求证的结论集合到同一个三角形中．【问题解决】如下图，ABC 中，90B ∠=︒，2AB =，AD 是ABC 的中线，CE BC ⊥，4CE =，且90ADE ∠=︒，求AE 的长．【答案】(1)对顶角相等；BD ；SAS(2)17AD <<(3)6【分析】（1）延长AD 到点E ，使DE =AD ，根据SAS 定理证明△ABD ≌△ECD ；（2）根据全等三角形的性质、三角形的三边关系计算；（3）延长AD 交EC 的延长线于F ，证明△ABD ≌△FCD ，△ADE ≌△FDE ，根据全等三角形的性质解答．(1)延长AD 到点E ，使DE ＝AD在△ABD 和△ECD 中∵AD ＝ED （已作）∠ADB ＝∠EDC （对顶角相等）CD ＝BD （中点定义）∴△ABD ≌△ECD （SAS ）故答案为：对顶角相等；BD ；SAS(2)∵△ABD ≌△ECD ，AB ＝6，AC ＝8，6CE AB ∴==，8686AE -<<+，1AD 7∴<<，故答案为1AD 7<<；(3)延长AD 交EC 的延长线于F ，AB BC ⊥ ，EF BC ⊥，ABD FCD ∴∠=∠，在ABD △和FCD 中，ABD FCD BD CD ADB FDC ∠=∠⎧⎪=⎨⎪∠=∠⎩，ABD ∴ ≌FCD ，2CF AB ∴==，AD DF =，又∵∠FDE ＝∠ADE ＝90°ED ＝ED∴△ADE ≌△FDEAE EF ∴=，426EF CE CF CE AB =+=+=+= ，6AE ∴=．【点睛】本题考查了三角形的三边关系定理和全等三角形的性质和判定，解题关键是熟记全等三角形的判定条件．8．（2022·全国·一模）如图，在△ABC 中，∠ACB ＝90°，BC ＞AC ，CD ⊥AB 于点D ，点E 是AB 的中点，连接CE．(1)若AC ＝3，BC ＝4，求CD 的长；(2)求证：BC 2﹣AC 2＝2DE •AB ；(3)求证：CE ＝12AB ．【答案】(1)125(2)见解析(3)见解析【分析】（1）根据勾股定理求出AB ，根据三角形的面积公式计算，求出CD ；（2）根据题意得到BD ﹣AD ＝2DE ，根据勾股定理计算即可证明；（3）延长CE 至点F ，使EF ＝CE ，连结AF ，证明△AEF ≌△BEC （SAS ），根据全等三角形的性质得到∠B ＝∠EAF ，AF ＝BC ，再证明△ACF ≌△CAB ，得到CF ＝AB ，证明结论．(1)解：在△ABC 中，∠ACB ＝90°，AC ＝3，BC ＝4，由勾股定理得：AB5，∵∠ACB ＝90°，CD ⊥AB ，∴S △ABC ＝12AC •BC ＝12AB •DE ，即12×3×4＝12×5×CD ，解得：CD ＝125；(2)证明：∵点E 是AB 的中点，∴AE ＝BE ，∴BD ﹣AD ＝（BE +DE ）﹣（AE ﹣DE ）＝BE ﹣AE +2DE ＝2DE ，∵CD ⊥AB ，∴BC 2＝BD 2+CD 2，AC 2＝AD 2+CD 2，∴BC 2﹣AC 2＝（BD 2+CD 2）﹣（AD 2+CD 2）＝BD 2﹣AD 2＝（BD +AD ）（BD ﹣AD ）＝AB •2DE ＝2DE •AB ；(3)证明：延长CE 至点F ，使EF ＝CE ，连结AF，在△AEF 和△BEC 中，AE BE AEF BEC EF EC =⎧⎪∠=∠⎨⎪=⎩，∴△AEF ≌△BEC （SAS ），∴∠B ＝∠EAF ，AF ＝BC ，∵∠ACB ＝90°，∴∠B +∠CAB ＝∠EAF +∠CAB ＝90°，∴∠CAF ＝∠ACB ＝90°，∵AC ＝CA ，∴△ACF ≌△CAB （SAS ），∴CF ＝AB ，∵CF ＝2CE ，∴CE ＝12AB ．【点睛】本题考查的是全等三角形的判定和性质、三角形的面积计算、勾股定理的应用，掌握全等三角形的判定定理和性质定理是解题的关键．9．（2022·辽宁葫芦岛·八年级期末）已知：多项式x 2+4x +5可以写成（x ﹣1）2+a （x ﹣1）+b 的形式．(1)求a ，b 的值；(2)△ABC 的两边BC ，AC 的长分别是a ，b ，求第三边AB 上的中线CD 的取值范围．【答案】(1)6a =，10b =(2)2<CD <8【分析】（1）把()()211x a x b -+-+展开，然后根据多项式x 2+4x +5可以写成（x ﹣1）2+a（x ﹣1）+b 的形式，可得2415a a b -=⎧⎨-+=⎩，即可求解；（2）延长CD 至点H ，使CD =DH ，连接AH ，可得△CDB ≌△HAD ，从而得到BC =AH =a =6，再根据三角形的三边关系，即可求解．(1)解：∵()()211x a x b-+-+221x x ax a b =-++-+()221x a x a b =+-+-+，根据题意得：x 2+4x +5=（x ﹣1）2+a （x ﹣1）+b∴2415a a b -=⎧⎨-+=⎩，解得：610a b =⎧⎨=⎩；(2)解：如图，延长CD 至点H ，使CD =DH ，连接AH ，∵CD 是AB 边上的中线，∴BD =AD ，在△CDB 和△HDA 中，∵CD =DH ，∠CDB =∠ADH ，BD =DA ，∴△CDB ≌△HDA （SAS ），∴BC =AH =a =6，在△ACH 中，AC -AH <CH <AC +AH ，∴10-6<2CD <10+6，∴2<CD <8．【点睛】本题主要考查了全等三角形的判定和性质，整式乘法和二元一次方程组的应用，三角形的三边关系，熟练掌握全等三角形的判定和性质，整式乘法法则，三角形的三边关系是解题的关键．10．（2022·新疆·乌鲁木齐市第四中学八年级期末）如图，在△ABC 中，AD 为BC 边上的中线，E 为AC 上的一点，BE 交AD 于点F ，已知AE =EF ．求证：AC =BF．【答案】见解析【分析】延长AD 到G ，使得DG =AD ，连接BG ，证明△ADC ≌△GDB （SAS ）得到AC =BG 且∠CAD =∠G ，再由等腰三角形的性质得到AE =EF ，继而证明BG =BF ，据此解题．【详解】证明：延长AD 到G ，使得DG =AD ，连接BG，在△ADC 和△GDB 中AD GD ADC GDB CD BD =⎧⎪∠=∠⎨⎪=⎩∴△ADC ≌△GDB （SAS ）∴AC =BG 且∠CAD =∠G∵AE =EF∴∠EFA =∠EAF∴∠G =∠EFA∵∠EFA =∠BFG∴∠G =∠BFG∴BG =BF∵AC =BG∴BF =AC【点睛】本题考查全等三角形的判定与性质、等边对等角、等角对等边等知识，是重要考点，难度一般，掌握相关知识是解题关键．11．（2021·山东威海·七年级期中）数学兴趣小组在活动时，老师提出了这样一个问题：如图1，在ABC 中，6AB =，10AC =，D 是BC 的中点，求BC 边上的中线AD 的取值范围．【阅读理解】小明在组内经过合作交流，得到了如下的解决方法：（1）如图1，延长AD 到E 点，使DE AD =，连接BE ．根据______可以判定ADC ≌△______，得出AC =______．这样就能把线段AB 、AC 、2AD 集中在ABE △中．利用三角形三边的关系，即可得出中线AD 的取值范围是．【方法感悟】当条件中出现“中点”、“中线”等条件时，可以考虑做“辅助线”——把中线延长一倍，构造全等三角形，把分散的已知条件和所求证的结论集中到同一个三角形中，这种做辅助线的方法称为“中线加倍”法．【问题解决】（2）如图2，在ABC 中，90A ∠= ，D 是BC 边的中点，90EDF = ∠，DE 交AB 于点E ，DF 交AC 于点F ，连接EF ，求证：222BE CF EF +=．【问题拓展】（3）如图3，ABC 中，90B = ∠，3AB =，AD 是ABC 的中线，CE BC ⊥，5CE =，且90ADE ∠= ．直接写出AE 的长＝______．【答案】（1）SAS ；EDB △；BE ；2<<8AD ；（2）见解析；（3）8．【分析】（1）根据三角形全等的判定方法和全等三角形的性质以及三角形三边的关系求解即可；（2）延长ED 使DG =ED ，连接FG ，GC ，根据垂直平分线的性质得到EF GF =，然后利用SAS 证明BDE CDG ≌，得到BE CG =，B DCG ∠=∠，进而得到18090ACG A ∠=︒-∠=︒,最后根据勾股定理证明即可；（3）延长AD 交EC 的延长线于点F ，根据ASA 证明ABD FCD ∆∆≌，然后根据垂直平分线的性质得到AE CF =，最后根据全等三角形的性质求解即可．【详解】解：（1）在ADC 和EDB △中，AD ED ADC EDB CD BD =⎧⎪∠=∠⎨⎪=⎩∴()ADC EDB SAS ≌△△，∴10AC BE ==．∵6AB =，∴<<BE AB AE BE AB -+，即106<<106AE -+，∴4<<16AE ，∴4<2<16AD ，解得：2<<8AD ；故答案为：SAS ；EDB △；BE ；2<<8AD ；（2）如图所示，延长ED 使DG =ED ，连接FG ，GC，∵90EDF = ∠，∴EF GF =，在BDE 和CDG 中，BD CD BDE CDG DE GD =⎧⎪∠=∠⎨⎪=⎩∴()BDE CDG SAS ≌△△，∴BE CG =，B DCG ∠=∠，∴AB CG ∥，∴18090ACG A ∠=︒-∠=︒，∴在Rt FGC △中，222CG FC FG +=，∴222BE CF EF +=；（3）如图所示，延长AD 交EC 的延长线于点F，∵,AB BC EF BC ⊥⊥，ABD FCD ∴∠=∠，在ABD △和FCD 中，ABD FCD BD CD ADB FDC ∠=∠⎧⎪=⎨⎪∠=∠⎩()ABD FCD ASA ∴∆∆≌，∴3CF AB ==，AD DF =，∵90ADE ∠= ，∴AE EF =，∵538EF CE AB =+=+=，∴8AE =．【点睛】此题考查了全等三角形的性质和判定方法，三角形的三边关系，“中线加倍”法的运用，解题的关键是根据题意作出辅助线构造全等三角形．12．（2020·北京·八年级单元测试）阅读下面材料：数学课上，老师给出了如下问题：如图，AD 为△ABC 中线，点E 在AC 上，BE 交AD 于点F ，AE =EF ．求证：AC =BF．经过讨论，同学们得到以下两种思路：完成下面问题：（1）①思路一的辅助线的作法是：；②思路二的辅助线的作法是：．（2）请你给出一种不同于以上两种思路的证明方法（要求：只写出辅助线的作法，并画出相应的图形，不需要写出证明过程）．【答案】（1）①延长AD至点G，使DG＝AD，连接BG；②作BG＝BF交AD的延长线于点G；（2）见解析【分析】（1）①依据SAS可证得△ADC≌△GDB，再利用AE=EF可以进一步证得∠G=∠FAE=∠AFE=∠BFG，从而证明结论；②作BG=BF交AD的延长线于点G，利用AE=EF可证得∠G=∠BFG=∠AFE=∠FAE，再依据AAS可以进一步证得△ADC≌△GDB，从而证明结论；（2）作BG∥AC交AD的延长线于G，证明△ADC≌△GDB（AAS），得出AC=BG，证出∠G=∠BFG，得出BG=BF，即可得出结论．【详解】解：（1）①如图①，延长AD至点G，使DG＝AD，连接BG，∵AD为△ABC中线，∴BD=CD，在△ADC和△GDB中，∵AD=GD，∠ADC=∠GDB，CD=BD，∴△ADC≌△GDB（SAS），∴AC=BG，∵AE=EF，∴∠CAD=∠EFA，∵∠BFG=∠G，∠G=∠CAD，∴∠G=∠BFG，∴BG=BF，∴AC=BF；②如图②，作BG＝BF交AD的延长线于点G，∵BG=BF，∴∠G=∠BFG，∵AE=EF，∴∠EAF=∠EFA，∵∠EFA=∠BFG，∴∠G=∠EAF，在△ADC和△GDB中，∵∠CAD=∠G，∠ADC=∠GDB，CD=BD，∴△ADC≌△GDB（AAS），。

倍长中线法知识网络详解：中线是三角形中的重要线段之一，在利用中线解决几何问题时，常常采用“倍长中线法” 增加辅助线．所谓倍长中线法，就是将三角形的中线延长一倍，以便构造出全等三角形，从而运用全等三角形的有关知识来解决问题的方法．倍长中线法的过程：延长某某到某点，使某某等于某某，使什么等于什么（延长的那一条），用 SAS证全等（对顶角）倍长中线最重要的一点，延长中线一倍，完成SAS全等三角形模型的构造。

【方法精讲】常用辅助线增加方法——倍长中线AAB CD △ ABC中方式1：延长AD到E，AD 是 BC 边中线使DE=AD，B C连接BED方式 2：间接倍长AFB D CEEA作 CF⊥ AD于 F，M 延长 MD到N，D作 BE⊥ AD的延长线于 E B 使 DN=MD，C连接 BEN连接 CN经典例题讲解：例 1：△ ABC中， AB=5， AC=3，求中线AD 的取值范围例2：已知在△ ABC 中， AB=AC，D 在 AB 上， E在 AC的延长线上， DE 交 BC 于 F，且DF=EF，求证： BD=CEADBCFE例 3：已知在△ ABC 中， AD 是 BC 边上的中线， E 是 AD 上一点，且BE=AC，延长 BE 交 AC于F，求证： AF=EFAFEBD C例 4：已知：如图，在ABC 中， AB AC ，D、E在BC上，且DE=EC，过D作 DF // BA交AE于点 F， DF=AC.A求证： AE 均分BACFB D E C例5：已知 CD=AB，∠ BDA=∠BAD，AE 是△ ABD的中线，求证：∠ C=∠ BAEAB CE D自检自测：1、如图，△ ABC中， BD=DC=AC,E是 DC的中点，求证， AD 均分∠ BAE.2、在四边形 ABCD中， AB∥ DC， E 为 BC边的中点，∠ BAE=∠EAF， AF 与 DC 的延长线订交于点 F。

试试究线段 AB 与 AF、 CF之间的数量关系，并证明你的结论 .ADBE CF3、如图，AD 为ABC 的中线，DE均分BDA 交AB于E，DF均分ADC 交AC于F.求证：BE CF EFAEFB CD第 14 题图4、已知：如图， ABC中， C=90 ， CM AB 于 M ，AT 均分 BAC交 CM 于 D，交 BC 于 T，过 D 作DE//AB 交 BC 于 E，求证： CT=BE.MAD BETC。

三角形中线的几种用法一、加倍法加倍法是三角形中线的最基本最常见的用法，其基本思路是：把三角形一边的中线延长，并截取中线长，得到二倍的三角形的中线长，利用三角形全等或中心对称，证明有关线段（或角）的相等及不等关系．基本模式是：如图1，已知：△ABC 中，AD 是BC 边上的中线，延长AD 至E ，使DE=AD ，则有：△ADC ≌△EDB ，BE ∥AC ，BE=AC ．例题 已知：如图2，AD 为△ABC 的中线，BE 交AC 于E ，交AD 于F ，且AE=EF ， 求证：AC=B Ｆ．证明：延长AD 至H ，使DH=AD ，则△ACD ≌HBD(SAS)，AC=BH ，∠HAC=∠H ∵AE=EF ，∴∠AFE=∠AEF ，由∠BFH=∠AFE 得∠BFH=∠H ，∴BF=BH ，∴AC=BF ．ͼ 1E DC BAͼ 2H FE DCBA二、利用三角形的中线把三角形分成面积相等的两部分来解决有关面积的求解问题基本模式是：若AD 为△ABC 中线，则S △ABD=S △ADC=21S △ABC ．例题 已知：如图3，△ABC 中，M 是AB 中点，MD ⊥BC ，EC ⊥BC ，S △ABC=24，求S △BDE ． 解：连接MC ，由题意知：DM ∥EC ，∴S △DME=S △DMC ，又∵M 为AB 中点，∴S △BCM=21S △ABC ，∴S △BDE=S △BCM=21S △ABC=12．三、关于“直角三角形斜边上中线等于斜边一半”的用法基本模式：如果CD 是Rt △ACB 斜边AB 上的中线，则有：CD=21AB ．例题 已知：如图4，∠ABC=∠ADC=90°，点M 、N 分别是对角线AC 、BD 的中点， 求证：MN ⊥BD ．证明：连结BM 、DM ，则由∠ABC=90°，M 为AC 的中点，得：BM=21AC ， 同理：由∠ADC=90°， M 为AC 的中点，得：MD=21AC ，∴BM=DM ，由N 为BD 中点及等腰三角形三线合一性质，得MN ⊥BD ．四、关于三角形重心问题的应用基本模式是：若O 为△ABC 的三条中线AD 、BE 、CF 的交点（即△ABC 的重心），则有OD OA =OE OB =OF OC =12．例题 已知：如图5，线段PQ 过△ABC 的重心M ，P 、Q 分别内分AB 、AC 的比值为p 、q ，求p 1+q 1．解：作射线AM 交BC 于D 点，分别过B 、C 两点作PQ 的平行线交AM 于G 、F ，∵M 为△ABC 的重心，∴DB=DC ，MD AM=2：1，∴△BDG ≌△DCF ，∴DG=DF ．。