高三数学定积分及其应用PPT教学课件

格式：ppt
大小：132.50 KB
文档页数：19

下载文档原格式

定积分及其应用ppt课件

n
xi 0, f (i )xi 0, i 1
|| T || max{x1, x2 , , xn }
n
b

lim
||T ||0
i 1
f (i )xi

f ( x)dx 0.
a
性质5的推论：（定积分不等式性质）
（1）如果在区间[a, b]上 f ( x) g( x)，
则
b
a
f
(
x
)dx

b
a
g(
x)dx.
(a b)
证明 f ( x) g( x), g( x) f ( x) 0,
b
a[g( x) f ( x)]dx 0,
(a b)
即
b
g( x)dx
b
f ( x)dx 0,
a
a
于是
b
a f ( x)dx

c
b
f
(
x)dx
c
b
a f ( x)dx c f ( x)dx.
（定积分对于积分区间具有可加性）
性质4
b
b
a 1 dx a
dx b a .
性质5 如果在区间[a, b]上 f ( x) 0，
则
b
a
f
(
x
)dx

0.
(a b)
证明 f ( x) 0, f (i ) 0, (i 1,2,,n)
前
积取负号．

a

y f (x)
b
b
特别，当 f (x) 1 时，有a 1 dx (b a)1 b a .

《高数》定积分课件

《高数》定积分ppt 课件
目录
• 定积分的概念 • 定积分的计算 • 微积分的应用 • 定积分的物理应用 • 定积分的进一步理解
01
CATALOGUE
定积分的概念
定积分的定义
01
定积分是积分的一种，是函数在区间上积分和的极限。
02
定积分常用于计算平面图形的面积、体积等。
03
定积分的定义基于极限思想，通过分割、近似、求和、取极限等步骤来定义。
物体在重力作用下的功与能
总结词
通过定积分计算重力做功和能量变化
详细描述
在重力作用下，物体运动过程中重力所做的功和能量变化可以用定积分表示。通过定积分计算，可以得出重力做功和能量变化的具体数值。
05
CATALOGUE
定积分的进一步理解
定积分的极限思想
定积分是通过对曲线下的面积进行极限分割，再求和得到的结果，这个过程体现了极限的思想。
可加性
对于任意分割的两个区间上的定积分，其和等于两区间上定积分的和。
区间区间上定积分的值之和。
比较性质
如果函数在不同区间上单调增加或减少，则其定积分的值也相应增加或减少。
02
CATALOGUE
定积分的计算
微积分基本定理
总结词
微积分基本定理是定积分计算的基础，它建立了积分与微分的联系，为解决定积分问题提供了重要的思路和方法。
另一个函数的定积分进行计算。这些方法在实际应用中具有广泛的应用价值。
积分中值定理
总结词
积分中值定理揭示了定积分与被积函数之间的关系，它是解决定积分问题的一个重要工具。
详细描述
积分中值定理指出，对于连续函数f(x)在闭区间[a,b]上的定积分∫baf(x)dx=f(ξ)(b−a) ，其中ξ∈[a,b]。这个定理说明了定积分的结果等于被积函数在一个子区间上的取值与该区间长度的乘积。这个定理在解决定积分问题时非常有用，特别是当我们需要找到被

高中数学定积分的概念课件PPT课件

5
观察下列演示过程，注意当分割加细时，矩形面积和与曲边梯形面积的关系．
6
7
观察下列演示过程，注意当分割加细时，矩形面积和与曲边梯形面积的关系．
8
观察下列演示过程，注意当分割加细时，矩形面积和与曲边梯形面积的关系．
9
观察下列演示过程，注意当分割加细时，矩形面积和与曲边梯形面积的关系．
14
观察下列演示过程，注意当分割加细时，矩形面积和与曲边梯形面积的关系．
15
求由连续曲线y=f(x)对应的曲边梯形面积的方法
(1)分割:在区间[0,1]上等间隔地插入n-1个点,将它等分成
n个小区间:a, x1,x1, x2,L xi1, xi ,L ,xn1,b,
每个小区间宽度⊿x b a
yf (x)
24
探究:
根据定积分的几何意义,如何用定积分表示图中阴影部分的
面积?
y
yf (x)
b
b
S S1 S2
a
f (x)dx
g(x)dx
a
b
S1
ya
fg((x))dx
b
S2
g ( x)dx
a
O aa
bx
25
三: 定积分的基本性质
性质1.
b
b
a kf ( x )dx ka f ( x )dx
1.5.3 定积分的概念
1
观察下列演示过程，注意当分割加细时，矩形面积和与曲边梯形面积的关系．
2
观察下列演示过程，注意当分割加细时，矩形面积和与曲边梯形面积的关系．
3
观察下列演示过程，注意当分割加细时，矩形面积和与曲边梯形面积的关系．
4
观察下列演示过程，注意当分割加细时，矩形面积和与曲边梯形面积的关系．

六章定积分应用ppt课件

WF(ba)
F
a
b
若F 为变力，力对
物体所作的功W=？
例1 带电量为q0与q1的正电荷分别放在空间两点，求当q1沿a与b连线从a移到b时电场力所作的功。
解: 如图建立坐标系：在上述移动过程中，电场
对q1作用力是变化的。
(i)取r为积分变量，则 r[a,b] q0
q1
(ii)相应于[a,b]上任一小区间[r,r+dr] o a
br
的功元素
dW Fdrkq0q1dr
(iii)所求功
r2
W
b
k
a
qr0q21dr
kq0q1
(1) r
b a
kq0q1(1ab1)
例2 在底面积为S的圆柱形容器中盛有一定量的气体。在等温条件下，由于气体膨胀，把容器中的一个活塞（面积为S）从点a推移至b，计算在移动过程中气体压力所作的功。
解: 如图建立坐标系，活塞位置可用坐标x表示。
引力
问题的提出：从物理学知道，质量分别为m1、m2，相
距为r的两质点间的引力大小为
F Gmr1m2 2
其中G为引力系数，引力的方向沿着两质点的连线。
如何计算一根
细棒对一个质点的引力F=？
r
o
m1
m2 x
例6 设有一长度为l、线密度为的均匀细棒，在
其中垂线上距棒a单位处有一质量为m 的质点M。
试计算该棒对质点M的引力。
x
问题的解决方法：定积分元素法
以液面为y轴，x轴铅直向下。
设平板铅直位于液体中形状如图。
o
距离液面x、高为dx、宽为f(x) 的
矩形平板所受压力的近似值，即压力元素为
a x x+dx

高等数学第六章第二节定积分在几何学上的应用课件.ppt

解:
cos x 0,
2
x
2
s
2
2
2 2 0
1 y2 dx 1 ( cos x)2 dx
2 2
2 cos x dx
0
2
2
2
2
sin
x 2
2
0
4
的弧长.
例11. 计算摆线
一拱
的弧长 .
y
解: ds
(dd
x t
)2
(
d d
y t
)
2
d
t
o
a2 (1 cos t)2 a2 sin2 t d t
1 y2 dx
因此所求弧长
s b 1 y2 dx a
b
a
1 f 2(x) dx
y
y f (x)
ds
o a xxdxb x
(2) 曲线弧由参数方程给出:
弧长元素(弧微分) :
ds (dx)2 (dy)2
2 (t) 2 (t) dt
因此所求弧长
s
2 (t) 2 (t) d t
(3) 曲线弧由极坐标方程给出:
y b
o x ax
则 V 2 a y2 dx 0
(利用对称性)
2
b2 a2
a
(a
2
x2
)
dx
0
2
b2 a2
a2 x
1 3
x3
a 0
4 ab2
3
方法2 利用椭圆参数方程
则 V 20a y2 dx 2 ab2 sin3t d t
2 ab2 2 1
3
4 ab2
3
特别当b
=
a

《高数定积分》课件

05
广义积分及其收敛性判别法
广义积分的概念及分类
广义积分的定义
广义积分是相对于正常积分而言的一种特殊积分，其积分区间可能包含无穷大或者无界函数。
广义积分的分类
根据被积函数和积分区间的不同，广义积分可分为无穷限广分的收敛性判别法
比较判别法
通过比较被积函数与已知收敛或发散的函数，来判断广义积分的收敛性。
换元法求解定积分
01
换元法的基本思想
通过变量代换简化定积分的计算。
02
常见的换元方法
03
换元法的注意事项
三角函数代换、倒代换、根式代换等。
代换后需调整积分上下限，并验证代换的可行性。
分部积分法求解定积分
分部积分法的基本思想
将复杂函数拆分为简单函数进行积分。
常见的分部积分公式
幂函数与三角函数、幂函数与指数函数、幂函数与对数函数等。
06
定积分在经济学等领域的应用
由边际函数求原经济函数
边际函数与定积分的关系
边际函数描述的是经济量变化的瞬时速率，而定积分则可用于求取原经济函数，即总量函数。
求原经济函数的步骤
首先确定边际函数的表达式，然后根据定积分的定义，对边际函数进行积分，得到原经济函数的表达式。
示例
已知某产品的边际收益函数为MR(q)，通过对其进行定积分，可以得到总收益函数 TR(q)。
曲线的长度、图形的面积等。
THANKS
感谢观看
原函数与不定积分概念
原函数定义
原函数是指一个函数的导数等于给定函数的函数。根据微积分基本定理，不定积分就是求原函数的过程。
不定积分性质
不定积分具有线性性质、常数倍性质和积分区间可加性。这些性质在求解复杂函数的定积分时非常有用。

《数学定积分的应用》课件

线性性质
定积分具有线性性质，即对于两个函数的和或差的积分，可以分别对每个函数进行积分后再求和或求差。
区间可加性
定积分具有区间可加性，即对于任意两个不重叠的区间[a, b]和[b, c]，有 ∫(a,c)f(x)dx=∫(a,b)f(x)dx+∫(b,c)f(x)dx。
积分中值定理
如果函数f(x)在区间[a, b]上连续，那么至少存在一个点ξ∈[a, b]，使得∫(a,b)f(x)dx=f(ξ)(b-a)。
电路中的电流和电压
要点一
总结词
定积分在电路分析中用于计算电流和电压，通过求解电路中的微分方程，可以得到电流和电压的分布。
要点二
详细描述
在电路分析中，电流和电压的变化规律通常由微分方程描述。通过应用定积分，可以将电路中的电压和电流表示为时间的函数。然后通过求解这个微分方程，可以得到电流和电压在整个电路中的分布情况。
详细描述
对于曲线形构件，其质量可以通过定积分计算。首先，确定构件的材料密度分布，然后对密度函数在构件的体积上进行积分，得到构件的总质量。
引力场的强度
总结词
通过定积分计算引力场的强度
详细描述
在引力场中，物体受到的引力大小与物体质量成正比，与物体之间的距离的平方成反比。通过定积分计算在某一空间区域内的引力场强度，即在该区域内所有物体产生的引力对该点的合力。具体地，将引力函数在空间区域上进行积分，得到该区域内的引力场强度。
dx进行计算。
功和压力
总结词
定积分可以用于计算变力做功和压力。
详细描述
对于一个质点在力F(x)=f(x)*dx的作用下沿直线运动，力F所做的功可以通过计算定积分得出，公式为 ∫(b a) f(x) dx。

《高中定积分的应用》课件

总结词
定积分在计算曲线形状的质量分布方面具有广泛应用，有助于理解物体的重心和转动惯量等物理量。
详细描述
对于曲线形状的物体，我们可以通过定积分计算其质量分布，进而求出物体的重心和转动惯量。这对于分析物体的稳定性和运动特性具有重要意义。
电场强度与电势的计算
总结词
在电场分析中，定积分用于计算电场强度和电势，有助于深入理解电场的性质和分布。
详细描述
在解决涉及多个函数的定积分问题时，需要仔细分析这些函数之间的关系，如一个函数可能对另一个函数求导或积分，或者两个函数之间存在特定的关系等。
复杂几何形状的分析与计算
总结词
对复杂几何形状的深入分析是解决问题的必要步骤。
详细描述
在解决涉及复杂几何形状的定积分问题时，需要深入理解几何形状的特点，如面积、体积等，并能够运用适当的公式进行计算。同时，还需要理解如何将复杂的几何形状分解为更简单的部分，以便于解决定积分问题。
详细描述
在经济学中，边际分析通过计算边际成本、边际收益和边际利润等指标，帮助企业决策者判断生产、定价和销售等方面的最优策略。弹性分析则通过计算需求价格弹性、供给价格弹性等指标，分析市场价格的变动对需求和供给的影响，进而影响市场均衡和资源配置。
成本与收益计算
总结词
成本与收益计算是经济学中重要的财务分析工具，用于评估企业的经营绩效和投资回报。
THANK YOU
定积分的几何意义
总结词
定积分的几何意义有助于直观理解定积分的应用。
详细描述
定积分的几何意义表示一个曲线下的面积。通过计算定积分，可以求出曲线下某个区间上的面积，从而解决一些实际问题，如求物体的质量、速度等。
定积分的计算方法

高等数学-定积分及其应用ppt课件.ppt

一、引例
在变速直线运动中, 已知位置函数
与速度函数
之间有关系:
物体在时间间隔
内经过的路程为
这种积分与原函数的关系在一定条件下具有普遍性 .
5.3 定积分的计算
则积分上限函数
证:
则有
定理1. 若
5.3.1 牛顿 – 莱布尼兹公式
说明:
1) 定理 1 证明了连续函数的原函数是存在的.
2) 变限积分求导:
5.6.1 广义积分
引例. 曲线
和直线
及 x 轴所围成的开口曲
边梯形的面积
可记作
其含义可理解为
1 连续函数在无限区间上的积分
定义1. 设
若
存在 ,
则称此极限为 f (x) 在区间的广义积分,
记作
这时称广义积分
收敛 ;
如果上述极限不存在,
就称广义积分
发散 .
类似地 , 若
公式, 复化求积公式等,
并有现成的数学软件可供调用.
性质1 常数因子可提到积分号外性质2 函数代数和的积分等于它们积分的代数和。
5.2 定积分的简单性质
性质3 若在区间 [ a , b ]上 f (x)≡K，则性质4 定积分的区间可加性若 c 是 [ a , b ] 内的任一点，则
的面积 .
解:
例3. 汽车以每小时 36 km 的速度行驶 ,
速停车,
解: 设开始刹车时刻为
则此时刻汽车速度
刹车后汽车减速行驶 , 其速度为
当汽车停住时,
即
得
故在这段时间内汽车所走的距离为
刹车,
问从开始刹
到某处需要减
设汽车以等加速度
车到停车走了多少距离?

《定积分及其应用》课件

在经济学中，供需关系决定了市场的价格。供需曲线的面积表示市场上供应和需求的关系。通过计算这个面积，我们可以了解市场的均衡点，也就是市场上的价格。同时，通过观察供需曲线面积的变化，我们可以了解市场的价格变动趋势。
感谢您的观看
THANKS
在曲线上的积分。
曲线的转动惯量
总结词
通过定积分计算曲线的转动惯量
详细描述
转动惯量是描述物体转动难易程度的物理量。对于一个均匀细长的物体，其转动惯量可以通过定积分来计算。转动惯量等于质量分布相对于某一轴的转动惯量，等于质量密度函数在物体质量分布上的积分。
05
定积分的经济应用
收益流的现值
总结词
收益流的现值是定积分在经济中的一个重要应用，它可以帮助我们计算未来的现金流在当前的价值。
详细描述
在金融和经济学中，我们经常需要考虑未来的收益流，也就是未来的现金流。由于货币的时间价值，我们需要将未来的现金流折现到现在的价值。定积分可以用来计算这种折现的值。
投资决策问题
总结词
投资决策问题涉及到如何分配有限的资源以获得最大的回报。定积分可以用来解决这类问题。
定积分的几何意义
总结词
定积分的值等于函数图像与x轴所夹的面积。
详细描述
定积分的值可以通过几何意义来解释，即定积分的值等于函数图像与x轴所夹的面积。这个面积可以是正的、负的或零，取决于函数图像在给定区间上的上下位置。
定积分的性质
总结词
定积分具有线性性质、可加性、可减性和区间可加性等性质。
详细描述
体积的计算
总结词
定积分在计算三维空间中物体体积的问题中起到关键作用，特别是对于旋转体和薄片绕旋转轴旋转形成的体积。
VS

《定积分及其应用》课件

性质
1 线性性质
定积分的线性性质使得我们能够对函数的和、差、乘以常数进行积分。
2 区间可加性
在一个区间上的积分等于在多个子区间上的积分之和。
3 保号性质
当函数在一个区间上不改变符号时，其定积分保持正负性质。
计算方法
换元法
通过变量代换，将原本复杂的积分转化为简单的积分。
分部积分法
将原本难以求解的函数积分转换成两个易于求解的函数之积分。
定积分的应用
通过物理、经济学相关实例展示定积分在实际中的应用价值。
总结与回顾
在本课件中，我们深入学习了定积分的定义、性质、计算方法以及应用。希望这些知识能够帮助你更好地理解和应用定积分，在解决实际问题中发挥重要作用。
《定积分及其应用》PPT 课件
欢迎大家来到本次关于《定积分及其应用》的PPT课件，本课件将带领你深入探索定积分的世界，揭示其定义、性质、计算方法以及广泛的应用。让我们开始这个精彩的学习之旅吧！
定义
定积分代表曲线和x轴之间的面积，可以看作是无穷多个微小的面积的累加。
区别。
应用
几何意义
定积分可以计算曲线和x轴之间的面积，可以应用于计算图形的面积、弧长、体积等。
物理应用
定积分可以应用于物理学中的速度、加速度、质量等问题的求解。
经济学应用
定积分可以应用于经济学中的边际效应、总收益、总成本等的分析和计算。
综合实例展示
曲线的定积分
通过实际例子展示如何计算曲线和x轴之间的定积分。

《高等数学教学课件》07定积分应用PPT资料59页

A 2(1y25y2)dy 12
| 2
12(14y2)dy2(y4y3)
1 2
2
0
3 03
1 .求 t使 y x 2 (x 0 ),y t,y 轴所围图形面积与 y x 2 ,y t,x 1 所围图形面积之和最小 . 2.在第一象限 yx2,y2x2,y1围一平面图形 .求a使 yax2将该图形分成面积相等两部分 .
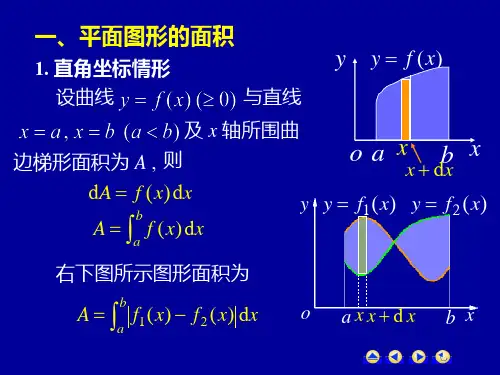
根据定积分的定义和几何意义知
b
f(x)0A f(x)dx;
b
f(x)0 A f(x)dx;
a
a
一般A
b
f(x)dx;
a
(2 )由曲线 yf(x ),yg (x )和直线 xa ,xb 所围成的面积 A .f(x )g (x )
b
Aa[f(x)g(x)]dx
特 , g ( 别 x ) f(x ) x [a ,b ]
长度为 xk xk xk1; 任取 k [ xk1 , xk ],
n
构造和式 :
f (k )xk ,
k 1
记
max 1k n
xk
,
n
如果和式极限
lim
0 k1
f(k)xk
存在,则
称f(x)在[a,b]上可积,并且称此极限值为
f(x) 在[a,b]上的定积分.
b
记作: f ( x )dx a
1 1
(1, 1) x2
2
1
A
1
(x
)d x
x
o
1
x
2
| x2
23
( lnx) ln2

定积分及其应用(高数) PPT课件

定理2 设 u( x),v( x)在区间[a,b]上有连续的导数,
则
aabbuuddvvu[uvvba]ba
bb
vvdduu
aa
定积分的分部积分公式
由不定积分的分部积分法及N--L公式.
类似于不定积分的分部积分法：“反、对、幂、指、三”
（3）重要公式
奇、偶函数在对称区间上的定积分性质三角函数的定积分公式周期函数的定积分公式
方的面积取正号; 在 x 轴下方的面积取负号.
A1 A2
A3 A4
b
a f ( x)dx
A1 A2
A3
A4
2.定积分的性质
性质1
b
a [
f
(
x)
g(
x)]dx
b
a
f
(
x)dx
b
a g(
x)dx
性质2
b
a kf
(
x)dx
k
b
a
f
(
x)dx
( k 为常数)
性质3 （区间可加性）
b
c
b
a f ( x)dx a f ( x)dx c f ( x)dx
区间上的定积分都相等.
例1 设
f
(
x)
2 5
x
0
x
1
,
求
1 x2
2
0
f
( x)dx.
解
2
0
f
( x)dx
1 0
f
( x)dx
2
1
f
( x)dx
1
2xdx
2
5dx
6.
0
1
例2 求

高等数学定积分及其应用78页PPT

高等数学定积分及其应用
6
、
露
凝
无
游
氛
，
天
高
风
景
澈
。
7、翩翩新来燕，双双入我庐，先巢故尚在，相将还旧居。
8
、
吁
嗟
身
后
名
，
于
我
若
浮
烟
。
9、陶渊明（约 365年 —427年），字元亮，（又一说名潜，字渊明）号五柳先生，私谥“靖节”，东晋末期南朝宋初期诗人、文学家、辞赋家、散
1
0
、
倚
南
窗
以
寄
傲，审Fra bibliotek容膝
之
易
安
。
21、要知道对好事的称颂过于夸大，也会招来人们的反感轻蔑和嫉妒。——培根 22、业精于勤，荒于嬉；行成于思，毁于随。——韩愈
文家。汉族，东晋浔阳柴桑人（今江西九江）。曾做过几年小官，后辞官回家，从此隐居，田园生活是陶渊明诗的主要题材，相关作品有《饮酒》、《归园田居》、《桃花源记》、《五柳先生传》、《归去来兮辞》等。
23、一切节省，归根到底都归结为时间的节省。——马克思 24、意志命运往往背道而驰，决心到最后会全部推倒。——莎士比亚
25、学习是劳动，是充满思想的劳动。——乌申斯基
谢谢！

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

例3 求下列极限值：
（1）lim 1 [ s in s in 2 s in ( n 1 )]
n n n n
n
111 1
（2）lim ( )
n n 1n 2n 3 2 n
【解题要点】构造特定形式和→确定被积函数和积分区间→用定积分表示极限.
考点3 定积分中参数的取值问题
（4） 3|x2 1|dx ； 0
（5） e1 lnxdx . 1x
例2 计算下列定积分：
b
（1） (a x)(x b)dx(b＞a)； a
（2） 5(3x34|x|sinx)dx. 5
【解题要点】确定被积函数的原函数→对被积函数作适当变形→将定积分转化为求曲边梯形的面积.
考点2 利用定积分概念求极限值
a
a
a
（3） c f( x ) d x b f( x ) d x b f( x ) d x.
a
c
a
5.微积分基本定理：
如果f(x)在区间[a，b]上的图象是一条连续不断的曲线，并且 F(x) f(x)，则
bf(x)dx F (b) F (a)
a
Hale Waihona Puke 拓展延伸1.用极限逼近原理求曲边梯形面积是定积分的实际背景，其基本思路是：分割→近似替代→求和→取极限.
物体，在a≤t≤b时段内行驶的路程
b
s
v(t)dt
a
（2）如果物体在变力F(x)的作用下做直线运动，并且物体沿着与F(x)相同的方向从x＝a移动到x＝b(a＜b)，则变力F(x)
b
所作的功W F(x)dx a
4.定积分的运算性质：
b
b
（1） kf(x)d x k f(x)d x；
a
a
b
b
b
（2） [f ( x )g ( x ) ] d x f ( x ) d x g ( x ) d x
的最大值.
y
BA
D
O
x
例11 若过原点的直线l与曲线C： y＝x2－4x(x≥0)所围成图形的面积为36，求直线l的方程.
【解题要点】作几何直观图选择面积算法→确定积分变量、被积函数和积分区间→将非规则曲边梯形分割或补形为规则曲边梯形→ 对多边形面积直接套公式求解.
考点6 定积分在物理中的应用
2.定积分是一个特定形式和的极限，其几何意义是曲边梯形的面积，定积分的值由被积函数，积分上限和下限所确定.
3.在实际问题中，定积分可以表示面积、体积、路程、功等等，求定积分的值有定义法、几何法、定理法三种，有时利用定积分的性质进行计算，能简化解题过程.
4.位于x轴下方的曲边梯形的面积，等于相应定积分的相反数.一般地，由直线x＝a，x＝b(a＜b)，y＝0和曲线y＝ f(x)所围成的曲边梯形的面积
x叫做积分变量，f(x)dx叫做被积式.
2.定积分的几何意义：
如果函数f(x)在区间[a，b]上的图象是一条连续不断的曲线，且f(x)≥0，那么
b
定积分 f(x)dx 表示由直线x＝a，x＝ a
b(a＜b)，y＝0和曲线y＝f(x)所围成的曲边梯形的面积.
3.定积分的物理意义：
（1）以速度v＝v(t)作变速直线运动的
＋3所围成图形的面积.
例9 求直线y＝x－4与曲线y2＝2x所围成图形的面积.
例10 如图，曲线C1：y＝x2与曲线C2： y＝－x2＋2ax(a＞1)交于点O，A，直线
x＝t(0＜t≤1)与曲线C1、C2分别相交于点D、B，连结OD，DA，AB.设a为常数，
当t变化时，求曲边四边形ABOD的面积S
S b|f(x)|dx a
5.由直线x＝a，x＝b(a＜b)和曲线 y＝f(x)，y＝g(x)所围成的曲边梯形的
面积 S b|f(x) g(x)|dx a
考点分析
考点1 定积分的基本运算
例1 计算下列定积分：
（1） 2x(x 1)dx ； 0
（2） 2(e2x 1
x1)dx ；
（3） sin2xdx； 0
例12 两车站A，B相距7.2km，一辆电车从A站开往B站，电车开出ts后到达途中C点，这一段速度为1.2t(m/s)，到C点的速度为24m/s.从C点到B点前的D点以等速行驶，从D点开始刹车，经ts后速度为 (24－1.2t)m/s，在B点恰好停车，求：（1）A，C两点间的距离；（2）B，D两点间的距离；（3）电车从A站到B站所需的时间.
10.3 定积分及其应用
知识梳理
t
p
1 2
5730
1.定积分的有关概念：
把
n
lim
n
i1
bnaf(
i)
叫做函数f(x)在区间
b
[a，b]上的定积分，记作 f(x)dx ,即
b
f(x ) d x
a
n lim in 1bn a f(i) a.其中a与b分
别叫做积分下限与积分上限，区间[a，b]
叫做积分区间，函数f(x)叫做被积函数,
x
例6 求函数 f(x) sin t(1c o st) d t 0
的值域.
例7 已知函数 f(x)x(12lnt)dt
1
2t
(x＞1)，试推断函数f(x)是否有零点.
【解题要点】求积分函数的解析式→据有关原理分析函数性质.
考点5 用定积分求平面图形的面积例8 求直线y＝x＋3与曲线y＝x2－2x
例4 (08年山东卷）设函数
f(x) a x2 c(a 0 )，若
1f(x)dx
0
f(x0)，0≤x0≤1，则x0的值
为
.
例5 设f(x)＝kx＋b，已知
1
f(x)dx 1，且
1f2(x)dx 4，
0
0
求k的取值范围.
【解题要点】求相关定积分值→利用方程或不等式思想分析参数取值.
考点4 定积分中的函数问题

高三数学定积分及其应用PPT教学课件

合集下载

定积分及其应用ppt课件

《高数》定积分课件

高中数学定积分的概念课件PPT课件

最新[数学]第五章定积分及其应用_第1节_定积分的概念与性质教学讲义ppt课件

六章定积分应用ppt课件

高等数学第六章第二节定积分在几何学上的应用课件.ppt

《高数定积分》课件

《数学定积分的应用》课件

《高中定积分的应用》课件

高等数学-定积分及其应用ppt课件.ppt

《定积分及其应用》课件

《定积分及其应用》课件

《高等数学教学课件》07定积分应用PPT资料59页

定积分及其应用(高数) PPT课件

高等数学定积分及其应用78页PPT

文档推荐

最新文档

高三数学定积分及其应用PPT教学课件

合集下载

定积分及其应用ppt课件

《高数》定积分课件

高中数学 定积分的概念课件PPT课件

最新[数学]第五章定积分及其应用_第1节_定积分的概念与性质教学讲义ppt课件

六章定积分应用ppt课件

高等数学第六章第二节定积分在几何学上的应用课件.ppt

《高数定积分》课件

《数学定积分的应用》课件

《高中定积分的应用》课件

高等数学-定积分及其应用ppt课件.ppt

《定积分及其应用》课件

《定积分及其应用》课件

《高等数学教学课件》07定积分应用PPT资料59页

定积分及其应用(高数) PPT课件

高等数学 定积分及其应用78页PPT

文档推荐

最新文档

高中数学定积分的概念课件PPT课件

高等数学定积分及其应用78页PPT