当前位置：文档之家 › 单自由度系统受迫振动(b)汇总

单自由度系统受迫振动(b)汇总

  • 格式：ppt
  • 大小：2.82 MB
  • 文档页数：63

下载文档原格式

  / 63

合集下载

振动理论及其应用：第2章_单自由度系统受迫振动

振动理论及其应用：第2章_单自由度系统受迫振动

1
2s
1 s2
x
F0 k
ei(t )
Aei(t )
A B 稳态响应的实振幅
若： F (t) F0 cost
则： x(t) Acos(t )
2020年12月9日 <<振动力学>>
无阻尼情况：
x(t) B 1 s2
eit
F0 k
1 1 s2
eit
7
单自由度系统受迫振动 / 简谐力激励的强迫振动
（5）对于有阻尼系统， max并不 出现在s=1处，而且稍偏左
d 0
ds
max 2
s
1
1 2
1 2 2
2020年12月9日 <<振动力学>>
(s)
5
0
0.1
4
3
0.25
0.375
2
0.5
1
1
s
0
0
1
2
3
x F0 ei(t ) Aei(t )
k
14
单自由度系统受迫振动 / 稳态响应的特性
• 稳态响应特性
(s)
1
(1 s2 )2 (2s)2
(s)
5
0
0.1
4
（6）当 1/ 2 振幅无极值
1
3
2
1
0.25 0.375
0.5 1
s
0
0
1
2
3
2020年12月9日 15
受力分析
振动微分方程： mx cx kx F0eit
2x02为0年复12月数9日变量，分别与 F0 cost 和 F0 sin t 相对应 4 <<振动力学>>

振动力学4单自由度受迫

振动力学4单自由度受迫
2
F0
= H (ω ) F0
k − mω + icω = re
2 2 2
iϕ
• 有： r = (k − mω ) + (cω )
x = xe
_ iωt
cω ϕ = arctan k − mω 2
F0 i (ωt −ϕ ) F0 e i (ωt −ϕ ) = e = r (k − mω 2 ) 2 + (cω ) 2
X = X 0ω 0
2 2
(ω 0 − ω 2 ) 2 + ( 2ζω 0ω ) 2
=
X0 (1 − s 2 ) 2 + ( 2ζ s ) 2
tan ϕ =
2ζω 0ω 2ζs = ω0 2 − ω 2 1 − s 2
单自由度系统受迫振动—线性阻尼系统简谐激振
• 相频特性曲线
• 当频率比s等于1时，相角为 2 。 • 利用相位判断共振：共振相位法。 • 利用振幅判断共振：共振幅值法。
=
X0 (1 − s 2 ) 2 + ( 2ζ s ) 2
2ζω 0ω 2ζs = ω0 2 − ω 2 1 − s 2
2ζs 1− s2
单自由度系统受迫振动—线性阻尼系统简谐激振
• 结论 （1）线性系统对简谐激励的稳态响应是频率等同
于激振频率）线性系统对简谐激励的稳态响应是 频率等同于激振频率、而相位滞后激振力的简谐 振动 （2）稳态响应的振幅及相位只取决于系统本身的物 理性质（m, , k, , c）和激振力的频率及力幅，而 与系统进入运动的方式（即初始条件）无关
H v (ω ) ：速度导纳 H a (ω ) ：加速度导纳
k − mω 2 + icω ：速度阻抗 Z v (ω ) = iω k − mω 2 + icω ：加速度阻抗 Z a (ω ) = − 2

单自由度强迫振动

单自由度强迫振动

3.1 单自由度系统在谐和 激振下的强迫振动
所谓谐和激励就是正弦或余弦激励。
设激励为 F(t)=F0sinwt ，这 里 w为激振频率，利用牛顿定 律并引入阻尼比x 可得到
F0 x 2wnx x w x sin wt m
2 n
第3章 单自由度系统强迫振动
3.1 单自由度系统在谐和激振下的强迫振动
xwnt
上述解的第一部分代表由初始条件引
起的自由振动;
第3章 单自由度系统强迫振动
3.1 单自由度系统在谐和激振下的强迫振动
7
第二部分
X 0e
xwnt
xwn sin w cos sin wd t sin cos wd t wd
代表由干扰力引起的自由振动。 这两部分都是衰减振动，随时间的推移而消
失，称为瞬态响应或暂态响应；
最后只剩下第三部分
X 0 sin(w t ) ，代表
与激振力同形式的等幅的强迫振动，称为稳态响 应，这才是我们最关心的。
第3章 单自由度系统强迫振动
3.1 单自由度系统在谐和激振下的强迫振动
8
若为余弦激励, 则响应（解）为：
x0 xwn x0 xe sin wd t x0 cos wd t wd xw t xwn cos w sin X 0e sin wd t cos cos wd t wd
第3章 单自由度系 统强迫振动
第3章 单自由度系统强迫振动
1
系统在外部激励作用下的振动称为受
迫振动或强迫振动。
自由振动只是系统对初始扰动 ( 初始
条件)的响应。由于阻尼的存在,振动现象
很快就会消失。

17-4 单自由度系统的无阻尼受迫振动

17-4 单自由度系统的无阻尼受迫振动

单自由度系统的无阻尼受迫振动工程中的自由振动由于阻尼的存在而逐渐衰减，最后完全停止 实际上又存在大量不衰减的持续振动，由于外界有能量输入补 充阻尼的消耗，例如外加激振力。

在外加激振力作用下的振动称为受迫振动。

k m 交流电通过电磁铁产生交变的电磁力引起振动系统； 弹性梁上的电动机由于转子偏心在转动时引起的振动。

)sin(ϕω+=t H F 简谐激振力是一种典型的周期变化的激振力： H ：激振力力幅；ω：激振力的圆频率；φ：激振力初相位简谐激振力 F 在坐标轴上投影为： )sin(ϕω+=t H F)sin(22ϕω++−=t H kx dt x d m m k n =2ωm H h =kxF k −=1.振动微分方程 m k F F k m x O x图示振动系统，物块质量m 。

取平衡位置为原点，向下为正.)sin(222ϕωω+=+t h x dtx d n 恢复力F k 在坐标轴上投影： 两端除以m ，并设： 物块受恢复力F k 和激振力F 。

质点运动微分方程为：则得： 该式为 无阻尼受迫振动微分方程的标准形式)sin(222ϕωω+=+t h dtx d n 二阶常系数非齐次线性微分方程21x x x +=)sin(1θω+=t A x n )sin(2ϕω+=t b x 解由两部分组成： 齐次方程的通解为: 将x 2代入无阻尼受迫振动微分方程，得：)sin()sin()sin(22ϕωϕωωϕωω+=+++−t h t b t b n 22ωω−=n h b )sin()sin(22ϕωωωθω+−++=t h t A x n n b 为待定常数设特解为： 得无阻尼受迫振动微分方程的全解：解得：表明：无阻尼受迫振动是由两个谐振动合成的：第一部分是频率为固有频率的自由振动；第二部分是频率为激振力频率的振动，称为受迫振动。

实际振动系统存在阻尼，自由振动部分会很快衰减掉，我们着重研究第二部分受迫振动，它是一种稳态振动。

振动理论04(3)-单自由度系统受迫振动

振动理论04(3)-单自由度系统受迫振动

振动理论(4-3)第四章单自由度的受迫振动陈永强北京大学力学系振动的隔离原理●机械或者其他原因产生的振动常常是不可避免的，但是通过适当的措施可以把影响降低到最小●隔振系统的作用是保护特定对象免受传过来的过大振动(被动隔振)，或者防止过大的振动力传递到周围环境（主动隔振）●这两个方面本质上是相同的，都是试图降低传递的振动力振动的隔离原理00000/()st x x kx x P k P TR ======弹簧力传递力传递比外力外力k通过弹簧传给下层结构的力012345-1－2-3-41A BCω/ωn振动的隔离原理：无阻尼012345-1－2-3-41A BCω/ωn传递比大于1如果无阻尼情况下2振动的隔离原理: 阻尼考虑阻尼的影响，传递的力包括两部分：弹簧力和阻尼力，分别与位移和速度同相而具有的相位差传递比振动的隔离原理: 阻尼ω/ωn10201230.250.50.5c /c c =0●区域中，阻尼使可传性减小(但仍然比1大)●,传递比小于1，阻尼的存在使可传性更差2●阻尼的存在可以有效防止共振●阻尼的不利效应可以很容易通过使弹簧变得更软来弥补在不改变传动比的情况下如何降低隔离质量的振幅可以把附放在一个大的质量上, 同时增加弹簧的刚度，保持不变。

由方程可以看到，由于的增大，将降低632014/10/22例题●一机器质量为，支承在总刚度为的弹簧上。

机器上的非平衡旋转部件在转速为3000 rpm时导致的扰动力. 假定阻尼比为, 试确定(a) 非平衡导致的运动振幅；(b) 传递比；(c) 传递的力●解：系统的静挠度为19811411−3m141mm其固有频率为=1332Hz系统的振幅为m=0.0379mm642014/10/22●传递比●传递的力=扰动力传递比N652014/10/22复频率响应●继续讨论系统激励(输入)与响应(输出)关系和描述●振动微分方程可以看成是矢量平衡投影⏹竖直轴投影⏹水平轴投影●把谐振激励表示为●位移记为cωx0mω2x0x0ϕωP0kx0●把复位移向量带入微分方程●可以求得●定义复频率响应(输出与输入的比值)容易看出，依赖于频率比和阻尼因子。

第三讲(单自由度系统受迫振动)

第三讲(单自由度系统受迫振动)

四、单自由度系统在周期性激励作用下的受迫振动 1、谐波分析与叠加原理 2、傅立叶（Fourier）级数法 五、单自由度系统在任意激励作用下的受迫振动 1、脉冲响应函数法或杜哈梅（Duhamel）积分法 2、傅立叶（Fourier）变换法 3、拉普拉斯（Laplas）变换法
三、简谐激励下的受迫振动 1、简谐激励下的受迫振动响应及频谱分析 2、受迫振动的复数求解法－－单位谐函数法 3、支座简谐激励（位移激励）引起的振动与被动隔振 4、偏心质量（力激励）引起的振动与主动隔振 5、测振传感器的基本原理
汽车振动学
第三讲
2009年3月2日
汽车振动学
第二章 单自由度系统的振动 （8学时）
2009年1月
第二章 单自由度系统的振动
一、单自由度振动系统 1、振动微分方程的建立 2、振动等效系统及外界激励 3、振动微分方程的求解 二、单自由度系统的自由振动 1、无阻尼系统的自由振动 2、有阻尼系统的自由振动 三、单自由度系统在简谐激励作用下的受迫振动 1、简谐激励下的受迫振动响应及频谱分析 2、受迫振动的复数求解法－－单位谐函数法 3、支座简谐激励（位移激励）引起的振动与被动隔振 4、偏心质量（力激励）引起的振动与主动隔振 5、测振传感器的原理
其中
X β = = X0
1 (1 − λ 2 ) 2 + (2ζλ ) 2
称为放大因子
代表稳态响应振幅与最大静位移之比，它不仅随频率比而变，而且随阻尼比而变。 如果系统无阻尼，则系统的振动响应为 自由振动响应 受迫振动响应
F0 λ F0 x = x0 cos ωnt + sin ωn t − sin ωnt + sin ωt 2 2 k (1 − λ ) k (1 − λ ) ωn & x0

单自由度系统强迫振动汇总

单自由度系统强迫振动汇总
称为稳态振动。
x2(t) Bsin( pt )
1.3 简谐激振力引起的强迫振动
x2(t) Bsin( pt ) 代入 x 2nx 2 x hsin pt
h B
( 2 p2 )2 4n2 p2
tan
2np 2 p2
特解：
x2(t)
h
sin( pt )
( 2 p2 )2 4n2 p2
全解：
稳态响应： x2(t) Bsin( pt )
B
h ( 2 p2 )2 4n2 p2
简谐激振力引起的振动的全解：
tan
2np 2 p2
右端第一项是齐次解，代表衰减的自由振动；由于瞬态振动会很快衰 减而停止，我们在研究强迫振动问题时主要关心它的稳态振动解。
第二项是特解，代表由激振力引起的稳态强迫振动，位移响应是一简谐 运动，其频率与激振力的频率相同，但稳态响应的相位滞后于激励相位。
讨论影响振幅、相位差的因素：
mx cx kx H sin pt
x 2nx 2 x hsin pt x2(t) Bsin( pt )
B
( 2
h p2 )2
4n2 p2
h
2
1
1
p
2
2
2
n
p
2
B0
1 2 2 22
静力偏移 相对阻尼系数 频率比
激振力的幅 值引起的静
变形
1.3 简谐激振力引起的强迫振动
（单自由度系统）
1.1 无阻尼自由振动—简谐运动 1.2 有阻尼自由振动—衰减运动 强迫振动：系统在持续的外界激励作用下产生的振动。
强迫振动从外界不断获取能量来补偿阻尼所消耗的能 量，使系统维持持续的振动。
外界激励周期激励简F (谐t 激T )励

《理论力学 动力学》 第九讲 单自由度系统的无阻尼受迫振动

《理论力学 动力学》 第九讲 单自由度系统的无阻尼受迫振动

单自由度系统的受迫振动理论曾凡林哈尔滨工业大学理论力学教研组本讲主要内容1、单自由度系统的无阻尼受迫振动2、单自由度系统的有阻尼受迫振动1、单自由度系统的无阻尼受迫振动受迫振动在外加激振力作用下的振动称为受迫振动。

km简谐激振力是一种典型的周期变化的激振力。

简谐激振力随时间的变化关系可写成：)sin(j w +=t H F 其中：H 称为激振力的力幅，即激振力的最大值；ω是激振力的角频率；j 是激振力的初相角。

（1）振动微分方程m 取物块的平衡位置为坐标原点，x 轴向下为正。

物块的受力为恢复力F e 和激振力F 。

F e F方程两边同除以m ，并令, 得到：m k =20w H h m=)sin(d d 2022j w w +=+t h x tx ——无阻尼受迫振动微分方程的标准形式解可以写成：12xx x =+x 1 对应齐次方程的通解; x 2 对应的是特解。

齐次方程的通解可写为：)sin(01q w +=t A x 特解可写为：2sin()x b t w j =+将x 2 代入微分方程，得到:)sin()sin()sin(22j w j w w j w w +=+++-t h t b t b 解得：220ww -=hb 微分方程的全解为：)sin()sin(2200j w ww q w +-++=t ht A x 结果表明：无阻尼受迫振动是由两个谐振动合成的。

第一部分是频率为固有频率的自由振动；第二部分是频率为激振力频率的振动，称为受迫振动。

第一部分会逐渐衰减，而第二部分则是稳定的。

0sin()A t w q +220sin()ht w f w w+-1、单自由度系统的无阻尼受迫振动（2）受迫振动的振幅2220sin()hx t w j w w=+-系统的受迫振动为简谐振动，振动频率也等于激振力的频率，振幅大小与运动的初始条件无关，而与振动系统的固有频率ω0、激振力的频率ω、激振力的力幅H 相关。

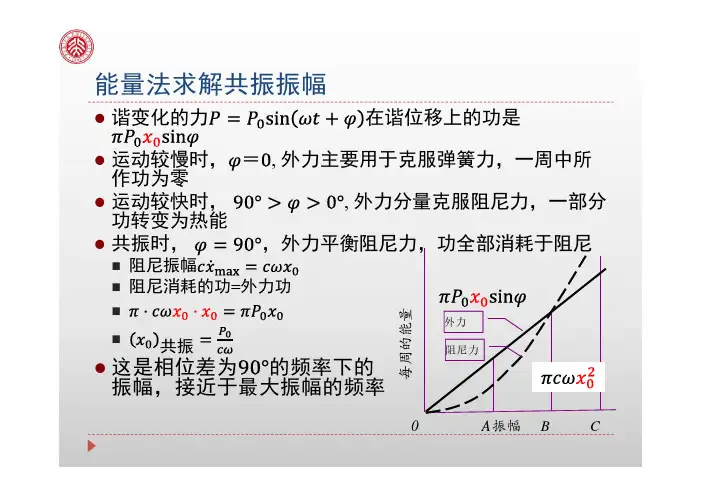
振动理论04(2)-单自由度系统受迫振动

振动理论04(2)-单自由度系统受迫振动

●谐变化的力在谐位移上的功是●运动较慢时，＝, 外力主要用于克服弹簧力，一周中所作功为零●运动较快时，, 外力分量克服阻尼力，一部分功转变为热能●共振时，，外力平衡阻尼力，功全部消耗于阻尼⏹阻尼振幅⏹阻尼消耗的功=外力功⏹⏹共振●这是相位差为的频率下的振幅，接近于最大振幅的频率能量法求解共振振幅每周的能量振幅外力阻尼力0A B C共振时的放大因子共振另一方面，有阻尼振动的对数衰减率近似为 共振时的放大因子用对数衰减率表示为瞬态振动和稳态振动瞬态振动稳态振动特解例题汽车重千克，装在四只弹簧上，在车身重量作用下弹簧下压厘米，四只缓冲器，每只在1厘米/秒的速度时具有阻尼系数千克。

把车子和四只车轮一起安装在一个试验台上，实验台以共振速率上下运动，振幅为厘米。

假定中心时在轴距中心处，试求车身在弹簧上的振幅。

解：rad具有振幅的弹簧顶部的运动相当于在质量上具有振幅的力kgcm●假定弹簧质量体系，由旋转机械的不平衡运动激励，只能竖向运动●不平衡部分用一个离心质量表示，离心距为，角速度为●表示非旋转部分的位移(以静平衡位置为参考)，的运动可以表示为考虑阻尼影响的转动失衡2014/10/2232运动平衡方程sinsin这个方程与具有振幅的弹簧顶部运动导致的振动方程是一样的,令, 可直接得到振动的振幅tan332014/10/22进一步，可以写成如下的无量纲关系tan342014/10/22转动失衡受迫振动幅频和相频特性352014/10/22●前面的例子是旋转不平衡发生在单一平面内，现在讨论在几个平面内的平衡情况●静不平衡⏹不平衡质量都在同一平面内，合力是一个单一的径向力⏹这种不平衡可以用静态试验测出来，即把轮-轴架在轨道上，使其停留在某个位置：重心在轴的下方⏹不用转动轮子就可以测得不平衡位置●动不平衡⏹不平衡出现在多个平面内⏹合力是一个集中力和一个摇摆力矩⏹通过旋转转子才能测出转子失衡2014/10/2236平衡机一般来讲，比较长的转子，例如马达的电枢或者汽车的发动机的机轴，汽车的轮毂和轮胎，都可以认为是一系列薄盘组成，每个薄盘都带有不同程度的失衡⏹用于检测并修正转子失衡的机器叫平衡机⏹平衡机包含弹性支承用于通过运动检测不平衡力⏹测得支承振动幅度和相对相位，进而确定转子的不平衡量并进行修正⏹这是一个二自由度问题：转子的平动和转动是同时发生的372014/10/22●在设计机械具体实施上述原理的检测过程的时候，会采用各种振动传感器、光电传感器，测量其振动情况和转速同步信号，确定失衡重点的位置，然后根据需要对转子进行加重法和去重法的对转子进行平衡加工⏹加重法：在不平衡相反方向配上校正重块。

第三章 单自由度系统受迫振动分析

第三章 单自由度系统受迫振动分析

（5）对于有阻尼系统， max并不 出现在s=1处，而且稍偏左
d 0
ds
max 2
s
1
1 2
1 2 2
2020年8月6日 <<振动力学>>
(s)
5
0
0.1
4
3
0.25
0.375
2
0.5
1
1
s
0
0
1
2
3
x F0 ei(t ) Aei(t )
k
14
单自由度系统受迫振动 / 稳态响应的特性
• 稳态响应特性
当 0
(s)
0
0
1
2
3
结论：共振 振幅无穷大
但共振对于来自阻尼的影响很敏感，在 s=1 附近的区域内，
增加阻尼使振幅明显下降
2020年8月6日 <<振动力学>>
x F0 ei(t ) Aei(t )
k
13
单自由度系统受迫振动 / 稳态响应的特性
• 稳态响应特性
(s)
1
(1 s2 )2 (2s)2
2020年8月6日 3
<<振动力学>>
单自由度系统受迫振动 / 简谐力激励的强迫振动
• 线性系统的受迫振动
• 简谐力激励的强迫振动
F (t )
F (t )
x
弹簧－质量系统
设 F (t) F0eit F0 外力幅值
外力的激励频率
m
0
k
c
m mx
kx cx
实部和虚部分别与 F0 cost 和 F0 sin t 相对应
受力分析
振动微分方程： mx cx kx F0eit

单自由度系统受迫振动

单自由度系统受迫振动

s
0 1 2 3
0
结论：响应的振幅很小
0
F0 i (t ) x e Aei (t ) k
C2.14
§2.1.2 稳态响应的特性
(s)

0
0 .1
( s)
1 (1 s 2 ) 2 (2s) 2
5 4 3 2 1
（3）在以上两个领域 s>>1，s<<1
1 0
1 2
0
s
0
阻尼越弱，Q越大，带 宽越窄，共振峰越陡峭
F0 i (t ) x e Aei (t ) k
C2.19
§2.1.2 稳态响应的特性
( s)
以s为横坐标画出 ( s) 曲线 2 s ( s ) arctan 1 s2 相频特性曲线 （1）当s<<1（ 0） 相位差 0
C2.16
§2.1.2 稳态响应的特性
( s)
1 (1 s 2 ) 2 (2s) 2
5 4 3 2
(s)

0
0 .1
max 并不 （5）对于有阻尼系统， 出现在s=1处，而是稍偏左
d 0 ds
max
0.25 0.375 0 .5 1
s 1 2 2
1 2 1 2
180
90
0 0
s
1 2 3
位移与激振力在相位上几乎相同
（2）当s>>1（ 0 ）
π
（3）当
位移与激振力反相
s 1
0
π 共振时的相位差为 2 ，与阻尼无关
F0 i (t ) x e Aei (t ) k C2.20

振动力学第二章第二节单自由度系统的受迫振动

振动力学第二章第二节单自由度系统的受迫振动
受迫振动系统的稳态响应为
x B sin(t )
1. 激振力 FS H sin t
周期 T 2π
WH
T
0
FS
dx dt
(t ) d t
T
0
H
sintB cos(t
)dt
HB
2
T
0
[s
in
(2t
)
s in ]d t
π BH
s in
在系统发生共振的情况下，相位差 π ，激振力在
一周期内做功为 WH π BH，做功最多。2
3. 弹性力 FE kx 做的功
WE
T
dx
0
FE
(t)
dt
dt
T
Bk sin(t )B cos(t ) d t
0
kB2
2
T
0
sin
2(t
)d
t
0
表明弹性力在一个振动周期内做功之和为零。
能量曲线
在一个振动周期内激振力做功之和等于阻尼力消耗的能量
WH WR
2.1 简谐激励作用下的受迫振动
已知简谐激振力 FS H sin t
稳态受迫振动的响应为 x B sin(t )
dx dt
B
cos(t
),
d2 x dt2
B
2
sin(t
)
应用达朗贝尔原理，将弹簧质量系统写成
m
d2 dt
x
2
c
dx dt阻尼力 弹性力 激振力
现将各力分别用 B、kB、cB、H、m 2 B 的旋转矢量表示。
d2 x dt2
2n
dx dt
pn2 x
h sin t
x(0) x0和v(0) v0

单自由度系统受迫振动__1

单自由度系统受迫振动__1

可见，形心O1的运动轨迹为一个圆
动挠度: f x 2 y 2 e1
es 2
(1 s 2 ) 2 ( 2s ) 2
主动隔振系数
＝
隔振后传到地基的力幅值 隔振前传到地基的力幅值
隔振前
m
隔振前机器传到地基的力：
隔振后
F0e
it
F0e
it
m c
F0eit
隔振后通过k、c传到地基上的力:
k
F1 F0
隔振系数:
1 (2s) 2 i[t (1 2 )] e (1 s 2 ) 2 (2s) 2
t
o1
x
l/2 o l/2
C
y
o1
x
x
质心运动定理：
d2 m 2 ( x e cost ) kx cx dt d2 m 2 ( y e sin t ) ky cy dt
右端项可看作激振力旋转矢量 m e 2 e it 在 x 和 y 方向上的投影，作用点C，方 向沿CO1
单自由度系统受迫振动 / 工程中的受迫振动问题
• 转子的临界转速
气轮机、发电机等高速旋转机械在开机或停机过程中经过某一 转速附近时，支撑系统经常会发生剧烈振动

临界转速 在数值上很接近转子横向振动的固有频率 以单盘转子为例 转轴质量不计 圆盘质量 m 圆盘质心 C 固定在转轴中部 形心 O1 偏心距 CO1＝e
1. 小阻尼情况下，通解为
x(t ) e
0t
(c1 cosd t c2 sin d t )
x(t ) A sin(t )
2. 假定为正弦激励，特解可设为 代入微分方程，得
则振动系统总响应为

第3章 单自由度系统的受迫振动

第3章 单自由度系统的受迫振动
值得注意，系统共振时，阻尼对相位差无影响，即无论阻尼多大，当ω ＝ pn 时，相位差ϕ 总是等
于 90°。在振动实验中，常以此作为判断振动系统是否处于共振状态的一种标志。 (3) 高频区。当λ>>1, ϕ＝180°。表明当激振力频率远远高于固有频率时，受迫振动的相位差接
近与 180°。这说明受迫振动的位移与激振力是反相位的。 应当指出，对于λ＝0，当λ<1 时，λ =0；λ>1 时，ϕ＝180°；λ＝1 时，ϕ角从 0 跳到 180°。 对于不同的阻尼值，相位差ϕ角在 0 到180° 之间变化。 例 3-1 质量为 M 的电机安装在弹性基础上。由于转子不均衡，产生偏心，偏心距为 e，偏心质
pn
(3-10)
绘出对应不同的阻尼比ζ，相位差ϕ随λ变化的曲线族如图 3-2 中的右上角所示，即相频特性曲线。
(1) 低频区。当λ<<1时，ϕ≈0，表明当激振力频率很低或ω<< pn 时，相位差ϕ接近于零，即受
迫振动的位移与激振力几乎同相位。
(2) 共振区。当λ=1时，ϕ＝90°。表明当激振力频率等于振动系统的固有频率时，相位差为 90°。
根据达朗贝尔原理，有
− cx& + Mg − k(x + δ st ) − M&x& − meω 2 sin ωt = 0
∴ M&x& + cx& + kx = −meω 2 sin ωt
令
p
2 n
=
k M
，2n
=
c M
，则上式可写成
&x& +
2nx&
+
pn2 x

振动理论-第3章 单自由度系统的强迫振动

振动理论-第3章 单自由度系统的强迫振动

x0 0
、
x0
n
F0 k
1
r r
2
则初始条件为：
x0 0
x0
n
F0 k
r 1 r2
讨论：
x(t
)
C1
cos
nt
C2
sin
nt
F0
m(n2
2
)
cos
t
x(0) x0
C1
x0
F0 k
1
1 r
2
x(0) x0
C2
x0
n
故全解：
x(t)
x0
cos nt
x0
n
sin
nt
F0 k
1
1 r
2
cos nt
a
复数的三角函数表示：Z Z cos i sin
复数的指数函数表示：Z Z ei
对于复数域内复函数 H () a() ib() A() iB()
可表示为 H () H () ei ()
H ()
a2 b2 A2 B2
() arctan Im[H ()] Re[H ()]
二. 激励力引起的强迫振动
n
2
2
2
n
2
激励与响应的相位角
arctan
2
n
1
n
2
或写为：
X st
1
1 r 2 2 2 r 2
arctan
2 r
1 r2
st
F0 k
r n
系统的最大静位移 频率比
所以，强迫振动的稳态解为：
x2
F0 k
1
sin(t )
1 r 2 2 2 r 2

振动理论讲义第4章 单自由度系统受迫振动

振动理论讲义第4章 单自由度系统受迫振动

(4.6)
前面两项是无阻尼自由振动，第三项是无阻尼受迫振动。 方程(4.6)的前两项是具有固有频率 的正弦波，而第三项受迫振动的正弦波的频率 是外来激励的频率 。显然，这两个频率是相互完全独立的。(4.6)是由两个正弦波叠加 而成，合成之后的波不再是简谐运动。 进一步分析(4.5)式表示的含义。显然， 波，该振幅取决于频率比 。 是一个具有振幅为 的正弦
第4章 单自由 由度系统 统受迫振动 4.1 前 前言
前面 面讨论的是 是在外界初始 始干扰下依 依靠系统本身 身的弹性恢 恢复力维持的 的振动。下 下面将讨 论系统由外界持续 续激振引起的振动。 强迫振动从外 强 外界不断获 获取能量来补 补偿阻尼所 所消耗的 能量，使系统得以 以维持持续的等幅振动 动。 响应：外界激振引 引起的系统 统的振动状态 态。对于不 不同的外界激 激励，系统 统具有不同的 的响应， 一般以位 位移形式表 表达，有时也以速度或 或加速度的形式来表达 达。
4.2 无 无阻尼受迫 迫振动
首先 先研究简单 单的情况，使 使单自由度 度振动方程的 的阻尼项为 为零，得到如 如下方程 kx P0 sin mx n t 观察可知函数 x x0 sin t 可以满足这个方程 程，代入上式，有
2
(4.1)
(4.2)
振动理论
x0 k m 2 P0
北京大学力学系 陈永强


或者
x0 P0 P0 / k P0 / k 2 2 k m 1 m / k 1 2 / n2
代回(4.2)，有
x P0 / k sin t 1 2 / n2
(4.3)
即为所求的位移响应。上面方程中的 P0 / k 具有简单的物理意义：荷载 P0 作用下的弹簧 的静变形。如果记
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

2
1 (2s)2 (1 s2 )2 (2s)2
1 2
2 tg 1(2s)
4
单自由度系统受迫振动 / 工程中的受迫振动问题
偏心质量情况
m
e t
me2 sin t
m
M
x
x
e
M t
x
k
c
k
c
k
ck
2
2
Mx cx kx me2 sin t
解2：x(t) 1B1 sin(t )
1
s2
(1 s2 )2 (2s)2
6
单自由度系统受迫振动 / 工程中的受迫振动问题
s2
A1
D
(1 s 2 )2 (2s)2
s 0
A1 还可写为：
A1
1
D 2
(
(1 s2 )2 (2s)2
02
)
m
k
c
s 0 0
机器外壳
lim
s0
A1
1
02
(D 2 )
D2 ：被测物体的加速度幅值
当仪器的固有频率远大于外壳振动频率时，仪器读数的幅值
1
1 (2s)2
2s 1 (2s)2
cos(t
1)]
D
1 (2s)2 (1 s2 )2 (2s)2
sin(t
1
2 )
D
sin(t
)
令： sin2
2s 1 (2s)2
cos2
1
1 (2s)2
2 tg 12s
令： 1 2
2020年10月3日
1 (2s)2 (1 s2 )2 (2s)2
和前述支承运动中 的绝对位移法结果 相同
10
单自由度系统受迫振动 / 工程中的受迫振动问题
• 工程中的受迫振动问题
• 惯性式测振仪 • 振动的隔离 • 转子的临界转速
2020年10月3日 11
单自由度系统受迫振动 / 工程中的受迫振动问题
• 振动的隔离
将作为振源的机器设备与地基隔离，以减少对环境的影响称为 主动隔振
机械振动理论
单自由度系统受迫振动
2020年10月3日 1
教学内容
• 线性系统的受迫振动 • 工程中的受迫振动问题 • 任意周期激励的响应 • 非周期激励的响应
2020年10月3日 2
• 工程中的受迫振动问题
• 惯性式测振仪 • 振动的隔离 • 转子的临界转速
2020年10月3日 3
单自由度系统受迫振动 / 工程中的受迫振动问题
另一种分析方法
基础位移假定为正弦: x f D sin t
x 取绝对位移
m
动力学方程 ：
k
c
xf
mx c(x x f ) k(x x f ) 0
x(t) kD k
(1
1 s2)2
(2s)2
sin(t
1 )
cD
k
(1
1
s2 )2 (2s)2
cos(t
1 )
(1
s2
D )2
(2s)2
回顾：
支承运动情况 基座位移规律 ：
x f (t) Deit
x
m0
x1
k
c
xf
x1
k
xf
m
c
x
相对位移
绝对位移
m1x1 cx1 kx1 mD 2eit
x x1 xf 2Dei(t )
x1
De i(t1 ) 1
1(s)
s2
(1 s2 )2 (2s)2
1
(s)
tg
1
2s
1 s2
2020年10月3日
k
c
隔振材料：k，c
F1 F0
(1
1 (2s)2 s2 )2 (2s)
2
ei[t
(1
2
)]
隔振系数：
F1max
F0
1 (2s)2 (1 s2 )2 (2s)2
＝ 主动隔振系数
隔振后传到地基的力幅值
隔振前传到地基的力幅值
隔振前机器传到地基的力：F0eit 隔振后系统响应：
隔振前
m
F0eit
隔振后
m
F0eit
x F0 ei(t1)
k
隔振材料：k，c k
c
A F0
k
2020年10月3日
1
(1 s2 )2 (2s)2
1
tg 1
2s
1 s2
12
单自由度系统受迫振动 / 工程中的受迫振动问题
mx cx kx mD2eit
振幅 ： A1
s2 D
(1 s2 )2 (2s)2
仪器
m
x
k
c
xf
机器外壳
低固有频率测量仪用于测量振 动的位移幅值，称为位移计
s 0
lim
s
A1
D
2020年10月3日
当仪器的固有频率远小于外壳振动 频率时，仪器读数的幅值 A1 接近 外壳振动的振幅 D
A1与外壳加速度的幅值成正比
高固有频率测量仪用于测量振动的加速度幅值，称为加速度计
2020年10月3日 7
单自由度系统受迫振动 / 工程中的受迫振动问题
另一种分析方法
基础位移假定为正弦: x f D sin t
x 取绝对位移
mx
m
m
k
c
受力图
k(xmx c(x x f ) k(x x f ) 0
ei[t
(1
2
)]
2 tg 12s
2020年10月3日
c
k
c 02m
c s
m 0
2
0
s
0
2s
13
单自由度系统受迫振动 / 工程中的受迫振动问题
＝ 主动隔振系数
隔振后传到地基的力幅值
隔振前传到地基的力幅值
隔振前机器传到地基的力： F0eit
隔振前
m
F0 e i t
隔振后
m
F0eit
隔振后通过k、c传到地基上的力：
x F0 ei(t1)
k
1
(1 s2 )2 (2s)2
1
tg 1
2s
1 s2
隔振后通过k、c传到地基上的力： 隔振前
F1 cx kx (ic k) F0 ei(t1)
k
m
F0eit
F0 (1 i2s)ei(t1)
隔振材料：k，c
隔振后
m
F0eit
k
c
F0
(1
1 (2s)2 s2 )2 (2s)2
解1：x(t) Bsin(t )
1
(1 s2 )2 (2s)2
2B0210年10mM月e3日 0
k M
s
0
tg 1
2s
1 s2
me 2
B k
5
单自由度系统受迫振动 / 工程中的受迫振动问题
• 惯性式测振仪
基础位移 x f Deit x ： m 相对于外壳的相对位移
动力方程 ： m(x xf ) cx kx 0
[sin(t
1 )
2s
cos(t
1 )]
2020年10月3日
c
k
c
2 0
m
c m
s
0
2 0
s
0
2s
1
tg
1
2s
1 s2
单自由度系统受迫振动 / 工程中的受迫振动问题
x(t)
(1
s2
D )2
(2s)2
[sin(t
1 )
2s
cos(t
1 )]
1
tg
1
2s
1 s2
D 1 (2s)2 (1 s2 )2 (2s)2 [sin(t 1)
mx cx kx cx f kxf kDsint cD cost
叠加原理，解为右端两项解之和 ：
x(t) kD k
(1
1 s2)2
(2s)2
sin(t
1 )
cD
k
(1
1
s2 )2 (2s)2
cos(t
1 )
2020年10月3日
1
tg 1
2s
1 s2
8
单自由度系统受迫振动 / 工程中的受迫振动问题