当前位置：文档之家 › 第四章_时变电磁场_miao

第四章_时变电磁场_miao

  • 格式：ppt
  • 大小：3.66 MB
  • 文档页数：71

下载文档原格式

  / 71

合集下载

电磁矢论 第四章、时变电磁场

电磁矢论 第四章、时变电磁场
上式称为洛伦兹规范。
注：电磁场论中另一种常用的规范是库伦规范 A 0，通常在
恒定磁场中应用。
4.2 电磁场的位函数
2、位函数的微分方程（达朗贝尔方程）
D H J t A B A, E t 2 A A A
即可得到坡印廷定理的微分形式：






1 1 E H E D H B E J t 2 2
再在任意闭合曲面S所包围的体积V上对上式两端进行积分， 并应用散度定理，即可得到坡印廷定理的积分形式：



S

过内导体表面进入每单位长度内导体的功率。
同轴线
4.3 电磁能量守恒定律（坡印廷定理）
解：（1）在理想导体中不存在电场和磁场，电场和磁场只存在 于内外导体之间的理想介质中。利用高斯定理和安培环路定理，容
易求得内外导体之间的电场和磁场分别为：
E e
I U a b , H e ln b a 2


2 2 2 t
4.2 电磁场的位函数
即：
A 2 A 2 J t
2
2 2 2 t
是洛伦兹规范下矢量位 A 和标量位 所满足的微分方程，
称为达朗贝尔方程。
4.2 电磁场的位函数
推导（由麦克斯韦方程组来推导）：
D D (1) H J E H E J E t t B B E H E H (2) t t

第4章时变电磁场

第4章时变电磁场

位函数的定义
B 0
B Ε t
B A
A ( Ε ) 0 t
A E t
上页
下页
返回
5 结束
满足下列变换关系的两组位函数 和 能描述同 （A、 ） （A、 ） 一个电磁场问题。 A A 为任意可微函数 t
空间区域V中的电磁能量：
1 1 W w dV ( E D H B)dV V V 2 2
特点：当场随时间变化时，空间各点的电磁场能量密度也要随
时间改变，从而引起电磁能量流动 电磁能量守恒关系：
进入体积V的能量＝体积V内增加的能量＋体积V内损耗的能量
上页
下页
返回
结束 12
坡印廷定理 表征电磁能量守恒关系的定理
波动方程
2 H H 2 0 t
2
电磁波动方程
上页
下页
返回
2 结束
推证
Ε H t H Ε t H 0 Ε 0
同理可得
2 E E 2 0 t
2
E H ( ) t
得到的电磁场矢量是相同的。
上页
下页
返回
10 结束
4.3
电磁能量守恒定律
讨论内容
电磁能量及守恒关系 坡印廷定理 坡印廷矢量
上页
下页
返回
结束 11
电磁能量及守恒关系 电场能量密度： 磁场能量密度：
1 we E D 2 wm 1 H B 2
dW dt
S
V
1 1 电磁能量密度： w we wm E D H B 2 2

第四章 时变电磁场共38页文档

第四章 时变电磁场共38页文档

当与回路交链的磁通发生变化时，回路中会产生感
应电动势，这就是法拉弟电磁感应定律。
电磁感应定律： e d
dt
负号表示感应电流产生的磁
场总是阻碍原磁场的变化。
B
e
S
图4.1.1 感生电动势的参考方向
第四章
四、磁通变化方式：
时变电磁场
1.动生电动势：导电回路与恒定磁场有相对运动（导 线切割磁力线），此种感应电势又名发电机电势（发 电机工作原理）。
电的磁磁场H 感都应J能定产律D 生：t 电麦场克lH 。斯d 韦l第二S(方J 程，D t)表d明S电全荷电和流定变律化
磁通连E续性原B理：表E明d磁l 场是无B 源场dS, 磁电力磁线感总应是定律闭
第四章
时变电磁场
电荷守恒定律
SJC d S q t tVd V V tdV
SJCd SV JC dV V tdV
JC
t
第四章
高斯通量定律的微分形式： D
时变电磁场
JC t t D D t
JC
D0 t
令
Jd
D t
为位移电流密度。
第四章
恒定场
电流连续性原理
①磁场力： d fdv qB
②感应场强：
df
Ei
vB dq
③感应电势：
eEidvBd
图4.1.3 发电机电动势
第四章
时变电磁场
2、感生电动势：导电回路不运动，回路交链的磁通随 时间变化，此种感应电势又名变压器电势（变压器工 作原理）。
ed mdB d S B dS
dt dS t
S t
第四章
时变场的知识结构框图：
高斯定律 磁通连续性原理

电磁波第四章-时变电磁场

电磁波第四章-时变电磁场
的能量，其方向为该点能量流动的方向
物理电子学院 周俊 第12页
坡印亭矢量(电磁能流密度矢量)： S E H (W / m 2 , 瓦 / 米 2 )
←描述时变电磁场中电磁能量传输的一个重要物理量 瞬时功率： S S ( t )
平均功率： S 1 T



1 S ( t )dt ， S av Re E H 2
2Ey x
2
2 E y
2Ey t
2
0
或

2Ey y
2

2Ey z
2

2Ey t
2
0
2 E z
2 Ez t
2
0
或
2 Ez x
2

2 Ez y
2

2 Ez z
2

2 Ez t
2
0
物理电子学院
周俊
第 4页
电磁场与电磁波 第四章__时变电磁场
2
2 2 2 的微分方程 t
若场量不随时间变化，波动方程蜕变为泊松方程
A J 2
2
▼第8页
电磁场与电磁波 第四章__时变电磁场
第三节 电磁能量守恒定律
1 电场能量密度： w e D E 2 1 磁场能量密度： w m B H 2 1 1 电磁能量密度： w w e w m D E B H 2 2
4.2.2 达朗贝尔方程 推导 A 和 的方程：
1 B A ←矢量位的定义： H A A A E ←标量位的定义： E t t

第4章 时变电磁场

第4章 时变电磁场
⇒ ∇× H =
B = ∇× A
E = −∇ϕ −
1 ∂E ∇×∇× A = J +ε µ ∂t ∂ ⎛ ∂A ⎞ −∇ ϕ − ⎜ ⎟ ∂t ⎝ ∂t ⎠
= J +ε
将矢量恒等式
∇ × ∇ × A = ∇ (∇ ⋅ A ) − ∇ 2 A
得 即
⎛ ∂ϕ ∇ ( ∇ ⋅ A ) − ∇ A = µ J − µε ∇ ⎜ ⎝ ∂t
2
2
∂2 A ⎞ ⎟ − µε ∂t 2 ⎠
∂2 A ∂ϕ ⎞ ⎛ J A ∇ A − µε = − µ + ∇ ∇ ⋅ + µε ⎜ ⎟ ∂t 2 ∂t ⎠ ⎝
◇ 由亥姆霍兹定理：一矢量由其散度和旋度确定。 ◇ 前面定义A 的旋度等于磁感应强度B。为确定矢量位A 还需规定其散度。 ∂ϕ ◇ 令 （洛仑兹条件) ∇ ⋅ A = − µε ∂t 所以 同理
)=
−H ⋅
∂B ∂D − E ⋅J − E ⋅ ∂t ∂t
)
∂D ∂t ∂ (ε E ) = E ⋅ ∂t 1 ∂ = (ε E ⋅ E 2 ∂t ∂ ⎛1 2 ⎞ = ⎜ εE ⎟ ∂t ⎝ 2 ⎠
E ⋅
)
E ⋅ J = σ E2
于是得
H ⋅ (∇ × E ) − E ⋅ (∇ × H
)= −
∂ → jω ∂t
∂2 ቤተ መጻሕፍቲ ባይዱ −ω 2 2 ∂t
二、复数形式的麦氏方程 由麦氏第一方程 设为时谐场
∇× H = J + ∂D ∂t
i i ⎡ ⎛ i jωt ⎞⎤ ⎡ ⎡ jωt ⎤ ⇒ ∇× ⎢ Re ⎜ Hm e ⎟⎥ = Re ⎢ J m e ⎥ + Re ⎢ jω Dm e jωt ⎤ ⎥ ⎠⎦ ⎣ ⎦ ⎣ ⎦ ⎣ ⎝

电动力学教程 第4章 时变电磁场

电动力学教程 第4章 时变电磁场

A 随时间变化为动态矢量位
A E t 0
也随时间变化称为动态标量位。
A E t
(6)
2. 达朗贝方程 将(5)和(6)式分别代入麦克斯韦方程组得 到A和满足的微分方程 ρ 2 A t ε
因此上式改写为：
1 1 E H H E E J E D H B t 2 t 2 利用矢量恒等式 E H H E H E E H
麦克斯韦方程的复数形式是分别对其实部和虚部进行的并不改变其实部和虚部的性质故在复数运算中对复数的微分和积分运算rererererererere其中l是实线性算子如等因此麦氏方程所有场变量都仅仅是空间的函数反映场的空间分布方程的解剩以时间因子e与含时的麦氏方程比较其复数形式实现了时空分离因此使方程的求解更简单
利用麦氏方程组可以导出Poynting矢量和Poynting定理 的表达式。
D H J t B E t D E H E J E t B H E H t
kE0 B ˆx H dt e cos(t kz ) 0 t 0 1
(2) S (t ) E(t ) H (t )
ˆy E0 cos(t kz ) e ˆx e
ˆz e
kE0 2
0
kE0
cos(t kz )
0
cos2 (t kz )
电荷分布场(标量场)中的电荷流（即电 流）及电荷流密度（即电流密度）
dq i , dt

第4章 时变电磁场


(2)
对方程（2）两边取旋度有 E H t 2 2 E H E E ( E ) E
E t
2
对于各向同性的介质，得
2 E 2 E 2 0 t (5)
E 0 t
t
同理可得
2 H 2 H 2 0 t (6)
第四章 时 变 电 磁 场
从上方程可以看出：时变电磁场的电场场量和磁场场量在 空间中是以波动形式变化的，因此称时变电磁场为电磁波。 上两式为关于场量 E、H 的矢量波动方程，表示时变电磁场 以波的形式在空间存在和传播，其波速为
A E ex Am cos(t kz ) t
第四章 时 变 电 磁 场
§4.3 电磁能量守恒定律
能量守恒定律是一切物质运动过程遵守的普遍规律，作为特殊形态的物 质，电磁场及其运动过程也遵守这一规律。 下面讨论电磁场的能量和能量守恒定律，引入重要的坡印廷矢量和坡印廷 定理，分析讨论电磁场能量、电荷电流运动及电磁场做功之间的相互联系。
其中Am、k是常数，求电场强度、磁场强度。
解：
Ax B A ey ey kAm cos(t kz ) z k H ey Am cos(t kz )
A 0 t

C
如果假设过去某一时刻，场还没有建立，则C=0。
量位只决定于ρ，这对求解方程特别有利。只需解出A，无需
解出 就可得到待求的电场和磁场。 电磁位函数只是简化时变电磁场分析求解的一种辅助函数，应 用不同的规范条件，矢量位A和标量位 的解也不相同，但最终 得到的电磁场矢量是相同的。

电磁场与电磁波课件之时变电磁场要点

E
H
能流密度矢量的瞬时值为
E
H
S (r , t ) E (r , t ) H (r , t )
S
可见，能流密度矢量的瞬时值等于电场强度 和磁场强度的瞬时值的乘积。
只有当两者同时达到最大值时，能流密度才达到最大。若某一时刻
电场强度或磁场强度为零，则在该时刻能流密度矢量为零。
在三维空间中仅需求解 4 个坐标分量。在直角坐标系中，实际上
等于求解 1 个标量方程。 必须指出的是，尽管磁感应强度在形式上只与磁矢势有关，不能
据此认为磁感应强度由磁矢势决定而与电标势无关。因为在时变情形
下，电磁场相互激发，而时变电场由磁矢势和电标势共同描述，使得 时变磁场本质上与磁矢势和电标势都有联系。
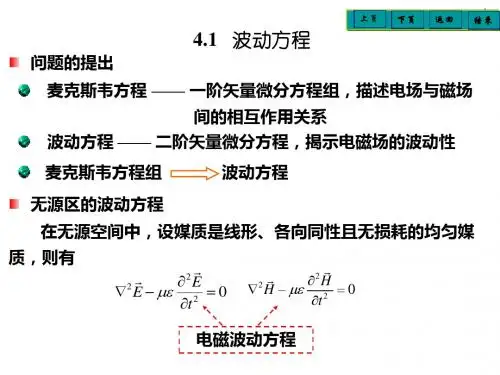
由麦克斯韦方程组微分形式
D H J t B E t B 0 D
E H t
0 H E
J 0
H E t H 0
E 0
则此区域中麦克斯韦方程为
, ,
E
H
V
D H J t B E t ( H ) 0 ( E ) 0
利用矢量恒等式 ( E H ) H E E H ，将上式代入
2 H 2 H 0 2 t 2 H 2 H 2 J t
P175
位函数方程为一个矢量方程和一个标量方程
2 A 2 A J 2 t
2 2 2 t
根据位函数定义式及麦克斯韦方程，得 2 A A J t 2 t A t

电磁场与电磁波课件ppt(电子科技大学)第四章 时变电磁场解析



A A J ( ) t t A ( A) 2 A 2 A 2 A 2 J ( A ) t t A 0 t 2 A 2 A 2 J t
除了利用洛伦兹条件外，另一种常用的是库仑条件，即 A 0
（洛仑兹条件是个定解条件。）
电子科技大学编写
高等教育出版社出版
电磁场与电磁波
第4章 时变电磁场
D E H B
E B J t
8
位函数的微分方程 （达朗贝尔方程） D H J t A B A E t
电子科技大学编写
高等教育出版社出版
电磁场与电磁波
第4章 时变电磁场
7
位函数的规范条件
造成位函数的不确定性的原因就是没有规定 A 的散度。利用 位函数的不确定性，可通过规定 A 的散度使位函数满足的方程得
以简化。 在电磁理论中，通常采用洛伦兹条件，即 A 0 t
第4章 时变电磁场
19
电磁能量在内外导体之间的介质中沿轴方向流动，即由电源向负 载，如图所示。
同轴线中的电场、磁场和坡印廷矢量 （理想导体情况）
穿过任意横截面的功率为
P S ez dS
S
b
教育出版社出版
电子科技大学编写
电磁场与电磁波
得到的电磁场矢量是相同的。
问题 若应用库仑条件，位函数满足什么样的方程? 具有什么特点?
电子科技大学编写
高等教育出版社出版
电磁场与电磁波
第4章 时变电磁场
11
4.3
电磁能量守恒定律 （重点）

第4章 时变电磁场与电磁波(时变电磁场)


物质方程
1）辅助方程——本构方程 D 0E P B 0 ( H M ) J E 2）对于各向同性的线性媒质，有 D E B H J E
媒质可分为均匀与不均匀、线性与非线性、各向同性与 各向异性之分。 1)若描述电磁特性的参数(ε、μ、σ)与空间坐标无关，则 是均匀媒质，否则是不均匀媒质； 2)若描述电磁特性的参数(ε、μ、σ)与场量（E或H）的大 小无关，则是线性媒质，否则是非线性媒质； 3)若描述电磁特性的参数(ε、μ、σ)与场量的方向无关， 则是各向同性媒质，否则是各向异性媒质。 对于线性（Linear）、均匀(Homogeneous)、各向同性 （Isotropic）媒质被称为L.H.I媒质。除非另外说明,这里 涉及的媒质是线性、均匀、各向同性媒质。 在真空（或空气）中，ε＝ε0，μ＝μ0，σ＝0。 理想介质指的是电导率σ＝0的情况； 理想导体是指电导率σ→∞的媒质。
H ( x, y,0, t ) ax H 0 sin ax cos(t ay)
求理想导体表面上的电流分布、电荷分布以及分 界面处的电场强度。 解：理想导体表面上的电流分布为
J s n H a z a x H 0 sin ax cos(t ay ) a y H 0 sin ax cos(t ay )
E d l 0
c
在时变场中应该修正以来代替，
那么恒定磁场的性质安培环路定律
B c E d l S t d S
H d l I
c
在时变场中是否也要修正呢？
全电流定律

全电流定律
D H J t

积分形式
D l H dl s ( J t ) ds
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
电磁场与电磁波
第4章 时变电磁场
1
本章内容
4.1 波动方程 4.2 电磁场的位函数 4.3 电磁能量守恒定理 4.4 惟一性定理 4.5 时谐电磁场
天津工业大学
电磁场与电磁波
第4章 时变电磁场
2
4.1 波动方程(Wave Equation)
问题的提出
麦克斯韦方程 —— 一阶矢量微分方程组，描述电场与磁场
天津工业大学
电磁场与电磁波
第4章 时变电磁场
12
电磁能量及守恒关系
电场能量密度：
we
1 2
ED
磁场能量密度：
wm
1 HB 2
dW
dt V
S
电磁能量密度：
w we wm
1 ED 1HB
2
2
空间区域V中的电磁能量：W wdV (1 E D 1 H B)dV
V
V2
2
特点：当场随时间变化时，空间各点的电磁场能量密度也要随
第4章 时变电磁场
10
2
A
2 A t 2
J
说明
2 2
t 2
应用洛仑兹条件的特点：① 位函数满足的方程在形式上是对称 的，且比较简单，易求解；② 解的物理意义非常清楚，明确地 反映出电磁场具有有限的传递速度；③ 矢量位只决定于J，标
量位只决定于ρ，这对求解方程特别有利。只需解出A，无需
解出 就可得到待求的电场和磁场。
S
dt V 2
2
V
其中： d (1 E D 1 H B) dV —— 单位时间内体积V 中所增加
dt V 2
2
的电磁能量
E J dV —— 单位时间内电场对体积V中的电流所作的功；
V
在导电媒质中，即为体积V内总的损耗功率
(E H) dS —— 通过曲面S 进入体积V 的电磁功率 S
天津工业大学
电磁位函数只是简化时变电磁场分析求解的一种辅助函数，应
用不同的规范条件，矢量位A和标量位 的解也不相同，但最终
得到的电磁场矢量是相同的。
问题 若应用库仑条件，位函数满足什么样的方程? 具有什么特点?
天津工业大学
电磁场与电磁波
第4章 时变电磁场
11
4.3 电磁能量守恒定律 讨论内容
电磁能量及守恒关系 坡印廷定理 坡印廷矢量
Ε 0
同理可得 问题
2E 2E 0
t 2
若为有源空间，结果如何？
若为导电媒质，结果如何？
H ( E )
t
( H )
2H
2H t 2
2H
2H t 2
0
天津工业大学
电磁场与电磁波
第4章 时变电磁场
4
4.2 电磁场的位函数
讨论内容
位函数的定义 位函数的性质 位函数的规范条件 位函数的微分方程
S
(E
H)
dS
d dt
V
(1 2
E
D
1 2
H
B) dV
V
E
J
dV
物理意义：单位时间内，通过曲面S 进入体积V的电磁能量等于 体积V 中所增加的电磁场能量与损耗的能量之和。
天津工业大学
电磁场与电磁波
第4章 时变电磁场
16
坡印廷矢量（电磁能流密度矢量）
描述时变电磁场中电磁能量传输的一个重要物理量
定义：S Ε H ( W/m2 )
时间改变，从而引起电磁能量流动
电磁能量守恒关系：
进入体积V的能量＝体积V内增加的能量＋体积V内损耗的能量
天津工业大学
电磁场与电磁波
第4章 时变电磁场
13
坡印廷定理
表征电磁能量守恒关系的定理
微分形式： (E H) (1 E D 1 H B) E J
t 2
2
积分形式： (E H) dS d (1 E D 1 H B) dV E J dV
电磁场与电磁波
第4章 时变电磁场
14
推证
H
J
D t
由
Ε
B t
Ε
H
Ε
J
Ε
D t
H
Ε
H
B t
将以上两式相减，得到
Ε H H Ε Ε J Ε D H B
t
t
当参数都不随时间变化时，则有
Ε D Ε Ε 1 (Ε Ε) (1 Ε D)
t
t 2 t
t 2
H B H H 1 (H H ) (1 H B)
天津工业大学
电磁场与电磁波
第4章 时变电磁场
5
引入位函数的意义 引入位函数来描述时变电磁场，使一些问题的分析得到简化。
位函数的定义
B 0
Ε B t
B A
(Ε A) 0 t
E A
t
天津工业大学
电磁场与电磁波
第4章 时变电磁场
6
位函数的不确定性
满足下列变换关系的两组位函数（A、）和（A、）能描述同
在电磁理论中，通常采用洛伦兹条件，即
A 0
t 除了利用洛伦兹条件外，另一种常用的是库仑条件，即
A 0
天津工业大学
电磁场与电磁波
第4章 时变电磁场
8
位函数的微分方程
DE H B
H J D t
B J E
t
B A E A
t
A J ( A )
t
t 2
t
t 2
天津工业大学
电磁场与电磁波
第4章 时变电磁场
15
再利用矢量恒等式： Ε H H Ε (Ε H )
即可得到坡印廷定理的微分形式
(Ε H ) (1 Ε D 1 H B) Ε J
t 2
2
在任意闭曲面S 所包围的体积V上，对上式两端积分，并应用散度 定理，即可得到坡印廷定理的积分形式
一个电磁场问题。
A
A
t
为任意可微函数
A (A ) A
即
A t
(
t
)
t
(
A
)
A t
也就是说，对一给定的电磁场可用不同的位函数来描述。不同位
函数之间的上述变换称为规范变换
原因：未规定 A的散度
天津工业大学
电磁场与电磁波
第4章 时变电磁场
7
位函数的规范条件
造成位函数的不确定性的原因就是没有规定 A 的散度。利用位 函数的不确定性，可通过规定 A 的散度使位函数满足的方程得以简 化。
间的相互作用关系
波动方程 —— 二阶矢量微分方程，揭示电磁场的波动性
麦克斯韦方程组
波动方程
无源区的波动方程
在无源空间中，设媒质是线形、各向同性且无损耗的均匀媒
质，则有
2E
ห้องสมุดไป่ตู้
2E t 2
0
2H
2H t 2
0
天津工业大学
电磁波动方程
电磁场与电磁波
第4章 时变电磁场
3
推证
H
Ε t
Ε
H t
H 0
E
物理意义：
S 的方向 —— 电磁能量传输的方向 S 的大小 —— 通过（垂直于能量传输方
t t A ( A) 2 A
2 A
2 A t 2
J
(
A
t
)
A 0
t
2 A 2 A J
t 2
天津工业大学
电磁场与电磁波
第4章 时变电磁场
9
同样
D
D E、E A
t
( A )
t
A 0
t
2 2
t 2
天津工业大学
电磁场与电磁波