第6章_磁介质

第六章 稳恒磁场思考题6-1 为什么不能把磁场作用于运动电荷的力的方向，定义为磁感强度的方向？答：对于给定的电流分布来说，它所激发的磁场分布是一定的，场中任一点的B 有确定的方向和确定的大小，与该点有无运动电荷通过无关。

而运动电荷在给定的磁场中某点 P 所受的磁力F ，无论就大小或方向而言，都与运动电荷有关。

当电荷以速度v 沿不同方向通过P 点时，v 的大小一般不等，方向一般说也要改变。

可见，如果用v 的方向来定义B 的方向，则B 的方向不确定，所以我们不能把作用于运动电荷的磁力方向定义为磁感应强度B 的方向。

6-2 从毕奥－萨伐尔定律能导出无限长直电流的磁场公式aIB πμ2=。

当考察点无限接近导线（0→a ）时，则∞→B ，这是没有物理意义的，如何解释？答：毕奥－萨伐尔定律是关于部分电流（电流元）产生部分电场（dB ）的公式，在考察点无限接近导线（0→a ）时，电流元的假设不再成立了，所以也不能应用由毕奥－萨伐尔定律推导得到的无限长直电流的磁场公式aIB πμ2=。

6-3 试比较点电荷的电场强度公式与毕奥－萨伐尔定律的类似与差别。

根据这两个公式加上场叠加原理就能解决任意的静电场和磁场的空间分布。

从这里，你能否体会到物理学中解决某些问题的基本思想与方法？答：库仑场强公式0204dqr dE rπε=，毕奥一萨伐定律0024Idl r dB r μπ⨯= 类似之处：（1）都是元场源产生场的公式。

一个是电荷元（或点电荷）的场强公式，一个是电流元的磁感应强度的公式。

（2）dE 和dB 大小都是与场源到场点的距离平方成反比。

（3）都是计算E 和B 的基本公式，与场强叠加原理联合使用，原则上可以求解任意分布的电荷的静电场与任意形状的稳恒电流的磁场。

不同之处： （1）库仑场强公式是直接从实验总结出来的。

毕奥一萨伐尔定律是从概括闭合电流磁场的实验数据间接得到的。

（2）电荷元的电场强度dE 的方向与r 方向一致或相反，而电流元的磁感应强度dB 的方向既不是Idl 方向，也不是r 的方向，而是垂直于dl 与r 组成的平面，由右手螺旋法则确定。

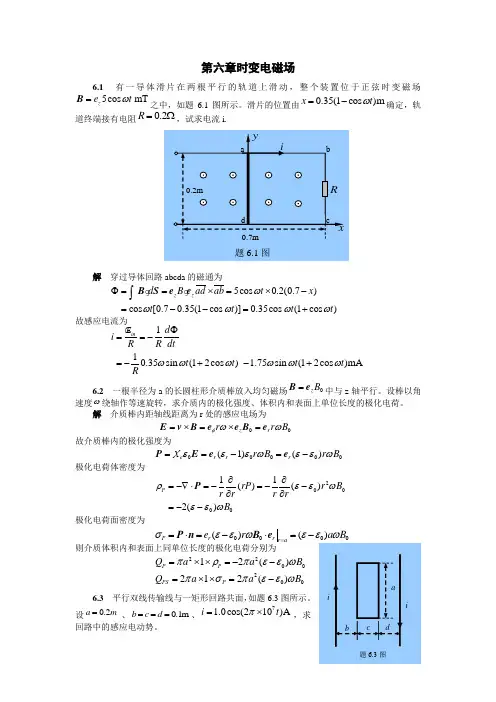
第六章时变电磁场6.1 有一导体滑片在两根平行的轨道上滑动，整个装置位于正弦时变磁场5cos mT z e t ω=B 之中，如题6.1图所示。

滑片的位置由0.35(1cos )m x t ω=-确定，轨道终端接有电阻0.2R =Ω，试求电流i.解 穿过导体回路abcda 的磁通为5cos 0.2(0.7)cos [0.70.35(1cos )]0.35cos (1cos )z z d B ad ab t x t t t t ωωωωωΦ==⨯=⨯-=--=+⎰ B S e e故感应电流为110.35sin (12cos ) 1.75sin (12cos )mAin d i R R dt t t t t R ωωωωωωΦ==-=-+-+E6.2 一根半径为a 的长圆柱形介质棒放入均匀磁场0z B =B e 中与z 轴平行。

设棒以角速度ω绕轴作等速旋转，求介质内的极化强度、体积内和表面上单位长度的极化电荷。

解 介质棒内距轴线距离为r 处的感应电场为 00z r r r B φωω=⨯=⨯=E v B e e B e故介质棒内的极化强度为 00000(1)()e r r r r B r B εεεωεεω==-=-P E e e X极化电荷体密度为2000011()()2()P rP r B r r r rB ρεεωεεω∂∂=-∇⋅=-=--∂∂=--P极化电荷面密度为00()()P r r r a e r a B σεεωεεω==⋅=-⋅=-P n B e 则介质体积内和表面上同单位长度的极化电荷分别为220020012()212()P P PS P Q a a B Q a a B πρπεεωπσπεεω=⨯⨯=--=⨯⨯=-6.3 平行双线传输线与一矩形回路共面，如题6.3图所示。

设0.2a m =、0.1m b c d ===、71.0cos(210)A i t π=⨯，求回路中的感应电动势。

第六章磁介质§2 等效的磁荷观点（P581）1.按照磁荷观点，§1习题1中的磁棒端面上磁荷密度和磁极强度为多少？解：2.一圆柱形永磁铁，直径 10毫米，长 100毫米，均匀磁化后磁极化强度J=1.20韦伯/米2，求：（1）它两端的磁极强度；（2）它的磁矩；（3）其中的磁场强度H和磁感应强度B。

此外，H和B 的方向有什么关系？[提示：利用表6-1给出的退磁因子。

]解：3.按磁荷观点重新计算§1习题3。

解：4. 按磁荷观点重新计算§1习题4。

解：5. （1）一圆磁片半径为R，厚度为l,片饿两面均匀分布着磁荷，面密度分别为σm和-σm（见附图）。

求轴线上离圆心为x处的磁场强度H。

（2）此磁片的磁偶极矩pm和磁矩m为多少？（3）试证明，当l<<R（磁片很薄）时，磁片外轴线上磁场分布与一个磁矩和半径相同的电流环所产生的磁场一样。

解：6.证明在真空中1高斯的磁感应强度相当于1奥斯特的磁场强度。

解：7. 地磁场可以近似地看做是位于地心的一个磁偶极子产生的，在地磁纬度45度处，地磁的水平分量平均为0.23奥斯特，地球的平均半径为 6370千米，求上述磁偶极子的磁矩。

解：8.地磁场可以近似的看做是位于地心的一个磁偶极子产生的，证明：磁倾角（地磁场的方向与当地水平面的之间的交角）i与地磁纬度ψ的关系为tani=2tanψ（见附图）。

解：9. 根据测量得出，地球的磁矩为8.4x1022安·米2。

（1）如果在地磁赤道上套一个铜环，在铜环中通以电流I，使它的磁矩等于地球的磁矩，求I的值（已知地球半径为 6370千米）；（2）如果这电流的磁矩正好与地磁矩的方向相反，问这样能不能抵消地球表面的磁场？解：10. 一磁铁棒长 5.0厘米，横截面积为 1.0厘米 2，设棒内所有铁原子的磁矩都沿棒长方向整齐排列，每个铁原子的磁矩为1.8x10-23安·米2。

（1）求这磁铁棒的磁矩m和磁偶极矩pm；（2）当这磁铁棒在B=1.5高斯的外磁场中，并与B垂直时，B使它转动的力矩有多大？解：11.一磁针的磁矩为20安·米2，处在B=5.0x10-2高斯的均匀外磁场中。

1第6章 稳恒电流的磁场一 基本要求1. 掌握磁感应强度B的概念。

2. 掌握毕奥－萨伐尔定律，并能用该定律计算一些简单问题中的磁感应强度。

3. 掌握用安培环路定律计算磁感应强度的条件及方法，并能熟练应用。

4. 理解磁场高斯定理。

5. 了解运动电荷的磁场。

6. 理解安培定律，能用安培定律计算简单几何形状的载流导体所受到的磁场力。

7. 理解磁矩的概念，能计算平面载流线圈在均匀磁场中所受到的磁力矩，了解磁力矩所作的功。

8. 理解并能运用洛伦兹力公式分析点电荷在均匀磁场（包括纯电场、纯磁场）中的受力和运动的简单情况。

9. 了解霍耳效应。

10. 了解磁化现象及其微观解释。

11. 了解磁介质的高斯定理和安培环路定理，能用安培环路定理处理较简单的介质中的磁场问题。

12. 了解各向同性介质中H 与B的联系与区别。

13. 了解铁磁质的特性。

二 内容提要1. 毕奥－萨伐尔定律 电流元Id l 在真空中某一场点产生的磁感应强度d B 的大小与电流元的大小、电流元到该点的位矢r与电流元的夹角θ的正弦的乘积成正比，与位矢大小的平方成反比，即204r l I B θπμsin d d =dB 的方向与r l I⨯d 相同，其矢量式为304r rl I B⨯=d d πμ 2. 几种载流导体的磁场 利用毕奥－萨伐尔定律可以导出几种载流导体磁场的分布，这些结果均可作公式应用。

（1）有限长直载流导线的磁感应强度的大小)cos (cos π2104θθμ-=aIB方向与电流成右手螺旋关系。

式中，a 为场点到载流直导线的距离，21θθ、分别为直导线始末两端到场点的连线与电场方向的夹角。

2（2）长载流直导线（无限长载流直导线）的磁感应强度的大小rIB πμ20=方向与电流成右手螺旋关系。

（3） 直载流导线延长线上的的磁感应强度 0=B（4） 载流圆导线（圆电流）轴线上的磁感应强度的大小2322202)(x R IR B +μ=方向沿轴线，与电流成右手螺旋关系。

第6章 恒定磁场一、目的与要求1．掌握磁感应强度的概念和毕奥—萨伐尔定律，能用毕奥—萨伐尔定律和磁场叠加原理熟练求解简单情况下电流的磁场分布。

2．掌握磁通量的概念，磁场的高斯定理及安培环路定理，会计算给定面的磁通量，并能利用安培环路定理求解具有对称性的电流的磁场分布。

3．掌握磁场对载流导线的作用和对平面载流线圈的作用力矩，会计算磁力的功；能分析和计算电荷在正交的均匀电磁场中的受力和运动情况；了解霍尔效应。

4．理解磁介质的磁化机理，掌握有磁介质时的安培环路定理及其应用。

二、内容提要1．描述磁场的物理量——磁感应强度 （1）磁感应强度的概念 磁感应强度B 的大小：lI F B d d max=磁感应强度B 的方向：电流元l d I 受力为零时l d I 的所在方向，且满足关系B l F ⨯=d d I（2）毕奥——萨伐尔定律 30d π4d r I rl B ⨯=μ（3）运动电荷的磁场30π4r q r B ⨯=v μ2．磁通量⎰⋅=ΦSm S B d3．描述磁场性质的两个定理 （1）磁场的高斯定理： 0d =⋅⎰SS B（2）安培环路定理： ∑⎰=⋅)(0d 内i L I μl B 4．磁场对电流的作用 （1）磁场对载流导线的作用力B l F ⎰⨯=LI d（2）均匀磁场对刚性平面载流线圈的作用线圈所受的合力∑=0F线圈所受的力矩B P M ⨯=m 其中n P IS m =，为载流线圈的磁矩。

5．磁力的功若载流导线或线圈中有恒定电流I 时，均匀磁场对载流导线或载流线圈所作的功均可表示为m I A ∆Φ=其中m ∆Φ通过载流线圈的磁通量的增量。

6．磁场对运动电荷的作用力B f ⨯=v q7．霍尔效应：在磁场中载流导线上出现横向电势差的现象。

横向电势差为dd IBk nq IB u ab ==8．物质的磁化（1）磁介质的分类：顺磁质，抗磁质，铁磁质。

（2）磁介质中的安培环路定理：∑⎰=⋅ii LI)(d 0内l H（3）铁磁质有磁滞现象。

第六章稳恒磁场
1、主要的概念：电流强度，磁感应强度，电流元，磁感应线，磁通量，磁化和磁介质。

2、主要的了解定律：磁场叠加原理，毕奥—萨伐尔定律（推导一些特殊载流导线和运动电荷的B），磁场中的高斯定律，安培环路定律。

（了解定理的导出以及其重要的物理意义）
3、主要计算：利用毕奥—萨伐尔定律、安培环路定理计算一些特殊载流导线产生的磁感应强度；安培力和洛伦兹力的计算；磁介质中的磁化，以及应用介质中的安培环路定理计算磁场强度矢量（H）和磁感应强度（B）。

4、重点内容：毕奥—萨伐尔定律、安培环路定理、磁场力、力矩；磁介质的磁化、介质中的安培环路定理。

2．磁场方程： 磁场高斯定理：
（表明磁场是无源场）
（表明磁场是有旋场）
掌握推导过程
*通过霍尔电压可以求得磁场和电流大小。

6. 均匀磁化的B 、H 、M 关系及表面磁化电流密度与磁化强度的关系
）
（M H B 0 +=μ H M m χ= m r 1χμ+=
B 代表 H 代表 M 代表
—
——m r 0χμμ 4.载流线圈的磁矩 3.电磁相互作用 B
l Id f d ⨯=2)磁场对载流导线的安培力
⎰⨯=l
B
l Id f 3)磁场对载流线圈的作用力矩 B
m M
⨯=4)5.霍耳电压
1)安培定律。

§6 磁介质 ( Magnetic medium)§6－1 分子电流观点1. 何为磁介质在前几章里讨论载流线圈产生磁场和变化的磁场产生感应电动势的时候，都假定导体以外是真空，或者不存在磁性物质（磁介质）。

然而在实际中大多数情况下电感器件（如镇流器、变压器、电动机和发电机）的线圈中都有铁芯。

那么，铁芯在这里起什么作用呢？为了说明这个问题，看一个演示实验。

图6-2就是有关电磁感应现象的演示实验，当初级线圈的电路中开关K 接通或断开时，就在次级线圈A 中产生一定的感应电流。

不过这里我们在线圈中加一软铁芯。

重复上述实验就会发现，次级线 圈中的感应电流大大增强了。

知道 感应电流的强度是与磁通量的时间变化率成正比的。

上述实验表明，铁芯可以使线圈中的磁通量大大增加。

2.两种观点图6-1居里夫人图6-2电磁感应现象的演示实验有关磁介质（铁芯）磁化的理论，有两种不同的观点—— 分子电流观点和磁荷观点。

两种观点假设的微观模型不同，从而赋予磁感应强度B 和磁场强度H 的物理意义也不同，但是最后得到的宏观规律的表达式完全一样，因而计算的结果也完全一样。

在这种意义下两种观点是等效的。

本节介绍分子电流观点，下节介绍磁荷观点，并讨论两种观点的等效性问题。

3. 分子电流观点分子电流观点即安培的分子环流假说。

现在按照这个观点来说明，为什么铁芯能够使线圈中的磁通量增加。

如图6-3，我们考虑一段插在线圈内的软铁棒。

按照安培分子环流的观点，棒内每个磁分子相当于一个环形电流。

在没有外磁场的作用下，各 分子环流的取向是杂乱无章的（图6-3)，它们的磁矩相互抵消。

宏观看起来，软铁棒不显示磁性。

我们说，这时它处于未磁化状态。

当线圈中通人电流后，它产生一个外磁场B （这个由外加电流产生，并与之成正比的磁场，又叫做磁化场，产生磁化场的外加电流，叫做励磁电流）。

在磁化场的力矩作用下，各分子环流的磁矩在一定程度 上沿着场的方向排列起来（图6-4)。

第六章磁介质§3 介质的磁化规律（P605）1. 一环形铁芯横截面的直径为 4.0毫米 ,环的平均半径R= 15毫米 ,环上密绕着200匝线圈(见附图),当线圈导线通有25毫安的电流时,铁芯的(相对)磁导率μ=300,求通过铁芯横截面的磁通量Φ。

解：2.一铁环中心线的周长为 30厘米，横截面积为 1.0厘米 2，在环上紧密地绕有300匝表面绝缘的导线。

当导线中通有电流32毫安时，通过环的横截面的磁通量为2.0x10-6韦伯。

求：(1)铁环内部磁感强度的大小B；(2)铁环内部磁场强度的大小H；（3）铁的磁化率Χm和（相对）磁导率μ（4）铁环的磁化强度的大小M。

解：3.一螺绕环由表面绝缘的导线在铁环上密绕而成,每厘米绕有10匝;当导线中的电流为2.0安时,测得铁环内的磁感强度为1.0特斯拉。

求：（1）铁环内的磁场强度H；（2）铁环的磁极化强度J；（3）铁环的（相对）磁导率μ。

解：4.一无穷长圆柱形直导线外包一层磁导率为μ的圆筒形磁介质，导线半径为R1，磁介质的外半径为R2（见附图），导线内有电流I通过。

（1）求介质内，外的磁场强度和磁感应强度的分布，并画H-r，B-r曲线；（2）介质内，外表面的磁化面电流密度i’；（3）从磁荷观点来看，介质表面有无磁荷？解：5. 若§1习题6磁介质的磁导率μ=200，B=2.0特斯拉，求两空穴中心的H。

解：6. 一抗磁质小球的质量为 0.10克。

密度为ρ= 9.8克 /厘米3，磁化率为Χm=-1.82x10-4。

放在一个半径R= 10厘米的圆线圈的轴线上距圆心为l= 10厘米处（见附图）。

圈中载有电流I=100安。

求电流作用在这抗磁质小球上力的大小和方向。

[提示：参看§2习题13。

]解：7.附图是某种铁磁材料的起始磁化曲线，试根据这曲线求出最大磁导率μM，并绘制响应的μ-H曲线。

解：8. 附表中列出某种磁性材料的H和B的实验数据，（1）画出这种材料的起始磁化曲线；（2）求出表中所列出的各点处材料的（相对）磁导率μ；（3）求最大磁导率μM。