2000年东北大学信号与系统考研试题

东北大学通信信号考研经验东北大学2012 通信与信息系统复试线332，统招27人，32人达复试线，31 人参加复试，1 人调剂；2011 复试线375，统招17 人，每年排名后13 名的第二年需要去秦皇岛。

我考研只花了5-6 个月的时间，所以，只要你能坚持下来，就能成功，东大还是相当公平的，对普通的学校没有歧视，面试拉不开分。

通信与信息系统、信号与信息处理、电子与通信工程初试都考信号与系统，考的很简单，参考书目是郑君里的第二版信号与系统，严格按照考试大纲复习，大纲上没有的肯定不考，课后习题一定多做，有的比较难的就别做了，信号考的还是比较简单，反复做真题、课后习题，有时间还可以做做吴大正的课后习题，2012就考到一道原题，15分，S域变化中的电路模型必须记住，一般考的是串联型的，含受控源的电路也要掌握，2012就考到一题。

总之，做熟真题、课后习题，就OK！通信与信息系统、电子与通信工程，复试都考通信原理（国防工业第六版樊昌信）和高频电子线路（张肃文第三版）,电路与系统可选考通原和高频。

通信原理有个大纲，是按照第五版教材编写的，通原的课后习题和真题一定得做透，2012考了四道大题，每题15分，全是计算题；高频考的几乎都是简答题，2012考了7道题，有2道计算，主要是背笔记和06-07的题，我这试卷题前的页码是对应答案的页码。

2012和2011考的很多都一样，所以，2012和2011的题大家一定得把背下来。

2012东北大学通信与信息系统复试面试回忆东北大学信息学院听说只有双控有英语听力，据说是用笔记本放的，其余专业貌似对英语要求不严，自我介绍都直接用中文，不过具体情况大家需要自己去了解。

通信2011、2012面试自我介绍都用的是中文，不过还是建议大家准备份英文介绍背熟，可能明年就变了呢。

面试时是五个老师，分2组，分别是雷为民和沙毅老师主持，一般按排名先后进去，上午全部可以结束。

进去了首先是中文自我介绍，然后问了以下几个问题：1、信源编码与信道编码的区别；2、电视线为什么比电话线粗？（PS：电视线用的是同轴电缆，电话线是普通的平行导线，大家可以想到香农公式，答案就是：同轴电缆噪声小，带宽大）；3、二进制文件与文本文件的区别？（PS：我说自己编过一千多行的程序，老师就问我这个问题了）；4、信号与系统的区别？（PS：老师问我除了初试复试考的课外，什么课学的比较好，因为我是电子专业的，说的课程都与通信没什么关系，老师就说问我信号与系统吧）；5、英文测试就问了我三个通信相关的简称，我只答对了一个，CDMA，其余的没听过，也就不知道了；6、同步通信与异步通信的区别？7、TCP/IP协议有哪四层？8、结构体与共用体的区别？8、除了初试和复试考的专业课，你认为哪些你学的比较好？差不多就这些问题，还有几个记不得了，最后还问我大学阶段有没当过学生干部，是不是党员，主考官还问下了后面的老师我的成绩怎么样，他好打分。

2000年武汉大学信号与系统参考答案一、 答：1.由图（1-a ）可得：1213e()[()()()()]()t h t h t h t h t y t *+**= 故系统的冲激响应：1213()()()()()()(1)()(())()(1)h t h t h t h t h t u t t u t t t u t u t δδ=+**=+-**-=-- 2. 根据卷积积分性质：1212()()()()df t f t f t f d dtττ*=*⎰ 故当输入的激励信号如图（1-b ）所示时，系统的零状态响应为：222222()()()()()11[()(1)]{[()(0.1)](0.2)[(0.1)(0.2)]}505011[()(0.1)](0.2)[(0.1)(0.2)]505011(1)[(1)( 1.1)]( 1.2)[( 1.1)5050zs y t e t h t dh t e d dtt t t u t u t t u t u t t u t u t t u t u t t u t u t t u t ττδδ=*=*=--*-------=------------+--⎰( 1.2)]u t -- 画图略二、答：1.记11()()h t H j ω⇔，则010100002()()()()()()()()()()mm mf t f t h t F j F j H j f t Sa t F j G ωωωωωωωωωπω=*⇔=•=⇒=0()F j ω如下图示：w因此由01()()()F j F j H j ωωω=•，以及图（2-b ），可得()F j ω：2.由上面分析知道，信号()f t 的最大频率为m ω，根据奈奎斯特采样定理，要使()s f t 包含()f t 的全部信息，则()T t δ得T 应满足：22m mT ππωω≤=，即()T t δ的最大时间间隔为：max mT πω=。

2000年一、选择题（每小题3分，共30分）1、已知y (t )=x (t )*h (t )，g (t )=x (3t )*h (3t )，x (t )↔X (j ω)，h (t )↔H (j ω)，则g (t ) = ( )。

（a ）⎪⎭⎫ ⎝⎛33t y（b ）⎪⎭⎫ ⎝⎛331t y （c ）()t y 331（d ）()t y 3912、差分方程)()2()5()3(6)(k f k f k y k y k y --=+++-所描述的系统是（ ）的线性时不变系统。

（a ）五阶 （b ）六阶 （c ）三阶 （d ）八阶3、已知信号f 1(t )，f 2(t )的频带宽度分别为∆ω1和∆ω2，且∆ω2>∆ω1，则信号y (t )= f 1(t )*f 2(t )的不失真采样间隔（奈奎斯特间隔）T 等于（ ）。

（a ）21πωω∆+∆（b ）12πωω∆-∆（c ）2πω∆ （d ）1πω∆ 4、已知f (t )↔F (j ω)，则信号y (t )= f (t )δ (t -2)的频谱函数Y (j ω)=（ ）。

（a ）ωω2j e)j (F（b ）ω2-j e)2(f（c ）)2(f （d ）ω2j e)2(f5、已知一线性时不变系统的系统函数为)2)(1(1-)(-+=s s s s H ，若系统是因果的，则系统函数H (s )的收敛域ROC 应为（ ）。

（a ）2]Re[>s（b ）1]Re[-<s（c ）2]Re[<s （d ）2]Re[1<<-s6、某线性时不变系统的频率特性为ωωωj j )j (-+=a a H ，其中a >0，则此系统的幅频特性|H (j ω)|=（ ）。

（a ）21（b ）1（c ）⎪⎭⎫⎝⎛-a ω1tan （d ）⎪⎭⎫ ⎝⎛-a ω1tan 2 7、已知输入信号x (n )是N 点有限长序列，线性时不变系统的单位函数响应h (n )是M 点有限长序列，且M >N ，则系统输出信号为y (n )= x (n )*h (n )是（ ）点有限长序列。

武汉大学2000年信号与系统试题 参考答案一、 答：1.由图（1-a ）可得：1213e()[()()()()]()t h t h t h t h t y t *+**= 故系统的冲激响应：1213()()()()()()(1)()(())()(1)h t h t h t h t h t u t t u t t t u t u t δδ=+**=+-**-=-- 2. 根据卷积积分性质：1212()()()()df t f t f t f d dtττ*=*⎰ 故当输入的激励信号如图（1-b ）所示时，系统的零状态响应为：222222()()()()()11[()(1)]{[()(0.1)](0.2)[(0.1)(0.2)]}505011[()(0.1)](0.2)[(0.1)(0.2)]505011(1)[(1)( 1.1)]( 1.2)[( 1.1)5050zs y t e t h t dh t e d dtt t t u t u t t u t u t t u t u t t u t u t t u t u t t u t ττδδ=*=*=--*-------=------------+--⎰( 1.2)]u t -- 画图略二、答：1.记11()()h t H j ω⇔，则010100002()()()()()()()()()()mm mf t f t h t F j F j H j f t Sa t F j G ωωωωωωωωωπω=*⇔=•=⇒=0()F j ω如下图示：w因此由01()()()F j F j H j ωωω=•，以及图（2-b ），可得()F j ω：2.由上面分析知道，信号()f t 的最大频率为m ω，根据奈奎斯特采样定理，要使()s f t 包含()f t 的全部信息，则()T t δ得T 应满足：22m mT ππωω≤=，即()T t δ的最大时间间隔为：max mT πω=。

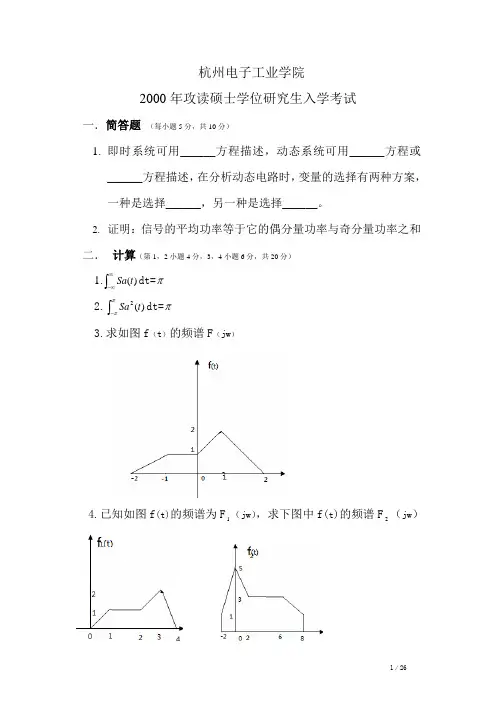
杭州电子工业学院
2000年攻读硕士学位研究生入学考试
一．简答题（每小题5分，共10分）
1.即时系统可用______方程描述，动态系统可用______方程或
______方程描述，在分析动态电路时，变量的选择有两种方案，一种是选择______，另一种是选择______。

2.证明：信号的平均功率等于它的偶分量功率与奇分量功率之和二． 计算（第1，2小题4分，3，4小题6分，共20分）
1.dt=
∫∞∞−)(t
Saπ
2.dt=
∫−ππ)(2t
Saπ
3.求如图f（t）的频谱F（jw）
4.已知如图f(t)的频谱为F（jw），求下图中f(t)的频谱F（jw）
12
三．（12分）如图所示系统，h =a δ（t -1） h =b δ（t）+δ（t-2）， h =u （t）-（t-2） h =u （t）-u （t-3）当激励为e （t）=u （t）-u （t-2），求系统的的零状态响应r（t）
c
d
四．（8分）已知某线性时不变系统当激励为e （t）= 2sint u（t）时零状态响应r（t）为如图波形，求系统冲激响应
h（t）的波形。

五．（8分）系统如图所示，试画出其流图表示，并求转移函数H（s）=)
()(s X s Y。

六．（10分）信号的频谱如图所示，若此信号通过下图系统，试绘出
A、B、C、D 各点信号的频谱图形，设理想滤波器截止频率均为W ，。