第3章网络分析方法和网络定理
- 格式:ppt
- 大小:1.93 MB
- 文档页数:39

电路基础-陈佳新-第3章电路的分析计算法之二——电路方程法引言在电路分析中,电路方程法是一种重要且常用的方法。
通过建立和求解电路方程,可以得到电路中各个元件的电压、电流以及功率等信息。
在本文中,将介绍电路方程法的基本概念、原理和应用。
电路方程法的基本概念电路方程法是通过建立和求解电路方程来分析电路的一种方法。
对于一个电路,可以通过网络定理(如基尔霍夫定律)和元件特性等,建立一组与电压和电流相关的方程。
通过求解这组方程,可以得到电路中各个元件的电压、电流以及功率等。
电路方程的建立建立电路方程的关键是根据电路的拓扑结构和元件特性,利用基尔霍夫定律和欧姆定律等,建立与电压和电流相关的方程。
基尔霍夫定律基尔霍夫定律是分析电路的基本定律之一,分为基尔霍夫电流定律和基尔霍夫电压定律。
基尔霍夫电流定律基尔霍夫电流定律是指在一个节点处,电流进入节点的总和等于电流离开节点的总和。
根据该定律,可以得到关于电路中电流的方程。
基尔霍夫电压定律基尔霍夫电压定律是指在电路中的任意一个回路中,电压升降之和等于零。
根据该定律,可以得到关于电路中电压的方程。
元件特性和欧姆定律电路中的元件具有一定的特性,如电阻、电感和电容的特性。
其中,电阻是电流和电压之间的线性关系,电感是电流和电压之间的积分关系,电容是电流和电压之间的微分关系。
利用这些特性和欧姆定律,可以得到与电路中各个元件相关的方程。
电路方程的求解建立了电路方程之后,需要求解这些方程,得到电路中各个元件的电压、电流以及功率等信息。
构建方程组根据电路的拓扑结构和元件特性,可以得到一组关于电压和电流的方程。
将这些方程整理成一个方程组,可以利用代数或数值方法求解。
代数方法对于一些简单的线性电路,可以利用代数方法求解方程组。
通过代数运算,可以得到方程组的解析解,即电路中各个元件的电压、电流以及功率等。
数值方法对于一些复杂的非线性电路或无法通过代数方法求解的电路,可以利用数值方法求解方程组。
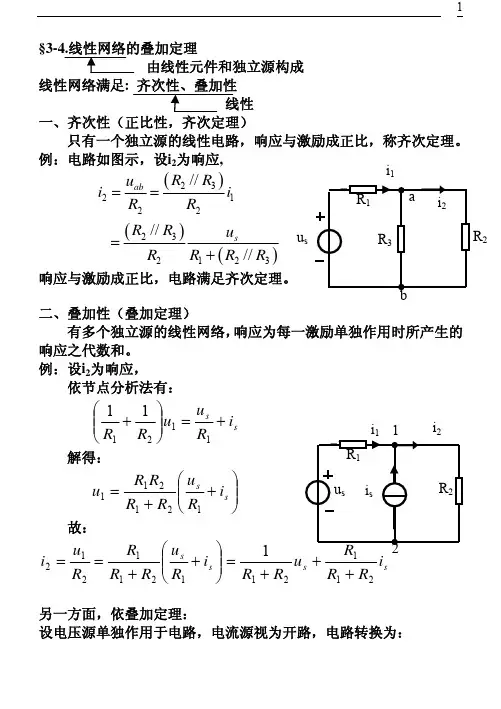
只有一个独立源的线性电路,响应与激励成正比,称齐次定理。
例:电路如图示,设i 2为响应,()()()232122232123//// //ab sR R u i i R R R R u R R R R ===+二、叠加性(叠加定理) 有多个独立源的线性网络,响应为每一激励单独作用时所产生的响应之代数和。
例:设i 2为响应,依节点分析法有:21211212⎠⎝i 2=另一方面,依叠加定理:设电压源单独作用于电路,电流源视为开路,电路转换为:2112R R u i s+=−s i R R R i 21122+=−依叠加定理,当两个独立源同时作用于电路时,有:12212212121s s R i i i u i R R R R −−=+=+++与节点电位分析法求得的结论一致。
注:在使用叠加定理时,应注意以下几点:1) 线性电容()视为端电压随时间变化的理想电压源;c q u ∝线性电感(L i ψ∝)视为端电流随时间变化的理想电流源。
2)当某一激励源单独作用时,其它激励源视为零值(电压源视为短路;电流源视为开路)。
3)受控源不能视为激励。
4)叠加定理不适合功率计算(非线性 22Ri RuP ==∵)。
5)多个激励时,只有当所有激励都扩大k 倍时,响应才扩大k 倍。
例3-17用叠加定理求图中电压U 1及电流源的功率解:设电压源单独作用,电流源视为开路,电路为右图所示:依分压公式有: V U 102510//201010//2011=×+=−设电流源单独作用,电压源视为短路,电路为下图所示:()V U 65.110//10//2021=×=−设电压源和电流源同时作用:V U U U 1661021111=+=+=−−电流源的端电压:V U U 91625251=−=−=电流源吸收的功率(注意:电流源为关联参考方向):9 1.513.5P U I W =×=×=例3-18用叠加定理求I x解:设电压源单独作用(受控源不能单独作用),电路如右图所示:()AI I I X X X 2010212 111=∴=−++−−−设电流源单独作用,电路为右图示:用节点分析法,有:⎪⎩⎪⎨⎧−=+=⎟⎠⎞⎜⎝⎛+−−补充212311212121X X I U I U解得:A I X 6.02−=−()A I I I X X X 4.16.0221=−+=+=−−例3-19设,利用响应与激励成比例的性质求:V U S 4−=?=IIA I 1=V U S 36=,由图可推得:解:设依齐次定理:S S S U I U I k kU I 361361=⇒==⇒=依题意: ()A I V U S 9143614−=−=⇒−=作业:3-14,3-17。




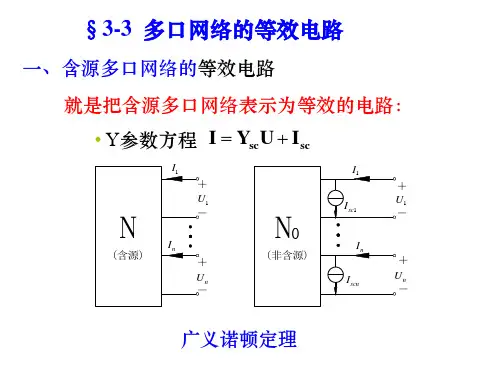



⽹络分析法⽹络分析法(Analysis Network Process Method)简介1996年Saaty教授在层次分析法(AHP)的基础上提出了⽹络分析法(Analysis Network Process Method ,ANP)。
ANP⽅法的基本理论与AHP 法相同,不同的是模型结构,ANP 法中引⼊超矩阵的概念,采⽤这种⽅法,所有⽹络结构中的元素均能够对结论产⽣影响,最终结果不仅被备选⽅案的权重影响,也被备选⽅案所属元素集影响,可以通过反馈更好的反映现实⽣活。
ANP法的基本结构与AHP法⾃上⽽下的层次结构不同,ANP法的⽹络结构中的连接没有固定⽅向,它既包括元素集之间的循环连接,也包括元素集对⾃⾝的反馈连接,这种⽹络结构往往能够较好的反映现实社会的问题,并且采⽤这种将问题细化结构、简单计算的⽅法远⽐采⽤简单划分结构、复杂计算过程的⽅法得到结果更令⼈满意。
⽹络分析法模型将系统分为控制层和⽹络层两个部分,控制层包括决策问题的⽬标和决策准则,⾄少应存在⼀个⽬标,但决策的准则可以没有,⽹络层由元素组组成,这些元素组受到控制层的⽀配,元素组间以及内部元素之间相互依存、相互影响,形成了⽹络结构。
典型的ANP模型如图所⽰:⽹络分析法的基本步骤:1)分析问题对决策问题进⾏分析,形成元素集,分析元素层次是否内部独⽴,是否存在依存和反馈,分析⽅法类同于AHP⽅法,可采⽤会议法、专家填表等形式进⾏。
2)构造ANP的典型结构⾸先构造控制层,界定决策⽬标和准则,再构造⽹络层次,分析每⼀个元素集的⽹络结构和相互影响关系,元素集间关系确定后即可构建相应的ANP⽹络,基本实际问题中都是既有内部依存⼜有循环的ANP⽹络层次。
3)构造ANP的超矩阵计算权重⽹络分析法中的1-9标度法⼏种常⽤的多⽬标决策⽅法VAGUE ⽅法Vague ⽅法由Cau 和Buehrer 提出,其本质是模糊集理论的⼀种推⼴形式。
Vague 集由真、假⾪属函数定义,体现了元素对模糊概念的属于与不属于程度,较传统的模糊集理论有更强的表达不确定性的能⼒,且更具灵活性。
线性电路的分析方法和网络定理
线性电路的分析方法主要有两种:基尔霍夫定律分析法和等效电路法。
1. 基尔霍夫定律分析法:
基尔霍夫定律是指基尔霍夫电流定律和基尔霍夫电压定律。
根据基尔霍夫电流定律,一个节点的进入电流等于离开电流的代数和。
根据基尔霍夫电压定律,一个回路中所有电压的代数和等于零。
利用这两个定律,可以列出若干个方程来求解电路的未知量,比如电流和电压。
2. 等效电路法:
等效电路法是指通过将复杂的线性电路简化为等效电路,再进行分析。
常见的等效电路包括电阻、电容和电感等。
通过将电路中的各个元件用等效电路替代,可以用简单的电阻、电容和电感的连接方式来分析电路。
等效电路法可以大大简化复杂的电路分析过程,使得计算更加方便。
网络定理是一种用于分析线性电路的重要工具,常见的网络定理包括:欧姆定律、基尔霍夫定律、奥姆-柯西定律、叠加原理、原电流原压理论、特尔肯定理等。
这些定理可以用来简化电路分析过程,提高分析的效率和准确性。
例如,奥姆定律可以通过电压和电阻的关系来计算电流;叠加原理可以将复杂电路分解为几个简单电路进行分析;特尔肯定理可以通过等效电路简化电路分析等。
第三章线性网络的一般分析方法和网络定理线性网络的一般分析方法和网络定理是线性系统理论的基础,对于理解和分析线性网络的性质和行为具有重要意义。
本章将介绍线性系统的一般分析方法和一些常见的网络定理。
线性网络一般分析方法包括模型描述、稳态分析和频域分析等。
模型描述是指将线性系统用数学方程建模,常见的描述方法包括微分方程、差分方程和传递函数等。
稳态分析是指研究系统在长时间作用下的稳定行为,包括零输入响应和零状态响应。
频域分析是指将系统的输入和输出用频域表达,通过频率响应函数分析系统的频率特性。
线性系统的性质和行为可以利用一些重要的网络定理进行分析和描述。
常见的网络定理包括叠加原理、超级位置原理、频域定理和稳定性条件等。
叠加原理是线性系统最基本的性质之一,它表示系统输出可以分解为各个输入分量响应的叠加。
具体地说,如果一个线性系统对于输入信号x1(t)的响应为y1(t),对于输入信号x2(t)的响应为y2(t),那么对于输入信号x(t)=x1(t)+x2(t),系统的响应为y(t)=y1(t)+y2(t)。
超级位置原理是叠加原理的一种推广,它描述了线性系统对于输入信号的定比例缩放响应的性质。
具体地说,如果一个线性系统对于输入信号x(t)的响应为y(t),那么对于输入信号kx(t)(k为常数),系统的响应为ky(t)。
频域定理是指在频域上分析线性系统的性质和行为,常见的频域定理包括傅里叶变换、拉普拉斯变换和z变换等。
通过频域分析,可以得到系统的频率响应函数,从而研究系统的频率特性。
稳定性条件是指线性系统的稳定性的必要和充分条件。
对于连续时间系统,稳定性条件是系统的所有特征根(极点)的实部都小于零;对于离散时间系统,稳定性条件是系统的所有特征根(极点)的模都小于1除了以上介绍的常见网络定理外,还有一些其他重要的网络定理,如包络定理、发散定理、主值定理等,它们在具体的分析和设计问题中具有重要的应用。
总之,线性网络的一般分析方法和网络定理是理解和分析线性系统行为和性质的基础。
第 3 章电路的一般分析方法与常用定理重点1.KCL和KVL独立方程数的概念;2.支路法、网孔法、节点法等复杂电路的方程法;3.叠加定理;4.戴维宁定理和诺顿定理;5.最大功率传输定理。
难点1.独立回路的确定;2.含独立电源的结点电压方程和回路电流方程的列写;3.各电路定理的应用条件;4、正确作出戴维南定理的等效电路。
3.1 支路电流法电路的一般分析方法是指在给定电路结构和元件参数的条件下,不需要改变电路结构,而是通过选择电路变量(未知量),根据KCL 和KVL 以及支路的VCR 建立关于电路变量的方程组,从而求解电路的方法。
一、支路电流法支路电流法是以支路电流为未知量,根据KCL建立独立节点电流方程,根据KVL 建立独立回路电压方程,然后解联立方程组求出各支路电流。
上图中选定各支路电流参考方向,并设各支路电压与支路电流为关联参考方向。
根据KCL 列出的节点电流方程分别为在上图所示的平面电路中含有3个网孔,若选择网孔作为回路,并取顺时针为回路绕行方向,根据KVL 列出含VCR 的回路电压方程分别为上面这3个回路电压方程也是相互独立的,对应于独立方程的回路称为独立回路。
由此可见,上图所示的电路共设有6条支路电流为未知量,分别列出了3个独立节点电流方程和3个独立回路电压方程,恰好等于6条未知的支路电流数,因此可以解出各支路电流。
二、支路电流法的应用应用支路电流法分析电路的关键在于确定独立节点和独立回路。
可以证明,对于具有n 个节点,b 条支路的电路,其独立节点数为(n -1 ) ,独立回路数为L = b -(n -1)。
对于平面电路,由于网孔数等于独立回路数, 综上所述,应用支路电流法求解电路的一般步骤是:(1) 选定支路电流的参考方向,确定独立节点、独立回路及其绕行方向。
(2)根据 KCL 列出(n-1)个独立节点电流方程。
(3)根据 KVL 列出L = b-(n-1)个独立回路电压方程。
(4)解方程组求出各支路电流。