【文库精品】高中数学 第二章 2.2.3 直线与平面平行的性质练习 新人教A版必修2

2021年高中数学 2.3直线、平面平行的性质与判定练习新人教A版必修21．下列命题中正确的个数是( )①若直线a不在α内，则a∥α；②若直线l上有无数个点不在平面α内，则l∥α；③若直线l与平面α平行，则l与α内的任意一条直线都平行；④如果两条平行线中的一条与一个平面平行，那么另一条也与这个平面平行；⑤若l与平面α平行，则l与α内任何一条直线都没有公共点；⑥平行于同一平面的两直线可以相交．A．1 B．2C．3 D．4答案B解析a∩α＝A时，a不在α内，∴①错；直线l与α相交时，l上有无数个点不在α内，故②错；l∥α时，α内的直线与l 平行或异面，故③错；a ∥b ，b ∥α时，a ∥α或a ⊂α，故④错；l ∥α，则l 与α无公共点，∴l 与α内任何一条直线都无公共点，⑤正确；如图，长方体中，A 1C 1与B 1D 1都与平面ABCD 平行，∴⑥正确．2．给出下列关于互不相同的直线l 、m 、n 和平面α、β、γ的三个命题： ①若l 与m 为异面直线，l ⊂α，m ⊂β，则α∥β；②若α∥β，l ⊂α，m ⊂β，则l ∥m ；③若α∩β＝l ，β∩γ＝m ，γ∩α＝n ，l ∥γ，则m ∥n . 其中真命题的个数为( ) A ．3 B ．2 C ．1 D ．0答案 C解析 ①中当α与β不平行时，也能存在符合题意的l 、m . ②中l 与m 也可能异面．③中⎭⎪⎬⎪⎫l ∥γl ⊂ββ∩γ＝m ⇒l ∥m ， 同理l ∥n ，则m ∥n ，正确． 3．下列命题中，是假命题的是( )A ．三角形的两条边平行于一个平面，则第三边也平行于这个平面B ．平面α∥平面β，a ⊂α，过β内的一点B 有唯一的一条直线b ，使b ∥aC ．α∥β，γ∥δ，α、β分别与γ、δ的交线为a 、b 、c 、d ，则a ∥b ∥c ∥dD ．一条直线与两个平面成等角是这两个平面平行的充要条件 答案 D解析 D 错误．当两个平面平行时，则该直线与两个平面成等角；反之，如果一条直线与两个平面成等角，这两个平面可能是相交平面．如下图，α⊥β，直线AB 与α、β都成45°角，但α∩β＝l .4．在正方体ABCD －A 1B 1C 1D 1中，棱长为a ，M 、N 分别为A 1B 和AC 上的点，A 1M ＝AN ＝2a3，则MN 与平面BB 1C 1C 的位置关系是( )A ．相交B ．平行C ．垂直D ．不能确定 答案 B解析 连接CD 1，在CD 1上取点P ，使D 1P ＝2a3，∴MP ∥BC ，PN ∥AD 1∴MP ∥面BB 1C 1C ，PN ∥面AA 1D 1D ， ∴面MNP ∥面BB 1C 1C ，∴MN ∥面BB 1C 1C .5．设α、β、γ为两两不重合的平面，l 、m 、n 为两两不重合的直线．给出下列四个命题：①若α⊥γ，β⊥γ，则α∥β；②若m ⊂α，n ⊂α，m ∥β，n ∥β，则α∥β；③若α∥β，l⊂α，则l∥β；④若α∩β＝l，β∩γ＝m，γ∩α＝n，l∥γ，则m∥n.其中真命题的个数是( )A．1 B．2C．3 D．4答案 B解析①∵垂直于同一个平面的两个平面也可以相交，如墙角，∴该命题不对；②m、n 相交时才有α∥β，此命题不对；③由面面平行的性质定理可知该命题正确；④∵l∥γ，β∩γ＝m，l⊂β，∴l∥m，又α∩β＝l，且m⊂β，∴m∥α，又m⊂γ且γ∩α＝n，∴m∥n，故④对，选B.6．如图所示，四个正方体图形中，A、B为正方体的两个顶点，M、N、P分别为其所在棱的中点，能得出AB∥面MNP的图形的序号是________(写出所有符合要求的图形序号)．答案①③7．考察下列三个命题，在“________”处都缺少同一个条件，补上这个条件使其构成真命题(其中l、m为直线，α、β为平面)，则此条件为________．①⎭⎪⎬⎪⎫m⊂αl∥m⇒l∥α；②⎭⎪⎬⎪⎫l∥mm∥α⇒l∥α；③⎭⎪⎬⎪⎫l⊥βα⊥β⇒l∥α.答案l⊄α解析①体现的是线面平行的判定定理，缺的条件是“l为平面α外的直线”，即“l ⊄α”，它也同样适合②③，故填l⊄α.8．在四面体ABCD中，M、N分别是面△ACD、△BCD的重心，则四面体的四个面中与MN 平行的是________．答案平面ABC和平面ABD解析连接AM并延长交CD于E，连接BN并延长交CD于F.由重心的性质可知，E、F 重合为一点，且该点为CD的中点E.由EMMA＝ENNB＝12得MN∥AB.因此，MN∥平面ABC且MN∥平面ABD.9．设x，y，z为空间不同的直线或不同的平面，且直线不在平面内，下列说法中能保证“若x⊥z，y⊥z，则x∥y”为真命题的序号有________．(把所有的真命题全填上)①x为直线，y，z为平面；②x，y，z都为平面；③x，y为直线，z为平面；④x，y，z都为直线，⑤x，y为平面，z为直线．答案③⑤解析①直线x可能在平面y内；②平面x与y可能相交；④直线x与y可能相交，也可能异面，故③⑤正确．10．(2011·天津文)如图，在四棱锥P－ABCD中，底面ABCD为平行四边形，∠ADC＝45°，AD＝AC＝1，O为AC的中点，PO⊥平面ABCD，PO＝2，M为PD的中点．证明：PB∥平面ACM.解析连接BD，MO，在平行四边形ABCD中，因为O为AC的中点，所以O为BD的中点．又M为PD的中点，所以PB∥MO.因为PB⊄平面ACM，MO⊂平面ACM，所以PB∥平面ACM.11. 如图所示，已知ABCD－A1B1C1D1是棱长为3的正方体，点E在AA1上，点F在CC1上，G在BB1上，且AE＝FC1＝B1G＝1，H是B1C1的中点．(1)求证：E 、B 、F 、D 1四点共面； (2)求证：平面A 1GH ∥平面BED 1F . 解析 (1)连接FG .∵AE ＝B 1G ＝1，∴BG ＝A 1E ＝2， ∴BG 綊A 1E ，∴A 1G ∥BE . 又∵C 1F 綊B 1G ，∴四边形C 1FGB 1是平行四边形，∴FG 綊C 1B 1綊D 1A 1，∴四边形A 1GFD 1是平行四边形． ∴A 1G 綊D 1F ，∴D 1F 綊EB ， 故E 、B 、F 、D 1四点共面．(2)∵H 是B 1C 1的中点，∴B 1H ＝32.又B 1G ＝1，∴B 1G B 1H ＝23. 又FC BC ＝23，且∠FCB ＝∠GB 1H ＝90°， ∴△B 1HG ∽△CBF ，∴∠B 1GH ＝∠CFB ＝∠FBG ，∴HG ∥FB . 又由(1)知，A 1G ∥BE ， 且HG ∩A 1G ＝G ，FB ∩BE ＝B ， ∴平面A 1GH ∥平面BED 1F .12. 如图，三棱柱ABC －A 1B 1C 1，底面为正三角形，侧棱A 1A ⊥底面ABC ，点E 、F 分别是棱CC 1、BB 1上的点，点M 是线段AC 上的动点，EC ＝2FB .当点M 在何位置时，BM ∥平面AEF?解析 方法一 如图，取AE 的中点O ，连接OF ，过点O 作OM ⊥AC 于点M .∵侧棱A 1A ⊥底面ABC ， ∴侧面A 1ACC 1⊥底面ABC ， ∴OM ⊥底面ABC . 又∵EC ＝2FB ， ∴OM ∥FB 綊12EC ，∴四边形OMBF 为矩形， ∴BM ∥OF ，又∵OF ⊂面AEF ，BM ⊄面AEF .故BM ∥平面AEF ，此时点M 为AC 的中点．方法二如图，取EC的中点P，AC的中点Q，连接PQ、PB、BQ，∴PQ∥AE.∵EC＝2FB，∴PE綊BF，PB∥EF，∴PQ∥平面AEF，PB∥平面AEF.又PQ∩PB＝P，∴平面PBQ∥平面AEF，又∵BQ⊂面PQB，∴BQ∥平面AEF.故点Q即为所求的点M，此时点M为AC的中点．13．(2011·山东文) 如图，在四棱台ABCD－A1B1C1D1中，D1D⊥平面ABCD，底面ABCD 是平行四边形，AB＝2AD，AD＝A1B1，∠BAD＝60°.(1)证明：AA1⊥BD；(2)证明：CC1∥平面A1BD.解析(1)证法一因为D1D⊥平面ABCD，且BD⊂平面ABCD，所以D1D⊥BD.又因为AB＝2AD，∠BAD＝60°，在△ABD中，由余弦定理得BD2＝AD2＋AB2－2AD·AB cos60°＝3AD2，所以AD2＋BD2＝AB2，因此AD⊥BD.又AD∩D1D＝D，所以BD⊥平面ADD1A1.又AA1⊂平面ADD1A1，故AA1⊥BD.证法二因为D1D⊥平面ABCD，且BD⊂平面ABCD，所以BD⊥D1D.取AB的中心G，连接DG，在△ABD中，由AB＝2AD得AG＝AD，又∠BAD＝60°，所以△ADG为等边三角形，因此GD＝GB，故∠DBG＝∠GDB，又∠AGD＝60°，所以∠GDB＝30°，故∠ADB＝∠ADG＋∠GDB＝60°＋30°＝90°，所以BD⊥AD.又AD∩D1D＝D，所以BD⊥平面ADD1A1.又AA1⊂平面ADD1A1，故AA1⊥BD.(2)连接AC，A1C1，设AC∩BD＝E，连接EA1，因为四边形ABCD 为平行四边形， 所以EC ＝12AC .由棱台定义及AB ＝2AD ＝2A 1B 1，知A 1C 1∥EC 且A 1C 1＝EC ， 所以四边形A 1ECC 1为平行四边形，因此CC 1∥EA 1. 又因为EA 1⊂平面A 1BD ，CC 1⊄平面A 1BD ， 所以CC 1∥平面A 1BD .1．如下图所示，在四棱锥P －ABCD 中，ABCD 是平行四边形，M 、N 分别是AB 、PC 的中点，求证：MN ∥平面PAD .证明 方法一 取CD 中点E ， 连接NE 、ME .∵M 、N 分别是AB 、PC 的中点，∴NE ∥PD ，ME ∥AD .∴NE ∥平面PAD ，ME ∥平面PAD .又NE ∩ME ＝E ，∴平面MNE ∥平面PAD .又MN ⊂平面MNE ，∴MN ∥平面PAD .方法二 取PD 中点F ，连接AF 、NF .∵M 、N 分别为AB 、PC 的中点， ∴NF 綊12CD ，AM 綊12CD ， ∴AM 綊NF .∴四边形AMNF 为平行四边形，∴MN ∥AF .又AF ⊂平面PAD ，MN ⊄平面PAD ，∴MN ∥平面PAD .2．在正方体ABCD－A1B1C1D1中，M，N，P分别是C1C，B1C1，C1D1的中点，求证：平面MNP ∥平面A1BD.证明方法一如图(1)所示，连接B1D1.∵P，N分别是D1C1，B1C1的中点，∴PN∥B1D1.又B1D1∥BD，∴PN∥BD.又PN⊄平面A1BD，∴PN∥平面A1BD.同理：MN∥平面A1BD.又PN∩MN＝N，∴平面PMN∥平面A1BD.方法二如图(2)所示，连接AC1，AC，∵ABCD－A1B1C1D1为正方体，∴AC⊥BD.又CC1⊥平面ABCD，∴AC为AC1在平面ABCD上的射影，∴AC1⊥BD.同理可证AC1⊥A1B，∴AC1⊥平面A1BD.同理可证AC1⊥平面PMN.∴平面PMN∥平面A1BD.3. 如图，在正三棱柱ABC－A1B1C1中，点D在边BC上，AD⊥C1D.(1)求证：AD⊥平面BCC1B1；(2)设E是B1C1上的一点，当B1EEC1的值为多少时，A1E∥平面ADC1？请给出证明．解析(1)在正三棱柱中，CC1⊥平面ABC，AD⊂平面ABC，∴AD⊥CC1.又AD⊥C1D，CC1交C1D于C1，且CC1和C1D都在平面BCC1B1内，∴AD⊥平面BCC1B1.(2)由(1)得AD⊥BC.在正三角形ABC中，D是BC的中点．当B1EEC1＝1，即E为B1C1的中点时，A1E∥平面ADC1.在正三棱柱ABC－A1B1C1中，四边形BCC1B1是矩形，且D、E分别是BC、B1C1的中点，∴B1B∥DE，B1B＝DE.又B1B∥AA1，且B1B＝AA1，∴DE∥AA1，且DE＝AA1.∴四边形ADEA1为平行四边形，∴A1E∥AD.而A1E⊄平面ADC1，故A1E∥平面ADC1.1．如图在正四棱柱ABCD－A1B1C1D1中，E、F、G、H分别是棱CC1、C1D1、D1D、DC的中点，N是BC的中点，点M在四边形EFGH及其内部运动，则M满足条件________时，有MN∥平面B1BDD1.答案M∈线段FH解析∵HN∥BD，HF∥DD1，∴平面NHF∥平面B1BDD1.故线段FH上任一点M与N相连，都有MN∥平面B1BDD1，故填M∈线段FH.2. 如图所示，四棱锥P－ABCD的底面是边长为a的正方形，侧棱PA⊥底面ABCD，在侧面PBC内，有BE⊥PC于E，且BE＝63a，试在AB上找一点F，使EF∥平面PAD.解析在平面PCD内，过E作EG∥CD交PD于G，连接AG，在AB上取点F，使AF＝EG，则F即为所求作的点．∵EG∥CD∥AF，EG＝AF，∴四边形FEGA为平行四边形，∴FE∥AG.又AG⊂平面PAD，FE⊄平面PAD，∴EF ∥平面PAD .又在△BCE 中，CE ＝BC 2－BE 2＝a 2－23a 2 ＝33a . 在Rt △PBC 中，BC 2＝CE ·CP ， ∴CP ＝a 233a ＝3a .又EG CD ＝PE PC， ∴EG ＝AF ＝23a . ∴点F 为AB 的一个三等分点，且靠近B 点．e30655 77BF 瞿u35844 8C04 谄/N33780 83F4 菴j39500 9A4C 驌27083 69CB 構&,23426 5B82 宂Z22533 5805 堅。

人教A 版必修2第二章2.2.3《直线与平面平行的性质》精选题高频考点（含答案)-1学校:___________姓名：___________班级：___________考号：___________一、单选题1．如图，在长方体1111ABCD A B C D -中，E 、F 分别是棱1AA 和1BB 的中点，过EF 的平面EFGH 分别交BC 和AD 于点G 、H ，则GH 与AB 的位置关系是（ ）A ．平行B ．相交C ．异面D ．平行或异面 2．如图所示，在四棱锥P ABCD -中，M N ，分别为AC PC ，上的点，且MN ∥平面PAD ，则（ ）A ．MN PD PB ．MN PA ∥C ．MN AD P D ．以上均有可能 3．如图，P 为平行四边形ABCD 所在平面外一点，E 为AD 上一点，且13AE ED =，F 为PC 上一点，当//PA 平面EBF 时，PF FC=（ ）A ．23B ．14C ．13D ．12 4．如图所示，在长方体1111ABCD A B C D -中，121AB BC AA ，===，则1BC 与平面11BB D D 所成角的正弦值为（ ）A．3 BC．5 D．5 5．在正方体1111ABCD A B C D -中，E 为棱CD 上一点，且2CE DE =，F 为棱1AA 的中点，且平面BEF 与1DD 交于点G ，与1AC 交于点H ，则（ ）A ．115DG DD =B ．113AH HC = C ．114DG DD = D ．138AH HC = 6．如图，1111ABCD A B C D -是正方体，E 为棱1BB 上的动点（不含端点），平面11AC E 与底面ABCD 的交线为l ，则l 与AC 的位置关系是（ ）A ．异面B ．平行C ．相交D ．与E 点位置有关 7．已知m ，n 是不同的直线，α，β是不重合的平面，下列命题中正确的有（ ） ①若m α⊥，m β⊥，则//αβ②若//m α，m β⊂，n αβ=I ，则//m n③若//m α，//m β，则//αβ④若αβ⊥，m α⊂，n β⊂，则m n ⊥A ．①②B ．①③C ．②④D ．③④ 8．已知//,a b αα⊂，则直线a 与直线b 的位置关系是（ ）A ．平行B ．相交或异面C ．异面D ．平行或异面 9．已知棱长为3的正方体1111ABCD A B C D -,点E 是棱AB 的中点，12CF FC =u u u r u u u u r ，动点P 在正方形11AA DD （包括边界）内运动，且1PB P 面DEF ，则PC 的长度范围为（ ）A ．B ．5⎡⎢⎣C ．5⎡⎢⎣D ．5⎡⎢⎣10．如图，各棱长均为a 的正三棱柱111ABC A B C -，M 、N 分别为线段1A B 、1B C 上的动点，且MN ∥平面11ACC A ，M ，N 中点S 111ABC A B C -的体积为（ ）A B C ．3 D ．11．点E ，F 分别是棱长为1的正方体1111ABCD A B C D -中棱BC ，1CC 的中点，动点P 在正方形11BCC B （包括边界）内运动，且1PA ∥面AEF ，则1PA 的长度范围为（ ）A ．1,2⎡⎢⎣⎦B ．42⎡⎢⎣⎦C ．342⎡⎤⎢⎥⎣⎦D ．31,2⎡⎤⎢⎥⎣⎦12．如图，在正四棱锥S －ABCD 中，E ，M ，N 分别是BC ，CD ，SC 的中点，动点P在线段MN 上运动时，下列四个结论：①EP ⊥AC ；②EP ∥BD ；③EP ∥平面SBD ；④EP ⊥平面SAC ，其中恒成立的为( )A ．①③B ．③④C ．①②D ．②③④13．一条直线若同时平行于两个相交平面，那么这条直线与这两个平面交线的位置关系是（ ）A ．异面B ．相交C ．不能确定D ．平行 14．如图所示，a P α，A 是α的另一侧的点，B C D a ∈，，，线段AB AC AD ，，分别交α于点EFG ，，，若445BD CF AF ===，，，则EG =（ ）A ．169B ．209C ．94D ．5415．如图，已知四棱锥P ABCD -的底面是平行四边形，AC 交BD 于点O ，E 为AD 中点，F 在PA 上，AP AF λ=，//PC 平面BEF ，则λ的值为（ ）A ．1B ．32C ．2D ．3 16．给出下列关于互不相同的直线,,l m n 和平面,,αβγ的三个命题：①若l 与m 为异面直线，,l m αβ⊂⊂，则//αβ；②若//,,l m αβαβ⊂⊂，则//l m ；③若,,,//l m n l αββγγαγ===I I I ，则//m n ．其中正确的个数为（ ）A ．0B ．1C ．2D ．317．如图，P 为平行四边形ABCD 所在平面外一点，E 为AD 的中点，F 为PC 上一点，当P A ∥平面EBF 时，PF FC＝（ ）A ．23B ．14C ．13D ．12 18．如果直线m//直线n ，且m//平面α，那么n 与α的位置关系是（） A ．相交 B ．n//α C ．n ⊂α D ．n//α或n ⊂α 19．若直线a 平行于平面α，则下列结论错误的是（ ）A ．直线a 上的点到平面α的距离相等B ．直线a 平行于平面α内的所有直线C ．平面α内有无数条直线与直线a 平行D ．平面α内存在无数条直线与直线a 所成的角为90o20．已知l ，m 为两条不同直线，α，β为两个不同平面.则下列命题正确的是（ ） A ．若l αP ，m α⊂，则l m PB ．若l αP ，m αP ，则l m PC ．若l α⊂，m β⊂，αβ∥，则l m PD ．若l αP ，l β∥，m αβ=I ，则l m P二、填空题21．如图,正方体1111ABCD A B C D -中, AB =点E 为11A D 的中点,点F 在11C D 上,若//EF 平面1ACB ,则EF =________．22．在正方体1111ABCD A B C D -中，E 为棱CD 上一点，且2CE DE =，F 为棱1AA 的中点，且平面BEF 与1DD 交于点G ，与1AC 交于点H ，则1DG DD =______，1AH HC =______. 23．如图所示，a ∥α，A 是α的另一侧的点，B 、C 、D ∈a ，线段AB 、AC 、AD 交α于E 、F 、G ，若BD ＝4，CF ＝4，AF ＝5，则EG ＝________．24．如图，E 是棱长为1正方体1111ABCD A B C D -的棱11C D 上的一点，且1//BD 平面1B CE ，则线段CE 的长度为___________．25．如图所示，四面体ABCD 被一平面所截，截面EFGH 是一个矩形．则直线CD 与平面EFGH 的关系是______．26．如图在四面体ABCD 中，若截面PQMN 是正方形，则在下列命题中正确的有______.(填上所有正确命题的序号)AC BD ⊥①，AC BD =②，//AC ③截面PQMN ，④异面直线PM 与BD 所成的角为45o ．27．在三棱锥S ABC -中，ABC ∆是边长为4的正三角形，10SA SB SC ===，平面DEFH 分别与AB ，BC ，SC ，SA 交于D ，E ，F ，H 且D ，E 分别是AB ，BC 的中点，如果直线SB P 平面DEFH ，那么四边形DEFH 的面积为______．28．已知l 、m 是两条直线，α是平面，若要得到“l ∥α”，则需要在条件“m ⊂α，l ∥m ”中另外添加的一个条件是______.29．如图，DC ⊥平面ABC ，EB ∥DC ，EB ＝2DC ，P ，Q 分别为AE ，AB 的中点．则直线DP 与平面ABC 的位置关系是________．30．正方体1111ABCD A B C D -中,2AB =,点E 为AD 的中点,点F 在1CC 上,若//EF 平面1AB C ,则EF =_____.31．如图所示，在三棱柱111ABC A B C -中，过11A B C ，，的平面与平面ABC 的交线为l ，则l 与直线11A C 的位置关系为________.32．如图所示，长方体1111ABCD A B C D -的底面ABCD 是正方形，其侧面展开图是边长为8的正方形，E F ，分别是侧棱11AA CC ，上的动点，且8AE CF +=，P 在棱1AA 上，且2AP =，若EF P 平面PBD ，则CF =________.33．如图所示，在三棱柱111ABC A B C 中，E F G H ，，，分别是1111AB AC A B A C ，，，的中点，则与平面BCHG 平行的平面为________.34．如图（1）所示，已知正方形ABCD 中，E F ，分别是AB ，CD 的中点，将ADE V 沿DE 折起，如图（2）所示，则BF 与平面ADE 的位置关系是________.35．已知A 、B 、C 、D 四点不共面，且AB ∥平面α，CD ∥α，AC ∩α＝E ，AD ∩α＝F ，BD ∩α＝H ，BC ∩α＝G ，则四边形EFHG 是_______四边形.36．如图，棱长为2的正方体1111ABCD A B C D -中，M 是棱AA 1的中点，过C ，M ，D 1作正方体的截面，则截面的面积是________．37．如图所示，在长方体1111ABCD A B C D -中，111BB B D =，点E 是棱1CC 上的一个动点，若平面1BED 交棱1AA 于点F ，给出下列命题：.① 四棱锥11B BED F -的体积恒为定值；②存在点E ，使得1B D ⊥平面1BD E ；③存在唯一的点E ，使得截面四边形1BED F 的周长取得最小值；④存在无数个点E ，在棱AD 上均有相应的点G ，使得CG P 平面1EBD ，也存在无数个点E ，对棱AD 上任意的点G ， 直线CG 与平面1EBD 均相交.其中真命题的是____________．（填出所有正确答案的序号）38．已正知方体ABCD-A 1B 1C 1D 1的棱长为2，点P 是平面AA 1D 1D 的中心，点Q 是B 1D 1上一点，且PQ ∥平面AB 1D ，则线段PQ 长为______．39．设,a b 是平面M 外两条直线，且//a M ，那么//a b 是//b M 的________条件.40． 已知正方体ABCD －A 1B 1C 1D 1的棱长为1，点P 是平面AA 1D 1D 的中心，点Q 是平面A 1B 1C 1D 1的对角线B 1D 1上一点，且PQ ∥平面AA 1B 1B ，则线段PQ 的长为________．三、解答题41．如图，四棱锥P ABCD -中，底面ABCD 为矩形，侧面PAD 为正三角形，2AD =，3AB =，平面PAD ⊥平面ABCD ，E 为棱PB 上一点（不与P 、B 重合），平面ADE 交棱PC 于点F .（1）求证：AD EF P ；（2）若二面角––B AC E ，求点B 到平面AEC 的距离. 42．如图，在四棱锥P ABCD -中，底面ABCD 是梯形，且//BC AD ，2AD BC =，点Q 是线段AD 的中点，过BQ 的平面BQMN 交平面PCD 于MN ，且PQ AB ⊥，AP PD =，且120APD ∠=︒，24BD AB ==，30ADB ∠=︒.（1）求证：//BQ MN ；（2）求直线PA 与平面PCD 所成角的余弦值.43．如图所示的一块木料中，棱BC 平行于面A C ''.（1）要经过面A C ''内的一点P 和棱BC 将木料锯开，在木料表面应该怎样画线？ （2）所画的线与平面AC 是什么位置关系？44．如图，已知E ，F 分别是正方体1111ABCD A B C D -的棱1AA ，1CC 上的点，且1AE C F =.求证：四边形1EBFD 是平行四边形.45．如图所示，P 是平行四边形ABCD 所在平面外一点，E 是PD 的中点、若M 是CD 上异于C ，D 的点，连接PM 交CE 于点G ，连接BM 交AC 于点H ，连接GH ，求证：GH //PB .46．已知如图，斜三棱柱ABC -A 1B 1C 1中，点D 、D 1分别为AC 、A 1C 1上的点． （1）当1111A D D C 等于何值时，BC 1∥平面AB 1D 1？ （2）若平面BC 1D ∥平面AB 1D 1，求AD DC的值．47．如图所示，已知三棱柱ABC-A'B'C'中，D 是BC 的中点，D'是B'C'的中点，设平面A'D'B∩平面ABC=a ，平面ADC'∩平面A'B'C'=b ，判断直线a ，b 的位置关系，并证明．48．如图，四棱锥P ABCD -的底面ABCD 为直角梯形，//AD BC ，且112BC AD ==，BC DC ⊥，60BAD ∠=︒，平面PAD ⊥底面ABCD ，E 为AD 的中点，PAD ∆为等边三角形，M 是棱PC 上的一点，设PM k MC=（M 与C 不重合）.（1）当1k =时，求三棱锥M BCE -的体积；（2）若//PA 平面BME ，求k 的值.49．如图，E ，F ，G ，H 分别是空间四边形ABCD 各边上的点，且::AE EB AH HD m ==，::CF FB CG GD n ==.（1）证明：E ，F ，G ，H 四点共面.（2）m ，n 满足什么条件时，四边形EFGH 是平行四边形？50．如图，在四校锥P ABCD -中，底面ABCD 为正方形，平面PAD ⊥平面ABCD ，点M 在线段PB 上，//PD 平面MAC ，PA PD ==4AB =.求证：M 为PB 的中点.参考答案1．A2．B3．B4．D5．D6．B7．A8．D9．B10．D11．B12．A13．D14．B15．D16．B17．D18．D19．B20．D21．222．163823．20 92425．平行26．①③④27．10 28．lα⊄29．平行3031．平行. 32．2. 33．平面1A EF 34．平行35．平行【答案】9 237．①②③④3839．充分不必要40．241．（1）证明见解析；（2.42．（1）证明见解析（243．（1）见解析（2）直线EF与平面AC平行直线,BE CF与平面AC相交. 44．证明见解析45．证明见解析46．（1）1；（2）1.47．直线a，b的位置关系是平行，证明见试题解析．48．（1）14；（2）1.49．（1）见解析（2）当m n时，四边形EFGH是平行四边形. 50．证明见解析。

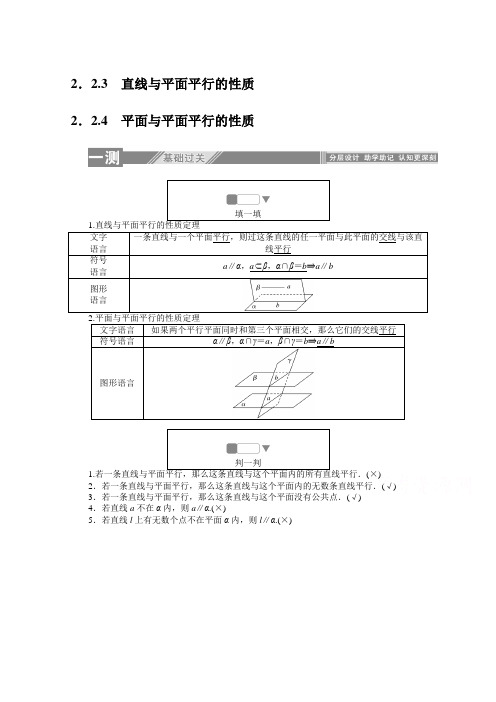
2．2.3直线与平面平行的性质2．2.4平面与平面平行的性质填一填1.直线与平面平行的性质定理文字语言一条直线与一个平面平行，则过这条直线的任一平面与此平面的交线与该直线平行符号语言a∥α，a⊂β，α∩β＝b⇒a∥b图形语言2.平面与平面平行的性质定理文字语言如果两个平行平面同时和第三个平面相交，那么它们的交线平行符号语言α∥β，α∩γ＝a，β∩γ＝b⇒a∥b图形语言判一判1.(×) 2．若一条直线与平面平行，那么这条直线与这个平面内的无数条直线平行．(√) 3．若一条直线与平面平行，那么这条直线与这个平面没有公共点．(√)4．若直线a不在α内，则a∥α.(×)5．若直线l上有无数个点不在平面α内，则l∥α.(×)6.若两个平面平行，那么分别在这两个平面内的直线互相平行．(×)7．若两个平面平行，那么其中一个平面内的任意一条直线与另一个平面平行．(√)8．已知两个平面平行，若有第三个平面与其中的一个平面平行，那么它与另一平面也平行．(√)想一想1.两个平面平行，那么两个平面内的所有直线都相互平行吗？提示：不一定．因为两个平面平行，所以这两条直线无公共点，它们平行或异面．2．两个平面平行，其中一个平面内直线必平行于另一个平面吗？提示：平行．因为两个平面平行，则两个平面无公共点，则其中一个平面内的直线必和另一个平面无公共点，所以它们平行．3．利用线面平行性质定理解题的步骤是什么？提示：4．应用平面与平面平行性质定理的基本步骤是什么？提示：思考感悟：练一练1.如图所示，在空间四边形ABCD中，E，F，G，H分别是AB，BC，CD，DA上的点，EH∥FG，则EH与BD的位置关系是()A．平行B．相交C．异面D．不确定答案：A2．如图，在三棱锥S－ABC中，E，F分别是SB，SC上的点，且EF∥平面ABC，则() A．EF与BC相交B．EF∥BCC．EF与BC异面D．以上均有可能答案：B3．如图所示的三棱柱ABC－A1B1C1，过A1B1的平面与平面ABC交于直线DE，则DE与AB的位置关系是()A．异面B．平行C．相交D．以上均有可能答案：B4．已知两个不同的平面α，β和两条不重合的直线m，n，有下列四个命题：①若m∥n，n⊂α，则m∥α②若m∥α，n∥α，且m⊂β，n⊂β，则α∥β③m∥α，n ⊂α，则m∥n④若α∥β，m⊂α，则m∥β，其中正确的个数是()A．1 B．2C．3 D．4答案：A知识点一直线与平面平行的性质定理的理解①m，n⊂β②n⊂α③m∥α④m∥n.现把其中一些关系看作条件，另一些看作结论，组成一个真命题是________．解析：结合线面平行的性质定理，可知①②③⇒④，结合线面平行的判定定理，可知①②④⇒③.答案：①②③⇒④或①②④⇒③2．直线a∥平面α，α内有n条直线交于一点，则这n条直线中与直线a平行的直线有() A．0条B．1条C．0或1条D．无数条解析：与a平行的可能有0或1条．知识点二平面与平面平行性质定理的理解3.()①若a∥α，b∥α，则a∥b②若a∥α，a∥β，则α∥β③若α∥β，a⊂α，则a∥βA．0个B．1个C．2个D．3个解析：①当a，b共面时，满足a∥b或a，b相交；当a，b不共面时，a与b为异面直线．故不正确．②若a∥α，a∥β，则α∥β或α，β相交．故不正确．③根据两平面平行的性质．正确．故选B.答案：B4．已知直线a∥平面α，a∥平面β，α∩β＝b，则a与b()A．相交B．平行C．异面D．共面或异面解析：∵直线a∥α，a∥β，∴在平面α，β中必分别有一直线平行于a，不妨设为m，n，∴a∥m，a∥n，∴m∥n.又α，β相交，m在平面α内，n在平面β内，∴m∥β，∴m∥b，∴a∥b.故选B.知识点三直线与平面平行的性质定理的应用如图，四棱锥P－ABCD中，M，N分别为AC，PC上的点，且MN∥平面P AD，则() A．MN∥PDB．MN∥P AC．MN∥ADD．以上均有可能解析：四棱锥P－ABCD中，M，N分别为AC，PC上的点，且MN∥平面P AD，因为MN ⊂平面P AC，平面P AC∩平面P AD＝P A，所以由直线与平面平行的性质定理可得，MN∥P A.答案：B6．如图，在长方体ABCD－A1B1C1D1中，点P∈BB1(P不与B，B1重合)．P A∩A1B＝M，PC∩BC1＝N.求证：MN∥平面ABCD.证明：如图，连接AC，A1C1，在长方体ABCD－A1B1C1D1中，AA1∥CC1，且AA1＝CC1，所以四边形ACC 1A 1是平行四边形． 所以AC ∥A 1C 1.因为AC ⊄平面A 1BC 1，A 1C 1⊂平面A 1BC 1， 所以AC ∥平面A 1BC 1.因为AC ⊂平面P AC ，平面A 1BC 1∩平面P AC ＝MN ， 所以AC ∥MN .因为MN ⊄平面ABCD ，AC ⊂平面ABCD ， 所以MN ∥平面ABCD .综合知识 平面与平面平行的性质定理的应用如图，正方体ABCD －A 1B 1C 1D 1中过BD 1的平面，分别与AA 1，CC 1交于M ，N ，则四边形BND 1M 的形状为________．解析：由题意知，平面A 1ABB 1∥平面C 1CDD 1， 所以MB ∥D 1N ，同理，D 1M ∥BN . 所以四边形BND 1M 是平行四边形． 答案：平行四边形 8.如图所示，已知正方体ABCD －A 1B 1C 1D 1中，面对角线AB 1，BC 1上分别有两点E ，F ，且B 1E ＝C 1F .求证：EF ∥平面ABCD .解析：证明：过E 作EG ∥AB 交BB 1于G ， 连接GF ，所以B 1E B 1A ＝B 1G B 1B，B 1E ＝C 1F ，B 1A ＝C 1B ，所以C 1F C 1B ＝B 1G B 1B，所以FG ∥B 1C 1∥BC .又因为EG ∩FG ＝G ，AB ∩BC ＝B ，所以平面EFG ∥平面ABCD .又EF ⊂平面EFG ， 综合知识 线面平行、面面平行的性质定理9.四棱锥P －ABCD 的底面ABCD 是梯形，AB ∥CD ，且AB ＝23CD .试问在PC 上能否找到一点E ，使得BE ∥平面P AD ？若能，请确定E 点的位置，并给出证明；若不能，请说明理由．解析：在PC 上取点E ，使CE PE ＝12，则BE ∥平面P AD .证明如下：延长DA 和CB 交于点F ，连接PF .在梯形ABCD 中，AB ∥CD ，AB ＝23CD .所以AB CD ＝BF FC ＝23，所以BC BF ＝12.又CE PE ＝12，所以在△PFC 中，CE PE ＝BC BF ， 所以BE ∥PF ，而BE ⊄平面P AD ，PF ⊂平面P AD . 所以BE ∥平面P AD .基础达标一、选择题1．若一条直线和一个平面平行，夹在直线和平面间的两条线段相等，那么这两条线段所在直线的位置关系是( )A ．平行B ．相交C ．异面D ．平行、相交或异面解析：作出图形，如图所示：在正方体ABCD －A 1B 1C 1D 1中，A 1B 1∥ABCD .A 1B 与AB 1，相交．AA 1∥BB 1，A 1B 与B 1C 异面．故选D. 答案：D2．如果一条直线与两个平行平面中的一个平行，那这条直线与另一个平面的位置关系是( )A ．平行B ．相交C ．在平面内D ．平行或在平面内解析：由题这条直线与另一个平面平行或者直线在平面上．故选D. 答案：D3．已知两条相交直线a，b，a∥平面α，则b与α的位置关系是()A．b⊂平面αB．b∥α或b⊂αC．b∥平面αD．b与平面α相交或b∥平面α解析：b与a相交，可确定一个平面，记为β，若β与α平行，则b∥α；若β与α不平行，则b与α相交．答案：D4．已知平面α∥平面β，直线a⊂α，直线b⊂β，则①a∥b②a，b为异面直线③a，b 一定不相交④a∥b或a，b异面，其中正确的是()A．①②B．②③C．③④D．①②③④解析：∵平面α∥平面β.∴α与β没有公共点．∵直线a⊂α，直线b⊂β.∴a与b没有公共点．即a与b一定不相交．∴a∥b或a与b为异面直线．选C.答案：C5.如图，在多面体ABC－DEFG中，平面ABC∥平面DEFG，EF∥DG，且AB＝DE，DG ＝2EF，则()A．BF∥平面ACGDB．CF∥平面ABEDC．BC∥FGD．平面ABED∥平面CGF解析：取DG的中点为M，连接AM，FM，如图所示．则由已知条件易证四边形DEFM 是平行四边形，∴DE綊FM.∵平面ABC∥平面DEFG，平面ABC∩平面ADEB＝AB，平面DEFG∩平面ADEB＝DE，∴AB∥DE，∴AB∥FM.又AB＝DE，∴AB＝FM，∴四边形ABFM是平行四边形，即BF∥AM.又BF⊄平面ACGD，∴BF∥平面ACGD.故选A.答案：A6.如图，在三棱柱ABC －A 1B 1C 1中，点D 为AC 的中点，点D 1是A 1C 1上的一点，若BC 1∥平面AB 1D 1，则A 1D 1D 1C 1等于( )A.12B ．1C ．2D ．3解析：可证AD 1∥DC 1，所以D 1为A 1C 1中点． 答案：B 7.如图，在三棱台A 1B 1C 1－ABC 中，点D 在A 1B 1上，且AA 1∥BD ，点M 是△A 1B 1C 1内的一个动点，且有平面BDM ∥平面A 1C 1CA .则动点M 的轨迹是( )A ．平面B ．直线C ．线段，但只含1个端点D ．圆解析：因为平面BDM ∥平面A 1C 1CA ，平面BDM ∩平面A 1B 1C 1＝DM ，平面A 1C 1CA ∩平面A 1B 1C 1＝A 1C 1，所以DM ∥A 1C 1，过D 作DE ∥A 1C 1交B 1C 1于E ，则点M 的轨迹是线段DE (不包括点D )． 答案：C 二、填空题8．一个面截空间四边形的四边得到四个交点，如果该空间四边形的两条对角线与这个截面平行，那么此四个交点围成的四边形是________．解析：由线面平行的性质定理可得四个交点围成的四边形为平行四边形． 答案：平行四边形 9.如图，正方体ABCD －A 1B 1C 1D 1中，AB ＝2，点E 为AD 的中点，点F 在CD 上．若EF ∥平面AB 1C ，则线段EF 的长度等于________．解析：因为直线EF ∥平面AB 1C ，EF ⊂平面ABCD ，且平面AB 1C ∩平面ABCD ＝AC ，所以EF ∥AC ，因为E 是DA 的中点，所以F 是DC 的中点，由中位线定理可得EF ＝12AC ，在正方体ABCD －A 1B 1C 1D 1中，AB ＝2，AC ＝22，所以EF ＝ 2.答案： 2 10.如图，过正方体ABCD －A 1B 1C 1D 1的顶点B 1，D 1与棱AB 的中点P 的平面与底面ABCD 所在平面的交线记为l ，则l 与B 1D 1的位置关系为________．解析：如图所示，在正方体ABCD－A1B1C1D1中，平面ABCD∥平面A1B1C1D1，且平面B1D1P∩平面A1B1C1D1＝B1D1，平面B1D1P∩平面ABCD＝l，所以l∥B1D1.答案：l∥B1D111．如图，α∩β＝CD，α∩γ＝EF，β∩γ＝AB，AB∥α，则CD与EF的位置关系为________．解析：由线面平行的性质得，AB∥CD，AB∥EF，由公理4得CD∥EF.答案：平行12．如图，在正方体ABCD－A1B1C1D1中，E，F，G，H分别为CC1，C1D1，D1D，CD 的中点，N是BC的中点，点M在四边形EFGH及其内部运动，则M满足________时，MN∥平面BDD1B1.解析：如图，取B1C1的中点P，连接NP，NH，HF，PF，则可证明平面NPFH∥平面BDD1B1，若MN⊂平面NPFH，则MN∥平面BDD1B1.答案：M∈FH.(答案不唯一，如FH∩GE＝M等)三、解答题13.如图，在四棱柱ABCD－A1B1C1D1中，底面ABCD为梯形，AD∥BC，平面A1DCE与B1B 交于点E.求证：EC∥A1D.证明：因为BE ∥AA 1，AA 1⊂平面AA 1D ，BE ⊄平面AA 1D ， 所以BE ∥平面AA 1D .因为BC ∥AD ，AD ⊂平面AA 1D ，BC ⊄平面AA 1D ， 所以BC ∥平面AA 1D .又BE ∩BC ＝B ，BE ⊂平面BCE ，BC ⊂平面BCE ， 所以平面BCE ∥平面AA 1D .又平面A 1DCE ∩平面BCE ＝EC ，平面A 1DCE ∩平面AA 1D ＝A 1D ， 所以EC ∥A 1D . 14.如图，P 为平行四边形ABCD 所在平面外一点，M ，N 分别是AB ，PC 的中点，平面P AD ∩平面PBC ＝l .(1)求证：BC ∥l .(2)MN 与平面P AD 是否平行？试证明你的结论． 解析：证明：(1)在▱ABCD 中，BC ∥AD ， BC ⊄平面P AD ，AD ⊂平面P AD ， 所以BC ∥平面P AD .又平面P AD ∩平面PBC ＝l ，且BC ⊂平面PBC ，所以BC ∥l . (2)MN ∥平面P AD .证明如下：取PD 中点E ，连接AE ，NE .因为N 是PC 的中点，所以NE 綊12CD ，又M 为AB 的中点，所以AM 綊12DC ，所以AM 綊NE ，所以四边形AMNE 为平行四边形，所以AE ∥MN . 又因为AE ⊂平面P AD ，MN ⊄平面P AD ， 所以MN ∥平面P AD .能力提升15.如图所示，四边形EFGH 为空间四边形ABCD 的一个截面，若截面为平行四边形． (1)求证：AB ∥平面EFGH ，CD ∥平面EFGH ；(2)若AB ＝4，CD ＝6，求四边形EFGH 周长的取值范围． 解析：(1)证明：∵四边形EFGH 为平行四边形，∴EF ∥HG . ∵HG ⊂平面ABD ，EF ⊄平面ABD ，∴EF ∥平面ABD . ∵EF ⊂平面ABC ，平面ABD ∩平面ABC ＝AB ， ∴EF ∥AB ，AB ⊄平面EFGH ，EF ⊂平面EFGH . ∴AB ∥平面EFGH .同理可证，CD ∥平面EFGH .(2)设EF ＝x (0<x <4)，∵四边形EFGH 为平行四边形，∴CF CB ＝x 4，则FG 6＝BF BC ＝BC －CF BC ＝1－x 4. ∴FG ＝6－32x . ∴四边形EFGH 的周长l ＝2⎝⎛⎭⎫x ＋6－32x ＝12－x . 又∵0<x <4，∴8<l <12，∴四边形EFGH 周长的取值范围是(8,12)．16．如图，在棱长为a 的正方体ABCD －A 1B 1C 1D 1中，E ，F ，P ，Q 分别是BC ，C 1D 1，AD 1，BD 的中点．(1)求证：PQ ∥平面DCC 1D 1；(2)求PQ 的长；(3)求证：EF ∥平面BB 1D 1D .解析：(1)法一 如图，连接AC ，CD 1. 因为P ，Q 分别是AD 1，AC 的中点，所以PQ ∥CD 1.又PQ ⊄平面DCC 1D 1，CD 1⊂平面DCC 1D 1，所以PQ ∥平面DCC 1D 1.法二 取AD 的中点G ，连接PG ，GQ ，则有PG ∥DD 1，GQ ∥DC ，且PG ∩GQ ＝G ， 所以平面PGQ ∥平面DCC 1D 1.又PQ ⊂平面PGQ ，所以PQ ∥平面DCC 1D 1.(2)由(1)易知PQ ＝12D 1C ＝22a . (3)法一 取B 1D 1的中点O 1，连接FO 1，BO 1，则有FO 1綊12B 1C 1. 又BE 綊12B 1C 1， 所以BE 綊FO 1.所以四边形BEFO 1为平行四边形，所以EF ∥BO 1，又EF ⊄平面BB 1D 1D ，BO 1⊂平面BB 1D 1D ， 所以EF ∥平面BB 1D 1D .法二 取B 1C 1的中点E 1，连接EE 1，FE 1，则有FE1∥B1D1，EE1∥BB1，且FE1∩EE1＝E1，所以平面EE1F∥平面BB1D1D.又EF⊂平面EE1F，所以EF∥平面BB1D1D.由Ruize收集整理。

第二章点、直线、平面之间的位置关系2.2 直线、平面平行的判定及其性质2.2.3 直线与平面平行的性质A级基础巩固一、选择题1．已知直线l∥平面α，P∈α，那么过点P且平行于l的直线()A．只有一条，不在平面α内B．只有一条，在平面α内C．有两条，不一定都在平面α内D．有无数条，不一定都在平面α内解析：如图所示，因为l∥平面α，P∈α，所以直线l与点P确定一个平面β，α∩β＝m，所以P∈m，所以l∥m且m是唯一的．答案：B2．如果l∥平面α，则l平行于α内()A．全部直线B．唯一确定的直线C．任一直线D．过l的平面与α的交线解析：利用线面平行的性质定理知，选D.答案：D3．若两个平面与第三个平面相交有两条交线且两条交线互相平行，则这两个平面()A．有公共点B．没有公共点C．平行D．平行或相交答案：D4.如图所示，长方体ABCD-A1B1C1D1中，E，F分别是棱AA1和BB1的中点，过EF的平面EFGH分别交BC和AD于G、H，则HG与AB的位置关系是()A．平行B．相交C．异面D．平行和异面解析：因为E，F分别是AA1，BB1的中点，所以EF∥AB.又AB⊄平面EFGH，EF⊂平面EFGH，所以AB∥平面EFGH.又AB⊂平面ABCD，平面ABCD∩平面EFGH＝GH，所以AB∥GH.答案：A5.如图所示，四棱锥P-ABCD中，M，N分别为AC，PC上的点，且MN∥平面PAD，则()A．MN∥PDB．MN∥PAC．MN∥ADD．以上均有可能解析：因为MN∥平面PAD，MN⊂平面PAC，平面PAD∩平面PAC＝PA，所以MN∥PA.答案：B二、填空题6．如图所示，在空间四边形ABCD中，E，F，G，H分别是AB，BC，CD，DA上的点，EH∥FG.则EH与BD的位置关系是______．解析：因为EH∥FG，FG⊂平面BCD，EH⊄平面BCD，所以EH∥平面BCD.因为EH⊂平面ABD，平面ABD∩平面BCD＝BD，所以EH∥BD.答案：平行7.如图所示，正方体ABCD-A1B1C1D1中，AB＝2，点E为AD 的中点，点F在CD上．若EF∥平面AB1C，则线段EF的长度等于________．解析：由于在正方体ABCD-A1B1C1D1中，AB＝2，所以AC＝2 2.又E为AD的中点，EF∥平面AB1C，EF⊂平面ADC，平面ADC∩平面AB1C＝AC，所以EF∥AC，所以F为DC的中点，所以EF＝12AC＝ 2.答案：28．如图，ABCD­A1B1C1D1是正方体，若过A，C，B1三点的平面与底面A1B1C1D1的交线为l，则l与AC的关系是________．解析：因为AC∥面A1B1C1D1，根据线面平行的性质知l∥AC.答案：平行三、解答题9．如图，AB，CD为异面直线，且AB∥α，CD∥α，AC，BD 分别交α于M，N两点，求证AM∶MC＝BN∶ND.证明：连接AD交α于点P，连接MP，NP，因为CD∥α，面ACD∩α＝MP，所以CD∥MP，所以AMMC＝APPD.同理可得NP∥AB，APPD＝BNND，所以AMMC＝BNND.10.如图所示，四面体A-BCD被一平面所截，截面EFGH是一个矩形．(1)求证：CD∥平面EFGH；(2)求异面直线AB、CD所成的角．(1)证明：因为截面EFGH是矩形，所以EF∥GH.又GH⊂平面BCD，EF⊄平面BCD.所以EF⊂平面ACD，平面ACD∩平面BCD＝CD，所以EF∥CD.又EF⊂平面EFGH，CD⊄平面EFGH，所以CD∥平面EFGH.(2)解：由(1)知CD∥EF，同理AB∥FG，由异面直线所成角的定义知，∠EFG即为所求．故AB、CD所成的角为90°.B级能力提升1．下列命题中，正确的命题是()A．若直线a上有无数个点不在平面α内，则a∥αB．若a∥α，则直线a与平面α内任意一条直线都平行C．若a⊂α，则a与α有无数个公共点D．若a⊄α，则a与α没有公共点解析：对于A，直线a与平面α有可能相交，所以A错；对于B，平面α内的直线和直线a可能平行，也可能异面，所以B错；对于D，因为直线a与平面α可能相交，此时有一个公共点，所以D错．答案：C2．对于平面M与平面N，有下列条件：①M、N都垂直于平面Q；②M、N都平行于平面Q；③M内不共线的三点到N的距离相等；④l，m为两条平行直线，且l∥M，m∥N；⑤l，m是异面直线，且l∥M，m∥M；l∥N，m∥N，则可判定平面M与平面N平行的条件是________(填正确结论的序号)．解析：由面面平行的判定定理及性质定理知，只有②⑤能判定M∥N.答案：②⑤3.如图所示，已知P是▱ABCD所在平面外一点，M，N分别是AB，PC的中点，平面PBC∩平面PAD＝l.(1)求证：l∥BC.(2)问：MN与平面PAD是否平行？试证明你的结论．证明：(1)因为BC∥AD，BC⊄平面PAD，AD⊂平面PAD，所以BC∥平面PAD.又BC⊂平面PBC，平面PBC∩平面PAD＝l，所以l∥BC.(2)平行．如图所示，取PD的中点E，连接AE，NE.因为N是PC的中点，所以EN綊12CD.因为M为▱ABCD边AB的中点，所以AM綊12CD.所以EN綊AM，所以四边形AMNE为平行四边形，所以MN∥AE.又MN⊄平面PAD，AE⊂平面PAD，所以MN∥平面PAD.。

2．2.2 直线与平面平行的性质基础梳理练习：如图所示，已知E为空间四边形ABCD的边AB的中点，EF∥平面BCD，求证：F 是AD的中点．证明：因为EF∥平面BCD，BD＝面ABD∩面BCD，所以EF∥BD，因为E为空间四边形ABCD 的边AB的中点，所以F是AD的中点．►思考应用由扣在桌面上的书的实例思考：当一条直线与一个平面平行时，过该直线可作多少个平面与已知平面相交，相交的交线与这条直线又有怎样的位置关系？解析：当一条直线与一个平面平行时，过该直线可作出无数个平面与已知平面相交，这无数条相交直线与这条直线都平行，当然，这无数条交线也互相平行．自测自评1．如果一条直线和一个平面平行，那么这条直线(D)A．只和这个平面内的一条直线平行B．只和这个平面内的两相交直线不相交C．和这个平面内的任何一条直线都平行D．和这个平面内的任何一条直线都不相交解析：因为直线和平面平行，则直线和平面就没有交点，直线和平面内的直线就平行或异面．2．如果a，b是异面直线，且a∥平面α，那么b与α的位置关系是(D)A．b∥αB．b与α相交C．b⊂αD．不确定解析：b与α相交或b⊂α两种情况．3．如果一条直线和一个平面平行，夹在直线和平面间的两线段相等，那么这两条线段所在直线的位置关系是(D)A．平行B．相交C．异面D．不确定4．已知直线l∥平面α，l⊂平面β，α∩β＝m，则直线l，m的位置关系是(A) A．平行B．相交或平行C．相交或异面D．平行或异面基础达标1．直线a∥平面α，平面α内有n条直线交于一点，那么这n条直线中与直线a平行的(B)A．至少有一条B．至多有一条C．有且只有一条D．不可能有解析：直线a与n条直线的交点可确定一个平面，该平面与平面α的交线与a平行，故至多有一条直线与a平行．2．若不在同一直线上的三点A、B、C到平面α的距离相等，则(B)A．平面α∥平面ABCB．△ABC中至少有一边平行于平面αC．△ABC中至多有两边平行于αD．△ABC中只可能有一边与平面α相交解析：若三点在平面α的同侧，则平面α∥平面ABC，有三边平行于α.若一点在平面α的一侧，另两点在平面α的另一侧，则有两边与平面α相交，有一边平行于α，故△ABC中至少有一边平行于平面α.应选B.3．如图，在四面体ABCD中，若截面PQMN是正方形，则在下列命题中，错误的为(C)A．AC⊥BDB．AC∥截面PQMNC．AC＝BDD．异面直线PM与BD所成的角为45°4．在正方体ABCD­A1B1C1D1中，若经过D1B的平面分别交AA1和CC1于点E、F，则四边形D1EBF的形状是(C)A．矩形B．菱形C．平行四边形D．正方形解析：因为平面和左右两个侧面分别交于ED1、BF，所以ED1∥BF，同理D1F∥EB，所以四边形D1EBF是平行四边形．5．a∥β，b∥β，则直线a与b的位置关系：①平行；②垂直不相交；③垂直相交；④不垂直且不相交．其中可能成立的有________．答案：①②③④6．已知直线a，b，平面α，且a∥b，a∥α，a，b都在平面α外，求证：b∥α.证明：过a作平面β，使它与平面α相交，交线为c，∵a∥α，a⊂β，a⊄α，α∩β＝c，∴a∥c.∵a∥b，∴b∥c.又∵c⊂α，b⊄α，∴b∥α.巩固提升7．E，H分别是空间四边形ABCD的边AB，AD的中点，平面α过EH分别交BC，CD于F，G.求证：EH∥FG.证明：连接EH.∵E，H分别是AB，AD的中点，∴EH∥BD.又BD⊂平面BCD，EH⊄平面BCD，∴EH∥平面BCD.又EH⊂平面α，平面α∩平面BCD＝FG，∴EH∥FG.8．如图所示，一平面与空间四边形ABCD的对角线AC，BD都平行，且交空间四边形的边AB，BC，CD，DA分别于E，F，G，H.(1)求证：EFGH为平行四边形；(2)若AC＝BD，四边形EFGH能否为菱形？(3)在什么情况下，四边形EFGH为矩形？(4)在什么情况下，四边形EFGH为正方形？解析：(1)证明：∵BD∥平面EFGH，BD⊂平面ABD，平面ABD∩平面EFGH＝EH，∴BD∥EH，同理BD∥FG.∴EH∥FG，同理EF∥HG.∴四边形EFGH为平行四边形．(2)四边形EFGH为菱形．(3)当AC⊥BD时，四边形EFGH为矩形．(4)当AC⊥BD，AC＝BD，且E，F，G，H分别是AB，BC，CD，AD的中点时，四边形EFGH 为正方形．1．直线和平面平行的性质定理揭示了线面平行中蕴涵着线线平行，通过线面平行可得线线平行，也给出了作平行线的重要方法．2．注意线线平行与线面平行的相互转化．。

直线与平面平行的性质．平面与平面平行的性质一、选择题(本大题共小题，每小题分，共分)．如果，是两条异面直线，且∥α，那么与α的位置关系是( )．∥α．与α相交．⊂α．不确定．如果平面α平行于平面β，那么( )．平面α内任意直线都平行于平面β．平面α内仅有两条相交直线平行于平面β．平面α内任意直线都平行于平面β内的任意直线．平面α内的直线与平面β内的直线不能垂直．在正方体­′′′′中，下列四对截面中，彼此平行的一对截面是( )．平面′与平面′′．平面′′与平面′．平面′′与平面′．平面′′与平面′图--．如图--所示，正方体的底面与正四面体的底面在同一平面α上，且∥，正方体的六个面所在的平面与直线，相交的平面个数分别记为，，那么＋＝( ) ．．．．．下面给出四个命题，其中正确命题的个数是( )①若∥α，∥α，则∥；②若∥α，⊂α，则∥；③若∥，⊂α，则∥α；④若∥，∥α，则∥α.．．．．．若，为两条不重合的直线，α，β为两个不重合的平面，则下列命题中正确的是( ) ．若，都平行于平面α，则，一定不是相交直线．若，都垂直于平面α，则，一定是平行直线．已知α，β互相平行，，互相平行，若∥α，则∥β．若，在平面α内的射影互相平行，则，互相平行图--．如图--所示，在正方体-中，，分别为棱，的中点，在平面内且与平面平行的直线( ) ．不存在．有条．有条．有无数条二、填空题(本大题共小题，每小题分，共分)．已知α，β，γ是三个不重合的平面，，是两条不重合的直线．若α∩β＝，β∩γ＝，且α∥γ，则与的位置关系是.．已知，，是互不相同的直线，α，β，γ是三个不同的平面，给出下列命题：①若与为异面直线，⊂α，⊂β，则α∥β；②若α∥β，⊂α，⊂β，则∥；③若α∩β＝，β∩γ＝，γ∩α＝，∥γ，则∥.其中所有真命题的序号为．．如图--甲所示，往透明塑料制成的长方体-容器内灌进一些水，固定容器底面一边于地面上，再将容器倾斜，随着倾斜度的不同，有下列四种说法：①水的部分始终呈棱柱状；②水面四边形的面积不变；③棱始终与水面平行；④当容器倾斜到如图--乙所示位置时，·是定值.其中所有正确说法的序号是．图--．有一木块如图--所示，点在平面′′内，棱平行于平面′′，要经过点和棱将木块锯开，锯开的面必须平整，有种锯法，则＝．图--三、解答题(本大题共小题，共分)．(分)如图--①所示，在直角梯形中，∥，⊥，＝＝，为的中点，，，分别为，，的中点，。

第二章点、直线、平面之间的位置关系2.2 直线、平面平行的判定及其性质2.2.3 直线与平面平行的性质A级基础巩固一、选择题1．已知直线l∥平面α，P∈α，那么过点P且平行于l的直线()A．只有一条，不在平面α内B．只有一条，在平面α内C．有两条，不一定都在平面α内D．有无数条，不一定都在平面α内解析：如图所示，因为l∥平面α，P∈α，所以直线l与点P确定一个平面β，α∩β＝m，所以P∈m，所以l∥m且m是唯一的．答案：B2．如果l∥平面α，则l平行于α内()A．全部直线B．唯一确定的直线C．任一直线D．过l的平面与α的交线解析：利用线面平行的性质定理知，选D.答案：D3．若两个平面与第三个平面相交有两条交线且两条交线互相平行，则这两个平面()A．有公共点B．没有公共点C．平行D．平行或相交答案：D4.如图所示，长方体ABCD-A1B1C1D1中，E，F分别是棱AA1和BB1的中点，过EF的平面EFGH分别交BC和AD于G、H，则HG与AB的位置关系是()A．平行B．相交C．异面D．平行和异面解析：因为E，F分别是AA1，BB1的中点，所以EF∥AB.又AB⊄平面EFGH，EF⊂平面EFGH，所以AB∥平面EFGH.又AB⊂平面ABCD，平面ABCD∩平面EFGH＝GH，所以AB∥GH.答案：A5.如图所示，四棱锥P-ABCD中，M，N分别为AC，PC上的点，且MN∥平面PAD，则()A．MN∥PDB．MN∥PAC．MN∥ADD．以上均有可能解析：因为MN∥平面PAD，MN⊂平面PAC，平面PAD∩平面PAC＝PA，所以MN∥PA.答案：B二、填空题6．如图所示，在空间四边形ABCD中，E，F，G，H分别是AB，BC，CD，DA上的点，EH∥FG.则EH与BD的位置关系是______．解析：因为EH∥FG，FG⊂平面BCD，EH⊄平面BCD，所以EH∥平面BCD.因为EH⊂平面ABD，平面ABD∩平面BCD＝BD，所以EH∥BD.答案：平行7.如图所示，正方体ABCD-A1B1C1D1中，AB＝2，点E为AD 的中点，点F在CD上．若EF∥平面AB1C，则线段EF的长度等于________．解析：由于在正方体ABCD-A1B1C1D1中，AB＝2，所以AC＝2 2.又E为AD的中点，EF∥平面AB1C，EF⊂平面ADC，平面ADC∩平面AB1C＝AC，所以EF∥AC，所以F为DC的中点，所以EF＝12AC＝ 2.答案：28．如图，ABCD­A1B1C1D1是正方体，若过A，C，B1三点的平面与底面A1B1C1D1的交线为l，则l与AC的关系是________．解析：因为AC∥面A1B1C1D1，根据线面平行的性质知l∥AC.答案：平行三、解答题9．如图，AB，CD为异面直线，且AB∥α，CD∥α，AC，BD 分别交α于M，N两点，求证AM∶MC＝BN∶ND.证明：连接AD交α于点P，连接MP，NP，因为CD∥α，面ACD∩α＝MP，所以CD ∥MP ，所以AM MC ＝APPD .同理可得NP ∥AB ，AP PD ＝BNND ，所以AM MC ＝BN ND.10.如图所示，四面体A -BCD 被一平面所截，截面EFGH 是一个矩形．(1)求证：CD ∥平面EFGH ； (2)求异面直线AB 、CD 所成的角． (1)证明：因为截面EFGH 是矩形， 所以EF ∥GH .又GH ⊂平面BCD ，EF ⊄平面BCD .所以EF ⊂平面ACD ，平面ACD ∩平面BCD ＝CD ，所以EF ∥CD . 又EF ⊂平面EFGH ，CD ⊄平面EFGH ， 所以CD ∥平面EFGH .(2)解：由(1)知CD ∥EF ，同理AB ∥FG ，由异面直线所成角的定义知，∠EFG 即为所求．故AB 、CD 所成的角为90°.B 级 能力提升1．下列命题中，正确的命题是()A．若直线a上有无数个点不在平面α内，则a∥αB．若a∥α，则直线a与平面α内任意一条直线都平行C．若a⊂α，则a与α有无数个公共点D．若a⊄α，则a与α没有公共点解析：对于A，直线a与平面α有可能相交，所以A错；对于B，平面α内的直线和直线a可能平行，也可能异面，所以B错；对于D，因为直线a与平面α可能相交，此时有一个公共点，所以D错．答案：C2．对于平面M与平面N，有下列条件：①M、N都垂直于平面Q；②M、N都平行于平面Q；③M内不共线的三点到N的距离相等；④l，m为两条平行直线，且l∥M，m∥N；⑤l，m是异面直线，且l∥M，m∥M；l∥N，m∥N，则可判定平面M与平面N平行的条件是________(填正确结论的序号)．解析：由面面平行的判定定理及性质定理知，只有②⑤能判定M∥N.答案：②⑤3.如图所示，已知P是▱ABCD所在平面外一点，M，N分别是AB，PC的中点，平面PBC∩平面PAD＝l.(1)求证：l∥BC.(2)问：MN与平面PAD是否平行？试证明你的结论．证明：(1)因为BC∥AD，BC⊄平面PAD，AD⊂平面PAD，所以BC∥平面PAD.又BC⊂平面PBC，平面PBC∩平面PAD＝l，所以l∥BC.(2)平行．如图所示，取PD的中点E，连接AE，NE.因为N是PC的中点，所以EN綊12CD.因为M为▱ABCD边AB的中点，所以AM綊12CD.所以EN綊AM，所以四边形AMNE为平行四边形，所以MN∥AE.又MN⊄平面PAD，AE⊂平面PAD，所以MN∥平面PAD.。

2.2直线、平面平行的判定及其性质2.2.1直线与平面平行的判定2.2.2平面与平面平行的判定一、基础达标1．已知三个平面α，β，γ，一条直线l，要得到α∥β，必须满足下列条件中的() A．l∥α，l∥β，且l∥γB．l?γ，且l∥α，l∥βC．α∥γ，且β∥γD．l与α，β所成的角相等答案 C解析α∥γ?α与γ无公共点β∥γ?β与γ无公共点?α与β无公共点?α∥β.2．下列图形中能正确表示语句“平面α∩β＝l，a?α，b?β，a∥β”的是()答案 D解析A中不能正确表达b?β；B中不能正确表达a∥β；C中也不能正确表达a∥β.D正确．3．(2014·郑州高一检测)在正方体ABCD－A1B1C1D1中，M是棱CD上的动点，则直线MC1与平面AA1B1B的位置关系是() A．相交B．平行C．异面D．相交或平行答案 B解析如图，MC1?平面DD1C1C，而平面AA1B1B∥平面DD1C1C，故MC1∥平面AA1B1B.4．平面α内有不共线的三点到平面β的距离相等且不为零，则α与β的位置关系为() A．平行B．相交C．平行或相交D．可能重合答案 C解析若三点分布于平面β的同侧，则α与β平行，若三点分布于平面β的两侧，则α与β相交．5．点E，F，G，H分别是空间四边形ABCD的边AB，BC，CD，DA的中点，则空间四面体的六条棱中与平面EFGH平行的条数是() A．0 B．1C．2 D．3答案 C解析如图，由线面平行的判定定理可知，BD∥平面EFGH，AC∥平面EFGH.6．若夹在两个平面间的三条平行线段相等，那么这两个平面的位置关系为________．答案平行或相交解析三条平行线段共面时，两平面可能平行也可能相交，当三条平行线段不共面时，两平面一定平行．7.如图，在底面是矩形的四棱锥P－ABCD中，E、F分别是PC、PD的中点，求证：EF∥平面PAB.证明∵E、F分别是PC，PD的中点，∴EF∥CD，∵CD∥AB，∴EF∥AB，∵EF?面PAB，AB?平面PAB，∴EF∥平面P AB.二、能力提升8．(2014·绍兴高一检测)已知直线l，m，平面α，β，下列命题正确的是() A．l∥β，l?α?α∥βB．l∥β，m∥β，l?α，m?α?α∥βC．l∥m，l?α，m?β?α∥βD．l∥β，m∥β，l?α，m?α，l∩m＝M?α∥β答案 D解析如图所示，在长方体ABCD－A1B1C1D1中，AB∥CD，则AB∥平面DC1，AB?平面AC，但是平面AC与平面DC1不平行，所以A错误；取BB1的中点E，CC1的中点F，则可证EF∥平面AC，B1C1∥平面AC.EF?平面BC1，B1C1?平面BC1，但是平面AC与平面BC1不平行，所以B错误；可证AD∥B1C1，AD?平面AC，B1C1?平面BC1，又平面AC与平面BC1不平行，所以C错误；很明显D是面面平行的判定定理，所以D正确．9．三棱锥S－ABC中，G为△ABC的重心，E在棱SA上，且AE＝2ES，则EG 与平面SBC的关系为________．答案平行解析如图，延长AG交BC于F，则由G为△ABC的重心知AG∶GF＝2，又AE∶ES＝2，∴EG∥SF，又SF?面SBC，EG?平面SBC，∴EG∥平面SBC.10．如图是正方体的平面展开图．在这个正方体中，①BM∥平面DE；②CN∥平面AF；③平面BDM∥平面AFN；④平面BDE∥平面NCF.以上四个命题中，正确命题的序号是________．答案①②③④解析以ABCD为下底面还原正方体，如图：则易判定四个命题都是正确的．11．(2014·自贡高一检测)如图，在三棱柱ABC－A1B1C1中，D为BC的中点，连接AD，DC1，A1B，AC1，求证：A1B∥平面ADC1.证明连接A1C，设A1C∩AC1＝O，再连接OD.由题意知，A1ACC1是平行四边形，所以O是A1C的中点，又D是CB的中点，因此OD是△A1CB的中位线，即OD∥A1B.又A1B?平面ADC1，OD?平面ADC1，所以A1B∥平面ADC1.三、探究与创新12.如图在正方体ABCD－A1B1C1D1中，E，F，M，N分别为棱AB，CC1，AA1，C1D1的中点．求证：平面CEM∥平面BFN.证明因为E，F，M，N分别为其所在各棱的中点，如图连接CD1，A1B，易知FN∥CD1.同理，ME∥A1B.易证四边形A1BCD1为平行四边形，所以ME∥NF.连接MD1，同理可得MD1∥BF.又BF，NF为平面BFN中两相交直线，ME，MD1为平面CEM中两相交直线，故平面CEM∥平面BFN.13.如图所示，在正方体ABCD－A1B1C1D1中，E、F、G、H分别是棱CC1、C1D1、D1D、CD的中点，N是BC的中点，点M在四边形EFGH及其内部运动，则M满足什么条件时，有MN∥平面B1BDD1.(不必考虑所有可能情况，只要写出一个即可，并说明理由)解①若M为H点时，连接HN，∵H、N为边DC，BC中点，∴HN∥BD.∵BD?平面BDD1B1，HN?平面BDD1B1，∴HN∥平面B1BDD1，即MN∥平面B1BDD1.②若M为F点时，取BD中点P，连接PN、FN、D1P，∵N为BC中点，F为D1C1中点，结合中位线及正方体的性质可知PN綉D1F，∴四边形D1PNF为平行四边形，∴FN∥D1P，∵FN?平面B1BDD1，D1P?平面B1BDD1，∴FN∥平面B1BDD1，即MN∥平面B1BDD1.③连接FH，若M为FH上任一点，作MQ∥D1C1交D1D于点Q，取BD中点P，并连接PQ，PN，易知MQPN为平行四边形，∴MN∥PQ，∵MN?平面B1BDD1，PQ?平面B1BDD1，∴MN∥平面B1BDD1.综上知M在线段FH上时，MN∥平面B1BDD1.。

实用文档
2021年高中数学 2.2.3 直线与平面平行的性质课时练 新人教A 版必修2
一、选择题:
1. 表示直线， 表示平面，可以确定 的条件是（ ）.
A. B.
C. D. 的夹角相等
2.已知直线，为平面内任一直线，则直线与直线的位置关系是（ ）
A ．平行
B ．异面
C ．相交
D ．平行或异面
3．梯形中，，，，则直线与平面内的直线的位置关系是（ ）
A ．平行
B ．平行或异面
C ．平行或相交
D ．相交或异面
4.已知如下图（左），直线是过正方体的顶点的平面与下底面所在平面的交线，则下列结论错误的是（ ）
A. B. C ． D.
二、填空题:
5．若直线均平行于平面，则直线的位置关系是____________________.
6.已知如上图（右），正方体的棱长为1，点是面的中心，点是面的对角线上一点，且，则线段的长为__________.
三、解答题：
7.如图,空间四边形被一个平面所截,截面是平行四边形.
求证:
8.如图，空间四边形的对棱、成的角，且，平行于与的截面分别交、、、于、、、．
（１）求证：四边形为平行四边形；（２）在的何处时截面的面积最大？最大面积是多少？
9.如图，在所在平面外有一点P ，D、E 分别是PB与AB上的点,过D, E 作平面平行于BC ，试画出这个平面与其它各面的交线，并说明画法的依据.
10. 如图，在四棱锥中，是平行四边形，，分别是，的中点．
求证：平面． 26157 662D 昭22863 594F 奏H{24371 5F33 弳22139 567B 噻
实用文档。

2-2-3直线与平面平行的性质一、选择题1．已知直线a、b、c及平面α，下列哪个条件能确定a∥bA．a∥α，b∥αB．a⊥c，b⊥cC．a、b与c成等角D．a∥c，b∥c2．正方体ABCD－A1B1C1D1中，截面BA1C1与直线AC的位置关系是A．AC∥截面BA1C1B．AC与截面BA1C1相交C．AC在截面BA1C1内D．以上答案都错误3．已知直线∥平面α，⊂平面β，α∩β＝m，则直线，m的位置关系是A．相交B．平行C．异面D．相交或异面4．已知直线m∥直线n，直线m∥平面α，过m的平面β与α相交于直线a，则n与a 的位置关系是A．平行B．相交C．异面D．以上均有可能5．设a，b是两条直线，α，β是两个平面，若a∥α，a⊂β，α∩β＝b，则α内与b相交的直线与a的位置关系是A．平行B．相交C．异面D．平行或异面6．如图所示的三棱柱ABC－A1B1C1中，过A1B1的平面与平面ABC交于直线DE，则DE与AB的位置关系是A．异面B．平行C．相交D．以上均有可能7．直线a∥平面α，α内有n条直线交于一点，则这n条直线中与直线a平行的直线A．至少有一条B．至多有一条C．有且只有一条D．没有8．如图所示，在空间四边形ABCD中，E，F，G，H分别是AB，BC，CD，DA上的点，EH ∥FG，则EH与BD的位置关系是A．平行B．相交C．异面D．不确定9．一平面截空间四边形的四边得到四个交点，如果该空间四边形只有一条对角线与这个截面平行，那么这四个交点围成的四边形是A．梯形B．菱形C．平行四边形D．任意四边形10．已知正方体AC1的棱长为1，点1C1C1C，BD＝n，当EFGH是菱形时，错误!＝________三、解答题15．求证，如果一条直线和两个相交平面平行，那么该直线与相交平面的交线平行．[分析] 写出已知、求证，画出图形．由于图形比较单一，要添加辅助平面，利用线面平行性质定理先得线线平行，再由平行公理证明．[解析] 已知：a∥α，a∥β，且α∩β＝b求证：a∥b16．如图，已知A，B，C，D四点不共面，且AB∥平面α，CD∥平面α，AC∩α＝E，AD∩α＝F，BD∩α＝H，BC∩α＝G求证：EFHG是一个平行四边形．17．如下图，在长方体ABCD－A1B1C1D1中，E、H分别是棱A1B1、D1C1上的点，且EH∥A1D1，过EH的平面与棱BB1，CC1相交，交点分别为F、G求证：FG∥平面ADD1A118．四棱锥1C1C1C4[答案] A[解析] ∵m∥α，α∩β＝a，m⊂β，∴m∥∥n，∴n∥a5[答案] C[解析] ∵a∥α，a⊂β，α⊂β＝b，∴a∥b∴α内与b相交的直线与a异面．6[答案] B[解析] ∵A1B1∥AB，AB⊂平面ABC，A1B1⊄ABC，∴A1B1∥平面ABC又A1B1⊂平面A1B1ED，平面A1B1ED∩平面ABC＝DE，∴DE∥A1B1又AB∥A1B1，∴DE∥AB7[答案] B[解析] 设这n条直线的交点为[解析] 错误!＝错误!＝错误!＝错误!，而EF＝FG15证明：如图，在平面α上任取一点A，且使A∉b∵a∥α，∴A∉a故点A和直线a确定一个平面γ，设γ∩α＝m同理，在平面β上任取一点B，且使B∉b，则B和a确定平面δ，设δ∩β＝n∵a∥α，a⊂γ，γ∩α＝m，∴a∥m同理a∥n，则m∥n又m⊄β，n⊂β，∴m∥β又∵m⊂α，α∩β＝b，∴m∥∥m，∴a∥b[点评] 本题利用线面平行的判定和性质定理，完成了平面问题和空间问题的相互转化．转化的思想是一种重要的数学思想．本节常用的转化为：错误!错误!错误!错误!错误!16[证明] ∵AB∥α，平面ABC∩α＝EG，AB⊂平面ABC，∴EG∥AB同理，FH∥AB，∴EG∥FH同理，EF∥GH∴四边形EFHG是一个平行四边形．17[证明] ∵EH∥A1D1，又A1D1∥B1C1∴EH∥B1C1∴EH∥平面BCC1B1又平面EHGF∩平面BCC1B1＝FG∴EH∥FG∴FG∥A1D1又FG⊄平面ADD1A，A1D1⊂平面ADD1A1，∴FG∥平面ADD1A118[解析] 在PC上取点E，使错误!＝错误!，则BE∥平面PAD证明如下：延长DA和CB交于点F，连接PF 梯形ABCD中，AB∥CD，AB＝错误!CD∴错误!＝错误!＝错误!，∴错误!＝错误!又错误!＝错误!，∴△PFC中，错误!＝错误!，∴BE∥PF，而BE⊄平面PAD，PF⊂平面PAD∴BE∥平面PAD。