张量分析1

张量分析张量分析，又称张量微积分，是一门研究多维空间中的向量和张量的数学工具。

它在物理学、工程学、计算机科学等领域有着广泛的应用。

张量分析的核心思想是通过张量的计算和运算，来描述和解释多维空间中的现象和问题。

在数学中，张量是一种广义的向量概念。

它不仅可以表示标量和向量，还可以表示具有更高维度的物理量。

例如，二阶张量可以表示物体的形变和应力分布，三阶张量可以表示电磁场的分布，四阶张量可以表示弹性材料的性质等。

张量分析的基本概念包括张量的定义和表示、张量的变换规律以及张量的运算。

对于二阶张量，可以用一个矩阵来表示。

张量的变换规律与坐标系的选择有关，不同的坐标系下，同一个张量可以表示为不同的矩阵形式。

张量的运算包括加法、数乘、内积和外积等。

这些运算在物理和工程问题中具有重要的意义，可以帮助研究人员推导和解决实际问题。

在物理学中，张量分析被广泛应用于描述和分析物体的运动、形变、应力等问题。

例如，通过分析物体的应力张量，可以判断物体是否会发生破坏或变形。

在工程学中，张量分析可以用于解决弹性力学、流体力学、电磁学等问题。

在计算机科学中，张量分析可以用于图像处理、模式识别等领域。

张量分析的发展离不开数学家们的努力。

早在19世纪，克里斯托弗·亚当斯（Christopher Adams）就提出了张量的概念。

20世纪初，爱因斯坦在相对论的研究中也广泛应用了张量分析。

随着计算机的发展和计算能力的提高，张量分析在科学研究中的应用也越来越广泛。

虽然张量分析在各个领域中都有广泛的应用，但它的理论和方法并不容易掌握。

要学好张量分析，需要对线性代数、微积分和向量分析等数学知识有扎实的掌握。

此外，也需要具备一定的物理学和工程学的基础知识。

对于初学者来说，可以通过学习相关的教材和参考资料，同时结合实际问题进行练习和应用。

总之，张量分析是一门重要的数学工具，对于描述和解决多维空间中的问题具有重要的意义。

它在物理学、工程学、计算机科学等领域有着广泛的应用。

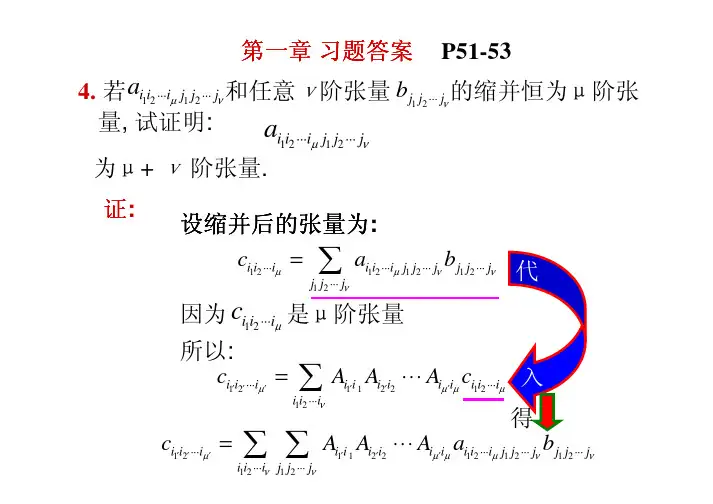
张量分析总结[范文]第一篇：张量分析总结[范文]中国矿业大学《张量分析》课程总结报告第 1 页一、知识总结张量概念1.1 指标记法哑标和自由指标的定义及性质自由指标：在每一项中只出现一次，一个公式中必须相同。

性质：在表达式或方程中自由指标可以出现多次，但不得在同项内重复出现两次。

哑标：一个单项式内，在上标（向量指标）和下标（余向量指标）中各出现且仅出现一次的指标。

性质：哑标可以把多项式缩写成一项；自由指标可以把多个方程缩写成一个方程。

例：A11x1+A12x2+A13x3=B1A21x1+A22x2+A23x3=B2 A31x1+A32x2+A33x3=B3式(1.1)可简单的表示为下式：(1.1)Aijxj=Bi(1.2)其中：i为自由指标，j为哑标。

特别区分，自由指标在同一项中最多出现一次，表示许多方程写成一个方程；而哑标j则在同项中可出现两次，表示遍历求和。

在表达式或者方程中自由指标可以出现多次，但不得在同项中出现两次。

1.2 Kronecker符号定义δij为：δij=⎨⎧1,i=j0,i≠j⎩(1.3)δij的矩阵形式为：⎡100⎤⎥δij=⎢010⎢⎥⎢⎣001⎥⎦(1.4)可知δijδij=δii=δjj=3。

δ符号的两指标中有一个与同项中其它因子的指标相同时，可把该因子的重指标换成δ的另一个指标，而δ符号消失。

如：δijδjk=δikδijδjkδkl=δil(1.5)中国矿业大学《张量分析》课程总结报告第 2 页δij的作用：更换指标、选择求和。

1.3 Ricci符号为了运算的方便，定义Ricci符号或称置换符号：⎧1,i,j,k为偶排列⎪lijk=⎨-1,i,j,k为奇排列⎪0,其余情况⎩(1.6)图1.1 i,j,k排列图lijk的值中，有3个为1，3个为-1，其余为0。

Ricci符号（置换符号）是与任何坐标系都无关的一个符号，它不是张量。

1.4 坐标转换图1.2 坐标转换如上图所示，设旧坐标系的基矢为ei，新坐标系的基矢为ei'。

第一章 张量的概念§ 1.1 引言什么是张量？这是读者在开始学习本课程时会提出的问题，现从读者已有的力学知识出发，举例对这个问题作一些初步的阐述，使读者对张量这个新的概念，有个初步的理解。

有三维空间，一个矢量（例如力矢量、速度矢量等）在某些参考坐标系中，有三个分量，这三个分量的集合，规定了这个矢量。

当坐标变化换时 ，这些分量按一定的变换法则变换。

在力学中还有一些更复杂的量。

例如受力物体内一点的应力状态，有9个应力分量，如以直角坐标表示，用矩阵形式列出，则有()⎪⎪⎪⎭⎫⎝⎛σσσσσσσσσ=σzz zyzxyz yy yxxz xy xx ij 这9个分量的集合，规定了一点的应力状态，称为应力张量。

当坐标变换时，应力张量的分量按一定的变换法则变换，再如，一点的应力状态，具有和应力张量相似的性质，称为应变张量。

把上述的力矢量、速度矢量、应力张量、应变张量等量的性质抽象化，撇开它们所表示的量的物理性质，抽出其数学上的共性，便得出抽象的张量概念。

所谓张量是一个物理量或几何量，它由在某参考坐标系中一定数目的分量的集合所规定，当坐标变换时，这些分量按一定的变换法则变换。

张量有不同的“阶”和“结构”，这由它们所遵循的不同的变换法则来区分。

矢量是一阶张量；应力张量、应变张量是二阶张量；还有三阶、四阶、......等高阶张量。

可以看出，张量是矢量概念的推广。

关于张量的严密的解析定义，将在 § 1.8中讨论。

由张量的特性可以看出，它是一种不依赖于特定坐标系的表达物理定律的方式。

采用张量记法表示的方程，在某一坐标系中成立，则在容许变换的其它坐标系中也成立，即张量方程具有不变性。

这使它特别适合于表达物理定律，因为物理定律与人们为了描述它所采用的坐标系无关。

因此，张量分析为人们提供了推导基本方程的有力工具。

此外，张量记法简洁，是一种非常精炼的数学语言。

张量这个名词是沃伊特（V oigt ）首先提出的，用来表示晶体的应力（张力）状态，可见张量分析与弹性力学关系的密切。

张量分析习题答案张量分析习题答案张量分析是数学中的一个重要分支，它在物理学、工程学和计算机科学等领域中有着广泛的应用。

学习张量分析需要掌握一定的数学知识和技巧，通过解答习题可以更好地理解和应用这一理论。

本文将给出一些张量分析习题的详细解答，帮助读者更好地掌握这一领域的知识。

1. 习题一：设有一个二阶张量A，其分量为Aij = 2i + j，求A的迹和对称部分。

解答：首先，迹是指一个方阵的主对角线上元素的和。

对于二阶张量A，其迹为Aii，即A的两个主对角线元素之和。

根据题目给出的分量表达式，可以得到A的迹为A11 + A22 = 2(1) + 1 + 2(2) + 2 = 9。

其次，对称部分是指一个张量的分量满足Aij = Aji的部分。

对于二阶张量A，其对称部分为(A + A^T)/2，其中A^T表示A的转置。

根据题目给出的分量表达式，可以得到A的转置矩阵为：A^T = [A11 A21][A12 A22]= [2(1) + 1 2(2) + 2][1 2]将A和A^T代入对称部分的表达式中，可以得到对称部分为：(A + A^T)/2 = [(2(1) + 1) + (2(1) + 1)]/2 [(2(2) + 2) + 2]/2[(1 + 1) + 1]/2 [(2 + 2) + 2]/2[3 4][1 2]2. 习题二：设有一个三阶张量B，其分量为Bijk = i^2 + j^2 + k^2，求B的迹和对称部分。

解答：对于三阶张量B，其迹为Biii，即B的三个主对角线元素之和。

根据题目给出的分量表达式，可以得到B的迹为B111 + B222 + B333 = (1^2 + 1^2 + 1^2) + (2^2 + 2^2 + 2^2) + (3^2 + 3^2 + 3^2) = 9 + 12 + 27 = 48。

对于三阶张量B，其对称部分为(B + B^T)/2，其中B^T表示B的转置。

根据题目给出的分量表达式，可以得到B的转置张量为：B^T = [B111 B211 B311][B121 B221 B321][B131 B231 B331]= [1^2 + 1^2 + 1^2 2^2 + 1^2 + 1^2 3^2 + 1^2 + 1^2][1^2 + 2^2 + 1^2 2^2 + 2^2 + 1^2 3^2 + 2^2 + 1^2][1^2 + 3^2 + 1^2 2^2 + 3^2 + 1^2 3^2 + 3^2 + 1^2]= [3 6 9][6 9 14][9 14 19]将B和B^T代入对称部分的表达式中，可以得到对称部分为：(B + B^T)/2 = [(1^2 + 1^2 + 1^2) + (3)]/2 [(2^2 + 1^2 + 1^2) + (6)]/2 [(3^2 + 1^2 + 1^2) + (9)]/2[(1^2 + 2^2 + 1^2) + (6)]/2 [(2^2 + 2^2 + 1^2) + (9)]/2 [(3^2 + 2^2 +1^2) + (14)]/2[(1^2 + 3^2 + 1^2) + (9)]/2 [(2^2 + 3^2 + 1^2) + (14)]/2 [(3^2 + 3^2 + 1^2) + (19)]/2[5 8 10][8 11 16][10 16 24]通过以上习题的解答，我们可以更好地理解和应用张量分析的知识。

附录I 张量分析近代力学在电子计算机的辅助下冲破了数学求解上的重重困难，取得了突飞猛进的发展，力求对复杂的物理现象和工程问题做出更为系统和真实的描述和研究。

张量分析能以简洁的表达形式和清晰的推导过程来有效地描述复杂问题的本质，已被近代力学文献和教科书普遍采用。

作为入门，此处着重介绍笛卡儿坐标系和正交曲线坐标系中的张量。

I.1 矢量和张量的记法，求和约定力学中常用的量可以分成三类：只有大小没有方向性的物理量称为标量。

例如温度T 、密度ρ、时间t 等。

既有大小又有方向性的物理量称为矢量，常用黑体（或加箭头）表示，为与课堂讲述一致，此处选择用上加箭头表示矢量。

例如矢径r 、位移u 、速度v 、力f 等。

具有多重方向性的更为复杂的物理量称为张量，常用黑体（或加下横）表示，为与课堂讲述一致，此处选择用下加横线表示矢量。

例如一点的应力状态要用应力张量来表示，它是具有二重方向性的二阶张量，记为σ。

矢量可以在参考坐标系中分解。

例如图1 中P 点的位移u 在笛卡儿坐标系()321,,x x x 中分解为∑==++=31332211i i i e u e u e u e u u (I.1)其中1u 、2u 、3u 是位移的三个分量，1e 、2e 、3e是沿坐标轴的三个单位基矢量。

由此引出矢量（可推广至张量）的三种记法： ( l ）实体记法：把矢量或张量的整个物理实体用一个黑体字母或上加箭头来表示。

例如把位移记为u 。

( 2 ）分解式记法：同时写出矢量或张量的分量和相应分解方向的基矢量。

例如用式(I.1)表示位移u 。

( 3 ）分量记法：把矢量或张量用其全部分量的集合来表示，省略相应的基矢量。

例如用三个位移分量()3,2,1=i u i 的集合表示位移u 。

下面详细讨论后两种记法中广泛采用的指标符号。

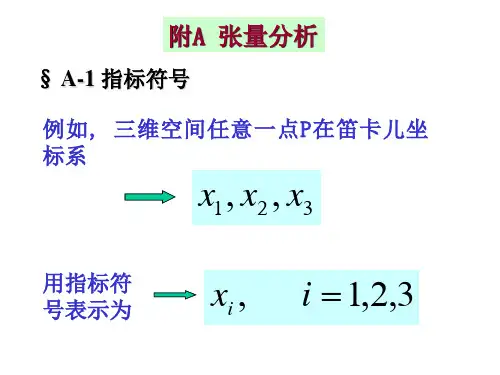
对于一组性质相关的n 个量可以采用指标符号来表示。

例如，n 维空间中矢量a 的n 个分量1a ，2a ，…，n a 可缩写成()n i a i ,,2,1 =。

一 爱因斯坦求和约定1.1指标变量的集合：n n y y y x x x ,...,,,...,,2121表示为：n j y n i x j i ...,3,2,1,,...,3,2,1,==写在字符右下角的 指标，例如xi 中的i 称为下标。

写在字符右上角的指标，例如yj 中的j 称为上标；使用上标或下标的涵义是不同的。

用作下标或上标的拉丁字母或希腊字母，除非作了说明，一般取从1到n 的所有整数，其中n 称为指标的范围。

1.2求和约定若在一项中，同一个指标字母在上标和下标中重复出现，则表示要对这个指标遍历其范围1，2，3，…n 求和。

这是一个约定，称为求和约定。

例如：333323213123232221211313212111bx A x A x A b x A x A x A bx A x A x A =++=++=++筒写为：ijijbx A =ｊ——哑指标ｉ——自由指标，在每一项中只出现一次，一个公式中必须相同遍历指标的范围求和的重复指标称为“哑标”或“伪标”。

不求和的指标称为自由指标。

1.3 Kronecker-δ符号（克罗内克符号）和置换符号Kronecker-δ符号定义j i ji ij ji ≠=⎩⎨⎧==当当01δδ置换符号ijkijk e e =定义为:⎪⎩⎪⎨⎧-==的任意二个指标任意k j,i,当021)(213,132,3的奇置换3，2，1是k j,i,当112)(123,231,3的偶置换3，2，1是k j,i,当1ijk ijke ei,j,k 的这些排列分别叫做循环排列、逆循环排列和非循环排列。

置换符号主要可用来展开三阶行列式：231231331221233211231231133221332211333231232221131211a a a a a a a a a a a a a a a a a a a a a a a a a a a a ---++==因此有：ijmjimii i i jijAA aa a a a ==++=δδδδδ332211kijjkiijkkjiikjjikijkee e e e e e ==-=-=-=同时有：ijjijij iiiijijijkj ikilkljkijjjiiijijijkjikiie e aa aa a a a aa δδδδδδδδδδδδδδδδδδδ=⋅=++=========++=332211332211331001010100131211232221333231321333222111321321321-=====δδδδδδδδδδδδδδδδδδδδδδδδδδδe e k j i k j i k j i k k k j j j i i i ijk333222111321321321r q p r q p r q p k k k j j j i i i pqr ijke e δδδδδδδδδδδδδδδδδδ⋅=ipp i p i p i p i δδδδδδδδδ==++11332211krkqkpjrjqjpiriqippqrijke e δδδδδδδδδ=jqirjriqjrjqiriqkqrijke e kp δδδδδδδδ-===321321322311332112312213322113312312332211333231232221131211k j i ijkkjiijkaa a e a a a e aa a a a a a a a a a a a a a a a a aaaa a aaa a A ==---++==Kronecker-δ和置换符号符号的关系为：itjsjtiskstkije e δδδδ-=二 张量代数2.1张量的加法(减法)两个同阶、同变异(结构) 的张量可以相加(或相减)。

第一篇 张量分析第一章 矢 量 §1—1 矢量表示法物理中的位移、速度、力都是矢量。

利用三维空间中的有向线段ν表示矢量是最直观的表示法，如图1-1所示。

有向线段的长度v 代表矢量的大小。

这种方法不依赖于坐标系的选择。

矢量的分量表示法是另一种表示方法，选定一个坐标系。

比如通常的正交直线坐标系，即卡氏坐标系，然后确定矢量对于该坐标系的分量(,,)x y z v v v ν(1-1a)这一有序数也可视作一个单行矩阵。

矢量也可以用基矢与其对应分量写成x y z iv jv kv ν=++ (1-1b)其中,,x y z iv jv kv 称为分矢量。

而i(1,0,0),j(0,1,0),k(0,0,1) (1-1c)是单位矢量，它们组成卡氏系中的一组基矢(称为标架)。

§1-2指标符号上面所述用分量(,,)x y z v v v 或用基矢量i,j,k 来表示矢量的方法，在推广到比三维更高的空间时就有困难了。

因此，发展了另一种记法。

把x 、y 、z 分别记为111,,x y z 这样，一个n 维空间的矢量(无法用直观图表示)用分量表示时为123(,,,...,)n v v v v ν= (1-2a)它可视为一个M 维的单行矩阵，且可写为{}i v ν= (1,2,3,...,)i n =同理，基矢i,j,k 可分别写为123,,e e e ，n 维空间的基矢i e (1,2,3,...,)i n =。

而与式(1-1b)对应的写法为112233n n e v e v e v e v ν=++++ (1-2b)相应的分矢量为11,,,i i e v e v ，其中1e =(0,…,0,1,0,…,0) (1-2c)↑ 顺序第i 个这里i 叫做v 的下标，也有记作jv (如本书第三章以后章节所出现)的，这时j 称为上标。

有些量比矢量更复杂，只用一个下(或上)指标还不够，还要采用更多的指标，比如,,,ij ij ijk A B C ，等等。