第1章--时域离散信号和时域离散系统
- 格式:ppt
- 大小:10.16 MB
- 文档页数:55




时域离散信号:§例:已知模拟信号是一个正弦波,将它转换成时域离散信号和数字信号。
} {,0,0.9sin 50,0.9sin100,0.9sin150T T ππ时域离散信号n 只能取整数总结:时域离散信号可以通过对模拟信号得到,如果将它的每一个序列值经过有限位的,得到一个用二进制编码表示的序列,该序列就数字信号。
序列值一般有无限位小数。
如果用四位二进制数表示的幅度,二进制数第一位表示符号位,该二进制编码形成的信号数字信号数字信号编码、量化号之间是有差别的。
总结:随着二进制编码位数增加,数字信号和时域离散信号之间的差别越来越小。
[x n 换算成十进制,则x(n 位数有关,如果用换算成十进制,则时域离散信号的来源有两类:¾¾例:每天上午压均正常,收缩压不正常,仅记录收缩压并用时域离散信号号也称为时域离散信号表示方法(((x(n)……¾,如果将它的每一个序列值经过有限位的,得到一个用二进制编码表示的序列,该序列就是字信号¾号之间的差别越来越小。
110()00n n n δ=⎧=⎨≠⎩δδ()t δ10 ()00nu nn≥⎧=⎨<⎩101()0n N n N R n ≤≤−⎧=⎨⎩其它4、实指数序列()()nx n a u n =a 为实数5、复指数序列00()()j n j n nx n e e eσωωσ+==⋅00cos()sin()n ne n je n σσωω=+0ω为数字域频率j n n 3x(n)=0.9e π例:6、正弦序列0()sin()x n A n ωφ=+()()sin()a t nTx n x t A nT φ===Ω+0/sT f ω=Ω=Ω0ω:数字域频率Ω:模拟域频率T :采样周期s f :采样频率()sin()a x t A t φ=Ω+模拟正弦信号:数字域频率是模拟域频率对采样频率的归一化频率弧度弧度/秒(x n8x 要使表示成取(3)任何整数例:判断解:如果一个正弦型序列是由一个连续信号采样而得到的,那么,时间间隔得到的采样序列是周期序列呢?设连续正弦信号信号的周期为ω频率乘以频率。



第1章 时域离散信号和时域离散系统 1.1.2 重要公式(1) ∞-∞==-=m n h n x m n h m x n y )(*)()()()( 这是一个线性卷积公式, 注意公式中是在-∞~∞之间对m 求和。
如果公式中x(n)和h(n)分别是系统的输入和单位脉冲响应, y(n)是系统输出, 则该式说明系统的输入、 输出和单位脉冲响应之间服从线性卷积关系。
(2)x(n)=x(n)*δ(n)该式说明任何序列与δ(n)的线性卷积等于原序列。
x(n -n0)=x(n)*δ(n -n0)(3)∞-∞=-=k a n k X T X )j j (1)j (ˆs ΩΩΩ这是关于采样定理的重要公式, 根据该公式要求对信号的采样频率要大于等于该信号的最高频率的两倍以上, 才能得到不失真的采样信号。
∞-∞=--=n a a T nT t T nT t nt x t x /)(π]/)(πsin[)()(这是由时域离散信号理想恢复模拟信号的插值公式。
1.2 解线性卷积的方法解线性卷积是数字信号处理中的重要运算。
解线性卷积有三种方法, 即图解法(列表法)、 解析法和在计算机上用MA TLAB 语言求解。
它们各有特点。
图解法(列表法)适合于简单情况, 短序列的线性卷积, 因此考试中常用, 不容易得到封闭解。
解析法适合于用公式表示序列的线性卷积, 得到的是封闭解, 考试中会出现简单情况的解析法求解。
解析法求解过程中, 关键问题是确定求和限, 求和限可以借助于画图确定。
第三种方法适合于用计算机求解一些复杂的较难的线性卷积, 实验中常用。
解线性卷积也可用Z 变换法,以及离散傅里叶变换求解, 这是后面几章的内容。
下面通过例题说明。
设x(n)=R 4(n), h(n)=R 4(n), 求y(n)=x(n)*h(n)。
该题是两个短序列的线性卷积, 可以用图解法(列表法)或者解析法求解。
表1.2.1给出了图解法(列表法), 用公式可表示为y(n)={…, 0, 0, 1, 2, 3, 4, 3, 2, 1, 0, 0, …}下面用解析法求解, 写出卷积公式为∑∞-∞=∞-∞=-=-=m m m n R m R m n h m x n y )()()()()(44在该例题中, R 4(m)的非零区间为0≤m ≤3, R 4(n -m)的非零区间为0≤n -m ≤3,或写成n -3≤m ≤n ,这样y(n)的非零区间要求m 同时满足下面两个不等式:0≤m ≤3 m -3≤m ≤n上面公式表明m 的取值和n 的取值有关, 需要将n 作分段的假设。



《数字信号处理Ⅰ》作业姓名:学号:学院:2012 年春季学期第一章 时域离散信号和时域离散系统月 日一 、判断:1、数字信号处理和模拟信号处理在方法上是一样的。
( )2、如果信号的取值和自变量都离散,则称其为模拟信号。
( )3、如果信号的取值和自变量都离散,则称其为数字信号。
( )4、时域离散信号就是数字信号。
( )5、正弦序列都是周期的。
( )6、序列)n (h )n (x 和的长度分别为N 和M 时,则)n (h )n (x *的长度为N+M 。
( )7、如果离散系统的单位取样响应绝对可和,则该系统稳定。
( )8、若满足采样定理,则理想采样信号的频谱是原模拟信号频谱以s Ω(采样频率)为周期进行周期延拓的结果。
( )9、序列)n (h )n (x 和的元素个数分别为21n n 和,则)n (h )n (x *有(1n n 21-+)个元素。
( )二、选择1、R N (n)和u(n)的关系为( ):A. R N (n)=u(n)-u(n-N)B. R N (n)=u(n)+u(n-N)C. R N (n)=u(n)-u(n-N-1)D. R N (n)=u(n)-u(n-N+1)2、若f(n)和h(n)的长度为别为N 、M ,则f(n)*h(n)的长度为 ( ): A.N+M B.N+M-1 C.N-M D.N-M+13、若模拟信号的频率范围为[0,1kHz],对其采样,则奈奎斯特速率为( ): A.4kHz B. 3kHz C.2kHz D.1kHz4、LTIS 的零状态响应等于激励信号和单位序列响应的( ): A.相乘 B. 相加 C.相减 D.卷积5、线性系统需满足的条件是( ):A.因果性B.稳定性C.齐次性和叠加性D.时不变性 6、系统y(n)=f(n)+2f(n-1)(初始状态为0)是( ): A. 线性时不变系统 B. 非线性时不变系统 C. 线性时变系统 D. 非线性时变系统7、、若模拟信号的频率范围为[0,Fs],对其采样,则奈奎斯特间隔为( ):A.1/4FsB. 1/3FsC.1/2FsD.1/Fs 三、填空题1、连续信号的( )和( )都取连续变量。
第1章 时域离散信号和时域离散系统上机题答案1.解:求解程序ex115.m如下:%程序ex115.m% 调用filter解差分方程y(n)+0.5y(n-1)=x(n)+2x(n-2)xn=[1,2,3,4,2,1,zeros(1,10)];%x(n)=单位脉冲序列,长度N=31B=[1,0,2];A=[1,0.5];%差分方程系数yn=filter(B,A,xn) %调用filter解差分方程,求系统输出信号y(n) n=0:length(yn)-1;subplot(3,2,1);stem(n,yn,′.′) ;axis([1,15,-2,8])title(′系统的零状态响应′);xlabel(′n′);ylabel(′y(n)′)程序运行结果:yn =[1.0000 1.5000 4.2500 5.8750 5.0625 6.4688 0.76561.6172 -0.8086 0.4043 -0.2021 0.1011 -0.0505 0.0253-0.0126 0.0063 -0.0032 0.0016 -0.0008 0.0004-0.0002 0.0001 -0.0000 0.0000 -0.0000 0.0000]程序运行结果的y(n)波形图如题下图所示。
2.解:(1)系统差分方程的系数向量为B1=1,A1=[1,-0.6,0.08](2)系统差分方程的系数向量为B2=[2,0,-1], A2=[1,-0.7,0.1]调用MATLAB函数filter计算两个系统的系统的单位脉冲响应和单位阶跃响应的程序ex116.m如下:%程序ex116.mB1=1;A1=[1,-0.6,0.08];%设差分方程(1)系数向量B2=[2,0,-1];A2=[1,-0.7,0.1];%设差分方程(2)系数向量%===================================%系统1xn=[1,zeros(1,30)];%xn=单位脉冲序列,长度N=31xi=filtic(B1,A1,ys);%由初始条件计算等效初始条件输入序列xi hn1=filter(B1,A1,xn,xi);%调用filter解差分方程,求系统输出信号hn1n=0:length(hn1)-1;subplot(3,2,1);stem(n,hn1,′.′)title(′(a) 系统1的系统单位脉冲响应′);xlabel(′n′);ylabel(′h(n)′)xn=ones(1,30);%xn=单位阶跃序列,长度N=31sn1=filter(B1,A1,xn,xi);%调用filter解差分方程,求系统输出信号sn1n=0:length(sn1)-1;subplot(3,2,2);stem(n,sn1,′.′)itle(′(b) 系统1的单位阶跃响应′);xlabel(′n′);ylabel(′s(n)′)%======================================%系统2xn=[1,zeros(1,30)];%xn=单位脉冲序列,长度N=31xi=filtic(B2,A2,ys);%由初始条件计算等效初始条件输入序列xihn2=filter(B2,A2,xn,xi);%调用filter解差分方程,求系统输出信号hn2n=0:length(hn2)-1;subplot(3,2,5);stem(n,hn2,′.′)title(′(a) 系统2的系统单位脉冲响应′);xlabel(′n′);ylabel(′h(n)′)xn=ones(1,30);%xn=单位阶跃序列,长度N=31sn2=filter(B2,A2,xn,xi);%调用filter解差分方程,求系统输出信号sn2n=0:length(sn2)-1;subplot(3,2,6);stem(n,sn2,′.′)title(′(b) 系统2的单位阶跃响应′);xlabel(′n′);ylabel(′s(n)′)程序运行结果如下图所示。
·1·第1章 时域离散信号和系统1.1 引 言本章内容是全书的基础。
学生从学习模拟信号分析与处理到学习数字信号处理,要建立许多新的概念,数字信号和数字系统与原来的模拟信号和模拟系统不同,尤其是处理方法上有本质的区别。
模拟系统用许多模拟器件完成,数字系统用运算方法完成。
如果对本章中关于数字信号与系统的若干基本概念不清楚,那么在学习数字滤波器时,会感到不好掌握,因此学好本章是很重要的。
1.2 本章学习要点(1) 关于信号● 模拟信号、时域离散信号、数字信号三者之间的区别。
● 如何由模拟信号产生时域离散信号。
● 常用的时域离散信号。
● 如何判断信号是周期性的,其周期如何计算。
(2) 关于系统● 什么是系统的线性、时不变性,以及因果性、稳定性;如何判断。
● 线性、时不变系统输入和输出之间的关系;求解线性卷积的图解法、列表法、解析法,以及用MA TLAB 工具箱函数求解。
● 线性常系数差分方程的递推解法。
● 用MA TLAB 求解差分方程。
● 什么是滑动平均滤波器,它的单位脉冲响应是什么。
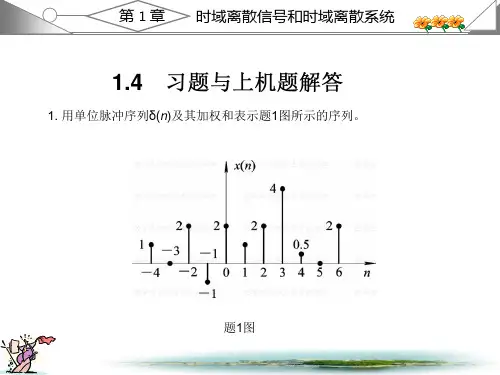
1.3 习题与上机题解答1.1 用单位脉冲序列及其加权和表示图P1.1所示的序列。
解:()(2)(1)2()(1)2(2)3(3)(4)2(6)x n n n n n n n n n δδδδδδδδ=+-+++-+-+-+-+-1.2 给定信号24,4≤≤1()4,0≤≤40,n n x n n +--⎧⎪=⎨⎪⎩其他 (1) 画出x (n )的波形,标上各序列值;(2) 试用延迟的单位脉冲序列及其加权和表示x (n )序列; (3) 令1()2(2)x n x n =-,画出1()x n 的波形; (4) 令2()(2)x n x n =-,画出2()x n 的波形。
·2·解:(1) 画出x (n )的波形,如图S1.2.1所示。
图P1.1 图S1.2.1(2) ()4(4)2(3)2(1)4()4(1)4(2)4(3)4(4)x n n n n n n n n n δδδδδδδδ=+-+++++-+-+-+--。