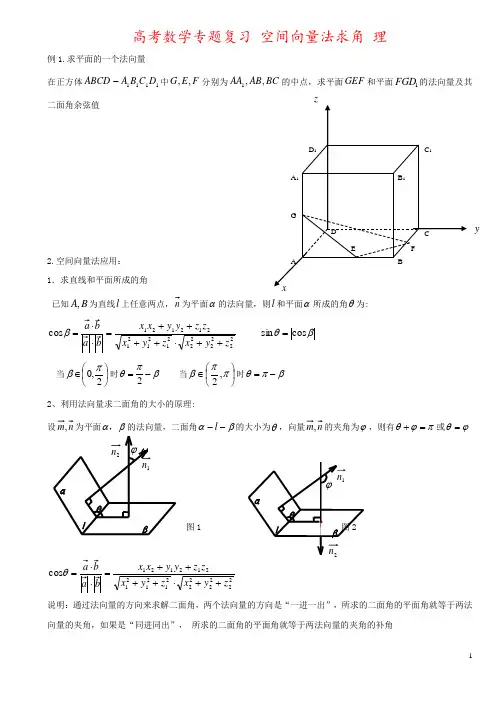
高考数学专题复习 空间向量法求角 理例1.求平面的一个法向量在正方体1111D C B A ABCD -中F E G ,,分别为BC AB AA ,,1的中点，求平面GEF 和平面1FGD 的法向量及其二面角余弦值2.空间向量法应用： 1．求直线和平面所成的角已知B A ,为直线l 上任意两点，n 为平面α的法向量，则l 和平面α所成的角θ为:222222212121212121cos zy x z y x z z y y x x ++⋅++++==β βθcos sin =当⎪⎭⎫ ⎝⎛∈2,0πβ时βπθ-=2 当⎪⎭⎫ ⎝⎛∈ππβ,2时βπθ-= 2、利用法向量求二面角的大小的原理:设n m ,为平面βα，的法向量，二面角βα--l 的大小为θ，向量n m ,的夹角为ϕ，则有πϕθ=+或ϕθ=图222222212121212121cos zy x z y x z z y y x x ++⋅++++==θ说明：通过法向量的方向来求解二面角，两个法向量的方向是“一进一出”，所求的二面角的平面角就等于两法向量的夹角，如果是“同进同出”， 所求的二面角的平面角就等于两法向量的夹角的补角y三. 空间向量法:1.下图分别为三棱锥ABC S -的直观图与三视图，在直观图中，N M SC SA 、,=分别为SB AB ,的中点. （Ⅰ）求证：SB AC ⊥（Ⅱ）求二面角B NC M --的余弦值.2.如图，PDCE 为矩形，ABCD 为梯形，平面PDCE ⊥平面ABCD ，090=∠=∠ADC BAD ，12AB ADCD a ，2PD a .(Ⅰ)若M 为PA 中点，求证：//AC 平面MDE (Ⅱ)求平面PAD 与PBC 所成二面角大小ABCMSN侧视俯视图4A BCEPDMABC1A 1B 1C 3.多面体111ABC A BC -中，11ABB A 是正方形，1AC AB ==，11AC A B BC ==，11//B C BC ，1112B C =BC . （Ⅰ）求证：1//AB 面11AC C（Ⅱ）求二面角11C AC B --的余弦值的大小4.在直四棱柱1111ABCD A BC D -中，底面ABCD 为平行四边形，且2AD =，13AB AA ==，060=∠BAD ，E 为AB 的中点．（Ⅰ）证明：1AC ∥平面1EB C（Ⅱ）求直线1ED 与平面1EB C 所成角的正弦值．5.四棱锥ABCD P -的底面是边长为1的菱形，E BCD ，060=∠是CD 中点，ABCD PA ⊥，3=PA（Ⅰ）证明：平面PAB PBE ⊥ （Ⅱ）求二面角P BE A --的大小.A1ADC1D1C1BBE6.如图，正四棱柱1111ABCD A BC D -中，124AAAB ==，点E 在1CC 上且EC E C 31=． （Ⅰ）证明：1AC ⊥平面BED （Ⅱ）求二面角1A DE B --的余弦值7.四棱锥ABCD P -中，底面ABCD 为平行四边形，ABCD PD AD AB DAB ⊥==∠,2600， (Ⅰ) 证明：BD PA ⊥（Ⅱ）若AD PD =，求二面角C PB A --的余弦值8.已知正三棱柱A B C -111A B C 的底面边长为2，侧棱长为32，点E 在侧棱1A A 上，点F 在侧棱1B B 上，且22A E =,2BF =.（Ⅰ）求证：1C F C E ⊥（Ⅱ）求二面角1E C F C --的大小A BCDEA 1B 1C 1D 19.AD EB AE AEB EF ,,⊥⊥//EF //BC ，G BE AE EF AD BC ，，，2342=====是BC 的中点 （Ⅰ）求证：AB //平面DEG （Ⅱ）求二面角E DF C --的余弦值10.在四棱锥P ABCD -中，底面ABCD 为菱形，060=∠BAD ，Q 为AD 的中点，2PA PD AD === （Ⅰ）点M 在线段PC 上，PM tPC =，试确定t 的值，使//PA 平面MQB（Ⅱ）在（Ⅰ）的条件下，若平面PAD ⊥平面ABCD ，求二面角M BQ C --的大小11.三棱锥被平行于底面ABC 的平面所截得的几何体如图所示，截面为111A B C ，090=∠BAC ，1A A ⊥平面ABC ，13A A =，2AB =，2AC =，111AC =，12BD DC =． （Ⅰ）证明：平面1A AD ⊥平面11BCC B （Ⅱ）求二面角1A CC B --的余弦值A 1AC 1B 1BDC12.直角梯形ABCP 中，AP ∥BC ，1,2,2AP AB AB BC AP D ⊥===是AP 中点,G F E ,,分别为CB PD PC ,,的中点，将PCD ∆沿CD 折起，使得PD ⊥平面ABCD ，如图2（Ⅰ）求证：AP ∥平面EFG （Ⅱ）求二面角D EF G --的大小13.在五面体ABCDE 中，四边形ADEF 是正方形，FA ABCD ⊥平面，//BC AD ，1CD =，22AD =，045=∠=∠CDA BAD（Ⅰ）求异面直线CE 与AF 所成的角的余弦值 （Ⅱ）证明：ABF CD ⊥（Ⅲ）求二面角B EF A --的正切值．14.如图，已知⊥AB 平面DE ACD ,//AB ，ACD ∆是正三角形，AB DE AD 2==，且F 是CD 的中点 （Ⅰ）求证：AF //平面BCE （Ⅱ）求证：CDE BCE ⊥（Ⅲ）求平面BCE 与平面ACD 所成锐二面角的大小BFED CA15.如图，在正三棱柱DEF ABC -中，P AD AB ，，12==是CF 的延长线上一点，过P B A ,,三点的 平面交FD 于M ，交EF 于N （Ⅰ）求证：MN ∥平面CDE（Ⅱ）(文科)当3=PC 时，求三棱台ABC MNF -的体积（Ⅲ）当平面CDE PAB ⊥时，求三棱台ABC MNF -的体积．16.在多面体ABCDEFG 中，平面DG EF DG ED AC BA DEFG AD DEFG ABC //,,,,//⊥⊥⊥且4,2,1======DG AD EF ED AB AC ．（Ⅰ）求证：DEFG BE ⊥ （Ⅱ）求证：ACGD BF //（Ⅲ）求二面角A BC F --的余弦值．17.已知直角梯形ABCD 的上底2BC =1//,2BC AD BC AD =，CD AD ⊥，PDC ⊥ABCD ，PCD ∆是边长为2的等边三角形 （Ⅰ）证明：AB PB ⊥（Ⅱ）求二面角P AB D --的大小 （Ⅲ）求三棱锥A PBD -的体积A BCD EGF18.直三棱柱111ABC A BC -中，5,4,3AB AC BC ===，14AA =，点D 在AB 上． （Ⅰ）若D 是AB 中点，求证：1AC ∥平面1B CD （Ⅱ）当15BD AB =时，求二面角1B CD B --的余弦值． 19. 如图，四边形ABCD 中，AB AD ⊥AD ,∥2,4,6,===AB BC AD BC , 点F E ,分别在AD BC ,上，且E 为BC 中点，EF ∥AB ,现将四边形ABEF 沿EF 折起，使二面角A EF D --等于060 （Ⅰ）设P 为AD 的中点，求证：CP ∥平面ABEF （Ⅱ）求直线AF 与平面ACD 所成角的正弦值．20.如图所示，在矩形ABCD 中，4,2,AB AD E CD ==是的中点，O 为AE 的中点，以AE 为折痕将ADE ∆向上折起，使D 到P 点位置，且PC PB =.（Ⅰ）求证：ABCE PO ⊥（Ⅱ）求二面角B AP E --的余弦值AA 1BCDB 1C 121.在四棱锥ABCD P -中，底面是边长为32的菱形，且0120=∠BAD ，且ABCD PA ⊥,N M PA 、,62=分别为PD PB ,的中点．（Ⅰ）证明：MN ∥平面ABCD（Ⅱ）过点A 作PC AQ ⊥，垂足为点Q ，求二面角Q MN A --的余弦值．22.在四棱锥ABCD P -中，DAB ABCD PA ∠⊥,为直角，F E AB CD AD CD AB 、,2,//==分别为CD PC ,的中点.（Ⅰ）求证：BEF CD ⊥（Ⅱ）设()0,>=k kAB PA ，且二面角C BD E --的大小为030，求此时k 的值.23.如图，四边形ABCD 为矩形，PD ABCD PD ,⊥//PD AD QA QA 21,== （Ⅰ）求证：平面DCQ PQC ⊥（Ⅱ）若二面角C BP Q --的余弦值为53-，求AB AD的值24.几何体111ABCD BC D -中，四边形ABCD 为菱形，060=∠BAD ，AB a =，面111B C D ∥面ABCD , 1BB 、1CC 、1DD 都垂直于面ABCD ,且12BB a =，E 为1CC 的中点，F 为AB 的中点.（Ⅰ）求证：1DB E ∆为等腰直角三角形 （Ⅱ）求二面角1B DE F --的大小25.四棱锥A BCDE -中，底面BCDE 为矩形，侧面ABC ⊥底面BCDE ，2BC =，2CD =AB AC =．（Ⅰ）证明：AD CE ⊥（Ⅱ）设侧面ABC 为等边三角形，求二面角C AD E --的余弦值26.在三棱锥P ABC -中，PA ⊥0090,60,,=∠=∠=BCA ABC AB PA ABC ，点D ，E 分别在棱,PB PC 上，且//DE BC（Ⅰ）求证：BC ⊥平面PAC（Ⅱ）当D 为PB 的中点时，求AD 与平面PAC 所成的角的正弦值 （Ⅲ）是否存在点E 使得二面角A DE P --为直二面角BCDF1B 1C 1D CDEAB27.四棱锥S ABCD -中，底面ABCD 为矩形，SD ⊥ABCD ，2AD =2DC SD ==，点M 在侧棱SC 上，ABM ∠060=（Ⅰ）证明：M 在侧棱SC 的中点 （Ⅱ）求二面角S AM B --的余弦值28.在五面体ABCDEF 中，FA ⊥平面ABCD , AD //BC //FE ，AD AB ⊥，M 为EC 的中点，AD FE BC AB AF 21==== （Ⅰ）求异面直线BF 与DE 所成的角的大小 （Ⅱ）证明平面AMD ⊥平面CDE （Ⅲ）求二面角F CD A --的余弦值29. 三棱柱111ABC A BC -，90=∠BCA ，2AC BC ==，1A 在底面射影为AC 中点D ，11BA AC ⊥. （Ⅰ）求证：1AC ⊥平面1A BC （Ⅱ）求二面角1A A B C --的余弦值D1B 1A 1CBAA BCDEF30.矩形ABCD 和梯形BEFC 所在平面互相垂直，BE //2,390,0===∠=∠EF AD CEF BCF CF ，，（Ⅰ）求证：AE //平面DCF（Ⅱ）当AB 的长为何值时, 二面角C EF A --的大小为06031.如图，在直三棱柱111ABC A BC -中，平面1A BC ⊥侧面11.A ABB （Ⅰ）求证：BC AB ⊥（Ⅱ）若1AA AC a ==，直线AC 与平面1A BC 所成的角为θ，二面角A BC A --1的大小为ϕ，求证： 2πϕθ=+32.已知四棱锥P ABCD -的底面是正方形，PA ⊥面ABCD ，且2PA AD ==,点,M N 分别在,PD PC 上，1,.2PN NC PM MD == （Ⅰ） 求证：PC ⊥面AMN（Ⅱ）求二面角B AN M --的余弦值.DMNP A33.已知正三棱柱111C B A ABC -的底面边长是2，D 是侧棱1CC 的中点，平面ABD 和平面C B A 11的交线为MN（Ⅰ）试证明MN AB //（Ⅱ）若直线AD 与侧面C C BB 11所成的角为045，试求二面角C BD A --的正切值34.三棱柱111ABC A BC -中,15,4AB AC AA BC ====,1A 在底面ABC 的投影是线段BC 的中点O （Ⅰ）证明在侧棱1AA 上存在一点E ,使得OE ⊥平面11BB C C ,并求出AE 的长 (Ⅱ)求平面11A B C 与平面11BB C C 夹角的余弦值35.如图,在长方体1111ABCD A BC D -中E AD AA ,11==为CD 中点. (Ⅰ)求证:11B E AD ⊥(Ⅱ)在棱1AA 上是否存在一点P ,使得//DP 平面1B AE ?若存在,求AP 的长;若不存在,说明理由(Ⅲ)若二面角11A B E A --的大小为030,求AB 的长.36.正△ABC 的边长为4，CD 是AB 边上的高，,E F 分别是AC 和BC 边的中点，现将△ABC 沿CD 翻折成直二面角A DC B --．(Ⅰ)试判断直线AB 与平面DEF 的位置关系，并说明理由 （Ⅱ）求二面角E DF C --的余弦值(Ⅲ)在线段BC 上是否存在一点P ，使AP DE ⊥？证明你的结论．37.四棱锥A BCDE -中，BCDE 为矩形，侧面ABC ⊥底面BCDE ，2BC =，CD =AB AC =．（Ⅰ）证明：AD CE ⊥（Ⅱ）设CE 与平面ABE 所成的角为045，求二面角C AD E --的余弦值例1：()()29873cos ,4,3,2,1,1,1-==---=θn m ()()()()()()11333,2,6.0,32,2:,1,6,2.0,3,3,3,3,2:1⇒-==--===n CB BNC m CM CN MNC ()()()()()().31cos 1,1,1:,1,1,1:3.32,1,1,0,1,021111=⇒--=-=⇒==θπn B C A m C C A n m ()()()70309cos sin ,3,32,5,0,21,3,0,0,04==--=⎪⎭⎫⎝⎛θαm E D CDEABABCDEFAB CDEF()()().31,3,0:,1,0,0:.5πθ=⇒==⊥n PBC m ABE PAB BE ()()()4214,2,1,1,2,1,46---()()()()()772cos 3,0,2:,32,3,1:.0,1,3,0007-=--==-θn PBA m PBC A D ，， ()()40,3,1:,1,2,0:πθ=⇒==n CFC m ECF()()()66cos 0,0,1:,1,2,1:.332,31,233,21,239-=⇒=-=⎪⎪⎭⎫ ⎝⎛⇒⎪⎪⎭⎫⎝⎛-θn DFE m CDF M P ()()2,3,3:,3131,//10-==⇒=m MBQ t AC AE BE PA ()31,0,0:π⇒=n BCQ ()()()5150,0,1,1,3,611⇒==n m ().412π()4113()()()41,0,0,1,0,114π⇒=-=n m ()27319,315==V CP ()()()661,2,1,1,0,0,//16-⇒=-=n m DE AB ()()3,1,2:,17222==+m ABP AP BP AB()362,41,0,0:=⇒=V n ABD π()()()1333,12,4:,1,0,0:181⇒--CDB BCD ().5219()3320().333321 ()()()().1522,2,:,1,0,0:,,0,0,////22⇒-k k n m k P EBF PAD CD ()()()12,,0:,1,,:23=⇒--AB k n k k m ()()()42,1,0:,2,1,3:24π⇒--n m ()10125-().73,,4226CP CE PC AE DE AE =⇒⊥⊥ ()()()()()36cos 2,0,1:,1,1,2:,210,2,0,2,2,227-=⇒--=⇒-=--=+=θn m t BA t t CM BC BM()36,328π()()()()771,3,0,1,3,3,3,0,0,,291111⇒-=-==⇒⊥⊥n m t t A BC AC BA AC ()()()()()()()()2933,,3,1,0,0.0,3,1,,0,3.0,3,4,0,0,3,,0,030=⇒-===-=k k k n m EF k AE F E k A []()()()22111sin sin ,2131ca c c AB ACM ABMB A AM B CN BB B A CN +==⇒==∠=∠⇒⊥⊥⇒⊥ϕθθϕ，作()()()5151,1,1:,1,2,0:.34,32,32,32,32,3232-⇒--⎪⎭⎫⎝⎛⎪⎭⎫ ⎝⎛-=n m N PC ()()()()3tan 101cos 1,0,0,1,6,3,3,0,1,233=⇒=⇒=-==θθn m A CD ()()1030cos 2.51,52,431===⇒⊥⊥θAE OE BC OE AA OE[]()()()()()()21,1,0:,2,,2:.1,1,2,1,1,2,0,0,3.21,0,02.1351111111=⇒=-=⎪⎭⎫⎝⎛-=⎪⎭⎫ ⎝⎛--=⎪⎭⎫ ⎝⎛⊥t n E B A t t m E AB t EA t E B t B p CE B BC ()BC BP 31,72136=()()()()()101cos 2,3,0:,1,0,3:.31,0,:,0,037-=⇒=-=⇒=⇒-=⇒θn ADE m CAD k k m ABE k A 2004-2014山东高考数学真题：立体几何（04）如图，已知四棱锥ABCD P -，AD PB ⊥，侧面PAD 为边长等于2的正三角形，底面ABCD 为菱形，侧面PAD 与底面ABCD 所成的二面角为0120.求点P 到平面ABCD 的距离（05）已知长方体1111ABCD A BC D -,12,1AB AA ==，直线BD 与平面11AA B B 所成的角为030， AE 垂直BD 于,E F 为11A B 的中点．（Ⅰ）求异面直线AE 与BF 所成的角的余弦值（Ⅱ）求平面BDF 与平面1AA B 所成二面角（锐角）的余弦值 （Ⅲ）求点A 到平面BDF 的距离A 11C 11F E CA（06理科）如图，已知平面111C B A 平行于三棱锥ABC F -的底面ABC ，等边C AB 1∆所在的平面与 底面ABC 垂直，且090=∠ACB ，设a BC a AC ==,2 （Ⅰ）求证直线11C B 是异面直线1AB 与11C A 的公垂线 （Ⅱ）求点A 到平面FBC 的距离 （Ⅲ）求二面角C FB A --的余弦值（07理科）在直四棱柱1111ABCD A BC D -中,已知122DC DD AD AB ===,AD DC ⊥.AB //CD （Ⅰ）设E 是DC 的中点, 求证: E D 1//BD A 1 （Ⅱ）求二面角11A BD C --的余弦值ED1C1B1A1DCBA（08理科）四棱锥P ABCD -底面为菱形，PA ⊥平面ABCD ，060=∠ABC ，E F ，是BC PC ，中点 （Ⅰ）证明：AE PD ⊥（Ⅱ）若H 为PD 上的动点，EH 与PADE AF C --的余弦值．（08文科）在四棱锥P ABCD -中，平面PAD ⊥平面ABCD ，AB //DC ，PAD △是等边三角形，已知28BD AD ==，2AB DC ==（Ⅰ）设M 是PC 上的一点，证明：平面MBD ⊥平面PAD （Ⅱ）求四棱锥P ABCD -的体积．ABCMPDPBEC DFA（09文理）直四棱柱1111D C B A ABCD -中，ABCD 为等腰梯形，AB //CD ,，，24===CD BC AB21=AA ，M E ,分别是棱1,AA AD 的中点.设F 是棱AB 的中点（Ⅰ）证明：直线EM //平面1FCC （Ⅱ）证明:平面C C BB AC D 111⊥（文科） （Ⅲ）求二面角C FC B --1的余弦值（10理科）在五棱锥ABCDE P -中，⊥PA 平面AB ABCDE ,//AC CD ,//AE ED ,//BC ，,450=∠ABC 42,22===AE BC AB ，三角形PAB 是等腰三角形（Ⅰ）求证：平面PCD ⊥平面PAC （Ⅱ）求直线PB 与平面PCD 所成角的大小 （Ⅲ）求四棱锥ACDE P -的体积EA BCFMAB 1C 1DD（10文科）在如图所示的几何体中，四边形ABCD 是正方形，⊥MA G F E MA PD ABCD ,,,//,分别为PC PB MB ,,的中点，且MA PD AD 2==（Ⅰ）求证：平面PDC EFG ⊥（Ⅱ）求三棱锥MAB P -与四棱锥ABCD P -的体积之比（11文科）四棱台中，1D D ⊥ABCD ，ABCD 是平行四边形，01160,,2=∠==BAD B A AD AD AB （Ⅰ）证明:BD AA ⊥1 （Ⅱ）证明:BD A CC 11（11理科）如图所示的几何体中，四边形ABCD 为平行四边形，090,ACB ∠=ABCD EA ⊥ //,//,//,2EF AB FG BC EG AC AB EF = （Ⅰ）若M 是线段AD 的中点，求证：ABFE GM // （Ⅱ）若2AC BC AE ==，求二面角A BF C --的大小.DB 11DC 1 CBA A 1 DEFG（12理科）如图几何体中，四边形ABCD 是等腰梯形，AB //CD ，060=∠DAB ，ABCD FC ⊥， CF CD CB BD AE ==⊥,（Ⅰ）求证：AED BD ⊥（Ⅱ）求二面角C BD F --的余弦值（12文科）几何体E ABCD -是四棱锥，ABD ∆为正三角形，,CB CD EC BD =⊥.（Ⅰ）求证：DE BE =（Ⅱ）若0120=∠BCD ，M 为线段AE 的中点，求证：DM //平面BEC .（13理科）在三棱锥ABQ P -中，F E C D BQ BP BA ABQ PB ,,,.,==⊥，分别是BP AP BQ AQ ,,, 的中点，PD BD AQ ,2=与EQ 交于点PC G ,与FQ 交于点H ，连接GH（Ⅰ）求证：AB //GH（Ⅱ）求二面角E GH D --的余弦值（13文科）四棱锥P ABCD -中，,AB AC AB PA ⊥⊥,,2AB CD AB CD =∥,,,,,E F G M N 分别为,,,,PB AB BC PD PC 的中点（Ⅰ）求证：PAD CE //（Ⅱ）求证：EMN EFG ⊥(14理)四棱柱1111D C B A ABCD -，底面ABCD 是等腰梯形，M CD AB DAB ,22,600===∠是线段AB 中点 （Ⅰ）求证：111//ADD A M C（Ⅱ）若ABCD CD ⊥1且31=CD ，求平面M D C 11和ABCD 所成角（锐角）的余弦值B 1C 1D 1A 1DC B M A（14文）四棱锥ABCD P -中F E AD BC AB BC AD PCD AP ,,21,//,==⊥分别为线段PC AD ,的中点 （Ⅰ）求证：BEF AP //（Ⅱ）求证：PAC BE ⊥（04）23（05）()().5525151,3,1,0,1,042，，⇒==n m （06）(),1,3,32,333--=⇒=m a V ().411,3,0⇒=n （07）()()331,1,1,1,2,2⇒-=--=n m （08理）()()5150,3,1,1,2,0⇒-=-=n m（08文科）316（09理）()().773,0,2,0,3,1⇒==n m （10理）()()⇒=-=1,1,0,22,0,22m BP .6πθ=22（11理）3π（12理）55(13理)54-（14）55。
