电磁感应现象中的力学问题(1)

高考物理电磁感应知识点归纳高考物理电磁感应知识点归纳1.电磁感应现象电磁现象：利用磁场产生电流的现象称为电磁感应，产生的电流称为感应电流。

(1)产生感应电流的条件：通过闭合电路的磁通量发生变化，即0。

(2)产生感应电动势的条件：无论回路是否闭合，只要通过线圈平面的磁通量发生变化，线路中就会产生感应电动势。

导体中产生感应电动势的部分相当于电源。

(3)电磁感应的本质是产生感应电动势。

如果回路闭合，会有感应电流；如果回路不闭合，只会有感应电动势而没有感应电流。

2.磁通量(1)定义：磁感应强度b与垂直于磁场方向的面积s的乘积称为通过这个表面的磁通量，定义公式为=BS。

如果面积S不垂直于B，则B应乘以垂直于磁场方向的投影面积S，即=BS，SI单位：Wb。

在计算磁通量时，应该是通过某一区域的磁感应线的净数量。

每张脸都有正面和背面；当磁感应线从表面的正方向穿透时，通过表面的磁通量为正。

相反，磁通量是负的。

磁通量是穿过正面和背面的磁感应线的代数和。

3.楞次定律(1)楞次定律：感应电流的磁场总是阻碍引起感应电流的磁通量的变化。

楞次定律适用于感应电流方向的一般判断，而右手定则只适用于剪线时磁感应线的运动，用右手定则比楞次定律更容易判断。

(2)理解楞次定律(1)谁阻碍谁——感应电流的磁通量阻碍了感应电流的磁通量。

阻碍——阻碍的是通过回路的磁通量的变化，而不是磁通量本身。

如何阻碍——当一次磁通增加时，感应电流的磁场方向与一次磁场方向相反；当一次磁通量减少时，感应电流的磁场方向与一次磁场的方向相同，即，一次磁通量增加，一次磁通量减少。

阻塞-阻塞的结果不是停止，而是增加和减少。

(3)楞次定律的另一种表述：感应电流总是阻碍其产生的原因，表现形式有三种：(1)阻碍原始磁通量的变化；阻碍物体之间的相对运动；阻止一次电流(自感)的变化。

4.法拉第电磁感应定律电路中感应电动势的大小与通过电路的磁通量的变化率成正比。

表达式E=n/t当导体切割磁感应线时，感应电动势公式为E=BLvsin。

电磁感应中的力学问题电磁感应中中学物理的一个重要“节点”，不少问题涉及到力和运动、动量和能量、电路和安培力等多方面的知识，综合性强，也是高考的重点和难点，往往是以“压轴题”形式出现．因此，在二轮复习中，要综合运用前面各章知识处理问题，提高分析问题、解决问题的能力． 本学案以高考题入手，通过对例题分析探究，让学生感知高考命题的意图，剖析学生分析问题的思路，培养能力．例1.【2003年高考江苏卷】如右图所示，两根平行金属导端点P 、Q 用电阻可忽略的导线相连，两导轨间的距离l =0.20 m ．有随时间变化的匀强磁场垂直于桌面，已知磁感应强度B 与时间t 的关系为B=kt ，比例系数k ＝0.020 T ／s ．一电阻不计的金属杆可在导轨上无摩擦地滑动，在滑动过程中保持与导轨垂直．在t=0时刻，轨固定在水平桌面上，每根导轨每m 的电阻为r 0＝0.10Ω／m ，导轨的金属杆紧靠在P 、Q 端，在外力作用下，杆恒定的加速度从静止开始向导轨的另一端滑动，求在t ＝6.0 s 时金属杆所受的安培力． [解题思路] 以a 示金属杆运动的加速度，在t 时刻，金属杆与初始位置的距离L ＝21at 2 此时杆的速度v ＝at这时，杆与导轨构成的回路的面积S=L l回路中的感应电动势E ＝StB∆∆＋B lv 而ktBtt t B t B ktB =∆-∆+=∆∆=)( 回路的总电阻 R ＝2Lr 0 回路中的感应电流，REI=作用于杆的安培力F ＝BlI解得t r l k F 02223= 代入数据为F ＝1.44×10-3N例2． (2000年高考试题)如右上图所示，一对平行光滑R 轨道放置在水平地面上，两轨道间距L ＝0.20 m ，电阻R ＝1.0 Ω；有一导体杆静止地放在轨道上，与两轨道垂直，杆与轨道的电阻皆可忽略不计，整个装置处于磁感强度B ＝0.50T 的匀强磁场中，磁场方向垂直轨道面向下．现用一外力F 沿轨道方向拉杆，使之做匀加速运动．测得力F 与时间t 的关系如下图所示．求杆的质量m 和加速度a ．解析：导体杆在轨道上做匀加速直线运动，用v 表示其速度，t 表示时间，则有v ＝at ① 杆切割磁感线，将产生感应电动势E ＝BLv ②在杆、轨道和电阻的闭合回路中产生电流I=E/R ③ 杆受到的安培力为F 安=IBL ④ 根据牛顿第二定律，有F －F 安＝ma ⑤联立以上各式，得at Rl B ma F 22= ⑥由图线上各点代入⑥式，可解得 a ＝10m/s 2，m ＝0.1kg例3． (2003年高考新课程理综)两根平行的金属导轨，固定在同一水平面上，磁感强度B ＝0.05T 的匀强磁场与导轨所在平面垂直，导轨的电阻很小，可忽略不计．导轨间的距离l ＝0.20 m ．两根质量均为m ＝0.10 kg 的平行金属杆甲、乙可在导轨上无摩擦地滑动，滑动过程中与导轨保持垂直，每根金属杆的电阻为R ＝0.50Ω．在t ＝0时刻，两杆都处于静止状态．现有一与导轨平行、大小为0.20 N 的恒力F 作用于金属杆甲上，使金属杆在导轨上滑动．经过t ＝5.0s ，金属杆甲的加速度为a ＝1.37 m ／s ，问此时两金属杆的速度各为多少?本题综合了法拉第电磁感应定律、安培力、左手定则、牛顿第二定律、动量定理、全电路欧姆定律等知识，考查考生多角度、全方位综合分析问题的能力．设任一时刻t ，两金属杆甲、乙之间的距离为x ，速度分别为v l 和v 2，经过很短的时间△t ，杆甲移动距离v 1△t ，杆乙移动距离v 2△t ，回路面积改变△S ＝[(x 一ν2△t )+ν1△t]l —l χ＝(ν1-ν2) △t 由法拉第电磁感应定律，回路中的感应电动势 E ＝B △S/△t ＝B ι(νl 一ν2) 回路中的电流 i ＝E ／2 R杆甲的运动方程 F —B l i ＝ma由于作用于杆甲和杆乙的安培力总是大小相等、方向相反，所以两杆的动量(t ＝0时为0)等于外力F 的冲量．Ft ＝m νl ＋m ν2 联立以上各式解得ν1＝[Ft/m ＋2R(F 一ma)／B 2l 2]／2 ν2＝[Ft ／m 一2R(F 一ma)／B 2l 2]／2代入数据得移νl ＝8.15 m ／s ，v 2＝1.85 m ／s 练习1、．如图l ，ab 和cd 是位于水平面内的平行金属轨道，其电阻可忽略不计．af 之间连接一阻值为R 的电阻．ef 为一垂直于ab 和cd 的金属杆，它与ab 和cd 接触良好并可沿轨道方向无摩擦地滑动．ef 长为l ，电阻可忽略．整个装置处在匀强磁场中，磁场方向垂直于图中纸面向里，磁感应强度为B ，当施外力使杆ef 以速度v 向右匀速运动时，杆ef 所受的安培力为( )．R lvB A 2.R vBlB R lvB C 2 RvBl D 2图1图22、如图2所示·两条水平虚线之间有垂直于纸面向里、宽度为d 、磁感应强度为B 的匀强磁场．质量为m 、电阻为R 的正方形线圈边长为L(L<d)，线圈下边缘到磁场上边界的距离为h ．将线圈由静止释放，其下边缘刚进入磁场和刚穿出磁场时刻的速度都是v 0在整个线圈穿过磁场的全过程中(从下边缘进入磁场到上边缘穿出磁场)，下列说法中正确的是( )． A·线圈可能一直做匀速运动 B ．线圈可能先加速后减速C ．线圈的最小速度一定是mgR ／B 2 L 2D ．线圈的最小速度一定是)(2l d h g +-3、如图3所示，竖直放置的螺线管与导线abed 构成回路，导线所围区域内有一垂直纸面向里的变化的匀强磁场，螺线管下方水平面桌面上有一导体圆环．导线abcd 所围区域内磁场的磁感强度按图1 5—11中哪一图线所表示的方式随时问变化时，导体圆环将受到向上的磁场力作用?( )．图3A B CD4、如图4所示，磁感应强度的方向垂直于轨道平面倾斜向下，当磁场从零均匀增大时，金属杆ab 始终处于静止状态，则金属杆受到的静摩擦力将( )．A ．逐渐增大B ．逐渐减小C ．先逐渐增大，后逐渐减小D ．先逐渐减小，后逐渐增大图45、如图所示，一闭合线圈从高处自由落下，穿过一个有界的水平方向的匀强磁场区(磁场方向与线圈平面垂直)，线圈的一个边始终与磁场区的边界平行，且保持竖直的状态不变．在下落过程中，当线圈先后经过位置I 、Ⅱ、Ⅲ时，其加速度的大小分别为a 1、a 2、a 3( )．A ． a 1<g ，a 2=g ，a 3<gB ．a l <g ，a 2<g ，a 3<gC ． a 1<g,a 2=0,a 3=gD ．a 1<g ，a 2>g ，a 3<g图5 图66、如图6所示，有两根和水平方向成a 角的光滑平行的金属轨道，上端接有可变电阻R ，下端足够长，空间有垂直于轨道平面的匀强磁场，磁感强度为B ．一根质量为m 的金属杆从轨道上由静止滑下，经过足够长的时间后，金属杆的速度会趋近于一个最大速度Vm ,则( )．A ．如果B 增大，Vm 将变大 B ．如果a 变大， Vm 将变大C ．如果R 变大，Vm 将变大D ．如果M 变小，Vm 将变大7、超导磁悬浮列车是利用超导体的抗磁作用使列车车体向上浮起，同时通过周期性地变换磁极方向而获得推进动力的新型交通工具．其推进原理可以简化为如图6所示的模型：在水平面上相距L 的两根平行直导轨问，有竖直方向等距离分布的匀强磁场B 1和B 2，且B 1=B 2=B ，每个磁场的宽都是ι，相间排列，所有这些磁场都以速度V 向右匀速运动．这时跨在两导轨间的长为L 、宽为ι的金属框abcd(悬浮在导轨上方)在磁场力作用下也将会向右运动．设金属框的总电阻为R ，运动中所受到的阻力恒为f ，则金属框的最大速度可表示为( )．图7A 、2222/)(L B fR v L B v m -= B 、22222/)2(L B fR v L B v m -= C 、22224/)4(L B fR v L B v m -= D 、22222/)2(L B fR v L B v m+= 答案： 1 .A 2. D 3. A 4. D 5.B 6.BC 7. C8、水平面上两根足够长的金属导轨平行固定放置，间距为L ，一端通过导线与阻值为R 的电阻连接；导轨上放一质量为m 的金属杆(见图)，金属杆与导轨的电阻不计；均匀磁场竖直向下．用与导轨平行的恒定力F 作用在金属杆上，杆最终将做匀速运动．当改拉力的大小时，相对应的匀速运动速度v 也会改变，v 和F 的关系如图 (取重力加速度g=10m ／s 2) (1)金属杆在匀速运动之前做作什么运动?(2)若m ＝0.5 kg ，L ＝0.5 m ，R ＝0.5 Ω，磁感应强度B 为多大? (3)由ν－F 图线的截距可求得什么物理量?其值为多少?解： (1)变速运动(或变加速运动、加速度减小的加速运动，加速运动)． (2)感应电动势E —vBL ，感应电流I=E/R安培力RLvB BIL F m22== 由图可知金属杆受拉力、安培力和阻力作用，匀速时合力为零f RLvB BIL F +==22)(22f F l B Rv -=由图线可以得到直线的斜率k=2)(12T kLR B ==(3)由直线的截距可以求得金属杆受到的阻力f ， f=2(N)．若金属杆受到的阻力仅为动摩擦力，由截距可求得动摩擦因数 μ=0.49、如图所示，两根足够长的直金属导轨MN 、PQ 平行放置在倾角为θ的绝缘斜面上，两导轨间距为L ，M 、P 两点间接有阻值为R 的电阻．一根质量为m 的均匀直金属杆ab 放在两导轨上，并与导轨垂直整套装置处于磁感应强度为B 的匀强磁场中，磁场方向垂直斜面向下，导轨和金属杆的电阻可忽略·让ab 杆沿导轨由静止开始下滑，导轨和金属杆接触良好，不计它们之间的摩擦． (1)由b 向a 方向看到的装置如图1 5—2所示，请在此图中画出ab 杆下滑过程中某时刻的受力示意图； (2)在加速下滑过程中，当杆ab 的速度大小为v 时，求此时ab 杆中的电流及其加速度的大小； (3)求在下滑过程中，ab 杆可以达到的速度最大值．解：(1)重力mg ，竖直向下；支撑力N ，，垂直斜面向上；安培力F ，沿斜面向上．(2)当ab 杆速度为v 时，感应电动势E=BLv ，此时电路电流RBlvR E I ==杆受到安培力Rv L B Blv F 22==根据牛顿运动定律，有：R v L B mg ma 22sin -=θ R vL B g a 22sin -=θ(3)当RvL B mg 22sin =θ时，ab 杆达到最大速度mAX V22sin LB mgR V m θ=10．如图所示，电阻不计的平行金属导轨MN 和OP 水平放置，MO 间接有阻值为R 的电阻，导轨相距为d ，其间有竖直向下的匀强磁场，磁感强度为B ．质量为m 、电阻为r 的导体棒CD 垂直于导轨放置，并接触良好．用平行于MN 的恒力F 向右拉动CD ，CD 受恒定的摩擦阻力．f ，已知F>f ．问： (1)CD 运动的最大速度是多少?(2)当CD 达到最大速度后，电阻R 消耗的电功率是多少? (3)当CD 的速度是最大速度的1/3时，CD 的加速度是多少?解析：(1)以金属棒为研究对象，当CD 受力：F=F A +f 时，CD 速度最大，即：2222))((dB r R f F v f r R v d B f BId F m +-=⇒++=+= (2)CD 棒产生的感应电动势为：Bdr R f F Bdv E m))((--==回路中产生的感应电流为：BdfF r R E I -=+=则R 中消耗的电功率为：2222)(dB Rf F R I R P -== (3)当CD 速度为最大速度的1/3即m v v 31=时，CD 中的电流为最大值的1/3即I I 31'=则CD 棒所受的安培力为：)(31''f F d BI F A-== CD 棒的加速度为：mf F m F f F a A 3)(2'-=--=。

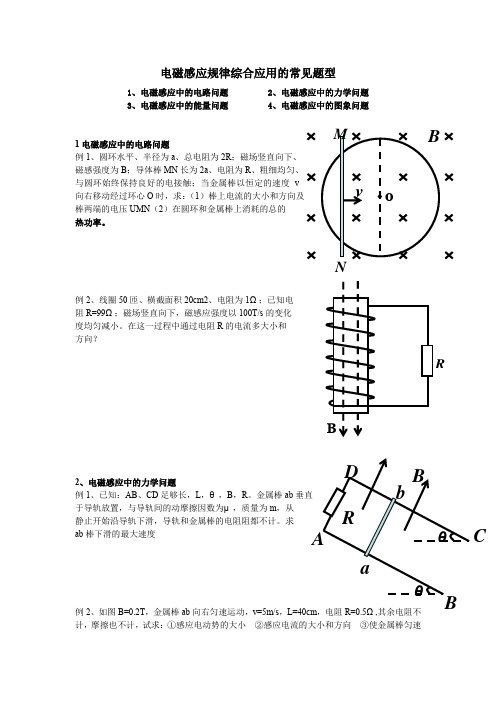
RC电磁感应规律综合应用的常见题型1、电磁感应中的电路问题2、电磁感应中的力学问题3、电磁感应中的能量问题4、电磁感应中的图象问题1电磁感应中的电路问题例1、圆环水平、半径为a 、总电阻为2R ；磁场竖直向下、 磁感强度为B ；导体棒MN 长为2a 、电阻为R 、粗细均匀、与圆环始终保持良好的电接触；当金属棒以恒定的速度v 向右移动经过环心O 时，求：（1）棒上电流的大小和方向及 棒两端的电压UMN （2）在圆环和金属棒上消耗的总的 热功率。

例2、线圈50匝、横截面积20cm2、电阻为1Ω；已知电 阻R=99Ω；磁场竖直向下，磁感应强度以100T/s 的变化 度均匀减小。

在这一过程中通过电阻R 的电流多大小和 方向？2、电磁感应中的力学问题例1、已知：AB 、CD 足够长，L ，θ，B ，R 。

金属棒ab 垂直 于导轨放置，与导轨间的动摩擦因数为μ，质量为m ，从 静止开始沿导轨下滑，导轨和金属棒的电阻阻都不计。

求 ab 棒下滑的最大速度例2、如图B=0.2T ，金属棒ab 向右匀速运动，v=5m/s ，L=40cm ，电阻R=0.5Ω,其余电阻不计，摩擦也不计，试求：①感应电动势的大小 ②感应电流的大小和方向 ③使金属棒匀速0 4 8 1216 20 24 28B 运动所需的拉力 ④感应电流的功率 ⑤拉力的功率例3、导轨光滑、水平、电阻不计、间距L=0.20m ；导体棒长也为L 、电阻不计、垂直静止于导轨上；磁场竖直向下且B=0.5T ；已知电阻R=1.0Ω；现有一个外力F 沿轨道拉杆 ，使之做匀加速运动，测得F 与时间t 的关系如图所示，求杆的质量和加速度a 。

3、电磁感应中的能量问题 例1、θ=30º，L=1m ，B=1T ，导轨光滑电阻不计，F 功率恒定且为6W ，m=0.2kg 、R=1Ω，B tt t tA B C Dab由静止开始运动，当s=2.8m时，获得稳定速度，在此过程中ab产生的热量Q=5.8J，g=10m/s2，求：（1）ab棒的稳定速度（2）ab棒从静止开始达到稳定速度所需时间。

电磁感应中的力学问题1．如图5-2-6甲，闭合线圈从高处自由下落一段时间后垂直于磁场方向进入一有界磁场，在边刚进入磁场到边刚进入磁场的这段时间内，线圈运动的速度图象可能是图5-2-6乙中的哪些图 (ACD )2，如图所示，处于匀强磁场中的两根足够长、电阻不计的平行金导轨相距1m ，导轨平面与水平面成θ＝37o 角，下端连接阻值为R 的电阻，匀强磁场方向与导轨平面垂直，质量为0.2kg ，电阻不计的金属棒放在两导轨上，棒与导轨垂直并保持良好接触，它们之间的动摩擦因数为0.25．（1）求金属棒沿导轨由静止开始下滑时的加速度大小；（2）当金属棒下滑速度达到稳定时，电阻R 消耗的功率为8W ，求该速度的大小；（3）在上问中，若R ＝2Ω，金属棒中的电流方向由a 到b ，求磁感应强度的大小与方向．（g ＝10m/s 2，sin37o＝0.6，cos37o ＝0.8）解答：（1）金属棒开始下滑的初速度为零，根据牛顿第二定律mg sin θ－μmg cos θ＝ma ①由①式解得： a ＝4m/s 2 ②（2）设金属棒运动达到稳定时，速度为v ，所受安培力为F ，棒在沿导轨方向受力平衡mg sin θ－μmg cos θ－F ＝0 ③此时金属棒克服安培力做功的功率等于电路中电阻R 消耗的电功率Fv ＝P ④由③④两式解得 10P v F==m/s ⑤ （3）设电路中电流为I ，两导轨间金属棒长为l ，磁场的磁感应强度为BBlv I R= ⑥ P ＝I 2R ⑦由⑥⑦两式解得0.4B vl==T ⑧ 磁场方向垂直导轨平面向上． 3．如图11， 电动机用轻绳牵引一根原来静止的长l =1m ，质量m =0.1kg 的导体棒AB ，导体棒的电阻R =1Ω，导体棒与竖直“∏”型金属框架有良好的接触，框架处在图示方向的磁感应强度为B =1T 的匀强磁场中，且足够长，已知在电动机牵引导体棒时，电路中的电流表和电压表的读数分别稳定在I=1A 和U =10V ，电动机自身内阻r =1Ω，不计框架电阻及一切摩擦，取g =10m/s 2，求：导体棒到达的稳定速度？4.5m/sB b cA B C D 图5-2-6 甲 乙4．如图5-2-7，在光滑的水平面上有一半径为r ＝10cm ，电阻Ｒ＝1Ω，质量m ＝1kg 的金属圆环，以速度v ＝10m/s 向一有界磁场滑去，匀强磁场垂直纸面向里，B ＝0.5T ，从环刚进入磁场算起，到刚好有一半进入磁场时，圆环释放了3.2J 的热量，求：⑴此时圆环中电流的瞬时功率；⑵此时圆环运动的加速度．0.36W ，0.6m/s 2 方向向左5、如图所示，在倾角为θ的光滑斜面上，存在着两个磁感应强度大小相等的匀强磁场，方向一个垂直斜面向上，另一个垂直斜面向下，宽度ef 与fg 均为L.一个质量为m ，边长为L 的正方形线框以速度v 进入上边磁场时，即恰好做匀速直线运动。

拾躲市安息阳光实验学校2011江苏高考物理小一轮复习（假期之友）--电磁感应中的力学问题【知识梳理】1．电磁感应与力学的联系在电磁感应中切割磁感线的导体要运动，感应电流又要受到安培力的作用。

因此，电磁感应问题又往往和力学问题联系在一起，解决电磁感应中的力学问题，一方面要考虑电磁学中的有关规律；另一方面还要考虑力学的有关规律，要将电磁学和力学知识综合起来应用。

电磁感应与动力学、运动学结合的动态分析，思考方法是：电磁感应现象中感应电动势→感应电流→通电导线受安培力→合外力变化→加速度变化→速度变化→感应电动势变化→……周而复始地循环，循环结束时，加速度等于零，导体达到稳定状态．【典型例题】例1：下图中a1b1c1d1 和a2b2c2d2 为同一竖直平面内的金属导轨，处在磁感应强度为B的匀强磁场中，磁场方向垂直导轨所在的平面(纸面)向里。

导轨的a1b1段与a2b2段是竖直的，距离为l1，c1d1与c2d2段也是竖直的，距离为l2．x1y1与x2y2为两根用不可伸长的绝缘轻线相连接的金属杆，质量分别为m1和m2，它们都垂直于导轨并与导轨保持光滑接触。

两杆与导轨构成的回路的总电阻为R。

F为作用于金属杆x1y1上的竖直向上的恒力。

已知两杆运动到图示位置时，已匀速向上运动，求此时作用于两杆的重力的功率的大小和回路电阻上的热功率。

【分析与解】本题是电磁感应现象与物体的平衡相结合的问题，分析中应着重于两个方面，一是分析发生电磁感应回路的结构并计算其电流；二是分析相关物体的受力情况，并根据平衡条件建立方程。

设杆向上运动的速度为v，因杆的运动，两杆与导轨构成的回路的面积减少，从而磁通量也减少．由法拉第电磁感应定律，回路中的感应电动势的大小E = B(l2－l1)v①回路中的电流REI=②电流沿顺时针方向．两金属杆都要受到安培力作用，作用于杆x1y1的安培力为f1 = B l1I③方向向上，作用于杆x2y2的安培力f2 = B l2I④方向向下．当杆做匀速运动时，根据牛顿第二定律有F－m1g－m2g + f1－f2=0 ⑤解以上各式，得)()(1221llBgmmFI-+-=⑥RllBgmmFv212221)()(-+-=⑦作用于两杆的重力的功率的大小P = (m1+m2)gv⑧电阻上的热功率Q =I2R⑨由⑥、⑦、⑧、⑨式，可得gmmRllBgmmFP)()()(21212221+-+-=，RllBgmmFQ21221])()([-+-=。

12专题：电磁感应中的动力学、能量、动量的问题一、电磁感应中的动力学问题1.如图所示，两平行且无限长光滑金属导轨MN、PQ与水平面的夹角为θ＝30°，两导轨之间的距离为L＝1 m，两导轨M、P之间接入电阻R＝0.2 Ω，导轨电阻不计，在abdc区域内有一个方向垂直于两导轨平面向下的磁场Ⅰ，磁感应强度B0＝1 T，磁场的宽度x1＝1 m；在cd连线以下区域有一个方向也垂直于导轨平面向下的磁场Ⅱ，磁感应强度B1＝0.5 T。

一个质量为m＝1 kg的金属棒垂直放在金属导轨上，与导轨接触良好，金属棒的电阻r＝0.2 Ω，若金属棒在离ab连线上端x0处自由释放，则金属棒进入磁场Ⅰ恰好做匀速运动。

金属棒进入磁场Ⅱ后，经过ef时又达到稳定状态，cd与ef之间的距离x2＝8 m。

求：(g取10 m/s2)(1)金属棒在磁场Ⅰ运动的速度大小；(2)金属棒滑过cd位置时的加速度大小；(3)金属棒在磁场Ⅱ中达到稳定状态时的速度大小。

二、电磁感应中的能量问题2.如图甲所示，两条足够长的平行金属导轨间距为0.5 m，固定在倾角为37°的斜面上。

导轨顶端连接一个阻值为1 Ω的电阻。

在MN下方存在方向垂直于斜面向上、大小为1 T的匀强磁场。

质量为0.5 kg的金属棒从AB处由静止开始沿导轨下滑，其运动过程中的v－t图象如图乙所示。

金属棒运动过程中与导轨保持垂直且接触良好，不计金属棒和导轨的电阻，取g＝10 m/s2，sin 37°＝0.6，cos 37°＝0.8。

(1)求金属棒与导轨间的动摩擦因数；(2)求金属棒在磁场中能够达到的最大速率；(3)已知金属棒从进入磁场到速度达到5 m/s时通过电阻的电荷量为1.3 C，求此过程中电阻产生的焦耳热。

三、电磁感应中的动量问题1、动量定理在电磁感应中的应用导体棒或金属框在感应电流所引起的安培力作用下做非匀变速直线运动时，安培力的冲量为：I安＝B I Lt＝BLq ，通过导体棒或金属框的电荷量为：q＝IΔt＝ER 总Δt＝nΔΦΔt·R总Δt＝nΔФR总，磁通量变化量：ΔΦ＝BΔS＝BLx.当题目中涉及速度v、电荷量q、运动时间t、运动位移x时常用动量定理求解．2、正确运用动量守恒定律处理电磁感应中的问题常见情景及解题思路双杆切割式(导轨光滑)杆MN做变减速运动．杆PQ做变加速运动，稳定时，两杆的加速度均为零，以相等的速度匀速运动．系统动量守恒，对其中某杆可用动量定理动力学观点：求加速度能量观点：求焦耳热动量观点：整体动量守恒求末速度，单杆动量定理求冲量、电荷量3.如图所示，光滑平行金属导轨的水平部分处于竖直向下的匀强磁场中，磁感应强度B＝3 T。