2012年学而思杯数学试卷四年级

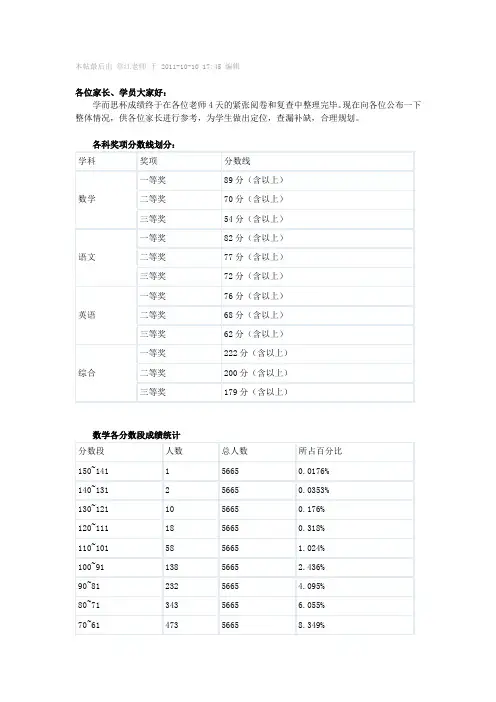
2009年学而思杯 四年级数学试题（A 卷）（时间：60分钟 总分：100分）姓名 准考证号 就读学校 联系电话一、填空题（每题5分，共40分） 1. 计算：20.0931.5 2.009317200.9 3.68⨯+⨯+⨯= ． 2. 我们每次过生日都要吃蛋糕，一般蛋糕上面都要插蜡烛，而且蜡烛数目恰好等于他生日那天的年龄.小明每年过生日都要吃蛋糕，今天又是小明的生日，从出生到今天，他的生日蛋糕共有24根蜡烛，则小明今天过的是____________________岁生日．3. 如图，用水平线或竖直线连结相邻汉字，沿着这些线读下去，正好可以读成“我爱学而思”，那么可读成“我爱学而思”的路线有 条．思而而学学学学爱爱爱爱爱爱我我我我我我我我而学爱我4.两只小蚂蚁同时从图中的A 点出发开始爬向B 点，红蚂蚁沿图中的实线爬行，黑蚂蚁沿图中虚线爬行，如果两只蚂蚁的爬行速度相同，则最先到达B 点的是 ．5.学校为了丰富学生的课余生活，组建了乒乓球俱乐部和篮球俱乐部，同学们踊跃报名参加，其中有321人报名参加乒乓球俱乐部，429人报名参加了篮球俱乐部，但学校最后发现有50人既报名参加了乒乓球俱乐部，又报名参加了篮球俱乐部，还有23人什么俱乐部都没报名，问该学校共有 名学生．6. 67÷所得的小数，小数点后的第2009位数字是 ．7. 把数1，2，3，4，5，6分为三组（不考虑组内数的顺序也不考虑组间的顺序），每组两个数，每组的数之和互不相等且都不等于6，共有____________________种分法．8.小明和小刚清晨来到学校操场练习跑步，学校操场是400米的环形跑道，小刚对小明说：“咱们比比看谁跑的快”，于是两人同时同向起跑，结果10分钟后小明第一次从背后追上小刚，同学们一定知道谁跑得快了，小明的速度是每分钟跑140米，那么如果小明第3次从背后追上小刚时，小刚一共跑了 米．BA二、填空题（每题10分，共60分） 9. 如图，不同的汉字代表不同的数字，其中“变”为1，3，5，7，9，11，13这七个数的平均数，那么“学习改变命运”代表的多位数是 ． 1999998⨯学习改变命运变 10.一般我们都认为手枪指向谁，谁好像是有危险的，下面的规则同学们能看懂吗 规定：警察小偷=警察，警察小偷=小偷．那么：（猎人小兔）（山羊白菜）= ．11. 图中是一个33⨯幻方，满足每行、每列及两条对角线上三数之和都相等，那么其中“★”代表的数是__________．12. 哥哥在过30岁生日时，弟弟说：“等我长到哥哥今年的年龄时，我哥哥那时候的年龄和我今年的年龄之和等于爸爸今年的年龄”，那么爸爸今年的年龄是 岁．13.3月12日植树节，四年级一班同学去植树，如果其中3人各植树2棵，其余每人植树6棵，就恰好植完所有的树苗，如果人数增加到原来的2倍，则每人植树2棵还有8棵树没人植，请问，共有 名学生参加植树，共植树 棵．14.下面是小波和售货员阿姨的一段对话： 小波：“阿姨，您好！”售货员：“同学，你好．想买点什么？”小波：“我只有100元，请帮我安排买10支钢笔和15本笔记本．”售货员：“好，每支钢笔比每本笔记本贵2元，退你5元，请拿好．再见．” 根据这段对话，则钢笔每支是 元，笔记本每本是 元．答题卡。

第八届学而思综合素质测评数学试卷（四年级）考试时间 13:30-15:00 满分100分考生须知：1、 请在答题纸上认真填写考生信息2、 所有答案请填写在答题纸上，否则成绩无效一、填空题（每题5分，共10题，满分50分）1. 计算：2012201310001804880444000_______4÷+÷=。

2. 定义新运算：已知：※满足4※1=15，5※4=21，4※5=11，8※16=48，那么：10※9=_______。

3. 一次数学竞赛满分是100分，某班前六名同学的平均得分是95.5分，排名第六的同学的得分是89分，每人得分是互不相同的整数，那么排名第三的同学至少得_______分。

4. 篮球从高空落下，到达地面后弹起的高度是落下高度的一半，如果篮球从8米的高度落下，那么弹起后再落下，则弹起第_______次时它的弹起高度不足1米。

5.有很多黑的和白的圆形石头。

从中选2个白石和5个黑石按如图所示那样排列。

请问：可以有_______种使白石不相邻的排列方法。

（注意：旋转后两种排列可重合的只算一种）6. 有一个由1，2，3，4，5组成的无重复数字的五位数。

从左起删除第1个数字成为一个四位数时，此四位数是1的倍数；从左起删除第2个数字成为一个四位数的时，此四位数是2的倍数；从左起删除第3个数字成为一个四位数时，此四位数是3的倍数；从左起删除第4个数字成为一个四位数时，此四位数是4的倍数；从左起删除第5个数字成为一个四位数时，此整数是5的倍数。

请写出这样的五位数： _______。

（写出满足题目要求的一种答案即可）7. 小新的生日Patty 上买来许多玩具小火车、玩具小汽车、玩具小飞机、玩具小坦克，每个小朋友任意选择两件，但不能是同样的，问：至少有_______个小朋友去拿，才能保证有两人所拿玩具相同。

8. 小明坐在火车的窗口位置，火车从大桥的南端驶向北端，小明测得共用时间80秒。

2012 年学而思四年级超常班选拔考试一、填空题（每题 7 分，共 28 分）1.计算： 5×2012÷503×15=__________2.某一个等差数列的第 3 项是 14，第 18 项是 23，那么，这个等差数列从第一项到2010 项中有 _______项是整数。

3.如下图，小正六边形沿着大正六边形的边，按顺时针方向滚动。

小正六边形的边长是大正六边形边长的一半。

如果小正六边形沿着大正六边形的边滚动了一周后返回出发时的位置，那么在这个过程中，线段 OA 围着 O 点旋转了 _______圈？OA4.“学学”用写有数字的卡片分别摆出 4 个数（如下图），但是，有部分卡片上的数字被遮挡，已知这 4 个数的平均数是 2012，那么，这 4 个数被遮挡部分的数字之和是 __________□，□ 8，□ 97，□ 825二、填空题（每题 9 分，共 36 分）5.如下图所示，大正方形的边长为 10cm，小正方形的边长为 5cm，那么阴影部分的面积是 ________平方厘米。

6.有长 3 米和 4 米的圆木共 30 根，它们长度的和等于 100 米，现在将它们全部锯成长为 1 米的圆木，如果每次只能锯一块圆木，那么，一共要锯 ____________次。

5 卷到7. 5 本百科全书按从第 1 卷到第 5 卷的递增序号排列，现在要将它们变为反序排列，即从第第 1 卷。

如果每次只能调换相邻的两卷，那么，最少要调换_____________次。

8.一群骗子和一群老实人围成一圈开圆桌会议，老实人只说真话儿，骗子只说假话，每一个老实人两边都是骗子，而每一个骗子两边都是老实人，一个过路人问小明，你们一共有多少人啊？小明说，25 人，那么聪明的小朋友们小明是 _______________? (1)老实人（2）骗子横线上只填序号。

三、填空题（每题 10 分，共 40 分）9.9. 数一数，右图中一共有 ____________个三角形。

2012学而思杯四年级数学真题解析一、填空题(每题7分，共28分)1．我国著名的数学传播、普及和数学竞赛专家单墫教授在2011年“普林斯顿数学竞赛”集训营中，鼓励北京地区参加数学竞赛的小选手，且学且思，作诗一首：“学不思则罔，思不学则殆。

学而思最好，培优创未来。

”已知在“学而思最好，培优创未来”这句话中，不同汉字代表不同数字，那么，“学＋而＋思＋最＋好＋培＋优＋创＋未＋来”的值是___________。

(赵璞铮老师供题)2．算式：34×36＋102×98的计算结果是___________。

(兰海老师供题)3．如图所示，三个正六边形的面积均为6平方厘米，那么，阴影部分的面积是___________平方厘米。

(李萌老师供题)4．学校数学竞赛出了A，B，C三道题，至少做对一道的有25人，其中做对A题的有10人，做对B题的有13人，做对C题的有15人。

如果三道题都做对的只有1人，那么只做对两题的共有___________人。

(曹岚老师供题)二、填空题(每题9分，共36分)5．今天是4月7日，1805年的今天，德国作曲家贝多芬创作的《第三交响曲》在奥地利维也纳剧院首次公演。

作为乐圣，贝多芬一生创作了100多部作品，其中“编号交响曲”9首，“钢琴奏鸣曲”的数量比“小提琴奏鸣曲”的三倍多5首，“小提琴奏鸣曲”的数量比“编号交响曲”多1首。

那么，他一生共创作“钢琴奏鸣曲”___________首。

(魏琦老师供题)6．某天，杨老师去便利店买午饭，便利店当天供应3种不同的荤菜和5种不同的素菜，杨老师打算买2种菜搭配吃，但至少有一种荤菜。

那么，杨老师的午饭共有___________种不同的搭配方式。

(肖京园老师供题)7．摩比、大宽、金儿三人的年龄为3个连续的自然数，摩比年龄最大。

今年他们三人与博士的年龄之和为100岁。

17年后，他们三人的年龄之和恰好等于博士的年龄。

那么，今年摩比___________岁。

2012迎春杯三年级初赛试题一、填空题（每小题8分，共32分）1.计算：928+217+64+8= 。

2.短语“my favorite”中，不同字母表示不同数字，那么m+y+f+a+v+o+r+i+t+e= 。

3.在右图中，四边形ABCD,DEFG均为正方形，已知CE=14,AG=2，那么两个正方形的面积之和是。

4.骆驼有两种：背上只有一个驼峰的单峰骆驼和背上有两个驼峰的双峰骆驼。

单峰骆驼比较高大，四肢较长，在沙漠中能走能跑；双峰骆驼四肢粗短，更适合在沙砾和雪地上行走。

有一群骆驼有23个驼峰，60只脚，那么这群骆驼共有匹。

二、填空题（每小题10分，共40分）5.从1,2,3,4,5,6,7,8,9这是个数字中，选出六个填在下面方框中，使算式成立，一个方框填一个数字，各个方框中所填的数字不相同：□+□□=□□□，那么算式中的三位数最大是。

6.有一类4位数，任意相邻两位数字之和均不大于2，这样的数从小到大排列，倒数第二个是。

7.在右图中，三张大小一样的等边三角形透明玻璃纸，各被分为49个大小相同的小等边三角形，每张玻璃纸上都各有16个小等边三角形涂上了阴影。

如果把这三张玻璃纸重叠在一起，看到的阴影小等边三角形共有个。

8.甲、乙二人相距30米面对面站好。

两人玩“石头剪子布”游戏。

胜者向前走8米，负者向后退5米。

平局两人各向前走1米。

玩了10局后，两人相距7米。

那么两人平了局。

三、填空题（每小题12分，共48分）9.在某天的聚会上，功夫熊猫把手里所有的肉包换成了加菲猫的意大利面，每3个肉包换2份面。

小熊维尼把手里所有的蜂蜜也换成了加菲猫的意大利面，每4罐蜂蜜换5份面。

已知功夫熊猫和小熊维尼换到的意大利面一样多，而且功夫熊猫带的肉包个数与小熊维尼带的蜂蜜罐数相差28，那么加菲猫至少带了份意大利面。

10.30名同学按身高由低到高排成一队。

相邻同学的身高差都相同，前10名同学的身高和是1450厘米。

前20名同学的身高和是3030厘米。

2015年第五届全国学而思综合能力测评（学而思杯）数学试卷（四年级）一．填空题Ⅰ（每题5分，共20分）1. 在下图的两个空白圆圈内填入适当的自然数，使得三角形每条边上三个数的和都相等．那么，左下角的圆圈内应填__________．512【考点】数阵图 【难度】☆ 【答案】3 【分析】略2. 三国时期曹刘大战，曹操派张辽率领精英小分队率先出发．已知张辽一行共36人，张辽自己住1个帐篷，其余人每5人住1个帐篷．那么，一共需要__________个帐篷． 【考点】应用题 【难度】☆ 【答案】8【分析】(361)518-÷+=3. 如图，已知梯形ABCD 中，10CD =，梯形ABCD 的高是4，那么阴影部分的面积是__________．【考点】等积变形、面积公式 【难度】☆ 【答案】20【分析】阴影部分面积即三角形ACD 的面积，104220⨯÷=4. 老师让班上的男生去搬资料．已知资料共有25箱，1名男生一次只能搬1箱；但如果3名男生合作，一次能搬4箱．现在要求一次全部搬完，那么至少需要__________名男生． 【考点】应用题 【难度】☆ 【答案】19 【分析】25461÷=，63119⨯+=二．填空题Ⅱ（每题6分，共24分）5. 佳佳、盛盛、东东三人去买午餐，平均每人花了20元．已知佳佳比盛盛多花了2元，盛盛比东东多花了2元．那么，佳佳花了__________元．【考点】平均数问题 【难度】☆☆ 【答案】22【分析】可以看出，三人所花钱数成等差数列，盛盛就是平均数，20222+=6. 将下面的乘法竖式数字谜补充完整，其中，两个乘数的和是__________．×31【考点】数字谜 【难度】☆☆ 【答案】104【分析】由下面的加法，得到下左图，93193331=⨯=⨯，由于必然进位，最后只能如下右图．19310⨯□□□□□□□931193931023⨯7. 学而思准备成立“滑滑社团”，要求必须至少会滑冰、滑雪中的一项，才有资格成为团员．已知有2015名符合上述要求的人前来报名，其中不会滑冰的有406人，不会滑雪的有460人．那么，其中两种运动都会的有__________人． 【考点】包含与排除 【难度】☆☆ 【答案】1149【分析】20154064601149--=8. 下图中，一共有__________个三角形．【考点】几何计数 【难度】☆☆☆ 【答案】12【分析】53412++=三．填空题Ⅲ（每题7分，共28分）9. 在下图的方格中放入棋子，一个方格中至多能放一枚棋子，并且要求任意两枚棋子不能放在相邻的两格中（有公共边的两格算作相邻）．那么，至多可以放__________枚棋子．【考点】最值问题 【难度】☆☆☆ 【答案】12【分析】12枚构造如图，左右两侧均间隔放置．若放入13枚棋子，注意到左右两侧均只能最多放入6枚，中间放1枚刚好13，但中间一枚和右侧会相邻，所以不能放入13枚或更多棋子．10. 四支足球队进行单循环比赛，即每两个队伍之间都要赛一场．每场比赛，胜者得2分，负者得0分，如果打平则两队各得1分．所有比赛结束后统计四支队伍的得分，发现每支队伍的得分都是偶数，且前两名的得分相同，后两名的得分相同．那么，这四支队伍的得分从高到低组成的四位数是__________． 【考点】体育比赛 【难度】☆☆ 【答案】4422【分析】210计分制总分固定，共有3216++=场比赛，共6212⨯=分，由于不会出现两个满分或两个零分，所以124422=+++．11. 如图，把从1开始的自然数按一定规律排列起来．如果46在这个数表的第a 行，第b 列，那么a b ⨯=__________．…第8列…第 5列第 7列第 6列第 4列第 3列第 2列第 1列第5行第4行第3行第2行第1行…………… (12111098)7654321【考点】方形数表 【难度】☆☆【答案】156【分析】464112÷=，即第12行第2个数，第12行由第12列开始写，所以46在第12行第13列，1213156⨯=．12.用1、2、3、4、8、9这六个数字各一个，组成一个六位数，如果这个六位数能够被1、2、3、4、8、9中的任意一个数字整除．那么，符合要求的六位数有__________个．【考点】整除、计数【难度】☆☆☆☆【答案】84【分析】虽然看上去限制颇多，但实际上由于数字和是12348927+++++=，无论怎么组，必然是3和9的倍数，而8是4、2、1的倍数，只需要满足被8整除即可满足全部条件（但在计数时仍需要逐步思考2、4、8的整除特征）．由2的整除特征，末位必须为偶数，即2、4、8；由4的整除特征，个位是2则十位要是奇数，即12、32、92；个位是4或8则十位要是偶数，即24、84、28、48；由8的整除特征，末两位是12、92、84、28这些不能被8整除的数时，百位是奇数，有+++=种情况；末两位是32、24、48这些能被8整除的数时，百位是偶数，有223310+=种情况；2114++=种情况，共10414末三位定好后前三位随意排布，共1432184⨯⨯⨯=种情况四．填空题Ⅳ（每题8分，共32分）13.一个十位数，满足如下三个条件：①各位数字互不相同；②首位是奇数，且相邻数位数字奇偶性不同；③每个数字（最高位和最低位除外），要么比与它相邻的两个数字都大，要么比与它相邻的两个数字都小．那么，这个十位数的后五位是__________．【考点】逻辑推理【难度】☆☆☆【答案】47698【分析】奇偶间隔，大小呈“波动型”，也就是要么奇数比相邻数大，偶数比相邻数小，要么反之．由于0一定比所有数小，所以一定是奇数比相邻数大，偶数比相邻数小．由于1只比0大，所以1只能放在边上，旁边是0，同理，剩下的数中，3只比2大，所以3只能放在0旁边，再放上2，以此类推，这个十位数只能是103254769814.如图，一个正方形，与4个等腰直角三角形，恰好拼成了一个长方形．如果正方形的面积是16，那么，长方形的面积是__________．【考点】图形分割【难度】☆☆☆【答案】192【分析】图中的三角形都是等腰直角三角形，所以放心大胆图形分割，如图，164(462)192÷⨯⨯⨯=15.五个连续的三位奇数，如果它们的数字和都是质数，那么这五个数的和是__________．【考点】特殊质数【难度】☆☆☆☆【答案】1005【分析】连续奇数差2，则后一个数的数字和要么是前一个数的数字和加2，要么是加2后再减9或减2个9（进一次位数字和少9），所以不难发现，这五个数的数字和必然有3的倍数，所以必有一个数的数字和是3，加2得到5，再加得到7，再加不能得到质数了，这说明这个数前面还有数，而前面的数数字和又不能是1，说明有进位，这个数只能是201或111，前一个数分别是199和109,199数字和是19，前一个197数字和17满足条件，所以这五个数是197、199、201、203、205，和是201的5倍，100516.如图，在一个周长是300米的环形跑道上，甲、乙、丙三人同时从A地出发，甲、乙沿顺时针方向行走，速度分别是每分钟40米和每分钟50米；丙沿逆时针方向行走，速度是每分钟60米．乙每跑100米，就要休息1分钟；甲、丙每次相遇，两人都会同时休息半分钟．那么，当甲第三次超越乙时，丙一共走了__________米．【考点】环形跑道、走走停停【难度】☆☆☆☆【答案】450【分析】300(4060)3÷=，列表÷+=，则甲丙每跑3分钟休息半分钟，100502精细计算，甲分别在乙前三次停时进行了三次超越，当甲第三次超越乙时，甲一共跑了300407.5÷=分钟（甲停丙也停），则丙一共走了7.560450⨯=米五．计算题（每题8分，共16分）17. 计算下列题目，写出简要的计算过程与计算结果：（1）234567222222⨯⨯⨯÷÷ （2）223713-【考点】第五种运算、平方差公式 【难度】☆☆ 【答案】2、1200【分析】（1）2345672345671222222222+++--⨯⨯⨯÷÷===（2）223713(3713)(3713)50241200-=+⨯-=⨯=，或22371313691691200-=-=18. 计算下列题目，写出简要的计算过程与计算结果：（1）4.35 5.30.4355743.5⨯+⨯- （2）()21323x x -+= 【考点】提取公因数、解方程 【难度】☆☆ 【答案】4.35、5x =【分析】（1）4.35 5.30.4355743.5 4.35(5.3 5.710) 4.351 4.35⨯+⨯-=⨯+-=⨯= 或4.35 5.30.4355743.523.05524.79543.5 4.35⨯+⨯-=+-= （2）()21323223235255x x x x x x -+=⇒-+=⇒=⇒=六．解答题（每题15分，共30分）19. 磁悬浮列车是一种依靠磁力来驱动的列车，由于不需要接触地面，因此速度极快．已知一列磁悬浮列车的速度是每秒120米．回答下列问题：（1）该列车完全通过轨道旁的一根电线杆只用了 2.5秒，请问：该列车车身长度是多少米？（5分）（2）该列车完全通过一条长度是420米的隧道，需要多少秒？（5分）（3）俊俊骑自行车在轨道旁匀速行驶，该列车从俊俊的后方驶来．从列车车头追上俊俊，到车尾离开俊俊，共用时3秒．请问：俊俊骑自行车速度是每秒多少米？（自行车长度忽略不计）（5分） 【考点】火车过桥 【难度】☆☆ 【答案】300、6、20【分析】（1）120 2.5300⨯=米 （2）(420300)1206+÷=秒 （3）120300320-÷=米/秒20. 定义新运算“⊗”：a b ⊗表示整数a 与整数b 的乘积去掉后两位所形成的数（请注意：当100a b ⨯<时，或者a 、b 不是整数时，a 、b 不能使用“⊗”运算）． 例如：因为1360780⨯=，所以13607⊗=．回答下列问题：（1）计算1799⊗；（3分）（2）如果m m m ⊗=，请求出整数m 的最小值；（6分） （3）如果x y x y ⊗=-，请求出x y +的最小值．（6分） 【考点】定义新运算、最值问题 【难度】☆☆☆☆ 【答案】16、100、21【分析】（1）17991683⨯=，所以179916⊗=（2）需要m m ⨯大小至少是00m ，即100m ，所以最小是100100100⊗=（3）两个数差越小，即越接近，其“新运算”的结果越小，乘积就会小，乘积小、差也小，和就必然较小．注意定义中说到乘积小于100不能运算，则差最小是1，所以尝试1x y ⊗=，即乘积是100多、差是1的两个数，那么1110110⨯=，满足条件，两数和为21由于和一定差小积大，显然和是20且不相等（差不能是0）的两个整数乘积都小于1010100⨯=，不能满足情况，当然和更小的也一定不会满足，所以x y +最小值为21。

2013年第三届全国学而思综合能力测评（学而思杯）数学试卷（四年级）详解一．1.填空题（每题5分，共20分）请计算：3、5、7、9、11、13这6个数的平均数是__________．【考点】计算，平均数【难度】☆【答案】8【分析】公式法：(3?5?7?9?11?13)?6?8；或移多补少找到平均值8.2.在一个神奇的地方，有一排奇怪的雕塑，这些雕塑都是由巧克力构成的，第一个雕塑由3块巧克力组成，第二个雕塑由6块巧克力组成，第三个雕塑由9块巧克力组成，以此类推，每个雕塑都比前一个多3块巧克力．那么，第__________个雕塑恰好由2013个巧克力组成．【考点】计算，数列【难度】☆【答案】671【分析】第n个雕塑由3n块巧克力构成，故由2013块巧克力构成的是第2013?3?671个雕塑.3.右图中，相邻两个格点的距离为1，那么阴影部分的面积是__________【考点】几何，格点与割补【难度】☆☆【答案】12【分析】可使用毕克公式直接求出：9?8?2?1?12；或使用分割的方法，阴影部分面积为：(2?2?2)?4?2?2?12.4.右图中，共有__________个三角形．【考点】组合，几何计数【难度】☆☆【答案】8【分析】单个三角形有4个，由2个三角形组成的三角形有3个，由4个三角形组成的三角形有1个.1二．5.填空题（每题6分，共24分）如右图，算式中不同的汉字代表不同的数字，已知：“级=5”，那么“学而思”代表的三位数是__________．【考点】数字谜【难度】☆☆【答案】892【分析】“更”=1，故“进”=0；十位必然向百位进位了，故“学”=8，进而“而”=9；此时可知个位没有向十位进位，思?5?步”只能为“2?5?7”“；综上，答案为892.6.4月有30天．某年4月有5个星期一，5个星期日，如图，在该月日历表上用“__________．”圈出5个数，并计算出它们的和，和最大是【考点】计算，数表，日历问题【难度】☆☆【答案】115【分析】十字形越靠下，圈住的数之和越大；由已知条件易得这个月的30日是周一，故当十字圈住30、24、23、22、16日时，可得到最大和，为30?24?23?22?16?23?5?115.7.如果3m?31?33?35?37?39，那么m=__________．【考点】计算，乘方运算【难度】☆☆【答案】25【分析】同底数幂相乘，底数不变，指数相加；31?33?35?37?39?31?3?5?7?9?325，故m?25.8.甲、乙、丙三人读同一本故事书，这本故事书里一共有100个故事，甲已经读了70个故事，乙已经读了60个故事，丙已经读了50个故事，则恰好被甲乙丙3人中两人读过的故事最多有__________个．【考点】组合，构造与论证【难度】☆☆☆【答案】90【分析】三人共读了50?60?70?180个故事（有重复）；故被读了2遍的故事理论上的最大值为180?2?90；下面构造一种看书方法，来证明90可以达到：把故事编为1～100号，甲读1～70号，乙读71～90号以及1～40号，丙读41～90号；这样1～90号故事都是恰被两人读过；综上，答案为90.2三．9.填空题（每题7分，共28分）如右图，正方形ABCD 的边长为12厘米，正方形DEFG的边长为8厘米，H 是正方形DEFG的中心（对角线的交点），那么，阴影部分的面积是__________平方厘米．AEHD【考点】几何，面积【难度】☆☆☆【答案】24【分析】把图形分为方格阵，每个小方格边长4厘米，并设FG与AC的交点为M点，如右图；现在已可用毕克公式或割补的方法来求阴影面积了；毕克公式：(4?4)?(0?5?2?1)?24平方厘米；分割：S阴影?S△HMA?S△HMC?4?8?2?4?4?2?24平方厘米；整体减空白：12?12?2?4?4?4?8?2?2?24平方厘米.BABFGCEHGCDFM10.定义：a?ba?ba?bb2，那么下面算式的计算结果为__________．10?1?10?2?10?3?10?4?10?5?10?6?10?7?10?8?10? 9?10?10【考点】计算，定义新运算，平方差公式【难度】☆☆【答案】1000【分析】由平方差公式：a?ba?ba?bb2?a2?b2?b2?a2，2故原式?102?102?1022?100?10?1000.?10?10?10个10211.甲、乙两人分别从A、B两地同时出发，相向而行．如果乙每分钟行20米，甲、乙两人5分钟后相遇；如果乙每分钟比原来快4米，甲、乙两人在A、B两地中点相遇．那么，A、B两地相距__________米．【考点】行程问题，相遇问题【难度】☆☆【答案】220【分析】第二次走路，两人相遇在中点，说明两人速度相同，为20?4?24米每分；故在第一次走路时，甲速为24米每分，乙速为20米每分，两人5分钟后相遇，故全长为(20?24)?5?220米.312.有形状、长短都完全一样的红筷子、黑筷子、白筷子各25根．在黑暗中，至少应摸出__________根筷子，才能保证摸出的筷子至少有8双（每两根同色的筷子视为1双）．【考点】组合，抽屉原理和最不利原则【难度】☆☆☆【答案】18【分析】摸出7双筷子之后，又把三种颜色的筷子各摸出1根，此时已摸出2?7?3?17根筷子，但没有摸出8双，这是最不利情况；之后无论摸出哪根筷子，都将摸出8双筷子，故答案为17?1?18.四．填空题（每题8分，共32分）13.将1至5分别填入图中的圆圈内，使得两条线段上3个数的和相等．那么，共有__________种不同的填法．【考点】组合，数阵图【难度】☆☆☆【答案】24【分析】数和为15，故15加中心数等于线和的2倍，可知中心数只能为奇数，有3种选择；中心数222填好后，两组数可互换左右，各组内也可互换位置；故答案为3?A2?A2?A2?24种.14.阿凡提在地主家做长工．地主家有一根长为20尺的木头，阿凡提每次将木头锯成长度是整数尺的两段，并计算这两段长度的乘积．最后，阿凡提将木头锯成20段长度是1尺的小段，并得到了19个乘积，他将这些乘积相加得到1个数A，地主会给他A个金币做为工资．那么，A等于__________．【考点】操作类问题【难度】☆☆☆【答案】190【分析】可先使用一种特殊方法算出A的值，比如每次切下1尺，那么19个乘积之和为1?19?1?18?1?2?1?1?190；下证无论如何分割，A值为190不变：方法一：找规律：2尺的木头A?1不变，3尺的木头A?3不变，4尺的木头A?6不变，5尺的木头A?10不变，……，20尺的木头A?190不变（可用第二数学归纳法严谨证明通项公式为；n(n?1)?2，但小学阶段只要找到规律即可）方法二：转化问题：20个人每轮分两组握手，每一轮握手之后，组内再分成两组，互相握手，直至每组最后一轮握手时组内都只有1个人，求总握手次数；组与组之间的握手次数正是两组人数相乘，故这个问题的结果与题目的结果相同，但这个握手问题其实就是每两人都握了一次手，2故结果是C20?190，故A?190；4方法三：数形结合：如下图，分割木头方法对应分割图形面积的方法，乘积对应矩形面积，可见无论如何分割，结果都是1?2?3?19?190.15.甲、乙、丙3人在周长是300米的环形跑道上同时同地同向出发．甲第一次追上乙时，甲、乙恰好都回到出发点，此时丙距离出发点100米；过了一会，甲第一次追上丙时，乙跑了7圈多一些．那么，丙第一次追上乙时，甲总共跑了__________米．【考点】行程问题，环形跑道问题【难度】☆☆☆☆☆【答案】5400【分析】“丙距离出发点100米”和“乙跑了7圈多一点”是本题的关键突破口；甲要追丙1圈300米，才能第一次追上丙，“丙距离出发点100米”说明甲追了丙100米或200米（分别对应丙在出发点之后100米和丙在出发点之前100米），但若只追了100米，则甲还要跑目前圈数的2倍才能追上丙，同时乙也将跑2倍圈数，即乙将跑整数圈，就不会出现“乙跑了7圈多一点”了；这说明甲乙碰面时，甲已经领先丙200米；这说明乙又跑了（甲已碰面时）已跑的圈数的一半后，出现“乙跑了7圈多一点”，故“7圈多一点”为7.5圈；故甲追上乙时，乙跑了5圈1500米，甲跑了6圈1800米，丙跑了1800?200?1600米，故甲、乙、丙的速度比为1800:1500:1600?18:15:16；故丙追上乙时，丙跑了16圈，乙跑了15圈，甲跑了18圈5400米.516.A、B、C、D四个队进行循环赛，即每两个队都比赛一场，每场比赛中，胜队得3分，负队得0分，平局则各得1分，每个队只知道自己3场比赛的情况．裁判说：你们的得分互不相同；A说：虽然我不知道你们的得分，但我肯定是第一；B说：那我一定是第二，而且我知道A得了多少分；C说：A说话之前我就知道我是第三．根据以上信息，这四个队的得分从高到低组成的四位数是__________．【考点】组合，体育比赛中的数学问题【难度】☆☆☆☆☆【答案】7531【分析】先考虑C：可构造出7431，及5432，故知4分（1胜1平1负）可能得第二，2分（2平1负）可能得第四，所以C 必为3分；再考虑A：若ABCD的得分为5432，则A1胜2平不可能断定自己是第一，故不是5432，A要得到7分或9分才可断定自己是第一；再考虑B：若B为6分（2胜1负），则B一定输给A，但无法断定ABCD是9630还是7631（即B不能知道A的分数），故B不是6分，B是5分或4分；下证B不可能是4分：若B得4分（1胜1平1负），其中若B与A平，则B可由A的话推知A胜了C、D，此时B会考虑ABCD有可能是7460或7406，故B无法断定自己是第二；若B输给A，则B 会考虑ABCD有可能是7450或7405，故B无法断定自己是第二；综上，若B是4分，则无法断定自己是第二；故B得5分（1胜2平），听到A的话后能断定自己第二；再重新考虑A：A已经不可能是全胜战绩了，故A 得7分（2胜1平）；综上，答案为7531.6五．解答题（每题8分，共16分17.计算：（1）1.1?9.1?0.8?12.5?0.3?0.4（4分）（2）333333333?6?999999999（4分）【考点】计算，巧算【难度】☆☆【答案】20.13；2【分析】（1）原式?10.01?10?0.12?20.13；（2）原式?333333333?6?333333333?3?6?3?2.18.解方程：（1）3(2x?1)?4?7（4分）（2）5(x?3)?2(x?2)?4（4分）【考点】计算，解整系数方程【难度】☆☆【答案】x?1；x?5【分析】（1）原方程化为6x?3?4?7，即6x?6，解得x?1；（2）原方程化为5x?15?2x?4?4，即3x?15，解得x?5；要注意去第二个括号时要变号.六．解答题（每题15分，共30分）19.今年是公元2013年．观察2013这个数，它是由四个连续的自然数组成的四位数．我们将满足这样条件的年份称为“如意年”．（1）下一个“如意年”，是公元哪一年？（5分）（2）从公元1000年到公元2012年，共经历了多少个“如意年”？（10分）【考点】组合，加乘原理，枚举法【难度】☆☆☆【答案】2031年；12个【分析】（1）若要保持“20”打头，则年份必由0、1、2、3组成，2013之后，下一个是2031最近；（2）“1”打头的“如意年”，后三位数字可能是0、2、3，也可能是2、3、4；两种情况分别3有A3?6种，故共有6?6?12种，枚举如下：1023、1032、1203、1230、1302、1320、1234、1243、1324、1342、1423、1432；“2”打头的如意年最小就是2013年，但题目要求到2012年，故知“2”打头的没有；综上，答案为12种720.如图，除仓库外每个点均表示一家客户．学学从仓库出门送鱼．他从仓库的保鲜柜中每取出一家的鱼后（取鱼时间忽略不计），装车时间是5分钟，相邻两家客户间的驾车时间是5分钟，从学学将鱼送到客户家到将鱼装进客户家保鲜柜中的时间也是5分钟．另外，如果鱼在保鲜柜外的时间超过60分钟，就会不新鲜．（1）学学从取鱼开始，到将鱼送到A家的保鲜柜中，需要多少分钟？（2分）（2）如果保证客户能吃上新鲜的鱼，学学每次最多送几家？（5分）（3）如果保证图中所有客户都能吃上新鲜的鱼，那么学学送完所有的鱼并回到仓库最少需要多少分钟？（8分）【考点】操作类问题【难度】☆☆☆☆☆【答案】15分钟；5家；260分钟【分析】（1）装车、走路、装保鲜柜共用5?5?5?15分钟；（2）每一家走路、装保鲜柜都至少5?5?10分钟；且最远的那一家，在装车时即使最后装，5（分钟）还未出发时也以离开保鲜柜5分钟了；故一次最多运(60?5)?10?5（家）；仓库A（3）由于每次最多运5家，故至少要运3次；14家鱼店的装车和装保鲜柜，必然用去14?(5?5)?140分钟；剩下的工作是：只需走的路线为最短即可，最短也要走6?10?8?24段路（左边5家至少6段路，右上角一家至少10段路，其余部分至少8段路；举例如下图，例子不唯一），花24?5?120（分钟）；至少共用140?120?260（分钟）.仓库A（例子：先按左边的普通箭头送5家，走6段路；再按虚线箭头送5家，原路返回，走10段路；最后按粗箭头送4家，走8段路，共走24段路）8。