同济大学2006结构力学考研真题
- 格式:pdf
- 大小:271.75 KB
- 文档页数:7
第1节 静定平面桁架一、桁架的内力计算方法1、结点法取结点为隔离体,建立平衡方程求解的方法,每个结点最多只能含有两个未知力。
该法最适用于计算简单桁架。
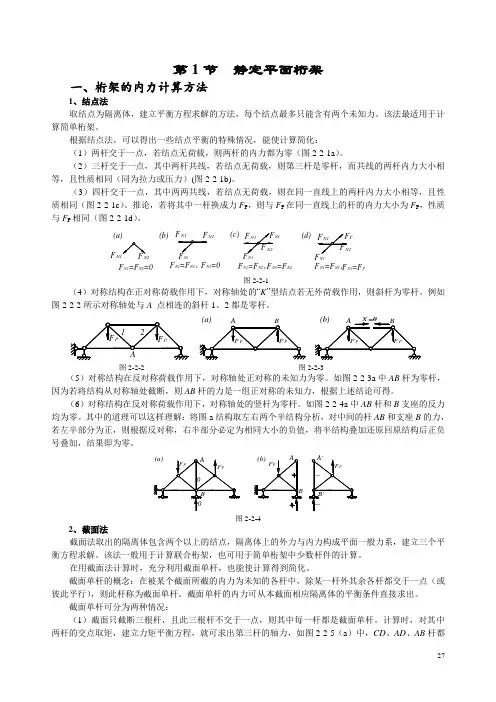
根据结点法,可以得出一些结点平衡的特殊情况,能使计算简化:(1)两杆交于一点,若结点无荷载,则两杆的内力都为零(图2-2-1a )。
(2)三杆交于一点,其中两杆共线,若结点无荷载,则第三杆是零杆,而共线的两杆内力大小相等,且性质相同(同为拉力或压力)(图2-2-1b)。
(3)四杆交于一点,其中两两共线,若结点无荷载,则在同一直线上的两杆内力大小相等,且性质相同(图2-2-1c )。
推论,若将其中一杆换成力F P ,则与F P 在同一直线上的杆的内力大小为F P ,性质与F P 相同(图2-2-1d )。
F N3F N3=0F N1=F N2=0F N3=F N4(a)(b)(c)F N4(d)F N3=F PF PN1F F N2F N1F N2F N1F N2F N1F N2F N3F N3F N1=F N2,F N1=F N2,F N1=F N2,图2-2-1(4)对称结构在正对称荷载作用下,对称轴处的“K ”型结点若无外荷载作用,则斜杆为零杆。
例如图2-2-2所示对称轴处与A 点相连的斜杆1、2都是零杆。
1A2F PF PAF PF PBF PF PBA(b)(a)X =0图2-2-2 图2-2-3(5)对称结构在反对称荷载作用下,对称轴处正对称的未知力为零。
如图2-2-3a 中AB 杆为零杆,因为若将结构从对称轴处截断,则AB 杆的力是一组正对称的未知力,根据上述结论可得。
(6)对称结构在反对称荷载作用下,对称轴处的竖杆为零杆。
如图2-2-4a 中AB 杆和B 支座的反力均为零。
其中的道理可以这样理解:将图a 结构取左右两个半结构分析,对中间的杆AB 和支座B 的力,若左半部分为正,则根据反对称,右半部分必定为相同大小的负值,将半结构叠加还原回原结构后正负号叠加,结果即为零。
结构力学1.写出你所学过的或阅读过的结构力学的各章章名。
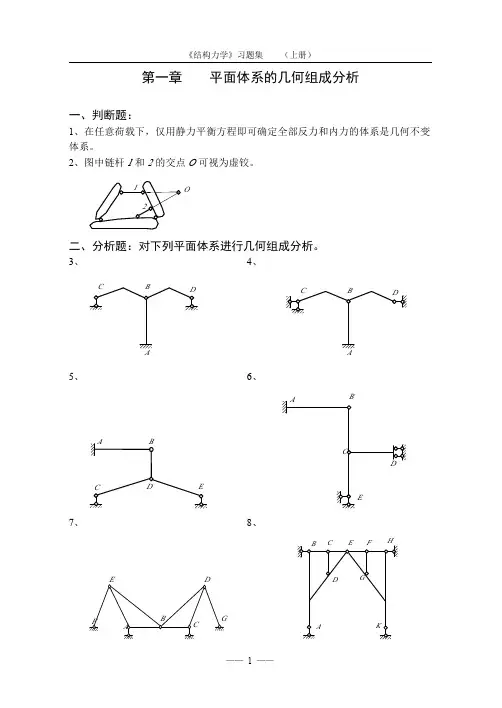
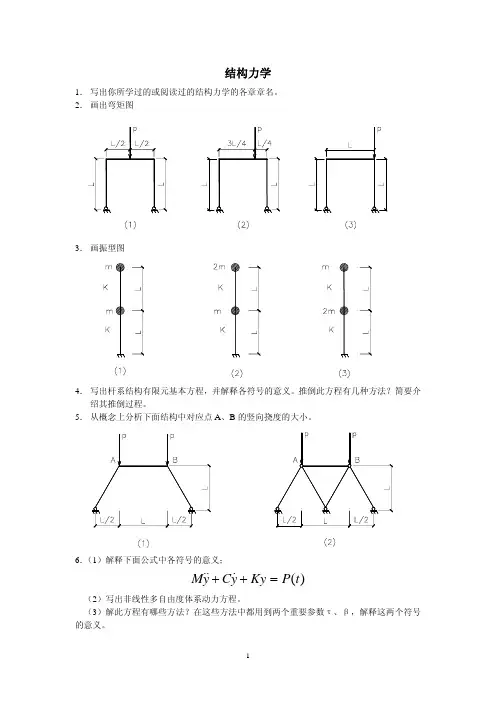
2.画出弯矩图3.画振型图4.写出杆系结构有限元基本方程,并解释各符号的意义。
推倒此方程有几种方法?简要介绍其推倒过程。
5.从概念上分析下面结构中对应点A、B的竖向挠度的大小。
6.(1)解释下面公式中各符号的意义;M=+y+)(tCKyPy(2)写出非线性多自由度体系动力方程。
(3)解此方程有哪些方法?在这些方法中都用到两个重要参数τ、β,解释这两个符号的意义。
7.画出下列二结构的振型图,并说明有何异同点。
8.桥梁中有哪些动力问题?9.高墩和矮墩的抗震破坏形式。
10.桥梁工程中数值计算方法有哪些?11.有限元、有限条法的基本概念。
14.有一种原始的斜拉桥,结构图式如下,试分析此结构是否为斜拉桥体系,若不是,是什么体系结构?说出理由。
18.跨江、河大桥的设计中应注意哪些问题?19.画振型图。
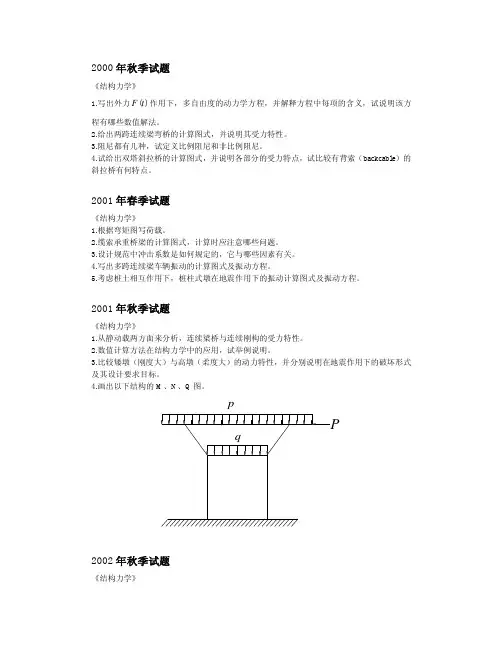
20. 如下图,1) 两梁跨度均为l,若两者跨中挠度相同,则两荷载间有何关系?2) 画出两梁的剪力图、弯矩图。
3) 从中你可得出何力学概念?21. 何为第一、二类稳定问题?何为结构失稳?两者有什么不同?试举例说明。
22. 桥梁设计中有哪些动力学问题?22.叙述房屋结构和桥梁结构荷载作用特点,从数学和物理的观点分析。
23.画空间杆的弯矩、扭矩、剪力图。
24. 写出结构动力学的主要内容。
25.简述建筑结构和桥梁一般承受什么类型的荷载,试从数学和力学的观点,分析这些荷载的性质。
!!!!!!!!!!重在扩展,本人认为同济考题重基础运用,重灵活总结:以上25题,结力11题,动力学9题,结力延伸题6题。
结力包括章节名,内力图(平面超静定或空间静定),位移判断,稳定概念,荷载。
动力学包括振型图及其分析,周期比较,动力方程,动力问题概念(如综述或列举),抗震。
结力延伸题包括数值方法(有限元,有限条等),大跨桥梁设计问题。
桥梁结构理论1.写出斜拉桥结构体系(静力和动力)的特点。

2000年秋季试题《结构力学》F t作用下,多自由度的动力学方程,并解释方程中每项的含义,试说明该方1.写出外力()程有哪些数值解法。
2.给出两跨连续梁弯桥的计算图式,并说明其受力特性。
3.阻尼都有几种,试定义比例阻尼和非比例阻尼。
4.试给出双塔斜拉桥的计算图式,并说明各部分的受力特点,试比较有背索(backcable)的斜拉桥有何特点。
2001年春季试题《结构力学》1.根据弯矩图写荷载。
2.缆索承重桥梁的计算图式,计算时应注意哪些问题。
3.设计规范中冲击系数是如何规定的,它与哪些因素有关。
4.写出多跨连续梁车辆振动的计算图式及振动方程。
5.考虑桩土相互作用下,桩柱式墩在地震作用下的振动计算图式及振动方程。
2001年秋季试题《结构力学》1.请写出有限元的基本方程,该方程有三种理论可得到,请写出这三种理论并作简要说明及介绍。
2.有限元计算的动力方程为[]{}[]{}[]{}{}M uC u K u R ++=&&& (1)说明方程中各符号的意义;(2)写出非线性动力平衡方程的增量表达式,并解释各符号代表的意义。
(3)该增量方程最常用的数值解法是逐步积分法,其逐步积分法到底包括哪几种方法,2003年秋季试题《结构力学》1.(1)画出图中结构的Q 、M 图,()sinq x q x lπ= (2)两结构跨中挠度相等时,P 与q 的关系。
(3)请给出结构失稳(杆件系统)的例子。
3.在桥梁设计中应考虑哪些动力问题。
2004年试题2004年试题1.试从数学、力学角度分析建筑和桥梁结构上作用荷载的异同。
2.空间静定刚架弯矩、剪力、扭矩图。
3.试用最简洁的语言概述结构动力学的主要内容。
2005年试题1 画A、B截面的影响线。
A BA B2 已知右拱脚水平位移为x ∆,竖向位移为y ∆。
(1)求右侧3,84l l 处拱截面的竖向位移, (2)求水平推力影响线。
3 使1~7点竖向位移为0,8点处水平位移为0,塔底弯矩为0的调索方程。
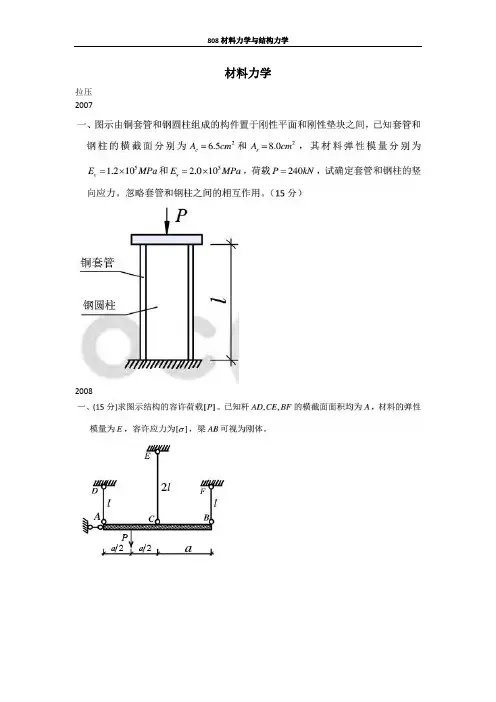
材料力学拉压2007200820102011二、如图所示杆系结构中,各杆EA均相同,许用拉应力均为[σ],试求:(1)、当A点处作用竖向力F P时,求F P的最大值;(2)、若已知AB杆哎制造时比原尺寸长∆,求各杆初始应力。
一、图示结构AB杆为实心圆杆,其截面抗扭刚度为GI P;CD杆为刚性杆,竖杆CF、DH位于与平面yAz平行的同一平面内,其截面轴向刚度为EA。
已知绕x轴的力矩Mx作用在B 结点处,试求CF、DH杆的轴力以及AB杆所受的扭矩。
扭转20072008200920102011平面弯曲、应力状态、强度理论、组合变形200720082009四、图示工字钢制成的简支梁,腹板位于竖直平面内,截面高度为25cm,翼缘宽度和厚度各为11.8cm和 1.3cm,腹板厚度为1cm。
材料的容许正应力[σ]=160MPa,容许剪应力[τ]=100MPa,试用第三强度理论对该梁进行强度校核。
五、截面半径为R的圆直杆AB和BC在水平面内,A端固定,AB与BC刚接且相互垂直,弹性模量为E,泊松比为ν。
通过C截面形心,垂直于BC杆张拉一根拉锁CD,CD与y方向成θ角。
测得H截面g点处沿x正方向的线应变为ε0。
试求:(1)拉索的张力N CD;(2)H截面h 点处,在杆件表面上与x正方向和y正方向均成45°角的线应变ε45°。
2010二、根据弯矩、剪力、荷载间的关系作出图示多跨静定梁的剪力图和弯矩图。
四、如图所示,悬臂梁截面为矩形b×h=90×180,承受荷载,,悬臂梁材料的弹性模量E=10GPa,试求:(1)梁内最大x向正应力及其作用点位置;(2)梁的最大转角;(3)梁矩形截面的截面核心。
五、弹性体内某点的应力状态为平面应力状态,如图所示,,,,材料的弹性模量为E=210GPa,泊松比为v=0.3。
(1)试用解析法求该点的主应力,并画出主应力单元体;(2)求该点的最大剪应力;(3)求该点的主应变。

2001年研究生入学考试桥梁工程试题一、简答题1. 无腹筋梁在斜裂缝出现前后,梁内应力状态有何变化?2. 试叙述预应力混凝土结构的基本原理。
3. 与梁式桥相比,拱桥有哪些特点?拱中水平推力的大小主要取决于对哪些因素?4. 如何处理拱桥中的不等跨分孔问题?二、计算题1. 已知某单筋矩形截面梁b=25cm,h=50cm,受弯构件承受计算弯矩Mj=100kNm,采用25号混凝土和Ⅱ级钢筋(Ra=14.5MPa、Rg=340MPa),相应混凝土受压区高度界限系数ξjg=0.55,材料安全系数γc=γs=1.25。
如果设ag=4cm,计算所需受拉钢筋面积。
2. 钢筋混凝土偏心受压构件,b=40cm,h=60cm,计算长度l0=6m。
采用20号混凝土和Ⅱ级钢筋(Ra=11MPa、Rg=340MPa),Ag=12.56cm2,A′g=15.2cm2,ag=a′g=4cm,混凝土受压区高度界限系数ξjg=0.5,材料安全系数γc=γs=1.25,γb=0.95。
承受轴向压力Nj=1000kN,计算弯矩Mj=303.4kNm,偏心距增大系数η=1.105,验算在弯矩作用平面内是否满足纵向承载力的要求2002年研究生入学考试桥梁工程试题一、简答题1.无腹筋梁当斜裂缝出现后,截面中钢筋和混凝土的应力状态与斜裂缝出现前相比有什么变化?2.比较普通股筋柱与螺旋箍筋柱中箍筋的作用,并从轴向力应变曲线说明螺旋箍筋柱的受压承载力和延性均比普通箍筋柱高。
3.车轮荷载在行车道板上的分布是如何处理的?4.布置多跨梁桥的固定支座和活动支座时一般要考虑哪些原则?5.混凝土的弹性模量Eh如何测定?它和变形模量E″h有何区别?两者有何关系?6.写出计算正常使用极限状态时,常见的几种荷载效应组合。
7.采用偏心距增大系数η的作用是什么?什么情况下可不计η?8.截面效率指标的定义及其意义。
二、计算题一座变截面无铰拱桥,跨径l=40m,矢跨比f/l=1/8,拱轴线为二次抛物线y=4fx2/l2,主拱圈为钢筋混凝土板拱,整体浇筑,混凝土标号为40号(弹性模量E=3.3×104MPa),拱顶截面高1.0m,宽8.0m,截面惯矩按Ii=Id/cos 规律变化。
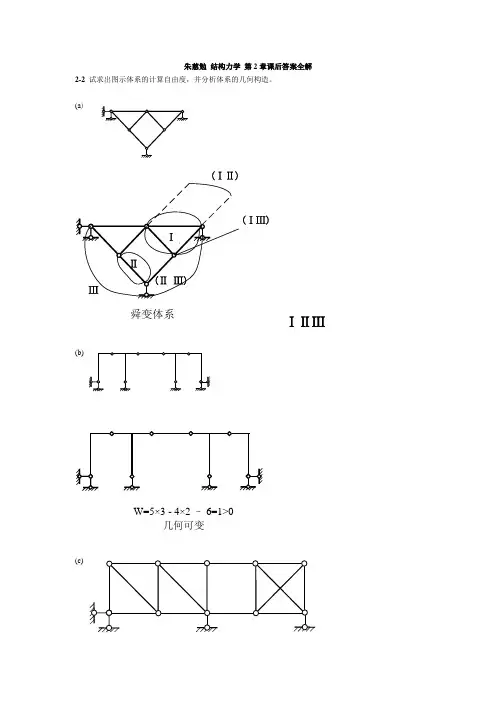
朱慈勉 结构力学 第2章课后答案全解2-2 试求出图示体系的计算自由度,并分析体系的几何构造。
(a )ⅠⅡⅢ(ⅠⅡ)(ⅠⅢ)(Ⅱ Ⅲ)舜变体系`ⅠⅡⅢ(b)W=5×3 - 4×2 – 6=1>0几何可变(c)有一个多余约束的几何不变体系(d)2-3 试分析图示体系的几何构造。
(a)(ⅠⅢ)ⅠⅡⅢ(ⅠⅡ)(Ⅱ Ⅲ)几何不变W=3×3 - 2×2 – 4=1>0可变体系ⅠⅡⅢ(ⅠⅡ)(ⅠⅢ)(ⅡⅢ)几何不变2-4 试分析图示体系的几何构造。
(a)(ⅠⅢ)(ⅠⅡ)(ⅡⅢ)ⅠⅡⅢ几何不变(b)W=4×3 -3×2 -5=1>0几何可变体系ⅢⅠⅡ(ⅠⅢ)(ⅡⅢ)(ⅠⅡ)几何不变(d)(ⅠⅡ)ⅢⅠⅡ(ⅡⅢ)(ⅠⅢ)二元杆有一个多余约束的几何不变体ⅠⅡⅢ(ⅠⅢ)(ⅡⅢ)(ⅠⅡ)舜变体系(f)ⅠⅡⅢ(ⅠⅢ)(ⅡⅢ)(ⅠⅡ)无多余约束内部几何不变ⅠⅡⅢ(ⅠⅢ)(ⅠⅡ)(ⅡⅢ)二元体(h)ⅠⅡⅢ(ⅠⅢ)(ⅠⅡ)(ⅡⅢ)二元体多余约束W=3×8 - 9×2 – 7= -1, 有1个多余约束2-5 试从两种不同的角度分析图示体系的几何构造。
(a)(ⅠⅢ)ⅠⅡⅢ(ⅠⅡ)(ⅡⅢ)舜变体系(b)ⅠⅡⅢ(ⅠⅡ)(ⅡⅢ)(ⅠⅢ)几何不变同济大学朱慈勉 结构力学 第3章习题答案3-2 试作图示多跨静定梁的弯矩图和剪力图。
(a)4P F a2P F a 2P F a M4P F Q34P F 2P F(b)ABCaa aaaF P a DEFF P2m6m2m4m2mABCD10kN2kN/m42020M Q10/326/3410(c)21018018040M1560704040Q(d)3m2m2mA B CEF15kN 3m3m4m20kN/mD 3m2m2m2mA2m 2m2mABCD E FG H 6kN ·m4kN ·m 4kN2m7.5514482.524MQ3-3 试作图示刚架的内力图。

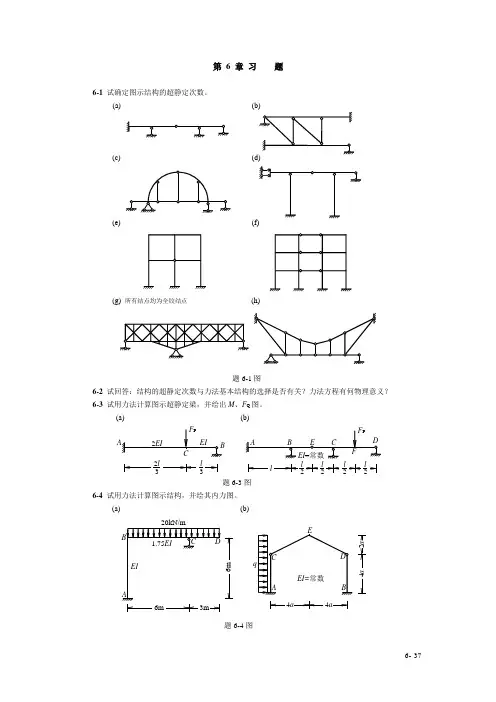
6- 37第 6 章 习 题6-1 试确定图示结构的超静定次数。
(a) (b)(c)(e)(g) 所有结点均为全铰结点(h)题6-1图6-2 试回答:结构的超静定次数与力法基本结构的选择是否有关?力法方程有何物理意义? 6-3 试用力法计算图示超静定梁,并绘出M 、F Q 图。
(a) (b)题6-3图6-4 试用力法计算图示结构,并绘其内力图。
(a)(b)题6-4图4a 2a4a4a3m6m6m2l 3l 3l2l 2 l2ll 26- 386-5 试用力法计算图示结构,并绘出M 图。
(b) (c) (d)题6-5图6-6 试用力法求解图示超静定桁架,并计算1、2杆的内力。
设各杆的EA 均相同。
(a)(b)题6-6图6-7 试用力法计算图示组合结构,求出链杆轴力并绘出M 图。
(a) (b)题6-7图6-8 试利用对称性计算图示结构,并绘出M 图。
6m6m3m3m6m6maaa1.5m6m3m6m3ml la aaa6- 39(a) (b) (c) (d)(e) (f)( BEH 杆弯曲刚度为2EI ,其余各杆为EI )(g) (h)题6-8图6-9 试回答:用力法求解超静定结构时应如何恰当地选取基本结构? 6-10 试绘出图示结构因支座移动产生的弯矩图。
设各杆EI 相同。
(a)hll ll3m4m5m4m60kNA BC DEI=常数llAB CDEI=常数qqlllDEAB EI=常数qqC Faaa2a 2aaaaaa6m 6m 9m2l2l 2 l l6- 40(b)题6-10图6-11 试绘出图示结构因温度变化产生的M 图。
已知各杆截面为矩形,EI=常数,截面高度h=l/10,材料线膨胀系数为α。
(a) (b)题6-11图6-12 图示平面链杆系各杆l 及EA 均相同,杆AB 的制作长度短了 ,现将其拉伸(在弹性范围内)拼装就位,试求该杆轴力和长度。
题6-12图 题6-13图6-13 刚架各杆正交于结点,荷载垂直于结构平面,各杆为相同圆形截面,G = 0.4 E ,试作弯矩图和扭矩图。