2005年同济大学结构力学考研试题
- 格式:pdf
- 大小:325.08 KB
- 文档页数:5
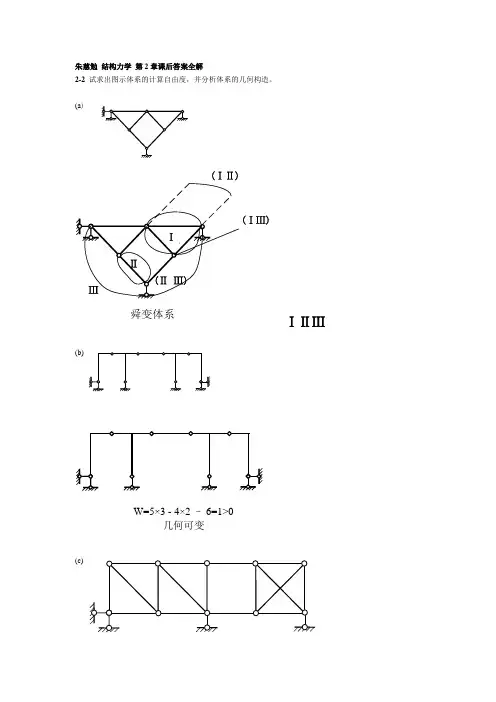
朱慈勉 结构力学 第2章课后答案全解2-2 试求出图示体系的计算自由度,并分析体系的几何构造。
(a )(ⅠⅡ)(ⅠⅢ)舜变体系ⅠⅡⅢ(b)W=5×3 - 4×2 – 6=1>0几何可变(c)有一个多余约束的几何不变体系(d)W=3×3 - 2×2 – 4=1>0可变体系2-3 试分析图示体系的几何构造。
(a)(ⅡⅢ)Ⅲ几何不变2-4 试分析图示体系的几何构造。
(a)几何不变(b)W=4×3 -3×2 -5=1>0几何可变体系(ⅠⅢ)(ⅡⅢ)几何不变(d)Ⅲ(ⅠⅢ)有一个多余约束的几何不变体(ⅠⅢ)(ⅡⅢ)(ⅠⅡ)舜变体系(f)(ⅠⅢ)(ⅡⅢ)无多余约束内部几何不变(h)二元体W=3×8 - 9×2 – 7= -1, 有1个多余约束2-5 试从两种不同的角度分析图示体系的几何构造。
(a)(ⅠⅢ)ⅠⅡⅢ(ⅠⅡ)(ⅡⅢ)舜变体系(b)Ⅲ(ⅡⅢ)(ⅠⅢ)同济大学朱慈勉 结构力学 第3章习题答案3-2 试作图示多跨静定梁的弯矩图和剪力图。
(a)2P F a 2P F a4P F Q34P F 2P F(b)aaaa a2m6m2m4m2m2020Q10/326/310(c)18060(d)3m2m2m3m3m4m3m2m2m2mA2m 2m2m2m7.5514482.524MQ3-3 试作图示刚架的内力图。
(a)242018616MQ18(b)4kN ·m 3m3m6m1k N /m2kN A CBD6m10kN3m3m 40kN ·mABC D30303011010QM 210(c)45MQ(d)3m3m 6m6m2m 2m444444/32MQN(e)4481``(f)4m4m2m3m4m222220M3-4 试找出下列各弯矩图形的错误之处,并加以改正。
(a)F P(b)(c)(d)(e)(f)F3-5 试按图示梁的BC 跨跨中截面的弯矩与截面B 和C 的弯矩绝对值都相等的条件,确定E 、F 两铰的位置。
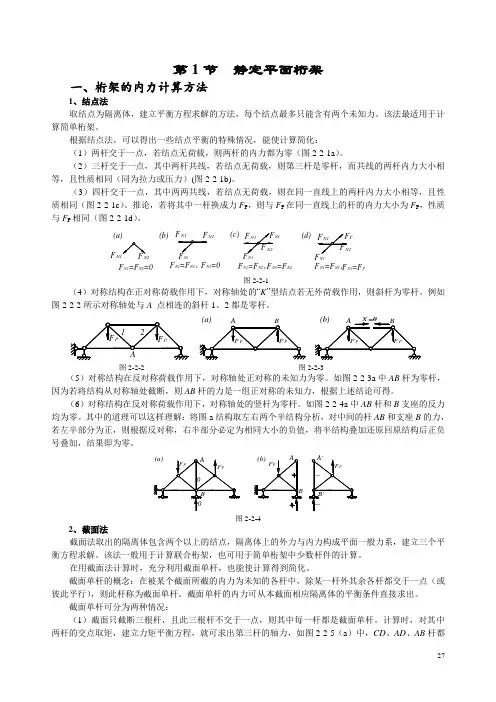
第1节 静定平面桁架一、桁架的内力计算方法1、结点法取结点为隔离体,建立平衡方程求解的方法,每个结点最多只能含有两个未知力。
该法最适用于计算简单桁架。
根据结点法,可以得出一些结点平衡的特殊情况,能使计算简化:(1)两杆交于一点,若结点无荷载,则两杆的内力都为零(图2-2-1a )。
(2)三杆交于一点,其中两杆共线,若结点无荷载,则第三杆是零杆,而共线的两杆内力大小相等,且性质相同(同为拉力或压力)(图2-2-1b)。
(3)四杆交于一点,其中两两共线,若结点无荷载,则在同一直线上的两杆内力大小相等,且性质相同(图2-2-1c )。
推论,若将其中一杆换成力F P ,则与F P 在同一直线上的杆的内力大小为F P ,性质与F P 相同(图2-2-1d )。
F N3F N3=0F N1=F N2=0F N3=F N4(a)(b)(c)F N4(d)F N3=F PF PN1F F N2F N1F N2F N1F N2F N1F N2F N3F N3F N1=F N2,F N1=F N2,F N1=F N2,图2-2-1(4)对称结构在正对称荷载作用下,对称轴处的“K ”型结点若无外荷载作用,则斜杆为零杆。
例如图2-2-2所示对称轴处与A 点相连的斜杆1、2都是零杆。
1A2F PF PAF PF PBF PF PBA(b)(a)X =0图2-2-2 图2-2-3(5)对称结构在反对称荷载作用下,对称轴处正对称的未知力为零。
如图2-2-3a 中AB 杆为零杆,因为若将结构从对称轴处截断,则AB 杆的力是一组正对称的未知力,根据上述结论可得。
(6)对称结构在反对称荷载作用下,对称轴处的竖杆为零杆。
如图2-2-4a 中AB 杆和B 支座的反力均为零。
其中的道理可以这样理解:将图a 结构取左右两个半结构分析,对中间的杆AB 和支座B 的力,若左半部分为正,则根据反对称,右半部分必定为相同大小的负值,将半结构叠加还原回原结构后正负号叠加,结果即为零。

考研结构力学考试题及答案# 考研结构力学考试题及答案## 一、选择题1. 在结构力学中,静定结构与超静定结构的区别是什么?- A. 静定结构的内力可以通过静力平衡条件确定- B. 超静定结构的内力需要通过变形协调条件确定- C. 静定结构的外力可以通过静力平衡条件确定- D. 超静定结构的外力需要通过变形协调条件确定答案:A2. 简支梁在均布荷载作用下的最大弯矩是多少?- A. \( \frac{qL}{2} \)- B. \( \frac{qL^2}{8} \)- C. \( \frac{qL^2}{4} \)- D. \( \frac{qL^3}{12} \)答案:C## 二、简答题1. 请简述平面桁架的几何不变性条件。
- 平面桁架的几何不变性条件是指,桁架在不发生结构变形的情况下,能够保持其几何形状不变的条件。
根据Maxwell-Betti定理,对于一个平面桁架,其几何不变性条件为:桁架的杆件数 \( m \) 必须大于等于节点数 \( n \) 减去1,即 \( m \geq n - 1 \)。
2. 什么是弯矩图?它在结构设计中有什么作用?- 弯矩图是表示梁或框架结构在不同截面上的弯矩分布情况的图形。
在结构设计中,弯矩图可以帮助工程师确定结构的最大弯矩值,从而合理选择材料和截面尺寸,确保结构的安全性和经济性。
## 三、计算题1. 已知一简支梁,跨度为 \( L \) 米,梁上作用有集中力 \( P \)位于梁中点。
求梁的最大弯矩。
- 根据弯矩的计算公式,对于简支梁在中点作用集中力的情况,最大弯矩 \( M_{max} \) 为:\[ M_{max} = \frac{PL}{4} \]2. 某平面桁架由三个节点和三个杆件组成,节点1和节点3固定不动,节点2可以自由移动。
请判断该桁架是否为几何不变体系,并说明理由。
- 根据几何不变性条件,对于平面桁架,杆件数 \( m \) 必须大于等于节点数 \( n \) 减去1。
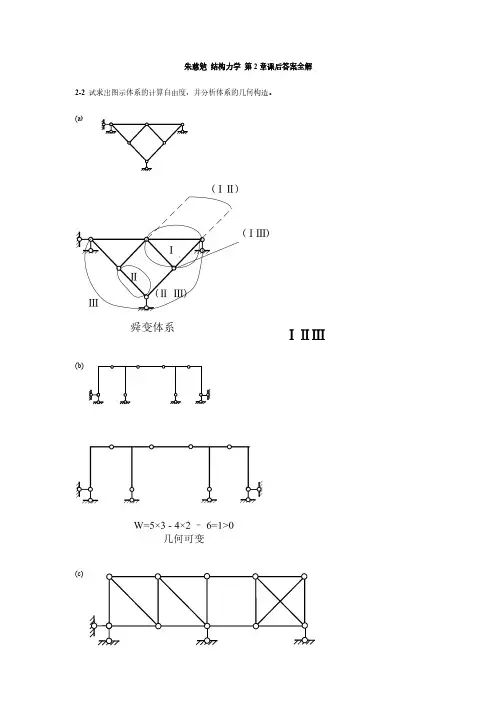
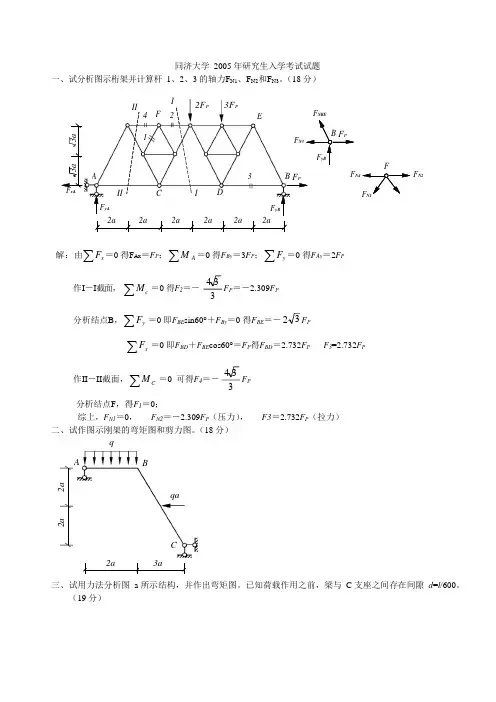
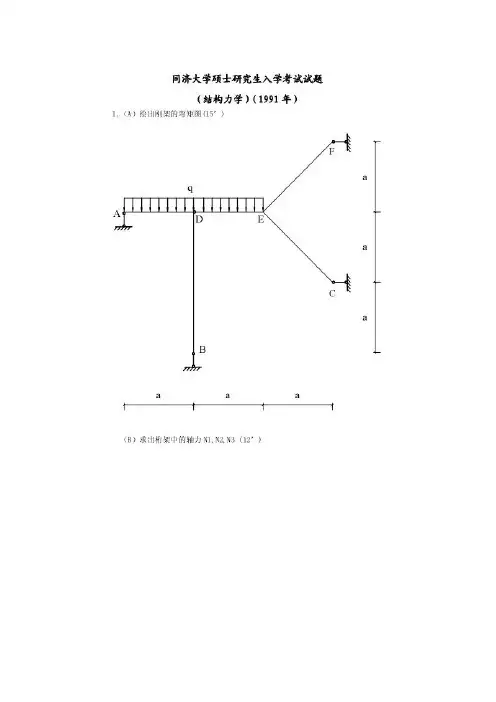
3 4 332a3a同济大学 2005 年研究生入学考试试题一、试分析图示桁架并计算杆 1、2、3 的轴力F N1、F N2和F N3。
(18 分)F NBEF F N4F N1F N2解:由∑ F x=0 得FAx =F P ;∑ MA =0 得F By =3F P ;∑ F y=0 得FAy =2F P作I -I 截面,∑ M c =0 得F 2=- F P =-2.309F P分析结点B ,∑ Fy =0 即F BE sin60°+F By =0 得F BE =- 2 F P∑ Fx =0 即F BD +F BE cos60°=F P 得F BD =2.732F P F 3=2.732F P作II -II 截面,∑M C =0 可得F 4=-F P 分析结点F ,得F 1=0;综上,F N1=0, F N2=-2.309F P (压力), F3=2.732F P (拉力)二、试作图示刚架的弯矩图和剪力图。
(18 分)q三、试用力法分析图 a 所示结构,并作出弯矩图。
已知荷载作用之前,梁与 C 支座之间存在间隙 d =l /600。
(19 分)2a2a2a2a2a 2aB F P F yBII4 F I2 2F P 3F PE1F N3A3B F PF xAII CI DF yAF yB4 33ABqaC2a 2a3a3a(b)F PM=F P ld ƒ (a)qAB(b)q3EICEIl l(c)(d)M 1图ql 2/2M P 图(e)(f)ql 2/16 -EI/400lM 图(1)解:取基本体系如图 b 所示。
列力法方程:δ11X 1+⊗1P =-dM 图(2)ql 2/8δ11= 1 3EI ⨯ l ⨯ l ⨯ l + 1 ⨯ 1 EI 2 ⨯ l ⨯ l ⨯ 2 ⨯ l =32l 33EI⊗1P =- 13EI ⨯ l ⨯ l ⨯9qlql 2 - 1 2 EI EI ⨯ 2 ⨯ l ⨯ 3 ql 2 2 ⨯ 5 ⨯ l = - 8 3ql 4 8EI 解方程得 X 1=16 -400l 2 ql 2ϒ( ) 9qlEI / ql 2 EI M A =M P + M 1 X 1 = 2 + ' - l ≤ ⨯ 16 - 400l 2 ∞ =- 16+ 400l 当M A >0 时,M 图如图e 所示;当M A <0 时,M 图如图f 所示。
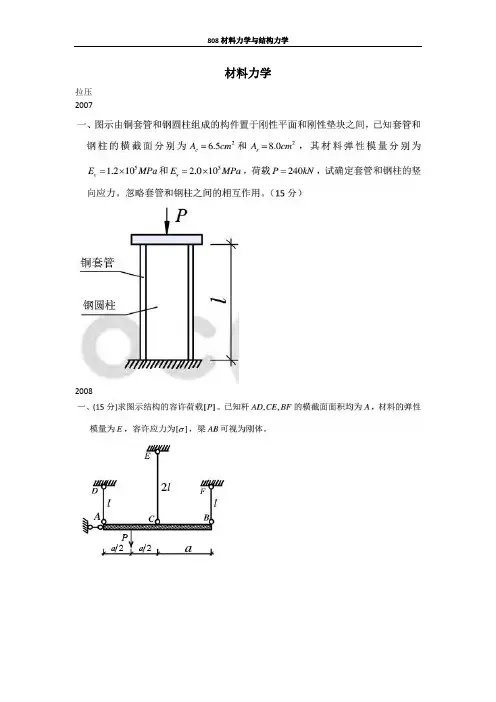
材料力学拉压2007200820102011二、如图所示杆系结构中,各杆EA均相同,许用拉应力均为[σ],试求:(1)、当A点处作用竖向力F P时,求F P的最大值;(2)、若已知AB杆哎制造时比原尺寸长∆,求各杆初始应力。
一、图示结构AB杆为实心圆杆,其截面抗扭刚度为GI P;CD杆为刚性杆,竖杆CF、DH位于与平面yAz平行的同一平面内,其截面轴向刚度为EA。
已知绕x轴的力矩Mx作用在B 结点处,试求CF、DH杆的轴力以及AB杆所受的扭矩。
扭转20072008200920102011平面弯曲、应力状态、强度理论、组合变形200720082009四、图示工字钢制成的简支梁,腹板位于竖直平面内,截面高度为25cm,翼缘宽度和厚度各为11.8cm和 1.3cm,腹板厚度为1cm。
材料的容许正应力[σ]=160MPa,容许剪应力[τ]=100MPa,试用第三强度理论对该梁进行强度校核。
五、截面半径为R的圆直杆AB和BC在水平面内,A端固定,AB与BC刚接且相互垂直,弹性模量为E,泊松比为ν。
通过C截面形心,垂直于BC杆张拉一根拉锁CD,CD与y方向成θ角。
测得H截面g点处沿x正方向的线应变为ε0。
试求:(1)拉索的张力N CD;(2)H截面h 点处,在杆件表面上与x正方向和y正方向均成45°角的线应变ε45°。
2010二、根据弯矩、剪力、荷载间的关系作出图示多跨静定梁的剪力图和弯矩图。
四、如图所示,悬臂梁截面为矩形b×h=90×180,承受荷载,,悬臂梁材料的弹性模量E=10GPa,试求:(1)梁内最大x向正应力及其作用点位置;(2)梁的最大转角;(3)梁矩形截面的截面核心。
五、弹性体内某点的应力状态为平面应力状态,如图所示,,,,材料的弹性模量为E=210GPa,泊松比为v=0.3。
(1)试用解析法求该点的主应力,并画出主应力单元体;(2)求该点的最大剪应力;(3)求该点的主应变。
朱慈勉 结构力学 第2章课后答案全解2-2 试求出图示体系的计算自由度,并分析体系的几何构造。
(a )ⅠⅡⅢ(ⅠⅡ)(ⅠⅢ)(Ⅱ Ⅲ)舜变体系`ⅠⅡⅢ(b)W=5×3 - 4×2 – 6=1>0几何可变(c)有一个多余约束的几何不变体系(d)2-3 试分析图示体系的几何构造。
(a)(ⅠⅢ)ⅠⅡⅢ(ⅠⅡ)(Ⅱ Ⅲ)几何不变W=3×3 - 2×2 – 4=1>0可变体系ⅠⅡⅢ(ⅠⅡ)(ⅠⅢ)(ⅡⅢ)几何不变2-4 试分析图示体系的几何构造。
(a)(ⅠⅢ)(ⅠⅡ)(ⅡⅢ)ⅠⅡⅢ几何不变(b)W=4×3 -3×2 -5=1>0几何可变体系ⅢⅠⅡ(ⅠⅢ)(ⅡⅢ)(ⅠⅡ)几何不变(d)(ⅠⅡ)ⅢⅠⅡ(ⅡⅢ)(ⅠⅢ)二元杆有一个多余约束的几何不变体ⅠⅡⅢ(ⅠⅢ)(ⅡⅢ)(ⅠⅡ)舜变体系(f)ⅠⅡⅢ(ⅠⅢ)(ⅡⅢ)(ⅠⅡ)无多余约束内部几何不变ⅠⅡⅢ(ⅠⅢ)(ⅠⅡ)(ⅡⅢ)二元体(h)ⅠⅡⅢ(ⅠⅢ)(ⅠⅡ)(ⅡⅢ)二元体多余约束W=3×8 - 9×2 – 7= -1, 有1个多余约束2-5 试从两种不同的角度分析图示体系的几何构造。
(a)(ⅠⅢ)ⅠⅡⅢ(ⅠⅡ)(ⅡⅢ)舜变体系(b)ⅠⅡⅢ(ⅠⅡ)(ⅡⅢ)(ⅠⅢ)几何不变同济大学朱慈勉 结构力学 第3章习题答案3-2 试作图示多跨静定梁的弯矩图和剪力图。
(a)4P F a2P F a 2P F a M4P F Q34P F 2P F(b)ABCaa aaaF P a DEFF P2m6m2m4m2mABCD10kN2kN/m42020M Q10/326/3410(c)21018018040M1560704040Q(d)3m2m2mA B CEF15kN 3m3m4m20kN/mD 3m2m2m2mA2m 2m2mABCD E FG H 6kN ·m4kN ·m 4kN2m7.5514482.524MQ3-3 试作图示刚架的内力图。

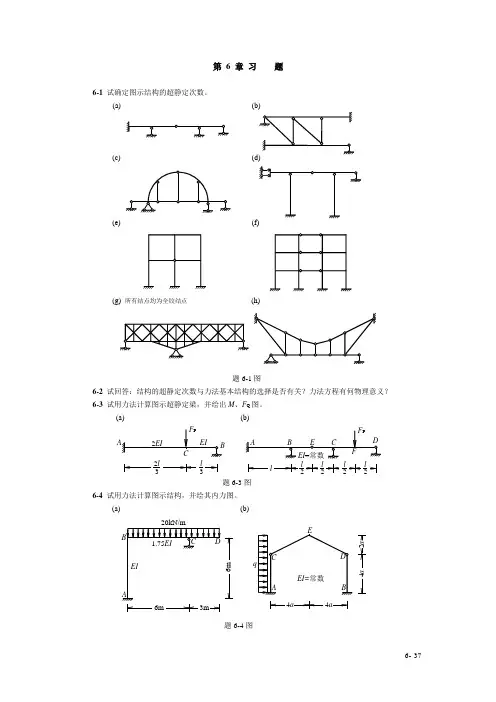
6- 37第 6 章 习 题6-1 试确定图示结构的超静定次数。
(a) (b)(c)(e)(g) 所有结点均为全铰结点(h)题6-1图6-2 试回答:结构的超静定次数与力法基本结构的选择是否有关?力法方程有何物理意义? 6-3 试用力法计算图示超静定梁,并绘出M 、F Q 图。
(a) (b)题6-3图6-4 试用力法计算图示结构,并绘其内力图。
(a)(b)题6-4图4a 2a4a4a3m6m6m2l 3l 3l2l 2 l2ll 26- 386-5 试用力法计算图示结构,并绘出M 图。
(b) (c) (d)题6-5图6-6 试用力法求解图示超静定桁架,并计算1、2杆的内力。
设各杆的EA 均相同。
(a)(b)题6-6图6-7 试用力法计算图示组合结构,求出链杆轴力并绘出M 图。
(a) (b)题6-7图6-8 试利用对称性计算图示结构,并绘出M 图。
6m6m3m3m6m6maaa1.5m6m3m6m3ml la aaa6- 39(a) (b) (c) (d)(e) (f)( BEH 杆弯曲刚度为2EI ,其余各杆为EI )(g) (h)题6-8图6-9 试回答:用力法求解超静定结构时应如何恰当地选取基本结构? 6-10 试绘出图示结构因支座移动产生的弯矩图。
设各杆EI 相同。
(a)hll ll3m4m5m4m60kNA BC DEI=常数llAB CDEI=常数qqlllDEAB EI=常数qqC Faaa2a 2aaaaaa6m 6m 9m2l2l 2 l l6- 40(b)题6-10图6-11 试绘出图示结构因温度变化产生的M 图。
已知各杆截面为矩形,EI=常数,截面高度h=l/10,材料线膨胀系数为α。
(a) (b)题6-11图6-12 图示平面链杆系各杆l 及EA 均相同,杆AB 的制作长度短了 ,现将其拉伸(在弹性范围内)拼装就位,试求该杆轴力和长度。
题6-12图 题6-13图6-13 刚架各杆正交于结点,荷载垂直于结构平面,各杆为相同圆形截面,G = 0.4 E ,试作弯矩图和扭矩图。
朱慈勉结构力学第2章课后答案全解2-2试求出图示体系的计算自由度,并分析体系的几何构造。
(a)(ⅠⅡ)(ⅠⅢ)Ⅰ`Ⅱ(ⅡⅢ)Ⅲ舜变体系ⅠⅡⅢ(b)W=5×3-4×2–6=1>0几何可变(c)有一个多余约束的几何不变体系(d)W=3×3-2×2–4=1>0可变体系2-3试分析图示体系的几何构造。
(a)(ⅠⅢ)ⅠⅢ几何不变(ⅠⅡ)Ⅱ(ⅡⅢ)(ⅡⅢ)(ⅠⅡ)ⅠⅡ(ⅠⅢ)Ⅲ几何不变2-4试分析图示体系的几何构造。
(a)ⅠⅡ(ⅡⅢ)(ⅠⅡ)(ⅠⅢ)Ⅲ几何不变(b)W=4×3-3×2-5=1>0几何可变体系(ⅠⅢ)(ⅡⅢ)Ⅰ(ⅠⅡ)ⅡⅢ几何不变(d)二元杆ⅡⅠ(ⅠⅡ)Ⅲ(ⅡⅢ)(ⅠⅢ)有一个多余约束的几何不变体ⅢⅠⅡ(ⅡⅢ)(ⅠⅢ)(ⅠⅡ)舜变体系(f)Ⅲ(ⅠⅢ)(ⅡⅢ)ⅠⅡ(ⅠⅡ)无多余约束内部几何不变(ⅠⅢ)(ⅠⅡ)二元体(ⅡⅢ)ⅠⅡⅢ(h)(ⅡⅢ)(ⅠⅢ)Ⅱ多余约束Ⅰ(ⅠⅡ)ⅢW=3×8-9×2–7=-1,有1个多余约束二元体2-5试从两种不同的角度分析图示体系的几何构造。
(a)ⅡⅠ(ⅠⅡ)Ⅲ(ⅠⅢ)舜变体系(ⅡⅢ)(b)(ⅡⅢ)几何不变ⅡⅠ(ⅠⅡ)Ⅲ(ⅠⅢ)同济大学朱慈勉结构力学第3章习题答案3-2试作图示多跨静定梁的弯矩图和剪力图。
(a)FP F P aA B CD E Fa a a a aMF aP2F aP2F aP4QFP4FP23FP4(b)2kN/m10kNA B C D2m6m2m4m2mM结构力学答案-同济大学朱慈勉2020Q (c)410/310426/315kN20kN/mA B C D E F2m2m3m3m3m4m180M4018070210Q4015(d)606kN·m4kN·m404kNA B C D E F G H3m2m2m2m2m2m2m2m1/ 结构力学答案-同济大学朱慈勉M7.5148Q 5442.523-3 试作图示刚架的内力图。