实验一 典型连续时间信号描述及运算

实验一连续时间信号的Matlab表示与计算一、实验目的1、初步学习MATLAB语言，熟悉MATLAB软件的基本使用。

2、掌握用MA TLAB描述连续时间信号方法，能够编写MATLAB程序，实现各种信号的时域变换和运算，并且以图形的方式再现各种信号的波形。

二、实验原理连续信号是指自变量的取值范围是连续的，且对于一切自变量的取值，除了有若干个不连续点之外，信号都有确定的值与之对应。

严格来说，MATLAB并不能处理连续信号，而是用等时间间隔点的样值来近似表示连续信号。

当取样时间间隔足够小时，这些离散的样值就能较好地近似连续信号。

在MATLAB可视化绘图中，对于以t为自变量的连续信号，在绘图时统一用plot函数；而对n为自变量的离散序列，在绘图时统一用stem函数。

对于连续时间信号f（t），可用f、t两个行向量来表示。

例：t=-10：1.5：10；f=sin(t)./ t ;可以产生t= -10~10，间隔1.5的序列以及t tf)sin(=的值。

用命令：plot(t,f)可得如下图形，显然显示效果较差，这是因为t的间隔过大，只要改变为：t=-10：0.5：10；可得图1.2。

图1.1 图1.21. 信号的时域表示方法MATLAB提供了大量用以生成基本信号的函数，比如最常用的指数信号、正弦信号等就是MATLAB的内部函数，即不需要安装任何工具箱就可以调用的函数。

1.1单位阶跃信号u(t)function y=heaviside(t) %阶跃信号y = (t>=0); % y = 1 for t > 0, else y = 01.2单位冲激信号δ(t)function chongji(t1,t2,t0) %冲激信号δ(t- t 0)，t 1和t 2分为起始时间和终止时间dt=0.01;t=t1:dt:t2;n=length(t);x=zeros(1,n);x(1,(t0-t1)/dt+1)=1/dt;stairs(t,x); %以阶梯方式绘画axis([t1,t2,0,1.1/dt]) 或function y = delta(t)dt = 0.01;y = (u(t)-u(t-dt))/dt;1.3指数信号指数信号atAe 在MATLAB 中可以用exp 函数表示，其调用形式为：y=A*exp(a*t)例如图1-3所示指数衰减信号的MATLAB 源程序如下（取A=1，a=-0.4）：%program7_1 Decaying expponential signalA=1;a=-0.4;t=0:0.01:10;ft=A*exp(a*t);plot(t,ft);grid on;1.4正弦信号正弦信号)cos(ϕω+t A o 和)sin(ϕω+t A o 分别用MATLAB 的内部函数cos 和sin 表示，其调用形式为：)*cos(*phi t A o +ω)*sin(*phi t A o +ω 例如图1-4所示MATLAB 源程序如下（取A=1，πω20=，6/πϕ=）：%program7_2 Sinusoidal signalA=1;w0=2*pi;phi=pi/6;t=0:0.01:8;ft=A*sin(w0*t+phi);plot(t,ft);grid on;图1-3 单边指数衰减信号 图1-4 正弦信号 除了内部函数外，在信号处理工具箱（Signal Processing Toolbox ）中还提供了诸如抽样 函数、矩形波、三角波、周期性矩形波和周期性三角波等在信号处理中常用的信号。

实验1 信号的时域描述与运算一、实验目的1. 掌握信号的MATLAB 表示及其可视化方法。

2. 掌握信号基本时域运算的MATLAB 实现方法。

3. 利用MATLAB 分析常用信号，加深对信号时域特性的理解。

二、实验原理与方法1. 连续时间信号的MATLAB 表示连续时间信号指的是在连续时间范围内有定义的信号，即除了若干个不连续点外，在任何时刻信号都有定义。

在MATLAB 中连续时间信号可以用两种方法来表示，即向量表示法和符号对象表示法。

从严格意义上来说，MATLAB 并不能处理连续时间信号，在MATLAB 中连续时间信号是用等时间间隔采样后的采样值来近似表示的，当采样间隔足够小时，这些采样值就可以很好地近似表示出连续时间信号，这种表示方法称为向量表示法。

表示一个连续时间信号需要使用两个向量，其中一个向量用于表示信号的时间范围，另一个向量表示连续时间信号在该时间范围内的采样值。

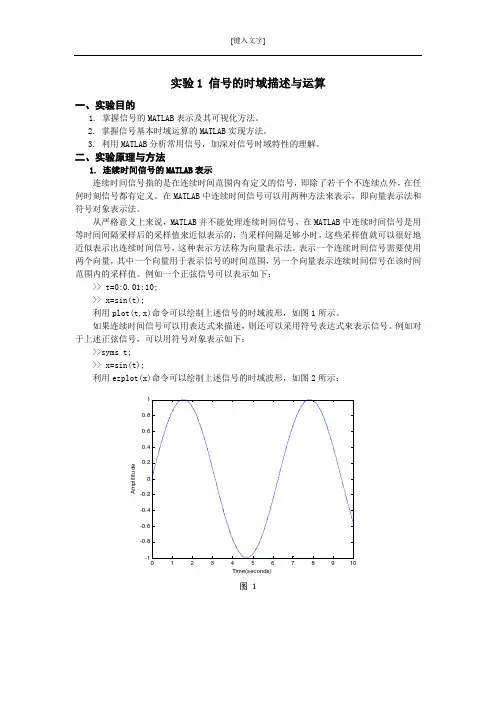
例如一个正弦信号可以表示如下：>> t=0:0.01:10; >> x=sin(t);利用plot(t,x)命令可以绘制上述信号的时域波形，如图1所示。

如果连续时间信号可以用表达式来描述，则还可以采用符号表达式來表示信号。

例如对于上述正弦信号，可以用符号对象表示如下：>>syms t; >> x=sin(t);利用ezplot(x)命令可以绘制上述信号的时域波形，如图2所示：图 1Time(seconds)A m p l i t i t u d e图表 2matlab 提供了一些函数用于常用信号的产生，例如阶跃信号、脉冲信号、指数信号、正弦信号等，表中列出了一些常用的基本函数。

常用的信号产生函数2.连续时间信号的时域运算对连续时间信号的运算包括两信号相加、相乘、微分、积分，以及位移、反转、尺度变换（尺度伸缩）等。

1）相加和相乘信号相加和相乘指两信号对应时刻的值相加和相乘，对于两个采用向量表示的可以直接使用算术运算的运算符“+”和“*”来计算，此时要求表示两信号的向量时间范围和采样间隔相同。

实验一连续时间信号的时域和频域分析一. 实验目的：1. 熟悉MATLAB 软件平台。

2. 掌握MATLAB 编程方法、常用语句和可视化绘图技术。

3. 编程实现常用信号及其运算MATLAB 实现方法。

4. 编程实现常用信号的频域分析。

二. 实验原理：1、连续时间信号的描述：（1）向量表示法连续信号是指自变量的取值范围是连续的，且对于一切自变量的取值，除了有若干个不连续点之外，信号都有确定的值与之对应。

严格来说，MATLAB 并不能处理连续信号，而是用等时间间隔点的样值来近似表示连续信号。

当取样时间间隔足够小时，这些离散的样值就能较好地近似连续信号。

矩阵是MATLAB 进行数据处理的基本单元，矩阵运算是MATLAB 最重要的运算。

通常意义上的数量（也称为标量）在MATLAB 系统中是作为1×1 的矩阵来处理的，而向量实际上是仅有一行或者一列的矩阵。

通常用向量表示信号的时间取值范围，如t = -5:5，但信号x(t)、向量t 本身的下标都是从1 开始的，因此必须用一个与向量x 等长的定位时间变量t，以及向量x，才能完整地表示序列x(t)。

在MATLAB 可视化绘图中，对于以t 为自变量的连续信号，在绘图时统一用plot 函数；而对n 为自变量的离散序列，在绘图时统一用stem 函数。

（2）符号运算表示法符号对象(Symbolic Objects 不同于普通的数值计算)是Matlab 中的一种特殊数据类型，它可以用来表示符号变量、表达式以及矩阵，利用符号对象能够在不考虑符号所对应的具体数值的情况下能够进行代数分析和符号计算(symbolic math operations)，例如解代数方程、微分方程、进行矩阵运算等。

符号对象需要通过sym 或syms 函数来指定, 普通的数字转换成符号类型后也可以被作为符号对象来处理.我们可以用一个简单的例子来表明数值计算和符号计算的区别: 2/5+1/3 的结果为0.7333(double 类型数值运算), 而sym(2)/sym(5)+sym(1)/sym(3)的结果为11/15, 且这里11/15 仍然是属于sym 类型, 是符号数。

实验一 连续时间信号的采样一、实验目的进一步加深对采样定理和连续信号傅立叶变换的理解。

实验步骤1．复习采样定理和采样信号的频谱采样定理如果采样频率s F 大于有限带宽信号)(t x a 带宽0F 的两倍，即02F F s > （1）则该信号可以由它的采样值)()(s a nT x n x =重构。

否则就会在)(n x 中产生混叠。

该有限带宽模拟信号的02F 被称为乃魁斯特频率。

必须注意，在)(t x a 被采样以后，)(n x 表示的最高模拟频率为2/s F Hz （或πω=）。

2．熟悉如何用MATLAB 语言实现模拟信号表示严格地说，除了用符号处理工具箱(Symbolics)外，不可能用MATLAB 来分析模拟信号。

然而如果用时间增量足够小的很密的网格对()a x t 采样，就可得到一根平滑的曲线和足够长的最大时间来显示所有的模态。

这样就可以进行近似分析。

令t ∆是栅网的间隔且s t T ∆<<，则()()G a x m x m t ∆=∆ （2）可以用一个数组来仿真一个模拟信号。

不要混淆采样周期s T 和栅网间隔t ∆，因为后者是MATLAB 中严格地用来表示模拟信号的。

类似地，付利叶变换关系也可根据（2）近似为：∑∑∆Ω-∆Ω-∆=∆≈Ωmt m j G m t m j G a e m x t t em x j X )()()( （3） 现在，如果)(t x a （也就是)(m x G ）是有限长度的。

则公式（3）与离散付利叶变换关系相似，因而可以用同样的方式以MATLAB 来实现，以便分析采样现象。

3．根据提供的例子程序，按照要求编写实验用程序；三、实验内容（1）通过例一熟悉用MATLAB 语言实现描绘连续信号的频谱的过程，并在MATLAB 语言环境中验证例1的结果；例1、令t a et x 1000)(-=，求出并绘制其付利叶变换。

解：根据傅立叶变换公式有010*********.002()()1()1000j t t j t t j t a a X j x t e dt e e dt e e dt ∞∞-Ω-Ω--Ω-∞-∞Ω==+=Ω+⎰⎰⎰ （4） 因为)(t x a 是一个实偶信号，所以它是一个实值函数。

实验一 典型连续时间信号和离散时间信号一、实验目的掌握利用Matlab 画图函数和符号函数显示典型连续时间信号波形、典型时间离散信号、连续时间信号在时域中的自变量变换。

二、实验内容1、典型连续信号的波形表示（单边指数信号、复指数信号、抽样信号、单位阶跃信号、单位冲击信号）a. 画出教材P28习题1-1(3) ()[(63)(63)]t f t e u t u t =----的波形图。

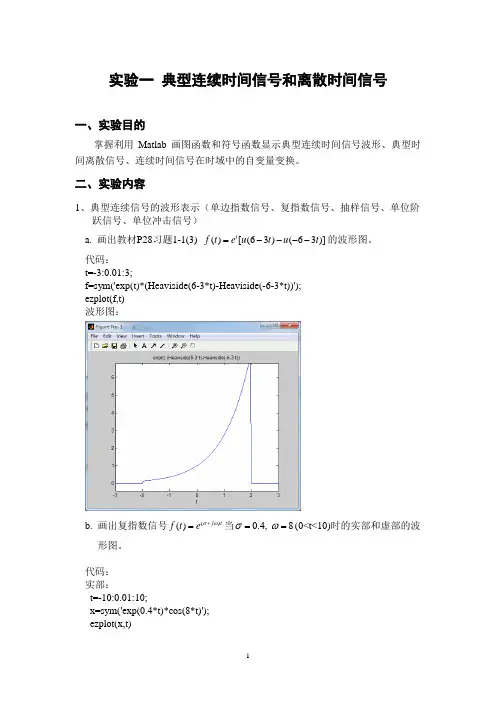
代码：t=-3:0.01:3;f=sym('exp(t)*(Heaviside(6-3*t)-Heaviside(-6-3*t))');ezplot(f,t)波形图：b. 画出复指数信号()()j t f t e σω+=当0.4, 8σω==(0<t<10)时的实部和虚部的波形图。

代码：实部：t=-10:0.01:10;x=sym('exp(0.4*t)*cos(8*t)');ezplot(x,t)波形图：虚部：t=-10:0.01:10;x=sym('exp(0.4*t)*sin(8*t)');ezplot(x,t)c. 画出教材P16图1-18，即抽样信号Sa(t)的波形。

代码：f=sym('sin(t)/t');t=-10:0.01:10;ezplot(f,t)d. 用符号函数sign画出单位阶跃信号u(t-3)的波形（0<t<10）。

t=0:0.01:10;y=(sgn(t-3)+1)/2;plot(t,y)e. 单位冲击信号可看作是宽度为∆，幅度为1/∆的矩形脉冲，即t=t1处的冲击信号为11111 ()()0 t t t x t t t otherδ∆⎧<<+∆⎪=-=∆⎨⎪⎩画出0.2∆=,t 1=1的单位冲击信号。

t=0:0.01:2;f=sym('5*(Heaviside(t-1)-Heaviside(t-1.2))');ezplot(f,t)2、典型离散信号的表示（单位样值序列、单位阶跃序列、实指数序列、正弦序列、复指数序列）编写函数或程序来产生下列基本脉冲序列：a. 单位脉冲序列，起点n 0，终点n f ，在n s 处有一单位脉冲。

姓名： 周强 班级： 电信1004班 学号： 201004135136实验1 时域连续信号的表示及运算一、 实验目的1．掌握常用时域连续信号的MA TLAB 表示方法。

2．掌握连续信号的基本运算，包括信号相加与相乘、微分与积分、平移、反转、尺度变换、奇偶分解、卷积积分等。

二、 实验原理及方法MATLAB 利用连续信号在等时间间隔点的采样值来近似表示连续信号。

三、 实验内容及步骤1. 利用MATLAB 命令画出下列连续信号的波形图。

（1）)()2(t u e t--源代码 （1 ） )()2(t u e t -- 图像 t=0:0.001:8;y=(2-exp(-t)).*heaviside(t);plot(t,y);grid onaxis([0 8 1 2])波形图（2）)(cos t u源代码：t=0:0.01:2*pi;y=heaviside(cos(t));plot(t,y);grid onaxis([0 2*pi 0 1])波形图（3）产生幅度为1、周期为1、占空比为0.5的周期矩形信号。

源代码t=0:0.01:8; 波形图y=heaviside(sin(2*pi*t));plot(t,y);grid onaxis([0 4 0 1.2]);2. 已知)(t f 的波形如图1-15所示，做出)()(t f t f +、)()(t f t f ⋅、)(t f 的微分、)(t f 的积分、)43(t f -的波形。

)(t f 的图像代码syms t yy=t*(heaviside(t)-heaviside(t-1))+heaviside(t-2)-heaviside(t-1);ezplot(t ,y);grid onaxis([0 4 -1.5 1.5]))(t f 的图像t )(t f 01121-图1-15)()(t f t f +源代码syms t y y1y1=t*(heaviside(t)-heaviside(t-1))+heaviside(t-2)-heaviside(t-1);y=y1+y1; )()(t f t f +波形图ezplot(t,y);grid onaxis([0 4 -2.1 2.1]))()(t f t f ⋅源代码syms t yy=t*(heaviside(t)-heaviside(t-1))+heaviside(t-2)-heaviside(t-1);ezplot(t ,y*y);grid onaxis([0 4 -2.1 2.1])波形图)(t f 的微分syms t y fy=t*(heaviside(t)-heaviside(t-1))+heaviside(t-2)-heaviside(t-1);f=diff(y,'t');t=0:0.01:4; )(tf的微分波形图ezplot(f,t);grid onf的积分)(t源代码syms t y f y1y=t*(heaviside(t)-heaviside(t-1))+heaviside(t-2)-heaviside(t-1);f=int(y,'t');t=0:0.01:4;ezplot(f,t);grid on波形图3(tf4)源代码syms t y1 yy1=t*(heaviside(t)-heaviside(t-1))+heaviside(t-2)-heaviside(t-1);y=subs(y1,t,3-4*t);ezplot(t ,y);grid onaxis([0 1.2 -1.2 1.2])波形图实验心得与小结：（1）学会了单位阶跃函数heaviside()的使用，掌握了用matlab画一些连续信号的波形图（2）掌握了对一些基本的函数求微分，积分，翻转，平移的方法，还有一些符号变量的使用（3）学会了如何利用三角函数的周期性画出周期性的单位阶跃函数体会：在学习的过程中只有不断的尝试，才能从其中学到一些东西，在上机的过程中，我们不能只会画几个图像就以为学会了，从理解到自己能熟练运用还有一段距离，只有不断的从实验中发现错误才能提高自己，才能有收获。

实验一 连续时间信号1．对下面信号创建符号表达式 ()()t T t t x ππ2cos 2sin )(=对于T=4，8和16，利用ezplot 画出320≤≤t 内的信号。

什么是)(t x 的基波周期？实验思路：建立符号函数，再用函数subs 替换T 的值，得到相应的t 的表达式，在用ezplot 画出图形，在画出网格，得出基波周期。

实验内容；实验代码：x=sym('(sin(2*pi*t/T)*(cos(2*pi*t/T)))') x4=subs(x,'T',4) x8=subs(x,'T',8);x16=subs(x,'T',16);subplot(3,1,1);ezplot(x4,[0 32]); subplot(3,1,2);ezplot(x8,[0 32]); subplot(3,1,3);ezplot(x16,[0 32])实验结果：实验结果分析：x4的基波周期有图可以看出，后面两个x8\x16的是2．对下面信号创建一个符号表达式()t e t x at π2cos )(-=对于81,41,21=a ，利用ezplot 确定d t ，d t 为)(t x 最后跨过0.1的时间，将d t 定义为该信号的消失的时间。

利用ezplot 对每一个a 值确定在该信号消失之前，有多少个完整的余弦周期出现，周期数目是否正比于品质因素aT Q 2)2(π=？ 实验思路：建立符号函数()t e t x at π2cos )(-=，再用函数subs 替换a 的值，得到相应的关于t 的表达式x1\x2\x3，在用ezplot 画出图形，再画出网格，找出跨过0.1的坐标点，得出td,及信号消失的时间，数出周期数，和品质因素相比较即可。

实验内容x=sym('exp(-a*t)*cos(2*pi*t)') x1=subs(x,'a',1/2);x2=subs(x,'a',1/4); x3=subs(x,'a',1/8);subplot(3,1,1);ezplot(x1,[0 10]);grid; subplot(3,1,2);ezplot(x2,[0 20]);grid; subplot(3,1,3);ezplot(x3,[0 40]);grid 实验结果另外两个坐标是信号消失前有的余弦波个数为，4、8、16、与品质因素成正比3．将信号82162)(t j t j e e t x ππ+=的符号表达式存入x 中4．写出函数)(x sreal xr =，它产生一个代表)(t x 实部的符号表达式xr 。

典型连续时间信号描述及运算理论基础1.向量表示方法对于连续时间信号 f (t) ，可以定义两个行向量 f 和t 来表示，其中向量t 是形如t t1: p : t2的MATLAB 命令定义的时间范围向量，t1为信号起始时间，t2为终止时间，p 为时间间隔。

向量f 为连续时间信号f (t) 在向量t 所定义的时间点上的样值。

2.符号运算表示法如果信号可以用一个符号表达式来表示，则可用ezplot 命令绘制出信号的波形。

问题一：三种典型信号的绘制正弦信号E=150; T1=100; T2=200; o1=0; o2=pi/5;% 正弦表达式中的常数t=-200:250;f1=E.*sin((2.*pi.*t)/T1+o1);f2=E.*sin((2.*pi.*t)/T2+o1);f3=E.*sin((2.*pi.*t)/T2+o2);figure(1);plot(t,f1);title("正弦信号一");figure(2);plot(t,f2);title("正弦信号二");figure(3);plot(t,f3);title("正弦信号三");1212% 衰减信号E=200; T=100; tao=250;t=0:500;f=E.*sin((2.*pi.*t)/T).*exp(t./tao).*heaviside(t);plot(t,f);title("衰减函数");% 钟型信号E=400; tao1=100; tao2=150; tao3=200;t=-250:250;f1=E.*exp(-1.*(t.*t)./(tao1.*tao1));f2=E.*exp(-1.*(t.*t)./(tao2.*tao2));f3=E.*exp(-1.*(t.*t)./(tao3.*tao3));figure(1);plot(t,f1);title("钟型信号一");figure(2);plot(t,f2);title("钟型信号二");figure(3);plot(t,f3);title("钟型信号三");问题二：书上习题绘制syms tf1=str2sym('t.*heaviside(t)');figure(1);fplot(f1);title("第一小题");f2=str2sym('t.*heaviside(t-1)');figure(2);fplot(f2);title("第三小题");f3=str2sym('(2-exp(-t)).*heaviside(t-1)');figure(3);fplot(f3);title("第五小题");f8=str2sym('exp(-t).*cos(10.*pi.*t).*(heaviside(t-1)-heaviside(t-2))'); figure(4);fplot(f8);title("第八小题");问题三：三种奇异信号的绘制符号函数t=-5:0.01:5;f=sign(t);plot(t,f);title("符号函数")% 阶跃信号t=-5:0.01:5;f=1/2+1/2*sign(t);plot(t,f);title("阶跃信号")% 单位冲激函数chongji(-1,5,0);function chongji(t1,t2,t0)dt=0.01;t=t1:dt:t2;n=length(t);x=zeros(1,n);x(1,(-t0-t1)/dt+1)=1/dt;stairs(t,x);axis([t1,t2,0,1.2/dt])title('单位冲激信号δ (t) ')问题四：信号的运算%第一题syms tf1=str2sym('(-t+4)*(heaviside(t)-heaviside(t-4))'); y1=subs(f1,t,-t);f3=f1+y1;fplot(f3);%第三题syms tf1=str2sym('(-t+4)*(heaviside(t)-heaviside(t-4))'); y1=subs(f1,t,-t);f3=f1+y1;f2=str2sym('sin(2*pi*t)');f5=f3.*f2;fplot(f5);% 第五题syms tf1=str2sym('(-t+4)*(heaviside(t)-heaviside(t-4))'); f2=str2sym('sin(2*pi*t)');f6=f1.*f2;y=subs(f6,t,t-2);f7=y+f2;fplot(f7);问题五：直交流分量t=1:0.1:500;f=100*abs(sin(2.*pi.*t./50));fd=mean(f);fD=ones(1,length(t)).*fd;fA=f-fD;plot(t,f,t,fD,t,fA);title("直交流分量");遇到的问题和解决方法用matlab子程序实现阶跃函数u(t)的时候出现错误，我认为是数据类型不符，后来把u(t)用内置阶跃函数heaviside(t)代替就能够正常运行了。

连续时间信号的常用运算[例1]在时间]1,0[∈t 内生成幅度按指数衰减的正弦信号at e t A t x -+=)sin()(0φω=t e 6)8sin(5-π。

A=5;f0=4;phi=0;w0=2*pi*f0;a=6;t=0:0.001:1;x=A*sin(w0*t+phi).*exp(-a*t);%注意这里是点乘plot(t,x);ylabel('x(t)');xlabel('Time(s)');[例2]已知信号f(t)的波形，画出()()()()2332----t f t f t f t f ，，，的波形图。

clear all ;close all ;clct=-5:0.01:5;y1=2*exp(-(t/4).^2);y2=2*exp(-((t-2)/4).^2);y3=2*exp(-(3*t/4).^2);y4=2*exp(-(-t/4).^2);subplot(2,2,1);plot(t,y1);axis([-6,6,0,3]);title('f1(t)');grid on ;subplot(2,2,2);plot(t,y2);axis([-6,6,0,3]);title('f2(t)');grid on ;subplot(2,2,3);plot(t,y3);axis([-6,6,0,3]);title('f3(t)');grid on ;subplot(2,2,4);plot(t,y4);axis([-6,6,0,3]);title('f4(t)');grid on ;-5050123f1(t)-505123f2(t)-5050123f3(t)-505123f4(t)[例3]已知()()()t t f t t f Ω=Ω=8sin ,sin 21，使用命令画出两信号和及两信号乘积的波形图。

《信号与系统》实验报告姓名：学号：同组人：无指导教师：成绩：实验一典型连续时间信号描述及运算实验报告要求：（1）仿照单边指数信号的示例程序，按要求完成三种典型连续信号，即：正弦信号、衰减正弦信号、钟型信号的波形绘制。

（要求：要附上程序代码，以下均如此，不再说明）（2）根据《信号与系统》教材第一章的习题1.1（1，3，5，8）函数形式绘制波形。

（3）完成三种奇异信号，即：符号函数、阶跃信号、单位冲激信号的波形绘制。

（4）完成实验一中信号的运算：三、6 实验内容中的（1）（2）（3）（4）。

（5）求解信号的直流/交流分量，按第四部分的要求完成。

正文：（1）<1>正弦信号：代码：>> t=-250:1:250;>> f1=150*sin(2*pi*t/100);>> f2=150*sin(2*pi*t/200);>> f3=150*sin(2*pi*t/200+pi/5);>> plot(t,f1,'-',t,f2,'--',t,f3,'-.')<2>衰减正弦信号<3>代码：>> t=-250:1:250;>> f1=400*exp(-1.*t.*t./10000);>> f1=400*exp(-1.*t.*t./22500);>> f1=400*exp(-1.*t.*t./62500);>> plot(t,f1,'-',t,f2,'--',t,f3,'-.') (2)习题1，3，5，8<1>代码：t=0:1:10;f=t;plot(t,f)<3>代码：t=1:1:10;f=t;plot(t,f)<5>代码：t=0:1:10;f=2-exp(-1.*t.);plot(t,f)<8>代码：t=1:0.1:2;f=exp(-1.*t.)*cos(10*pi*t);plot(t,f)(3)三种奇异函数<1>符号函数代码: t=-5:0.05:5;f=sign(t);plot(t,f)<2>阶跃信号代码:>> t=-5:0.1:5;>> f=u(t);>> plot(t,f)<3>单位冲激信号代码：function chongji(t1,t2,t0)dt=0.01;t=t1:dt:t2;n=length(t);x=zeros(1,n);x(1,(-t0-t1)/dt+1)=1/dt;stairs(t,x);axis([t1,t2,0,1.2/dt]) title('单位冲激信号δ(t) ')（4）实验三1234<1>syms tf1=sym('(-t+4)*(u(t)-u(t-4))'); subplot(1,2,1);ezplot(f1);y1=subs(f1,t,-t);f3=f1+y1;subplot(1,2,2);ezplot(f3);function f=u(t) f=(t>0);<2>4、function f=u(t)f=(t>0)syms tf1=sym('(-t+4)*(u(t)-u(t-4))'); subplot(1,3,1);ezplot(f1);f2=sym('sin(2*pi*t)');subplot(1,3,2);ezplot(f2);f6=f1.*f2;subplot(1,3,3);ezplot(f6);5、function f=u(t)f=(t>0)syms tf1=sym('(-t+4)*(u(t)-u(t-4))'); f2=sym('sin(2*pi*t)');subplot(1,3,1);ezplot(f2);f6=f1.*f2;y6=subs(f6,t,t-2);subplot(1,3,2);ezplot(y6);f7=y6+f2;subplot(1,3,3);ezplot(f7);四、t=0:0.1:500;f=100.*abs(sin(2.*pi.*t./50)); plot(t,f,t,fD,t,fA)调用子程序：function fD=fDC(f)fD=mean(f);function fA=fAC(f,fD)fA=f-fD;(5)求解信号的交直流分量代码：function fD=fDC(f)fD=mean(f);function fA=fAC(f,fD)fA=f-fD;t=0:0.1:500;f(t)=100|sin(2*PI*t/50)|;plot(t,fD,t,fA)实验二线性系统时域分析实验报告要求：（1）求解下面两个信号的卷积积分。

实验一连续时间信号的时域表示一、实验目的：1、掌握连续时间信号的MATLAB表示方法；2、掌握用MATLAB描绘二维图像的方法。

二、实验原理：信号是消息的载体，是消息的一种表现形式。

信号可以是多种多样的，通常表现为随时间变化的某些物理量，一般用x(t)或x(n)来表示。

信号按照自变量的取值是否连续可分为连续时间信号和离散时间信号。

连续时间信号是指自变量的取值范围是连续的，且对于一切自变量的取值，除了有若干不连续点以外，信号都有确定的值与之对应。

严格来说，MATLAB并不能处理连续信号，而是用等时间间隔点的样值来近似地表示连续信号。

当取样时间间隔足够小时，这些离散的样值就能较好地近似连续信号。

在MATLAB中通常用向量来表示连续时间信号，向量需要与时间变量相对应。

对于连续时间信号x(t)，可用x、t两个行向量来表示。

其中向量t是形如t=t1:p:t2的MATLAB命令定义的时间范围向量，t1为信号起始时间，t2为终止时间，p为时间间隔。

向量x为连续信号x(t)在向量t所定义的时间点上的样值。

如产生连续信号可用如下命令实现：t =-10:1.5:10;x=sin(t)./ t;在命令窗口（Command Window）中可得到程序执行的结果即x、t的具体值。

注意：在MATLAB程序调试过程中，有时程序执行不出结果或虽然出结果但存在一些问题，MATLAB 都会在Command窗口中给出错误说明，掌握利用Command窗口中的说明检查程序的方法。

用上述向量对连续信号进行表示后，就可以用plot命令绘制信号的时域波形。

命令如下：plot(t,x)title(‘x(t)=Sa(t)’)xlabel(‘t’)axis([-10,10,-0.2,1.2])绘制的信号波形如图一所示，当把t改为：t =-10:0.5:10;则可得到图二。

因为plot命令将点与点之间用直线连接，当点与点之间距离很小时，绘出的图形就成了光滑的曲线。