当前位置：文档之家 › 第二章一维无限势阱模型

第二章一维无限势阱模型

  • 格式：ppt
  • 大小：354.00 KB
  • 文档页数：23

下载文档原格式

  / 23

合集下载

量子力学-第二章-一维势阱

量子力学-第二章-一维势阱

3
时间依赖薛定谔方程
根据能量守恒和时间演化，推导出薛定谔方程。
薛定谔方程的解析解
无限深势阱
假设粒子被限制在一个 无限深的势阱中，无法 逃逸。
波函数的边界条件
在势阱的边界处，波函 数必须满足特定的边界 条件。
波函数的对称性
在势阱中，波函数可能 具有对称或反对称的性 质。
薛定谔方程的数值解
有限差分法
含时薛定谔方程的一维势阱模型
含时薛定谔方程是一维势阱模型中描述粒子动态行为的方 程。该方程包含了时间依赖的势能项，可以描述粒子在时 间演化过程中受到的外部作用力。
含时薛定谔方程的解可以用来研究粒子在一维势阱中的动 态行为，例如粒子在受到激光脉冲作用时的运动轨迹和能 量变化。通过求解含时薛定谔方程，可以深入了解粒子在 一维势阱中的动力学性质。
01
将薛定谔方程转化为差分方程，通过迭代求解。
网格化方法
02
将连续的空间离散化为有限个网格点，对每个网格点上的波函
数进行求解。
量子隧穿效应
03
当势阱深度较小时，粒子有一定的概率隧穿势垒，从势阱中逃
逸。
03
一维势阱中的粒子行为
BIG DATA EMPOWERS TO CREATE A NEW
ERA
粒子在无限深势阱中的行为
时间依赖的一维势阱模型
时间依赖的一维势阱模型描述了粒子在一维空间中受到随时 间变化的势能作用的情况。这种模型可以用来研究粒子在时 间依赖的外部场中的动态行为，例如粒子在激光场中的运动 。
时间依赖的一维势阱模型需要求解含时薛定谔方程，该方程 描述了粒子在时间演化过程中的波函数变化。通过求解含时 薛定谔方程，可以了解粒子在时间依赖的势阱中的动态行为 。

2-6 一维无限深方势阱

2-6 一维无限深方势阱

0 ~ a 上的连续函数，都可以用正弦函数(35)来展开。
从细节上讲， 傅里叶级数是对周期函数进行展开， 所用的三角函数也是定义在无穷区间 上的周期函数。 比如， 已知函数 f x 在 0 ~ a 上的定义， 先将 f x 作奇延拓， 即在 a ~ 0 上，定义 f x f x ，然后将函数以 2a 为周期延拓到整个实轴上。因为是奇函数， 所以傅里叶级数中只出现正弦，基波周期为 2a 。这里我们只关注势阱内部分，将 f x 用 本征函数组(35)展开。当然，也可以对 f x 作偶延拓，再作周期性延拓，这样会得到余弦 级数；或者直接以 a 为周期作周期性延拓，得到标准形式的傅里叶级数，此时基波的周期为

通常把正交性和归一性合并为


ψn x ψm x dx 0
(29)

称本征函数组 ψ n x , n 1, 2, (4) 本征函数组
n


ψn x ψm x dx nm
(30)

是正交归一的。
ψ x , n 1, 2, 是完备的。也就是说，任何在势阱内的连续函数
i
Ent
, x a
(36)
利用欧拉公式，可以将其改写为指数形式
n x, t C1 exp x Ent C2 exp x Ent , x a (37) 2a 2a
1 nπ sin x , ψn x a 2a 0,
势阱宽度仍为 2a ，可以做参数替换 a 为
0 x 2a x 0, x 2a
(33)
a 将势阱宽度变为 a ，此时能级和能量本征函数变 2

量子力学2.6一维无限深势阱

量子力学2.6一维无限深势阱

2008.5
Quantum Mechanics
a、偶宇称态 由于这里内外解
(
2 (x)
x)和 '(
~ cos kx
x)在 | x | a
| x | a 2
处是连续的，
2
更方便的方法是取 ' 连续或 (ln )' 连续。
因此在x
a 处，有 2
ln(cos
kx)
' x a
2
ln(
ex
)
' x
a
，得
2
k tan ka
2
（5）
在x a 处，结果同上。 2
2008.5
Quantum Mechanics
令 则(5)式化为
ka， a
2
2
tan
（6）
（7）
由
2m(V0
E)
,
k
2mE
有
2mV0 2k 2
再利用(6)式,有
2
2
mV0 a 2 2 2
2008.5
(8)
2008.5
Quantum Mechanics
写出分区定态方程 在阱外(经典禁介区)
d2 dx 2
1
2m 2
(V0
E ) 1
0
(1)
令
方程(1)变为
其解为
2m(V0 E)
(2)
1'' 21 0
1 ~ ex
都是方程的解？
2008.5
Quantum Mechanics
考虑到束缚态边界条件：| x | 时 0，有
2008.5
Quantum Mechanics

163一维势阱和势垒问题

163一维势阱和势垒问题
mn
0,
mn mn
克罗内克符号
二、势垒穿透和隧道效应
有限高的方形势垒
数学形式：
U
(
x)
0,
U 0 ,
图形形式：
x 0(P区),x a(S区) 0 x a(Q区)
U
考虑粒子的动能 E小于势垒高
U0
度 U0的情况。（ E < U0 ）
E
PQ S
o ax
U (x) 0, x 0和x a
1
(0 x a)
(x 0及x a)
2
势阱内 0 < x < a
d 2 1
dx2
2E
2
1
0
势阱外 x ≤ 0 ;x ≥a
2 0
理由:因为势壁无限高,所以粒子不能穿透势壁,故势 阱外的 波函数为零
定态薛定谔方程为
d 2
d x2
2E
2
0
E是粒子的总能量，E > 0，令 k
定态薛定谔方程变为
d 2
一维无限深方势阱的图形表达形式 ：
∞∞
U(x)
粒子只能在宽为 a 的两个无限 高势壁间运动，这种势称为一 维无限深方势阱。
0
ax
因为系统的势能与时间无关，因此这是一个定 态问题，可以用定态薛定谔方程进行求解。
2
2
2
U
(r)
(r )
E
(r )
————定态薛定谔方程
①列出各区域的定态薛定谔方程
若在样品与针尖之间
加一微小电压Ub电子 就会穿过电极间的势
垒形成隧道电流。
隧道电流对针尖与样品间的距离十分敏感。 若控制隧道电流不变，则探针在垂直于样品 方向上的高度变化就能反映样品表面的起伏。

2.6一维无限深势阱

2.6一维无限深势阱
2 2
O
a
x
第二章 波函数和薛定谔方程
2/33
Quantum mechanics
2
§2.6 一维无限深势阱
d 2 E 0, (a x a) U 0 , (| x | a) 2 2 dx U ( x) 2 2 d 0, (| x | a) ( E U ) 0, ( x a , x a ) 0 2 dx 2 2 (U 0 E ) 1/ 2 2 E 1/ 2 令： （ 2 ) , [ ] 2
第二章 波函数和薛定谔方程
4/33
Quantum mechanics
§2.6 一维无限深势阱
A sin( x ),(| x | a) 1 x x Be ,( x a), Ce ,( x a) 当x=±a处波函数连续可得: ctg( a ) ,( x a) ctg( a ) ,( x a)
Quantum mechanics
§2.9 例题
例1,设一维无限深方势阱宽度为a,求处于基态的 粒子的动量分布(P39). U(x) 0,(0 x a) 解：U ( x) ,( x 0),( x a)
2 d 2 ( x) E ( x) 0, (0 x a) 2 2 dx ( x) 0, (0 x, x a)
d ctg( x ),(| x | a) dx ,( x a), ,( x a) 0, ctg a , / 2, tg a ,
a A sin a Be ,( x a) A sin x,(| x | a) 0, 0, x a x A sin a Ce ,( x a) Be ,( x a), Ce ,( x a)

2.6 一维无限深势阱

2.6 一维无限深势阱

3.
eiθ = cos θ + i sin θ e −iθ = cos θ − i sin θ
sinθ = ? cosθ = ?
4.束缚态及其能量特点 5.波函数的宇称及其与 势的关系 6.基态？
标准条件（1）：单值，只有一个解，满足 标准条件（2）：有限，x ≥ a ，ψ 有限要求 得出 Ψ=0 。 标准条件（3）：连续：
ψ ( − a ) = ψ ( a ) =
0 0
x = − a时 x = a时
A sin αa + B cos αa = 0 − A sin αa + B cos αa = 0
6.归一化常数，波函数 归一化常数， 归一化常数
2组 解 0 x ≥a ψn = nπ Asi n x 2a 和 0 x ≥a ψn = nπ Bcos x 2a 或 并 一 式 合 为 个 子 0 x ≥a ψn = ' nπ A si n (x + a) 2a
A和B不能同时为0，否则Ψ到处为0.
(1) A = 0 , ( 2 ) B = 0, n sin αa = 0 αa = π 2
(n = ±1,±3,±5 L ) (n = 0,±2,±4,±6 L )
n=0？负整数？A、B同时为0？ A、B同时不为0？ 所以，n只需取正整数。
用 Schrodinger 方程处理一类简单问题——一维定态问题：
（1）有助于具体理解已学过的基本原理； （2）有助于进一步阐明其他基本原理； 3 （3）处理一维问题，数学简单，从而能对结果进行细致讨论， 量子体系的许多特征都可以在这些一维问题中展现出来； （4）一维问题是处理各种复杂问题的基础。
§2.6

一维无限势阱

一维无限势阱

一维无限深势阱定义编辑粒子在一种简单外力场中做一维运动，其势能函数为U(X)=0 （-a<x<a)；U(x)=∞ (x≥a或x≤-a)。

由于其函数图形像阱，且势能在一定区域为0，而在此区域外势能为无穷大，所以这种势能分布叫做一维无限深势阱。

实际模型编辑自由电子在一块金属中的运动相当于在势阱中的运动。

在阱内，由于势能为零，粒子受到的总的力为零，其运动是自由的。

在边界上x=0或x=a处，由于势能突然增加到无限大，粒子受到无限大指向阱内的力。

因此，粒子的位置不可能到达0<x<a的范围以外。

一维无限深势阱中粒子运动的波函数编辑一维无限深势阱中粒子运动的波函数为Ψ(x)=√(2/a)·sin(nπx/a) (0<x<a)。

三、一维势阱3.1 一维无限深势阱要使电子脱离金属，需要对它做功，这相当于电子在金属表面处势能突然增大，自由电子在金属内部的运动，可近似比作在无限深势阱的运动。

由于金属是各向同性的，便可简化为电子在一维无限深势阱中的运动。

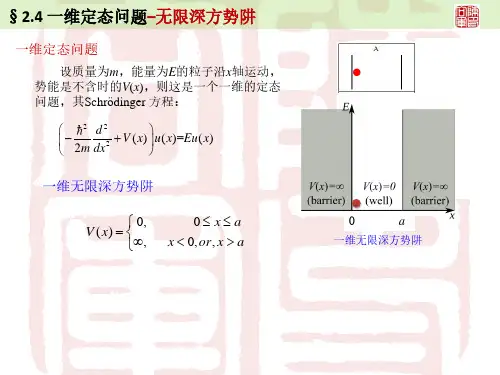
势能曲线如右图，势能表达式为电子在一维无限深势阱中运动，用经典力学描述和量子力学描述得到了完全不同的结果。

按照经典概念，当外界向它提供能量时，电子可获得此能量而自身能量发生连续变化。

电子在阱内任何位置出现的概率也是相等的。

然而，按照量子力学观点，它的行为却不是这样的。

(1) 定态薛定谔方程的解电子所受的保守力，在边界处电子所受的力无限大，指向阱内，意味着电子不可能越出阱外，由波函数物理意义可知势阱外波函数。

电子在势阱内势能为零，受力为零。

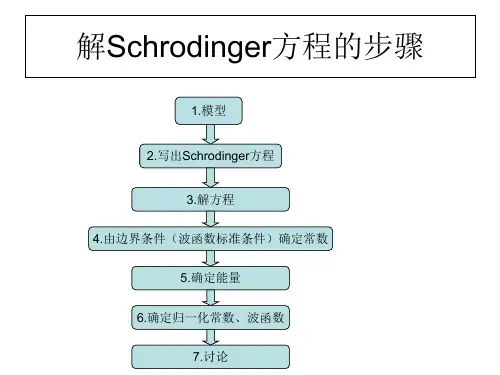
势阱内定态薛定谔方程为令方程变为其解为根据波函数应满足的标准化条件，波函数应在边界x=0和x=a上连续得应用归一化条件求得于是定态波函数为(2) 能量量子化因，合并(23.3.3)式，即得到一维无限深势阱中的电子能量上式表明：电子的能量不能连续地取任意值，只能取分立值，即能量是量子化的，可形象地称为处于相应的能级(如右图所示)。

2.5-2.6 一维无限深势阱

2.5-2.6 一维无限深势阱

也可看出，作用于任一波函数Ψ上的二算符 i 是相当的。这 t 2 两个算符都称 2 ˆ V H 为能量算符。 2
（2）能量本征值方程
将
[
2 V ] E 2
改写 成
ˆ E H
一个算符作用于一个函数上得到一个常数乘以该函数这与数学 物理方法中的本征值方程相似。 数学物理方法中：微分方程 + 边界条件构成本征值问题；
i E t [ 2 V ] E 2
e xp[ iEt / ] d i f ( t ) Ef ( t ) dt 2 [ 2 V ] ( r ) E ( r ) 2


i [ n ( r ) n ( r ) n ( r ) n ( r )] 2
J n (r )
§2.6 一维无限深势阱
2008.5
Quantum Mechanics
金属中的电子在构成金属骨架的晶体点阵之 间运动时，要受到点阵上正离子的作用力， 这种作用力可用两者相互作用的势能表征。 电子在这个有势力场中运动时，通常并不能 自发地挣脱出金属表面，这表明在金属内的 电子运动到表面上时，它的总能量（动能和 势能）远小于表面处的势能，因而受到阻挡。 因此，我们对金属中的电子运动有时可以作 这样的简化处理，即认为：如果没有外界影 响（如外电场、光照等），电子好似被无限 高的势能“壁”禁囿于金属内，并在一维势 力场作用下运动着，这个抽象出来的计算模 型，称为一维无限深方形势阱，简称一维方 势阱。
求解定态问题的步骤
1.模型
2.写出Schrodinger方程 3.解方程
4.由边界条件（波函数标准条件）确定常数

一维定态问题无限深方势阱

一维定态问题无限深方势阱
(1) 粒子的位置 r
例如：一维无限深方势阱
粒子的位置是不确定的，取值在[0, a]之间。 但粒子的概率分布是确定的，是
u(x)
2
=
2 sin2 nπ a a 0
x, ,
0≤ x≤a x < 0,or, x > a
n = 1, 2,3,
所以，可以得到粒子位置的平均值 (假设粒子处在基态 n =1 态)：
Spherical coordinates
(r,θ ,ϕ )
x = r sinθ cosϕ y = r sinθ sinϕ z = r cosθ
r = x2 + y2 + z2
θ = arccos
z
x2 + y2 + z2
ϕ = arctan y
x
§2.5 力学量的平均值、算符表示—算符表示
角动量算符 Lˆ= r × pˆ 在球坐标系中的三个分量为
§2.5 力学量的平均值、算符表示—平均值
粒子在外场 V(r)中运动，体系的
定态薛定谔方程：
−
2
2m
∇2
+
V
(r)
u (r)=Eu (r)
求解该方程，可以得到体系的波函数和能量E。
例如：粒子束缚在一维无限深方势阱中
波函数 能量
u(x)
=
2 sin nπ x , a a,
0
En
=
π2 2
则V(r, t)的平均值为：
∫ ∫ +∞
= V (r,t) = V (r,t)ρ (r,t)dτ
+∞
ψ
*
(r
,
t
)V
(r

量子力学_第二章_一维势阱

量子力学_第二章_一维势阱

（四）讨论
一维无限深 势阱中粒子 的状态
0 n 1 n sin x 2a a 1 n cos x 2a a 其能量本征值为： n 2 2 2 En 8 a
| x | a; n even, n odd, | x | a; | x | a .
2 d 2 [ V1 ( x )]X ( x ) E x X ( x ) 2 dx2 2 d 2 [ V2 ( y )] ( y ) E yY ( y ) Y 2 dy2 2 d 2 [ V3 ( z )]Z ( z ) E z Z ( z ) 2 dz2
2
n为正偶数， x a
x a
n为正奇数，
x a
x a
由归一化条件
-
n dx 1 A'
1 a
.
一维无限深方势阱中 粒子的定态波函数为： n ( x, t ) n (x)e
-i En t -i
En t n A' sin ( x a )e 2a e i e i 用公式sin 2i
等式两边除以 （x, y, z ) X ( x )Y ( y ) Z ( z )
1 X 1 2 d 2 X V1 ( x ) 2 dx2 Y 1 2 d 2 Y V2 ( y ) 2 dy2 Z 2 d 2 Z V3 ( z ) E 2 dz2
I II III
0
a
ψ 有限条件要求 C2=0。
d2 2 dx d2 2 dx d2 2 dx
I
2 2
I
0 0 0
II

第二章一维无限势阱模型

第二章一维无限势阱模型
dt
Hˆ(r) E(r)
E是不依赖r和t的常数
i df Ef
f (t) C exp[iEt / ]
dt
体系处于
(r,t)
(r)
exp[
iEt
/
]
所描写的状态时
能量有确定的值，称这种状态为定态
在分离变量过程中引入的常数 E 为粒子的能量
(r,t) (r) exp[iEt / ] 定态波函数
1 一维线性谐振子 如果粒子的势能具有如下形式 U (x) 1 m 2 x2
2
这样绕平衡位置做周期性振动的粒子称为一维线性谐振子
➢ 任何在平衡位置附近的微振动(三维振动)都可以分解成 几个独立的一维谐振子
➢ 固体中原子的振动可以用这种模型近似地研究
➢ 晶体中格点的振动、分子与分子间的互作用势、核子之 间的核力势等等都可近似为线性谐振子问题
• 在粒子能量E<<U0时的情况下，透射系数不为零经典理论无 法解释。
入射波＋反射波
U(x)
透射波
x
隧道效应的实质
1 隧道效应
• 粒子能量小于势垒高度时仍能贯穿势垒的现象 • 类似一列火车通过隧道穿过山峰，这里不存在有形的山峰， 只存在一条无形的势垒曲线
2 原因
微观粒子具有波动、粒子二象性；波原则上可以透过不同物理 性质的两空间的界面，例如，光波的透射
1 0
由定态波函数的边界条件
x a
(U )
1(a) 2 (a),1(a) 2 (a)
4 薛定谔方程的解
首先，引入符号
定态薛氏方程化为
2mE 2
1/ 2
d 2(x) 2(x) 0
dx 2
它的解为
2 Asin x B cosx

一维无限深势阱ppt课件

一维无限深势阱ppt课件

n个节点。
四.几率分布:
在经典力学中,在ξ到ξ+dξ之间的区域内找到质点的 11
几率ω (ξ) dξ与质点在此区域内逗留的时间dt成
比例:
( )d dt
T
T是振动周期。因此有
( )
T
1
d
dt
1 vt
即几率密度与质点的速度成反比。对于经典的线性谐振子，ξ= a sin(ωt+δ ) ,在ξ点的速度为
J
i
2
[
i
d dx
* i
* i
d dx
i
]
k1
|
A |2
JD
k1
| c |2 ,
JR
k1
|
A |2
16
透射系数与反射系数为：
D
JD J
(k12
4k12k22 k22 )2 sin 2 k2a 4k12k22
R
JR J
(k12
(k12 k22 )2 sin 2 k2a k22 )2 sin 2 k2a 4k12k22
13
如果将此问题推广到三维，显然它是散射问题。
二、方势垒的穿透 (1)E>U0 的情况：
薛定谔方程为
d 2
dx 2
2
2
(E
U
0
)
0
令 k1 2E / 2
则其解为
k2 2 (E U 0 ) / 2
1 Aeik1x Ae ik1x
x0
2 Beik2x Beik2x 0 x a
3 Ceik1x C e ik1x
数为：
2 2[U ( x)E ]dx
D D0e
贯穿势垒U(x)的透射系数应等于贯穿所有这些方形势垒的透射 系数之积，即

一维无限深方势阱中势阱中粒子的能级公式推导

一维无限深方势阱中势阱中粒子的能级公式推导

一维无限深方势阱中势阱中粒子的能级公式推导一维无限深方势阱是量子力学教学中常见的模型之一。

在这个模型中，粒子被限制在一个长度为L的势阱中运动，势阱的势能在阱内为零，而在阱外则无限大。

研究一维无限深方势阱中粒子的能级公式推导，可以帮助我们更深入地理解量子力学中的基本概念和数学工具。

下面我将按照深度和广度的要求，从简单的物理概念和数学原理开始，逐步推导一维无限深方势阱中粒子的能级公式，并带有个人的观点和理解。

一、基本概念和数学工具1.1 势阱势阱是一种常见的量子力学模型，它可以用来描述粒子在受限空间中的运动。

在一维无限深方势阱中，势能在阱内为零，而在阱外为无限大，这意味着粒子在阱内具有确定的能量，而在阱外无法存在。

1.2 薛定谔方程薛定谔方程是描述量子力学中粒子运动的基本方程。

对于一维无限深方势阱而言，薛定谔方程可以简化为一维定态薛定谔方程：\[ -\frac{\hbar^2}{2m}\frac{d^2\psi(x)}{dx^2} = E\psi(x) \]其中，ψ(x)是粒子的波函数，m是粒子的质量，E是粒子的能量，ħ是普朗克常数。

二、能级公式的推导2.1 边界条件在一维无限深方势阱中，粒子受到势阱两侧的限制，因此波函数在势阱边界处为零。

这意味着在x=0和x=L处，波函数满足边界条件：\[ \psi(0) = 0 \]\[ \psi(L) = 0 \]2.2 波函数的解根据边界条件，我们可以求解一维定态薛定谔方程得到波函数的解。

波函数的解具有以下形式：\[ \psi_n(x) = \sqrt{\frac{2}{L}}\sin(\frac{n\pi x}{L}) \]其中，n为能级量子数。

2.3 能级公式将波函数的解代入一维定态薛定谔方程中，可以得到粒子的能级公式：\[ E_n = \frac{n^2\pi^2\hbar^2}{2mL^2} \]其中，En为粒子的能量，n为能级量子数。

三、个人观点和理解在推导一维无限深方势阱中粒子的能级公式过程中，我们利用了量子力学基本的数学工具和物理概念，如薛定谔方程、波函数和边界条件。

一维无限深势阱

一维无限深势阱

2008.5
25
对奇宇称态则不同，只当
2 2 mV0a2 / 22 2 / 4
即
V0a2
2h2
2m
，或
V0
2h2
2ma2
时
才可能出现最低的奇宇称能级。
2008.5
26
3、束缚态与分立谱的讨论
由以上分析可知，束缚态能量是分立的。
相应动量也是分立的。 这是在束缚态边界条件下求解定态方程的结果。
En
π 22 2ma 2
n2
(n 1,2,3, )
2008.5
8
❖ 由波函数的归一性质定常数 B
a
(x) *(x)dx 1
0
a
B2sin 2kxdx 1
0
得
B 2 a
本征函数
n(x)
2 sin nπ x aa
( n 1,2,3,)
这组函数构成本征函数系。
2008.5
9
⑥定态波函数
n
n
2008.5
16
写出分区定态方程 在阱外(经典禁介区)
d2 dx 2
1
2m 2
(V0
E) 1
0
(1)
令
方程(1)变为
其解为
2m(V0 E)
(2)
1'' 21 0
1 ~ ex
都是方程的解？
2008.5
17
考虑到束缚态边界条件：| x | 时 0，有
Be
x
1(x)
Aex
A, B为待定常数.
0时， ' ' 0，
取极小值 向上弯曲
0时， ' ' 0，
取极大值 向下弯曲（见右图）

一维势阱

一维势阱

， n = 1, 2, 3, …
试计算n = 1时，在 x1 = a/4 →x2 = 3a/4 区间找到粒子的 概率．
解：找到粒子的概率为
3a / 4
2 2 x ( x) 1 ( x) d x sin d x a a a/4 a/4
* 1
3a / 4
2 x ) 3 a 1 cos( 1 1 a 4 a dx a 2 π 4
0,
讨论：
2 k 2 22n2 ① 粒子的能量 E n , n 1,2,3, 2 2 2 a
粒子的最低能量状态称为基态，则一维无限深方势 阱的基态能量为：
E1 2 0 2 a
2 2
————零点能
与零点能相对应的，应存在零点运动。这与经典粒 子的运动是相矛盾的。零点能是微观粒子波动性的表 现，因为“静止的波”是没有意义的。
3 n 3
4
n4
x a
a x
第k激发态(n=k+1)有k个节点。
（2）一维无限深势阱的粒子位置概率密度分 布 2
1
n 1
0 2
2
x a n2 x a
a x
0 n3 3
2
0 4 0
2
n4
x a
n时
量子经典
|n | 2
n很大
En
0
a
一维无限深势阱
En n
n ( x)
h 2 En ( x ) n 2 8ma
2 n n ( x) sin x a a
2ห้องสมุดไป่ตู้
2 2 n n ( x ) sin ( x ) a a
0
a
x
例1: 证明无限深方势阱中，不同能级的粒子波函数 具有正交性：

第二章 -.6一维无限深势阱

第二章 -.6一维无限深势阱

可见， 取负整数与正整数描写同一状态。 可见，n取负整数与正整数描写同一状态。
（3）n = 0 , E = 0, ψ = 0，态不存在，无意义。 ） ，态不存在，无意义。 而n = ± k, k=1,2,...
（4）波函数宇称
ψ ψ n(−x) = − n(x) ψ ψ n(−x) = + n(x)
I
( − a ) = li m C 1 e − β a = 0
β → ∞
I
所 以
ψ
= 0
ψ ψ ψ
I II III
= C 1e
βx
+ C 2e − βx + B 2e − βx
ψI =0
ψ III = 0
=0。 B1=0。
− E )
= A sin( α x + δ ) = B 1e
βx
βx
+ C 2e − βx + B 2e − βx
= A sin( α x + δ ) = B 1e
βx
考虑波函数三个标准条件 1。单值 2。有限 3、连续
有限的条件， 当x → - ∞ , ψ 有限的条件，要求
=0。 C2=0。
ψ
I
= C 1e βx
2
又 由 于 β
=
2 µ (V h 2
ψ
− E )
U0 → ∞
边界条件
ψ 根据波函数连续、有限的条件。 = 0
证明见附录I， 令
x ≥a
2mE α= h2
d 2ψ ∴由(1) + α 2ψ = 0 dx 2 ψ = A sin αx + B cos αx
x <a x <a
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

2 2 U (r) E
2m
定态薛定谔方程
2 定态薛氏方程的边界条件和波函数满足的条件
边界条件： 在不同势能区域之间的边界上波函数连续，在有限势 能边界上波函数对空间坐标的一阶微商连续
波函数满足的条件：
1）归一化条件： (x) 2 1
2）束缚态条件： lim (x) 0 x
3 本征值、本征函数 eigenfunction
• 若一个算符作用在波函数上得出一个常数乘以该波函
数 ，如 Fˆ n fn n ，则称此方程为该算符的本征方程，
称此常数fn为算符F的第n个本征值，波函数为fn相应的本 征波函数
例如哈密顿算符
Hˆ 2 2 U (r) 2m
定态薛定谔方程 Hˆ E 就是哈密顿算符的
本征值方程，E 称为哈密顿算符的本征值，(r,t)
• 双原子分子的两原子间的相互作用
U(x)
势能U(x)可在平衡位置展开为
aa x
两原子间的互作用能
U U0 k(x a)2 / 2
k
2U x 2
xa
式中k和U0都是常量
x=a是一个稳定的平衡点
一般来说，一个体系在平衡点附近的行为，都可近似 为一维线性谐振子问题
2 线性谐振子的能量本征值
谐振子的能级
a 2a 2
束缚态 基态 宇称
1 束缚态 bound state
• 束缚态：粒子只能束缚在有限区域内，在无限远处波函数 为零的状态（断续谱）
• 非束缚态：在无穷远处发现该粒子的概率不为零（连续谱）
• 一维无限势阱中给出的波函数全部是束缚态
2 基态 ground state
• 粒子能量最低的本征态
•
• 常常遇到微观粒子的势能函数 U 与时间 t无关的稳定
的势场问题，这称为定态问题
自由运动粒子………… U = 0
氢原子中的电子……
U r 1 e2
40 r
1 定态薛定谔方程的建立
用分离变量法求解薛定谔方程的特解
设 (r,t) (r) f (t)
i d (r,t) Hˆ (r,t)
a 2a 2
定态薛定谔方程
定态薛定谔方程 定态波函数
2 2 U (r) E
2m
(r,t) (r) exp[iEt / ]
边界条件：波函数及其一阶微商连续
波函数满足的条件：
(x) 2 1
lim (x) 0
x
解
确定粒子势能的表达式
题
思
能量的本征值和本征函数
路
能量本征函数归一化
列出定态薛氏方程 引入参数 化简方程
a 2a
我们称这时波函数具有偶宇称
当n为偶数时 n (x) n (x)
我们称这时波函数具有奇宇称
• 并非所有的函数都有确定的宇称
• 在一维情况下，只有在势能函数具有空间反演对称性： U(x)=U(-x)，是x的偶函数时，波函数才有确定的宇称
一维线性谐振子模型
• 分子中的原子或晶格点阵上的原子都可以近似地看作处在 以平衡位置为中心的弹性力场中。按经典力学，它们将以一 定的频率围绕平衡位置做简谐振动。
解：利用坐标和动量的不确定关系 x2 p2 2
4
谐振子的能量不确定度为：
E p2 1 m 2 x2
2m 228mx2源自1 2m 2 x2
使ΔE取极小值条件
dE
d x 2
1 m 2
2
2
8mx4
谐振零点能为
E
44 2
x2
2m
隧道效应 tunneling effect
1. 势垒
设有一定能量E的粒子，沿x轴方向射向势垒
求出方程的通解
波函数边界条件
一维无限深势阱
定态薛定谔方程
2 2m
d
22 (x)
dx2
E2
(x)
2mE 2
1/ 2
能量本征值
En
n2 22
8ma2
n2 E1
(n 1,2,3, )
n
A sin
n
2a
(x a),
n为正整数， x a
0 x a
nndx
1
能量本征函数
n (x)
1 sin( n x n )
• 在粒子能量E<<U0时的情况下，透射系数不为零经典理论无 法解释。
入射波＋反射波
U(x)
透射波
x
隧道效应的实质
1 隧道效应
• 粒子能量小于势垒高度时仍能贯穿势垒的现象 • 类似一列火车通过隧道穿过山峰，这里不存在有形的山峰， 只存在一条无形的势垒曲线
2 原因
微观粒子具有波动、粒子二象性；波原则上可以透过不同物理 性质的两空间的界面，例如，光波的透射
n
A sin
n
2a
(x
a),
n为正整数， x a
0 x a
因为
2mE 2
1/ 2
n (n 1,2...)
2a
En
n2 22
8ma2
n2 E1
(n 1,2,3, )
常数A可由归一化条件,确定
nndx 1
请同学们自己试一试
能量本征函数
n (x)
1 sin( n x n )
称为哈密顿算符的本征波函数(能量本征态)
一维无限势阱模型
1 一维无限深方势阱 square potential well
粒子的势能具有如下形式
0 (a x a) U (x) ( x a)
U→∞ U(x) U→∞
• 是一个理想模型，适 用于原子内层的电子、原
子核中的质子
U=0
Ⅰa Ⅱ a Ⅲ x
因此线性谐振子具有分立的能级为
En
(n
1 )
2
n=0,1,2…
U(x)
E
n2
n0
x
相邻两能级间距 E En1 En
基态能量 E0 / 2 零点能
谐振子的基态能量不为零，是微观粒子波动性的体现
静止的波是不存在的
如果不考虑零点能，谐振子的能量 量子化的假说
En
n,验证了Planck
例题
利用不确定关系估算谐振子的零点能
思考：若势能U(x)改变一个常数C,即U(x) U(x)＋C，粒子 能量本征值是否改变？能量的本征函数是否改变？
作业题：讲义P76，第22、23题
思考题： 经典谐振子和量子谐振子的区别 作业题：讲义P76，第7、27题；
1 能量为1eV的电子遇到宽度为0.1nm，高度为2eV的势垒， 电子穿过势垒的概率是多少？
作业：
1 一维无限势阱，粒子的势能为
U
(x)
0
(0 x a) (x a, x 0)
求粒子的本征能量和本征函数
2 设有一电子在宽为0.20nm的一维无限势阱中，计算
(1) 电子在最低能级的能量，（2）当电子在第一激发态(n=2)时 在势阱中何处出现的几率最小，其值为多少？
3 讲义P75，第20题
第二章 定态薛定谔方程
定态薛定谔方程 一维无限势阱模型 一维线性谐振子模型 隧道效应(势垒贯穿)
定态薛定谔方程
• 薛定谔方程是描述体系的状态如何随时间变化 • 特殊的状态，就是能量取确定值的状态，称之为稳定状态，
简称定态 stationary state • 定态下，能量的取值不随时间的变化而改变 • 描述定态的波函数称为定态波函数 • 定态波函数满足的薛定谔方程称为定态薛定谔方程
U(x) U0
U0,0 x a;
U (x)=
1 23
0a
x
0, x 0, x a,
经典力学： 若E<U0，则粒子不能进入势垒，将全部被弹回去 若E>U0，则粒子将穿过势垒
量子力学：不论粒子的能量为何值，将按一定的几率穿透势垒、 也可以按一定的几率被势垒反射
•粒子的能量E<<U0时，透射系数随势垒宽度的加宽而指数下降。
一维无限势阱中的粒子，阱内粒子的最低能量
E1
22
8ma2
n=1的本征态为基态
• 一维线性谐振子的基态为n=0的本征态
3 宇称 parity
由一维无限势阱的本征态，可以证明
当n为奇数时 n (x) n (x)
n (x)
1 sin nx , n 2,4,6...
a 2a
1 cos nx , n 1,2,3...
dt
Hˆ(r) E(r)
E是不依赖r和t的常数
i df Ef
f (t) C exp[iEt / ]
dt
体系处于
(r,t)
(r)
exp[
iEt
/
]
所描写的状态时
能量有确定的值，称这种状态为定态
在分离变量过程中引入的常数 E 为粒子的能量
(r,t) (r) exp[iEt / ] 定态波函数
无限深方势阱
• 阱指的是势能曲线的 形状，是无形的阱
• 波函数在势阱之外为零
2 一维无限势阱的定态薛氏方程
在阱内(-a < x < a)
2 2m
d
22 (x)
dx2
E2 (x)
在阱外(x -a, x a)
2 2m
d
21 ( x)
dx2
U1 ( x)
E1(x)
3 边界条件
在 阱外U→∞，所以有
A、B不能同时为零
sin a 0
或
cosa 0
当 cosa 0
n (n为奇数)
2a
同时有 A 0
第一组
n
B cos
n
2a
x,
n为奇数， x a
0 x a