《流体力学》第三章流体动力学基础例题

第三章 流体动力学基础3－1 已知速度场为k z x j y x i y x u)()()(2-+-++= (m/s)，求(2，3，1)点的速度和加速度。

已已知知：：z x u y x u y x u -=-=+=z y x )(2，， 解析：(1) (2，3，1)点的速度为m/s 1m/s 1m/s 10)(2z y x =-=-=-==+=z x u y x u y x u ，， s /m 10.101)1(102222z 2y 2x =+-+=++=u u u u (2) (2，3，1)点的加速度为2x z x y x x x x m/s 1832262602)(2)(20=⨯+⨯=+=+⨯-+⨯++=∂∂+∂∂+∂∂+∂∂=y x y x y x zuu y u u x u u u a τ2y zy yy xy y m/s 1133230)1()(1)(20=⨯+=+=+-⨯-+⨯++=∂∂+∂∂+∂∂+∂∂=y x y x y x zu u yu u xu u u a τ2z z z y z x z z m/s 913222)1()(01)(20=+⨯+=++=-⨯-++⨯++=∂∂+∂∂+∂∂+∂∂=z y x z x y x zu u y u u x u u u a τ22222z 2y 2x s /m 93.2291118=++=++=a a a a3－2 已知速度场为k z y j y i x u )34()(2)3(2-+-++=ττ (m/s)，求τ＝2秒时，位于(2，2，1)点的速度和加速度。

已已知知：：z y u y u x u )34()(23z 2y x -=-=+=，，ττ解析：(1) τ=2秒、位于(2，2，1)点的速度为m/s 5)34(m/s 4)(2m/s 83z 2y x =-=-=-==+=z y u y u x u ，，ττ s /m 25.105)4(82222z 2y 2x =+-+=++=u u u u (2) τ=2秒、位于(2，2，1)点的加速度为2x z x y x x x x m/s 251)223(31)3(3003)3(1=++⨯⨯=++=++⨯++=∂∂+∂∂+∂∂+∂∂=τττx x zuu y u u x u u u a2222y zy yy xy y m/s 342)22(282)(80)4()(202=+-⨯⨯=+-=+-⨯-++=∂∂+∂∂+∂∂+∂∂=τττy y y y zu u yu u xu u u a2222222z z z y z x z z m/s 91)324()22(18)34()(8)34(4)(200=⨯-⨯+-⨯⨯=-+-=-+⨯-++=∂∂+∂∂+∂∂+∂∂=z y y z zy z y zuu y u u x u u u a τττ22222z 2y 2x s /m 15.4393425=++=++=a a a a3－3 已知二维流场的速度分布为j x y i x y uττ)96()64(-+-= (m/s)。

第三章 流体运动学3-1粘性流体平面定常流动中是否存在流函数？ 答：对于粘性流体定常平面流动，连续方程为：()()0=∂∂+∂∂yv x u ρρ； 存在函数：v t y x P ρ-=),,(和()u t y x Q ρ=,,，并且满足条件：()()yP x Q ∂∂=∂∂。

因此，存在流函数，且为：()()()dy u dx v Qdy Pdx t y x ρρψ+-=+=⎰⎰,,。

3-2轴对称流动中流函数是否满足拉普拉斯方程?答：如果流体为不可压缩流体，流动为无旋流动，那么流函数为调和函数，满足拉普拉斯方程。

3-3 就下面两种平面不可压缩流场的速度分布分别求加速度。

（1）22222 ,2yx ym v y x x m u +⋅=+⋅=ππ （2）()()()222222222 ,yxKtxyv yxx y Kt u +-=+-=，其中m ，K 为常数。

答：（1）流场的加速度表达式为：yv v x v u t v a y u v x u u t u a x ∂∂+∂∂+∂∂=∂∂+∂∂+∂∂=y ,。

由速度分布，可以计算得到：0 ,0=∂∂=∂∂tvt u ，因此： ()222222y x x y m x u +-⋅=∂∂π，()22222y x xy m y u +-⋅=∂∂π；()22222y x xy m x v +-⋅=∂∂π，()222222y x y x m y v +-⋅=∂∂π。

代入到加速度表达式中：()()()22222222222222222222220y x x m y x xym y x y m y x x y m y x x m a x +⋅⎪⎭⎫⎝⎛-=+-⋅⋅+⋅++-⋅⋅+⋅+=πππππ()()()22222222222222222222220y x y m y x y x m y x y m y x xym y x x m a y +⋅⎪⎭⎫⎝⎛-=+-⋅⋅+⋅++-⋅⋅+⋅+=πππππ（2）由速度分布函数可以得到：()()()322222222 ,y x Kxyt v y x x y K t u +-=∂∂+-=∂∂ ()()3222232y x y x Ktx x u +-⋅=∂∂，()()3222232y x y x Kty y u +-⋅=∂∂； ()()3222232y x x y Kty x v +-⋅-=∂∂，()()3222232yx y x Ktx y v +-⋅-=∂∂。

一元流体动力学基础1.直径为150mm 的给水管道，输水量为h kN /7.980，试求断面平均流速。

解：由流量公式vA Q ρ= 注意：()vA Q s kg h kN ρ=⇒→//A Qv ρ=得：s m v /57.1=2.断面为300mm ×400mm 的矩形风道,风量为2700m 3/h,求平均流速.如风道出口处断面收缩为150mm ×400mm,求该断面的平均流速 解：由流量公式vA Q = 得：A Q v =由连续性方程知2211A v A v = 得：s m v /5.122=3.水从水箱流经直径d 1=10cm,d 2=5cm,d 3=2.5cm 的管道流入大气中. 当出口流速10m/ 时,求(1)容积流量及质量流量;(2)1d 及2d 管段的流速解：(1)由s m A v Q /0049.0333==质量流量s kg Q /9.4=ρ (2)由连续性方程：33223311,A v A v A v A v ==得：s m v s m v /5.2,/625.021==4.设计输水量为h kg /294210的给水管道，流速限制在9.0∽s m /4.1之间。

试确定管道直径，根据所选直径求流速。

直径应是mm 50的倍数。

解：vA Q ρ= 将9.0=v ∽s m /4.1代入得343.0=d ∽m 275.0 ∵直径是mm 50的倍数，所以取m d 3.0= 代入vA Q ρ= 得m v 18.1=5.圆形风道，流量是10000m 3/h,，流速不超过20 m/s 。

试设计直径，根据所定直径求流速。

直径规定为50 mm 的倍数。

解：vA Q = 将s m v /20≤代入得：mm d 5.420≥ 取mm d 450= 代入vA Q = 得：s m v /5.17=6.在直径为d 圆形风道断面上，用下法选定五个点，以测局部风速。

设想用和管轴同心但不同半径的圆周，将全部断面分为中间是圆，其他是圆环的五个面积相等的部分。

第1章 绪论1.1 若某种牌号的汽油的重度γ为7000N/m 3，求它的密度ρ。

解：由g γρ=得，3327000N/m 714.29kg/m 9.8m /m γρ===g1.2 已知水的密度ρ=997.0kg/m 3，运动黏度ν=0.893×10-6m 2/s ，求它的动力黏度μ。

解：ρμ=v 得，3624997.0kg/m 0.89310m /s 8.910Pa s μρν--==⨯⨯=⨯⋅ 1.3 一块可动平板与另一块不动平板同时浸在某种液体中，它们之间的距离为0.5mm ，可动板若以 0.25m/s 的速度移动，为了维持这个速度需要单位面积上的作用力为2N/m 2，求这两块平板间流体的动力黏度μ。

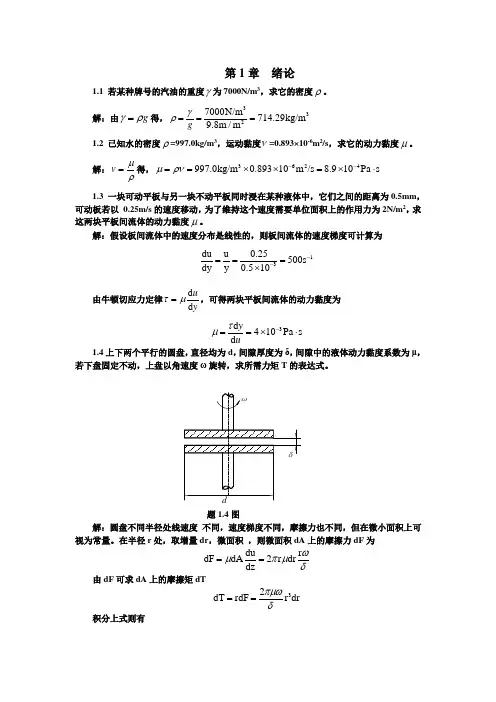
解：假设板间流体中的速度分布是线性的，则板间流体的速度梯度可计算为13du u 0.25500s dy y 0.510--===⨯ 由牛顿切应力定律d d uyτμ=，可得两块平板间流体的动力黏度为 3d 410Pa s d yuτμ-==⨯⋅1.4上下两个平行的圆盘，直径均为d ，间隙厚度为δ，间隙中的液体动力黏度系数为μ，若下盘固定不动，上盘以角速度ω旋转，求所需力矩T 的表达式。

题1.4图解：圆盘不同半径处线速度 不同，速度梯度不同，摩擦力也不同，但在微小面积上可视为常量。

在半径r 处，取增量dr ，微面积 ，则微面积dA 上的摩擦力dF 为du r dF dA2r dr dz ωμπμδ== 由dF 可求dA 上的摩擦矩dT32dT rdF r dr πμωδ==积分上式则有d 43202d T dT r dr 32πμωπμωδδ===⎰⎰1.5 如下图所示，水流在平板上运动，靠近板壁附近的流速呈抛物线形分布，E 点为抛物线端点，E 点处0d =y u ，水的运动黏度ν=1.0×10-6m 2/s ，试求y =0，2，4cm 处的切应力。

（提示：先设流速分布C By Ay u ++=2，利用给定的条件确定待定常数A 、B 、C ）题1.5图解：以D 点为原点建立坐标系，设流速分布C By Ay u ++=2，由已知条件得C=0,A=-625,B=50则2u 625y 50y =-+ 由切应力公式du dy τμ=得du(1250y 50)dyτμρν==-+ y=0cm 时，221510N /m τ-=⨯；y=2cm 时，222 2.510N /m τ-=⨯；y=4cm 时，30τ= 1.6 某流体在圆筒形容器中。

第三章流体动力学基础习题一、单选题1、在稳定流动中，在任一点处速度矢量是恒定不变的，那么流体质点是〔〕 A ．加速运动 B ．减速运动 C ．匀速运动 D ．不能确定2、血管中血液流动的流量受血管内径影响很大。

如果血管内径减少一半，其血液的流量将变为原来的〔〕倍。

A ．21B ．41C ．81D ．1613、人在静息状态时，整个心动周期内主动脉血流平均速度为0.2 m/s ，其内径d =2×10-2m ，已知血液的粘度η =3.0×10-3 Pa·S ，密度ρ=1.05×103 kg/m 3，则此时主动脉中血液的流动形态处于〔〕状态。

A ．层流B ．湍流C ．层流或湍流D ．无法确定4、正常情况下，人的小动脉半径约为3mm ，血液的平均速度为20cm/s ，若小动脉某部分被一硬斑阻塞使之变窄，半径变为2mm ，则此段的平均流速为〔〕m/s 。

A ．30B ．40C ．45D ．605、有水在同一水平管道中流动，已知A 处的横截面积为S A =10cm 2，B 处的横截面积为S B =5cm 2，A 、B 两点压强差为1500Pa ，则A 处的流速为〔〕。

A ．1m /sB ．2m /sC ．3 m /sD ．4 m /s6、有水在一水平管道中流动，已知A 处的横截面积为S A =10cm 2，B 处的横截面积为S B =5cm 2，A 、B 两点压强之差为1500Pa ，则管道中的体积流量为〔 〕。

A ．1×10-3 m 3/sB ．2×10-3 m 3/sC ．1×10-4 m 3/sD ．2×10-4 m 3/s7、通常情况下，人的小动脉内径约为6mm ，血流的平均流速为20cm/s ，若小动脉某处被一硬斑阻塞而变窄，测得此处血流的平均流速为80cm/s ，则小动脉此处的内径应为〔〕mm 。

A ．4B ．3C ．2D ．18、正常情况下，人的血液密度为1.05×103kg/m 3，血液在内径为6mm 的小动脉中流动的平均速度为20cm/s ，若小动脉某处被一硬斑阻塞而变窄，此处内径为4mm ，则小动脉宽处与窄处压强之差〔〕Pa 。

第1章 绪论1.1 若某种牌号的汽油的重度γ为7000N/m 3，求它的密度ρ。

解：由g γρ=得，3327000N/m 714.29kg/m 9.8m /m γρ===g1.2 已知水的密度ρ=997.0kg/m 3，运动黏度ν=0.893×10-6m 2/s ，求它的动力黏度μ。

解：ρμ=v 得，3624997.0kg/m 0.89310m /s 8.910Pa s μρν--==⨯⨯=⨯⋅ 1.3 一块可动平板与另一块不动平板同时浸在某种液体中，它们之间的距离为0.5mm ，可动板若以 0.25m/s 的速度移动，为了维持这个速度需要单位面积上的作用力为2N/m 2，求这两块平板间流体的动力黏度μ。

解：假设板间流体中的速度分布是线性的，则板间流体的速度梯度可计算为13du u 0.25500s dy y 0.510--===⨯ 由牛顿切应力定律d d uyτμ=，可得两块平板间流体的动力黏度为 3d 410Pa s d yuτμ-==⨯⋅1.4上下两个平行的圆盘，直径均为d ，间隙厚度为δ，间隙中的液体动力黏度系数为μ，若下盘固定不动，上盘以角速度ω旋转，求所需力矩T 的表达式。

题1.4图解：圆盘不同半径处线速度 不同，速度梯度不同，摩擦力也不同，但在微小面积上可视为常量。

在半径r 处，取增量dr ，微面积 ，则微面积dA 上的摩擦力dF 为du r dF dA2r dr dz ωμπμδ== 由dF 可求dA 上的摩擦矩dT32dT rdF r dr πμωδ==积分上式则有d 43202d T dT r dr 32πμωπμωδδ===⎰⎰1.5 如下图所示，水流在平板上运动，靠近板壁附近的流速呈抛物线形分布，E 点为抛物线端点，E 点处0d =y u ，水的运动黏度ν=1.0×10-6m 2/s ，试求y =0，2，4cm 处的切应力。

（提示：先设流速分布C By Ay u ++=2，利用给定的条件确定待定常数A 、B 、C ）题1.5图解：以D 点为原点建立坐标系，设流速分布C By Ay u ++=2，由已知条件得C=0,A=-625,B=50则2u 625y 50y =-+ 由切应力公式du dy τμ=得du(1250y 50)dyτμρν==-+ y=0cm 时，221510N /m τ-=⨯；y=2cm 时，222 2.510N /m τ-=⨯；y=4cm 时，30τ= 1.6 某流体在圆筒形容器中。

第3章 流体动力学基础3.1 解： zuu y u u x u u t u a x z x y x x x x ∂∂+∂∂+∂∂+∂∂=()()342246222222222=++++=+-++++=++=z y x t z y t y x t u u y xzu u yu u xu u tu a y zy yy xy y ∂∂+∂∂+∂∂+∂∂=()()32111=-++=-+++--=+-=z y x z x t z y t u u x yzu u y u u x u u t u a z z z y z x z z ∂∂+∂∂+∂∂+∂∂=()()112122211=++++=-+-+++=-+=z y x t z y t y x t u u z x222286.35s m a a a a z y x =++=3.2 解：（1）3235623=-=+=xy xy u xy y u a y x x222527310.3333231s m a a a y u y a y x y y =+===-=（2）二元流动（3）恒定流 （4）非均匀流 3.3 解：bh u y h u bdy h y u udA Q h hA m ax 07871m ax 071m ax 8787==⎪⎭⎫ ⎝⎛==⎰⎰ m ax 87u A Q v ==3.4 解：s m dd v v 02.011.02221221=⎪⎭⎫ ⎝⎛⨯=⎪⎪⎭⎫ ⎝⎛= 3.5 解：Hd v d 1v 1q 1q 2223d 3v Dv 1dv 2（1）s m v d Q 332330785.04==πs m q Q Q 32321.0=+= s m Q q Q 321115.0=+=（2）s m d Q v 12.242111==πs m d Q v 18.342222==π 3.6 解：渠中：s m m m s m bh v Q 311612/3=⨯⨯==管中：2231242.1d v s m Q Q Q ⨯⨯==-=πm v Q d 0186.1422==π 3.7 解： s m d d v v ABB A62.04.05.1442222=⨯=⋅=ππ以过A 点的水平面为等压面，则OmH g v g p h H OmH g v g p H B B B A A A 2222226964.58.925.18.9405.128980.48.9268.9302=⨯++=++==⨯+=+=ρρ可以看出：A B H H >，水将从B 点流向A 点。

第一章：绪论例1-1 200 ºC体积为的2.5m3水，当温度升至800ºC时，其体积增加多少？解： 200 ºC时：ρ1=998.23kg/m3 800CºC时：ρ2=971.83kg/m3即：则：例1-2使水的体积减小0.1%及1%时，应增大压强各为多少？（K=2000MPa）d V/V =-0.1%=-2000×106×（-0.1%）=2×106Pa=2.0MPad V /V = -1%= -2000×106×（-1%）=20 MPa例1-3输水管l=200m，直径d=400mm，作水压试验。

使管中压强达到55at后停止加压，经历1小时，管中压强降到50at。

如不计管道变形，问在上述情况下，经管道漏缝流出的水量平均每秒是多少？水的体积压缩率κ =4.83×10-10m2 /N 。

解水经管道漏缝泄出后，管中压强下降，于是水体膨胀，其膨胀的水体积水体膨胀量5.95 l 即为经管道漏缝流出的水量，这是在1小时内流出的。

设经管道漏缝平均每秒流出的水体积以Q 表示，则例1-4：试绘制平板间液体的流速分布图与切应力分布图。

设平板间的液体流动为层流，且流速按直线分布，如图1-3所示。

解：设液层分界面上的流速为u,则：切应力分布：图1-3上层下层：在液层分界面上：--流速分布：上层：下层：例1-5：一底面积为40 ×45cm2，高为1cm的木块，质量为5kg，沿着涂有润滑油的斜面向下作等速运动，如图1-4所示，已知木块运动速度u =1m/s，油层厚度d =1mm，由木块所带动的油层的运动速度呈直线分布，求油的粘度。

解：∵等速∴αs =0由牛顿定律：∑F s=mαs=0m gsinθ－τ·A=0（呈直线分布）图1-4∵ θ=tan-1(5/12)=22.62°例1-6: 直径10cm的圆盘，由轴带动在一平台上旋转，圆盘与平台间充有厚度δ=1.5mm的油膜相隔，当圆盘以n =50r/min旋转时，测得扭矩M =2.94×10-4 N·m。

第三、四章 流体动力学基础习题及答案3-8已知流速场u x =xy 2, 313y u y =-, u z =xy, 试求：（1）点（1，2，3）的加速度；（2）是几维流动；（3）是恒定流还是非恒定流；（4）是均匀流还是非均匀流？解：（1）411633x x x x x x y z u u u u a u u u xy t x y z ∂∂∂∂=+++==∂∂∂∂25333213313233312163. 06m/s y y z x y a y u y a yu xu xy xy xy a =-===+=-====（2）二元流动 （3）恒定流（4）非均匀流41xy 33-11已知平面流动速度分布为x y 2222cxu u x ycy x y =-=++，， 其中c 为常数。

求流线方程并画出若干条流线。

解：2222-xdx=ydyx ydx dydx dy cy cx u u x y x y =⇒-=⇒++积分得流线方程：x 2+y 2=c方向由流场中的u x 、u y 确定——逆时针3-17下列两个流动，哪个有旋？哪个无旋？哪个有角变形？哪个无角变形？(1)u x =－ay,u y =ax,u z =0 （2）z 2222,,0,a c x ycy cxu u u x y x y =-==++式中的、为常数。

z 2222,,0,a c x y cy cxu u u x y x y =-==++式中的、为常数。

解：（1）110 ()()22yx x y z u u a a a xy ωωω∂∂===-=+=∂∂有旋流动 xy 11()()0 22y x xy zx u u a a x y εεε∂∂=+=-==∂∂ 无角变形 (2)222222222222222222211()2()2()22()()12()2()0 0 2()y x z x y u u x y c cx x y c cy x y x y x y c x y c x y x y ωωω∂⎡⎤∂+-+-=-=+⎢⎥∂∂++⎣⎦⎡⎤+-+====⎢⎥+⎣⎦无旋流动2222xy 22222112()()()022()()y x u u c x y c x y x y x y x y ε∂⎡⎤∂---=+==-≠⎢⎥∂∂++⎣⎦ 有角变形4—7变直径管段AB ，d A =0.2m,d B =0.4m ，高差△h=1.5m ，测得p A =30kPa ，p B =40kPa ，B 点处断面平均流速v B =1.5m/s ，试判断水在管中的流动方向。

第三章流体动力学基础一、复习思考题二、习题1、选择题2、计算题一、复习思考题1．比较拉格朗日法和欧拉法，两种方法及其数学表达式有何不同？2．什么是流线？流线有哪些重要性质，流线和迹线有无重合的情况？3．总流连续性方程的物理意义是什么？4．何谓均匀流及非均匀流？以上分类与过流断面上流速分布是否均匀有无关系？5．何谓渐变流，渐变哪些有哪些重要性质？引入渐变流概念，对研究流体运动有什么实际意义？6．动能校正系数及动量校正系数的物理意义是什么？7．说明总流伯努力利方程各项的物理意义和几何意义。

8．应用总流伯努力利方程解题时，在所取过流断面上，不同点单位重量液体具有的机械能是否相等？9．结合公式的推导，说明总流伯努力利方程的适用条件。

10．结合公式推导，说明总流动量方程适用条件。

二、习题1、选择题3-1 恒定流是：（a）流动随时间按一定规律变化；（b）流场中任意空间点的运动要素不随时间变化；（c）各过流断面的流速分布不同；（d）各过流断面的压强相同。

3-2 非恒定流是：（a）əu/ət=0；（b）əu/ət≠0；（c）əu/əS=0；（d）əu/əS≠0。

3-3 一元运动是：（a）均匀流；（b）速度分布按直线变化；（c）运动参数是一个空间坐标和时间变量的函数；（d）限于直线运动。

3-4 均匀流是：（a）当地加速度为零；（b）迁移加速度为零；（c）向心加速度为零；（d）合加速度为零。

3-5 变直径管的直径d1=320mm，d2=160mm，流速v1=1.5m/s，v2为：（a）3 m/s；（b）4 m/s；（c）6m/s；（d）9 m/s。

3-6 一等直径水管，A-A为过流断面，B-B为水平面，1、2、3、4为面上各点，各点的运动物理量有以下关系：（a）p1=p2；（b）p3= p4；（c）z1+（p1/ρg）= z2+（p2/ρg）；（d）z3+（p3/ρg）= z4+（p4/ρg）。

3-7 伯努利方程中z+（p/ρg）+（αv2/2g）表示：（a）单位重量流体具有的机械能；（b）单位质量流体具有的机械能；（c）单位体积流体具有的机械能；（d）通过过流断面流体的总机械能。

第三章流体运动学与动力学基础主要内容●基本概念●欧拉运动微分方程●连续性方程——质量守恒*●伯努利方程——能量守恒** 重点●动量方程——动量守恒** 难点●方程的应用第一节研究流体运动的两种方法●流体质点：物理点。

是构成连续介质的流体的基本单位，宏观上无穷小（体积非常微小，其几何尺寸可忽略），微观上无穷大（包含许许多多的流体分子，体现了许多流体分子的统计学特性）。

●空间点：几何点，表示空间位置。

流体质点是流体的组成部分，在运动时，一个质点在某一瞬时占据一定的空间点（x，y，z）上，具有一定的速度、压力、密度、温度等标志其状态的运动参数。

拉格朗日法以流体质点为研究对象，而欧拉法以空间点为研究对象。

一、拉格朗日法（跟踪法、质点法）Lagrangian method1、定义：以运动着的流体质点为研究对象，跟踪观察个别流体质点在不同时间其位置、流速和压力的变化规律，然后把足够的流体质点综合起来获得整个流场的运动规律。

2、拉格朗日变数：取t=t0时，以每个质点的空间坐标位置为（a，b，c）作为区别该质点的标识，称为拉格朗日变数。

3、方程：设任意时刻t，质点坐标为(x，y，z) ，则：x = x(a,b,c,t)y = y(a,b,c,t)z = z(a,b,c,t)4、适用情况：流体的振动和波动问题。

5、优点：可以描述各个质点在不同时间参量变化，研究流体运动轨迹上各流动参量的变化。

缺点：不便于研究整个流场的特性。

二、欧拉法（站岗法、流场法）Eulerian method1、定义：以流场内的空间点为研究对象，研究质点经过空间点时运动参数随时间的变化规律，把足够多的空间点综合起来得出整个流场的运动规律。

2、欧拉变数：空间坐标（x，y，z）称为欧拉变数。

3、方程：因为欧拉法是描写流场内不同位置的质点的流动参量随时间的变化，则流动参量应是空间坐标和时间的函数。

位置：x = x(x,y,z,t)y = y(x,y,z,t)z = z(x,y,z,t)速度：u x=u x（x,y,z,t）u y=u y（x,y,z,t）u z=u z（x,y,z,t）同理：p=p（x,y,z,t），ρ=ρ(x,y,z,t)说明： x 、y 、z 也是时间t 的函数。

第一章：绪论例1-1 200 ºC体积为的2.5m3水，当温度升至800ºC时，其体积增加多少？解： 200 ºC时：ρ1=998.23kg/m3 800CºC时：ρ2=971.83kg/m3即：则：例1-2使水的体积减小0.1%及1%时，应增大压强各为多少？（K=2000MPa）d V/V =-0.1%=-2000×106×（-0.1%）=2×106Pa=2.0MPad V /V = -1%= -2000×106×（-1%）=20 MPa例1-3输水管l=200m，直径d=400mm，作水压试验。

使管中压强达到55at后停止加压，经历1小时，管中压强降到50at。

如不计管道变形，问在上述情况下，经管道漏缝流出的水量平均每秒是多少？水的体积压缩率κ =4.83×10-10m2 /N 。

解水经管道漏缝泄出后，管中压强下降，于是水体膨胀，其膨胀的水体积水体膨胀量5.95 l 即为经管道漏缝流出的水量，这是在1小时内流出的。

设经管道漏缝平均每秒流出的水体积以Q 表示，则例1-4：试绘制平板间液体的流速分布图与切应力分布图。

设平板间的液体流动为层流，且流速按直线分布，如图1-3所示。

解：设液层分界面上的流速为u,则：切应力分布：图1-3上层下层：在液层分界面上：--流速分布：上层：下层：例1-5：一底面积为40 ×45cm2，高为1cm的木块，质量为5kg，沿着涂有润滑油的斜面向下作等速运动，如图1-4所示，已知木块运动速度u =1m/s，油层厚度d =1mm，由木块所带动的油层的运动速度呈直线分布，求油的粘度。

解：∵等速∴αs =0由牛顿定律：∑F s=mαs=0m gsinθ－τ·A=0（呈直线分布）图1-4∵ θ=tan-1(5/12)=22.62°例1-6: 直径10cm的圆盘，由轴带动在一平台上旋转，圆盘与平台间充有厚度δ=1.5mm的油膜相隔，当圆盘以n =50r/min旋转时，测得扭矩M =2.94×10-4 N·m。

第三章 流体运动学及动力学基础练习题一、 单项选择题1. 定常流动中，流体质点的加速度等于（ ）A ．等于零 B. 等于常量 C 随时间变化而变化 D 与时间无关2. 一维流动的连续性方程C VA =成立的必要条件是（ ）A 理想流体B 黏性流体C 可压缩流体D 不可压缩流体3. 均匀流是（ ）A 当地加速度为零B 迁移加速度为零C 向心加速度为零D 合加速度为零4. 均匀流过流断面上各点的（ ）等于常数A. PB. g p z ρ+C. g V g p 22+ρ D gV g p z 22++ρ 5. 用欧拉法研究流体运动时，流体质点的加速度a=( )A. 22dtr d B. t ∂∂U C )u u.∇( D )u u.U ∇+∂∂(t 6. 控制体是指相对于某个坐标系来说（ ）A 由确定的流体质点所组成的流体团B 有流体流过的固定不变的任何体积C 其形状、位置随时间变化的任何体积D 其形状不变而位置随时间变化的任何体积7. 恒定总流的连续方程、伯努利方程、动量方程中的流速为（ ）A 断面平均流速B 断面上的最大流速C 断面形心处的流速D 断面上压力中心处的流速8. 关于水流流向的正确说法是（ ）A 水一定是从高处往低处流B 水一定是从流速大处往流速小处流C 水一定是从机械能大处往机械能小处流D 水一定是从测压管水头高处往测压管水头低处流9. 非恒定流动中，流线与迹线( )A 一定重合B 一定不重合C 特殊情况下可能重合D 一定正交10. 在应用恒定总流的动量方程∑-=)(1122v v q F v ββρ解体时，∑F 中不应该包括（ ）A 重力B 压力C 阻力D 惯性力二 、思考题1. “均匀流和渐变流必为恒定流，急变流必为非恒定流”，这种说法对否？为什么？2. 在河道中，为什么自由航行的船只总是向水流较急的一侧河岸靠拢？三．计算题1.2.3.4.。