pai定理 工程流体力学例题
- 格式:docx
- 大小:152.53 KB
- 文档页数:4

《工程流体力学》习题(一)第一章 流体的物理性质【1-1】500cm 3的某种液体,在天平上称得其质量为0.453kg ,试求其密度和相对密度。
【解】3340.4530.90610 kg/m 510m Vρ-===⨯⨯330.906100.9061.010w ρδρ⨯===⨯【1-2】 体积为5m 3的水,在温度不变的条件下,当压强从98000Pa 增加到4.9×105Pa 时,体积减少1升。
求水的压缩系数和弹性系数。
【解】由压缩系数公式10510.0015.110 1/Pa 5(4.91098000)p dV V dPβ-=-==⨯⨯⨯-911 1.9610 Pa 5.1pE β===⨯【1-3】温度为20℃,流量为60 m 3/h 的水流入加热器,如果水的体积膨胀系数βt =0.00055K -1,问加热到80℃后从加热器中流出时的体积流量变为多少?【解】根据膨胀系数1t dV V dtβ=则211t Q Q dt Q β=+3600.00055(8020)6061.98 m /h =⨯⨯-+=【1-4】图中表示浮在油面上的平板,其水平运动速度为u =1m/s ,δ=10mm ,油品的粘度μ=0.9807Pa·s ,求作用在平板单位面积上的阻力。
【解】根据牛顿内摩擦定律习题1-4图=du dyτμ则21=0.980798.07N/m 0.01τ⨯=【1-5】已知半径为R 圆管中的流速分布为22=(1)ru c R-式中c 为常数。
试求管中的切应力τ与r 的关系。
【解】根据牛顿内摩擦定律=du dyτμ则2222=[(1)]d r r c c dr RR τμμ-=-第二章 流体静力学【2-1】容器中装有水和空气,求A 、B 、C 和D 各点的表压力?【解】34342223232()()()(2)MA MB MA MC MB MD MC p g h h p p g h h h gh p p gh p p g h h g h h ρρρρρρ=+=-++=-==-=-+=-+【2-2】如图所示的U 形管中装有水银与水,试求:(1)A 、C 两点的绝对压力及表压力各为多少? (2)求A 、B 两点的高度差h ? 【解】(1) ()w 0.3ab A a p p g ρ=+⨯w 0.3MA p g ρ=⨯习题1-5图题2-1图1题2-2图B()w H 0.30.1ab C a p p g g ρρ=+⨯+⨯w H 0.30.1MC p g g ρρ=⨯+⨯(2)选取U 形管中水银的最低液面为等压面,则w H 0.3g gh ρρ⨯=得 w H0.322 c m h ρρ⨯==【2-3】 在一密闭容器内装有水及油,密度分别为ρw 及ρo ,油层高度为h 1,容器底部装有水银液柱压力计,读数为R ,水银面与液面的高度差为h 2,试导出容器上方空间的压力p 与读数R 的关系式。

伯努利例题解析伯努利定理是流体力学中非常重要的一个定理,描述了在无粘不可压缩流体中,速度增加导致压力降低的现象。
伯努利定理可以用以下等式进行表达:P + 1/2ρv^2 + ρgh = 常数其中,P表示流体的压力,ρ表示流体的密度,v表示流体的速度,g表示重力加速度,h表示流体的高度。
现在我们来看一个例题并进行解析。
例题:水平地面上有一管道,管道中的水流速度为2 m/s,管道的截面积为0.01 m^2,管道上部为水平,下部垂直向下,下部的直径为管道截面的一半。
求上部和下部的压力差。
解析:首先,我们可以利用伯努利定理来解答这个问题。
由于问题中的流体为水,我们可以将△表示为ρg△h,其中ρ为水的密度,g为重力加速度,△h为水的高度差。
根据伯努利定理,我们可以写出上部和下部的压力差为:(P上+ 1/2ρv上^2 + ρgh上) - (P下+ 1/2ρv下^2 + ρgh下) = 0由于上部为水平,所以△h上为0,且根据管道的连续性方程,我们可以得到v上 = v下/2。
将这些代入上述方程中,我们可以得到:( P上+ 1/2ρ(v下/2)^2 ) - ( P下 + 1/2ρv下^2 + ρgh下) = 0化简得: P上 - P下= 1/2ρ(v下^2/4 - v下^2) - ρgh下进一步化简得: P上 - P下 = - 1/8ρv下^2 - ρgh下现在我们已经得到了上部和下部的压力差的表达式,接下来我们带入具体的数值进行计算。
假设水的密度ρ为1000 kg/m^3,重力加速度g为9.8 m/s^2,则有:P上 - P下 = - 1/8(1000)(2^2) - (1000)(9.8)(0.01/2)化简得: P上 - P下 = - 10 - 0.49 = -10.49 Pa所以上部和下部的压力差为10.49 Pa,并且由于下部的压力更大,所以下部的压力比上部的压力高10.49 Pa。
这道题目的关键在于利用伯努利定理并对方程进行一系列的化简,从而得到上部和下部压力差的表达式。

第六章 量纲分析和相似原理答案6-1由实验观测得知,如图6-1所示的三角形薄壁堰的流量Q 与堰上水头H 、重力加速度g 、堰口角度θ以及反映水舌收缩和堰口阻力情况等的流量系数m 0(量纲一的量)有关。
试用π定理导出三角形堰的流量公式。
解:()00θ=,,,,f Q H g m选几何学的量H ,运动学的量g 作为相互独立的物理量,有3个π项。
111πa H g Q β=,222a H g,3330πa H g m对1π,其量纲公式为11000-23-1L T M =L (LT )L T11L :03αβ=++,1T :021β=--解出152α=-,112β=-,则可得 152πQg H对2π,其量纲公式为220002L T M L (LT )22L :0αβ=+,2T :02β=-联立解上述方程组,可得02=α,02=β,02=γ,则可得2π对3π,其量纲公式为33000-2L T M L (LT )33L :0αβ=+,3T :02β=-联立解上述方程组,可得03=α,03=β,03=γ,则可得30πm123πππ0F ,,即052()0Q F m ,,或1052()Q F m ,2501),(H g m F Q θ=式中,θ要视堰口的实际角度而定,量纲一的量0m 要由实验来确定。
第十章三角形薄壁堰的理论分析解5204tan 252Qm gh 与上式形状相同。
6-2 根据观察、实验与理论分析,认为总流边界单位面积上的切应力τ0,与流体的密度ρ、动力粘度μ、断面平均流速v ,断面特性几何尺寸(例如管径d 、水力半径R )及壁面粗糙凸出高度Δ有关。
试用瑞利法求τ0的表示式; 若令沿程阻力系数8(,)λ∆=f Re d,可得208λτρ=v 。
解:351240τkv d将上式写成量纲方程形式后得35124-1-23-1-110dim ML T =(ML )(ML T )(LT )(L)(L)ααααατ--=根据量纲和谐原理可得:12M :1αα=+12345L :13ααααα-=--+++ 23T :2αα-=--选53αα、为参变量,联立解上述方程组可得:131αα=-,232αα=-,4352ααα=-+-。



流体力学答案解析题目:一不可压缩流体在水平管道内作稳定流动,管道截面由圆形逐渐扩大为方形,入口直径为d,出口边长为a。
已知入口流速为v1,入口处的压力为p1,求出口处的流速v2和压力p2。
解析:首先,根据连续性方程,流体在管道内的流速和截面积之间存在以下关系:A1v1 = A2v2其中,A1和A2分别为入口和出口的截面积。
由于管道截面由圆形变为方形,我们可以分别计算两个截面的面积。
入口截面积A1 = π(d/2)^2出口截面积 A2 = a^2将上述面积代入连续性方程,得到:π(d/2)^2 v1 = a^2 v2解得:v2 = (π(d/2)^2 v1) / a^2接下来,我们应用伯努利方程,该方程描述了流体在流动过程中速度、压力和高度之间的关系。
在水平管道中,高度不变,因此伯努利方程简化为:p1/ρ + v1^2/2 = p2/ρ + v2^2/2其中,ρ为流体的密度。
将v2的表达式代入伯努利方程,得到:p1/ρ + v1^2/2 = p2/ρ + (π(d/2)^2 v1)^2 /(2a^2ρ)化简得到:p2 = p1 + ρ(v1^2 - v2^2)/2将v2的表达式代入上式,得到:p2 = p1 + ρ(v1^2 - (π(d/2)^2 v1)^2 /(2a^2ρ))/2化简得到:p2 = p1 + (ρ/2)(v1^2 - (π(d/2)^4 v1^2) / (2a^2))进一步化简得到:p2 = p1 + (ρ/2)(v1^2(1 - (π(d/2)^4) / (2a^2)))至此,我们已经求得了出口处的流速v2和压力p2。
以下是对解题过程的详细解析:1. 连续性方程的应用:连续性方程是流体力学中的一个基本原理,描述了流体在流动过程中质量守恒的关系。
在本题中,由于流体是不可压缩的,因此在流动过程中质量守恒。
根据连续性方程,我们可以求出出口处的流速v2。
2. 伯努利方程的应用:伯努利方程是流体力学中的一个重要方程,描述了流体在流动过程中速度、压力和高度之间的关系。



工程流体力学习题及答案工程流体力学习题及答案工程流体力学是研究流体在工程领域中的运动规律和力学性质的学科。
它在各个工程领域中都有广泛的应用,例如水力工程、航空航天工程、石油工程等。
在学习工程流体力学的过程中,解决习题是提高理论应用能力的重要途径。
下面,我们将介绍一些常见的工程流体力学习题及其详细解答。
1. 一个长方形截面的水槽,长为2m,宽为1m,高为1.5m。
槽中注满了水,求水的质量。
解答:水的质量可以通过体积和密度的乘积来计算。
首先计算水的体积,即长方体的体积,公式为V = 长× 宽× 高= 2m × 1m × 1.5m = 3m³。
然后,根据水的密度为1000kg/m³,将体积乘以密度,即可得到水的质量。
所以,水的质量为3m³ × 1000kg/m³ = 3000kg。
2. 一个圆柱形容器,半径为0.5m,高度为2m,容器中注满了油,油的密度为900kg/m³。
求油的质量。
解答:油的质量可以通过体积和密度的乘积来计算。
首先计算油的体积,即圆柱体的体积,公式为V = π × 半径² × 高度= 3.14 × (0.5m)² × 2m = 1.57m³。
然后,根据油的密度为900kg/m³,将体积乘以密度,即可得到油的质量。
所以,油的质量为1.57m³ × 900kg/m³ = 1413kg。
3. 一根半径为0.1m的水管,水流速度为2m/s,求水管中的水流量。
解答:水流量可以通过流速和管道截面积的乘积来计算。
首先计算管道的截面积,即圆的面积,公式为A = π × 半径² = 3.14 × (0.1m)² = 0.0314m²。
然后,将流速乘以截面积,即可得到水流量。

工程流体力学第一章思索题1、为什么要引进连续介质的假设?为什么可以把液体当作连续介质?2、非均质液体的密度应当如何表示?3、流体粘度与哪些因素有关?它们随温度是如何变化的?对流体有何影响?4、为什么水通常被视为不行压缩流体?什么状况下要考虑液体的可压缩性和表面张力特性?5、液体内摩擦力的大小与哪些因素有关?牛顿内摩擦定律的适用条件有哪些?6、图为管道过水断面水流流速分布图,从其对应部位取出水体A,试标出水体A顶面和底面切应力的方向。
思索题6图7、为什么要引入抱负液体的概念?它与实际液体有什么区分?8、单位质量力怎样定义的?静止液体和作自由落体运动的液体所受的单位质量力分别为多少?习题1.1容器中盛有静止液体,此时液体所受到的单位质量力为多少?1.2假设水的体积弹性系数犬=2.2、1()6长修,欲使其体积减小0.4乐问需要增加多大的压强?1.3当压强的增量为5OKN∕7∕,某种液体的密度增长0. 02%,试求该液体的体积模量。
1. 4平板面积为50x50。
/,厚度为1. 0cm,质量m=5kg,沿着涂有厚度5=1. 0mm油的斜面对下作等速运动,其速度尸 1. Om∕s,带动油层的运动速度呈直线分布,油的密度P =950 kg∕m3,求油的动力粘度和运动粘度。
1.5 某种液体布满两平行边界的缝隙5内,液体的动力粘度为为",有一面积为力的极薄的平板以 速度u 平行于平板移动。
x 为平板距上边界的距离。
求:平板所受的拖力T,(缝隙内的流速按直1.6 水流在平板上运动(如第6题图),流速分布曲线DE 为抛物线形,E 点为抛物线端点,E 点处 也=0dy ~ ,水的运动粘度v = 1.0xl02m2∕s,试求y = 0,2,4cm 处的切应力(提示:先设流速分布 u = Ay 2+By + C,采用给出的条件确定待定常数A, B, C )o 其次章思索题1、抱负流体处于静止状态时受到哪儿种力的作用?2、等压面应具备什么条件?在什么条件下“静止液体内任何一个水平面都是等压面”的说法是正确的?3、下列哪一些是正确的等压面?油水 t=∏ I 水-D思索题3图4、水静力学基本方程的形式和表示的物理意义是什么?5、压力表和测压计测得的压强是肯定压强还是相对压强?6、静止液体、流淌液体中,各点的测压管水头是否相等?线分布)。
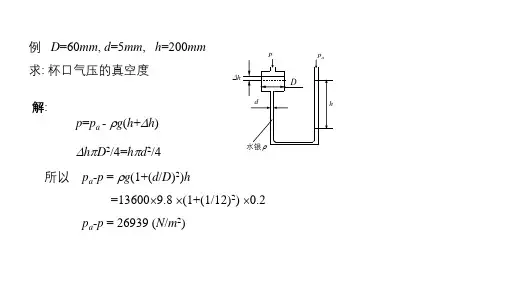
典 型 例 题 1 基本概念及方程【1-1】底面积A =0.2m ×0.2m 的水容器,水面上有一块无重密封盖板,板上面放置一个重量为G 1=3000N 的铁块,测得水深h =0.5m ,如图所示。
如果将铁块加重为G 2=8000N ,试求盖板下降的高度Δh 。
【解】:利用体积弹性系数计算体积压缩率:E p v v //∆=∆ )/(00B p p np E +=p 为绝对压强。
当地大气压未知,用标准大气压Pa p 501001325.1⨯=代替。
Pa A G p p 51011076325.1/⨯=+=Pa A G p p 52021001325.3/⨯=+=因 01/p p 和 02/p p 不是很大,可选用其中任何一个,例如,选用02/p p 来计算体积弹性系数:Pa B p p np E 9020101299.2)/(⨯=+=在工程实际中,当压强不太高时,可取 Pa E 9101.2⨯=512104827.6/)(///-⨯=-=∆=∆=∆E p p E p v v h hm h h 55102413.310604827--⨯=⨯=∆【2-2】用如图所示的气压式液面计测量封闭油箱中液面高程h 。
打开阀门1,调整压缩空气的压强,使气泡开始在油箱中逸出,记下U 形水银压差计的读数Δh 1=150mm ,然后关闭阀门1,打开阀门2,同样操作,测得Δh 2=210mm 。
已知a =1m ,求深度h 及油的密度ρ。
【解】水银密度记为ρ1。
打开阀门1时,设压缩空气压强为p 1,考虑水银压差计两边液面的压差,以及油箱液面和排气口的压差,有同样,打开阀门2时,两式相减并化简得代入已知数据,得所以有2 基本概念及参数【1-3】测压管用玻璃管制成。
水的表面张力系数σ=0.0728N/m ,接触角θ=8º,如果要求毛细水柱高度不超过5mm ,玻璃管的内径应为多少? 【解】由于因此【1-4】高速水流的压强很低,水容易汽化成气泡,对水工建筑物产生气蚀。
工程流体力学习题及答案(1)1 某种液体的比重为3,试求其比容。
(答:3.3×10-4米3/公斤)2 体积为5.26米3的某种油,质量为4480公斤,试求这种油的比重、密度与重度。
(答:0.85;851公斤/米3;8348牛/米3)3 若煤油的密度为0.8克/厘米3,试求按工程单位计算的煤油的重度、密度与比容。
(答:800公斤力/米3;81.56公斤力·秒2/米4;1.25×10-3米3/公斤力)4 试计算空气在温度t=4℃,绝对压力P=3.4大气压下的重度、密度与比容。
(答:42.4牛/米3;4.33公斤/米3;0.231米3/公斤)5 试计算二氧化碳在温度为t=85℃,绝对压力P=7.1大气压下的重度、密度与比容。
(答:104牛/米3;10.6公斤/米3;0.09厘米3/公斤 )6 空气在蓄热室内于定压下,温度自20℃增高为400℃,问空气的体积增加了多少倍? (答:1.3倍)7 加热炉烟道入口烟气的温度900=t 入℃,烟气经烟道及其中设置的换热器后,至烟道出口温度下降为500=t 出℃,若烟气在0℃时的密度为28.10=ρ公斤/米3,求烟道入口与出口处烟气的密度。
(答:298.0=ρ人公斤/米3;452.0=ρ出公斤/米3) 8 试计算一氧化碳在表压力为0.3大气压、温度为8℃下的重度。
(答:15.49牛/米3)9 已知速度为抛物线分布,如图示 y=0,4,8,12,17厘米处的速度梯度。
又若气体的绝对粘性系数为1013.25-⨯=μ牛·秒/米3,求以上各处气体的摩擦切应力。
9 题图10 夹缝宽度为h ,其中所放的很薄的大平板以定速v 移动。
若板上方流体的粘性系数为μ,下方流体的粘性系数为K μ,问应将大平板放在夹缝中何处,方能使其移动时阻力为最小?(答:h kk kh =++11或)11 如图所示,一正方形b ×b=67×67厘米2、质量为12公斤的平板,在厚3.1=δ毫米的油膜支承下,以匀速v=0.18米/秒沿一斜面滑下,问油的粘性系数是多少?10 题图 11 题图(答:0.728牛·秒/米2)12 如图所示,气缸直径D 1=16厘米,活塞直径D 2=16厘米,质量0.97公斤,若活塞以匀速0.05米/秒在气缺内下降,试求油的粘性系数是多少?12 题图 15 题图(答:0.63牛·秒/米2)13 直径为150毫米的圆柱,固定不动。
π定理例题讲解一、π定理基本概念1. 量纲分析- 量纲是物理量的基本属性。
在力学中,基本量纲通常取为长度L、质量M 和时间T。
例如,速度的量纲为[v]=LT^-1,力的量纲为[F]=MLT^-2。
2. π定理内容- 设某一物理过程涉及n个物理量x_1,x_2,·s,x_n,这些物理量之间存在函数关系f(x_1,x_2,·s,x_n) = 0。
若在这n个物理量中有m个基本量(例如在力学中m = 3,基本量为长度、质量、时间),则可组成n - m个无量纲量π_1,π_2,·s,π_n - m,且存在函数关系F(π_1,π_2,·s,π_n - m)=0。
二、例题讲解1. 例题- 已知单摆的摆动周期T与摆长l、重力加速度g和摆球质量m有关,试用量纲分析的π定理求周期T的表达式。
2. 解析步骤- (1)确定相关物理量及其量纲- 已知物理量有T(时间,量纲[T]=T)、l(长度,量纲[l]=L)、g(重力加速度,量纲[g]=LT^-2)、m(质量,量纲[m]=M),这里n = 4个物理量。
- 在力学中基本量有长度L、质量M、时间T,所以m = 3。
- (2)选择基本量- 我们选择l(长度)、m(质量)、g(重力加速度)作为基本量。
- (3)构造无量纲量π- 设π = T^a l^b m^c g^d,根据量纲齐次性原理,对于量纲L:0 = b + d;对于量纲M:0=c;对于量纲T:0 = a- 2d。
- 由c = 0,b=-d,a = 2d,令d = - (1)/(2),则a = 1,b=(1)/(2)。
- 所以π=(T√(g))/(√(l)),根据π定理,F(π)=0,这里F为某个函数,由于π是无量纲量,实际上π = C(C为常数)。
- 所以T = C√(frac{l){g}},这就是单摆周期的表达式(其中C = 2π可以通过理论推导或者实验确定)。
《流体力学》典型例题(9大类)例1~例3——牛顿内摩擦定律(牛顿剪切公式)应用例4~例5——流体静力学基本方程式的应用——用流体静力学基本方程和等压面计算某点的压强或两点之间的压差。
例6~例8——液体的相对平衡——流体平衡微分方程中的质量力同时考虑重力和惯性力(补充内容) (1)等加速直线运动容器中液体的相对平衡(与坐标系选取有关) (2)等角速度旋转容器中液体的平衡(与坐标系选取有关)例9——求流线、迹线方程;速度的随体导数(欧拉法中的加速度);涡量计算及流动有旋、无旋判断 例10~16——速度势函数、流函数、速度场之间的互求 例17——计算流体微团的线变形率、角变形率及旋转角速度 例18~20——动量定理应用(课件中求弯管受力的例子) 例21~22——总流伯努利方程的应用例23——综合:总流伯努利方程、真空度概念、平均流速概念、流态判断、管路系统沿程与局部损失计算例题1:如图所示,质量为m =5 kg 、底面积为S =40 cm ×60 cm 的矩形平板,以U =1 m/s 的速度沿着与水平面成倾角θ=30的斜面作等速下滑运动。
已知平板与斜面之间的油层厚度δ=1 mm ,假设由平板所带动的油层的运动速度呈线性分布。
求油的动力粘性系数。
UG=mgθ解:由牛顿内摩擦定律,平板所受的剪切应力du U dy τμμδ==又因等速运动,惯性力为零。
根据牛顿第二定律:0m ==∑F a ,即:gsin 0m S θτ-⋅=()324gsin 59.8sin 301100.1021N s m 1406010m U S θδμ--⋅⨯⨯⨯⨯==≈⋅⋅⨯⨯⨯粘性是流体在运动状态下,具有的抵抗产生剪切变形速率能力的量度;粘性是流体的一种固有物理属性;流体的粘性具有传递运动和阻滞运动的双重性。
例题2:如图所示,转轴的直径d =0.36 m ,轴承的长度l =1 m ,轴与轴承的缝隙宽度δ=0.23 mm ,缝隙中充满动力粘性系数0.73Pa s μ=⋅的油,若轴的转速200rpm n =。
帕斯卡定律、连通器、气体、流体压强专题训练训练一:1.连通器在日常生活、生产中有着广泛的应用。
图中所示的事例中利用连通器原理的是()A .只有(1)(2)B .只有(3)(4)C .只有(1)(3)(4)D .(1)(2)(3(4)2.密闭的液体有一个重要的特点,即加在密闭液体上的压强,能够大小不变地被液体向各个方向传递,这个规律被称为帕斯卡原理。
液压机就是根据这一原理工作的。
如图为它的工作原理图,其两活塞与同一容器的液体相接触,设小活塞的横截面积为S 1 ,加在它上面的压力为F 1,大活塞的横截面积为S 2.请你依据帕斯卡原理写出液体对大活塞压力F 2的数学表达式,并简要说明使用液压机的好处。
第2题图 第6题图 第10题图 第15题图3.马德堡半球实验证明了______________的存在;擦黑板时,粉笔擦与黑板之间的摩擦是_____________摩擦。
4.第一位用实验的方法测出大气压强数值的科学家是() A .托里拆利 B .牛顿 C .林利略 D .焦耳 5.下列现象中,不是利用大气压强的是:()A .钢笔吸墨水B .用吸管吸饮料C .抽水机把水从低处抽往高处D .用高压锅煮食物6.把一个烧瓶先放在开水中烫一会儿,然后立即固定在铁架台上,同时把一个剥了皮的熟鹌鹑蛋迅速塞入瓶口,如图所示。
你会看到鹌鹑蛋在_______作用下从瓶口__。
7.现有器材:玩具汽车、纸板、塑料尺、杯子、水,请任选以上器材,设计一个实验,并完成下表。
8.(杭州市)下列各图中,能够测出大气压值的实验是图()第8题图 第7题表9.做托里拆利实验时,测量的大气压强值比真实值小,其原因可能是:( ) A . 玻璃管放得不竖直 B .玻璃管内混入少量空气 C .水银槽内的水银太多 D .玻璃管粗细不均匀10.丙图丙用注射器吸取药液前,先将活塞推到底端,是为了_________。
11.某人用嘴将小空瓶内的空气吸出,小瓶马上挂在嘴唇上,原因是( )A.嘴把瓶子吸住 B.瓶内所剩的空气作用的结果C.嘴边的唾液把瓶粘住 D.大气压把小瓶压在嘴唇上12.一位小朋友的氢气球不小心脱手升到了空中,当气球升到高空时发生了破裂。
pai 定理 工程流体力学例题
例 1 开口容器内盛有液体,容器下部壁面有孔通大气。
显然在孔的不同高度上流出的速度也不同。
试计算通过此孔的流量Q 。
设自由面高度不变,不计摩擦,几何尺寸如图(4.13)所示。
解 出口面上的任一微面 dh b ⨯上的速度可以利用连续方程及动量方程求得
gh 2e
=V
式中h 为此微元面距自由面的高度。
出口体积流量为
})()2
{(2322b 2/32/32
/2/2/12
/2
/d H d
H g b dh h g b Vdh Q d H d H d H d H --+===⎰
⎰
+-+-
2
a e g p p H ρ+= 例2大容器有背压的小孔流出。
开口容器内盛有液体,容器下部有小孔,小孔与另一盛有液体的容器通,如图(4.14)所示。
两容器中自由液面高度分别为1H ,2H ,压力位a p ,设不计摩擦,1H ,2H 为常数,试求小孔流出速度。
解 小孔出口压力
(a )
在S A 面与e A 面之间应用伯努利方程
(b )
利用(a )、(b ),并注意到e
V V S <<,可得到出口速度公式
)g 221e H H V -=(
例3 文丘里管流量计
为了测量管道中的流量,可以将收缩—扩张管接到管道中去。
如图(4.15)所示。
通过测量颈部及来流段的压力差以确定流体的平均速度。
为了测量这个压力差,可以利用U 型管测压器。
试建立颈部
g
2g p 0g 2g p 2
e
e 2
a 1V
V H S ++=+=ρρ
)
1)(()(
)g
-
g
12121211
2
2
z p z p ρ
ρ
ρρρρ,
,
()(
-
-=---=++l l l l l l 2/1,
1221
2
222)]1)(()/-1g
2[(ρ
ρ---=
=
l l A A A V A Q 2/1,
1221
22)]1)(()/(-1g 2[A ρρ---=l l A V 流速与U 型管中液面高度差的关系。
解 对1—1,2—2截面利用连续方程与伯努利方程
1
2
21A A V V = (a)
z p
V z p V g
g
g g 22
2
2
1
1
21
22++
=++ρρ
(b)
由此两式可得 )()(2)/(122112
122
2
z p z p A A V g
g g +-+=-ρρ
(c ) 由此可见,只要能测出p p 1
2-
就可完全确定V
2。
再用静力学的关系式分析U 型管中各截面上的压力关系。
p
l z l l l g g 2
2212,
111
)()()g(z p
=
-----+ρρρ
由此可得
代入式(c )可得
管流流量Q 为
例4。