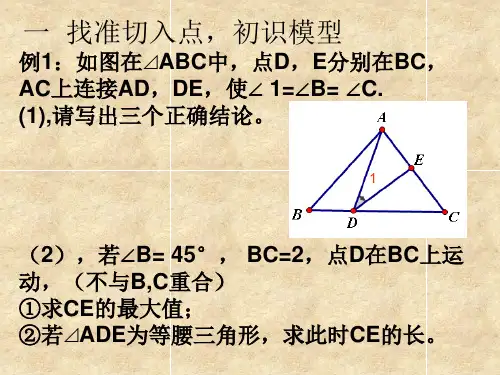
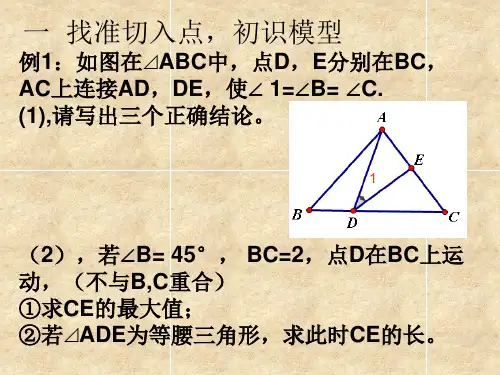
一线三等角模型PPT课件
- 格式:pptx
- 大小:632.56 KB
- 文档页数:18
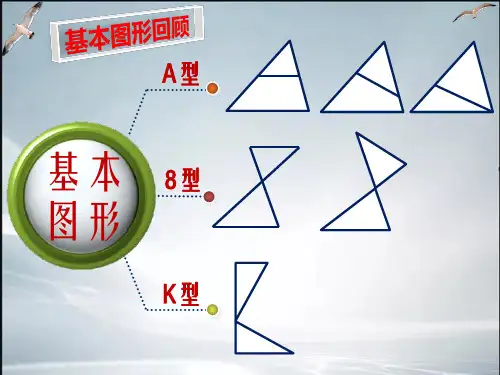


《相似三角形之一线三等角》教学ppt课件2023-10-26CATALOGUE目录•引言•相似三角形基本概念•一线三等角定理及其应用•课堂活动与练习•总结与回顾01引言•相似三角形是初中数学的重要内容,而一线三等角是相似三角形的一种重要类型。
通过学习本课,学生能够深入理解相似三角形的性质和判定方法,提高数学思维和解决问题的能力。
课程背景课程目标学会如何利用一线三等角判定两个三角形相似;掌握一线三等角的定义和性质;培养学生的自主学习和合作学习能力。
通过案例分析,培养学生的数学思维和解决问题的能力;教学策略利用PPT课件引导学生逐步深入学习;采用讲解、示范、小组讨论等多种教学方法,帮助学生掌握知识;通过案例分析,让学生了解一线三等角的应用;组织课堂练习和小组讨论,加深学生对知识的理解和应用。
02相似三角形基本概念如果两个三角形三边对应成比例,那么这两个三角形相似。
定义如果$\frac{a}{b} = \frac{c}{d}$,那么$\bigtriangleup ABC\backsim \bigtriangleup DEF$。
数学符号表示相似三角形的定义相似三角形的性质对应角相等相似三角形对应角相等,可以用$\bigtriangleup ABC \backsim \bigtriangleup DEF$推出$\angle A =\angle E$,$\angle B = \angle F$,$\angle C = \angle D$。
对应边成比例相似三角形对应边成比例,可以用$\bigtriangleup ABC \backsim \bigtriangleup DEF$推出$\frac{a}{d} = \frac{b}{e} = \frac{c}{f}$。
定义法根据相似三角形的定义进行判断,即判断两个三角形三边对应成比例。
平行线法通过平行线构造相似三角形,即利用平行线的性质,将两个三角形放在平行线上,通过移动使得对应边成比例,从而证明两个三角形相似。