化简下列逻辑函数要求表达式尽量简单-浙江大学
- 格式：doc
- 大小：357.00 KB
- 文档页数：1
文档推荐
-
15.3.5 卡诺图化简逻辑函数练习题页数:5
-
逻辑函数的公式化简方法页数:3
-
逻辑函数的公式化简方法页数:5
-
逻辑函数化简题目页数:8
下载文档原格式
合集下载
2.5逻辑函数的化简(2011)
= BC D + BC D = BD
消去B
11 10
结论： 1、 2 n 个最小项合并，消去n 个变量。 2、消去K圈中变量取值发生过 变化的量。保留取值没有变 化的量。
ABC D + ABC D + ABC D + ABC D
消去A、C
A BCD + ABCD + ABCD + A BCD + ABC D + ABC D + ABC D + ABC D = ACD + ACD + AC D + AC D = CD + C D = C
消去A、B、D
4、 用卡诺图化简逻辑函数 （1）求最简与或式 化简的步骤： • 作出逻辑函数的卡诺图； • 圈卡诺圈； • 将每个卡诺圈中的最小项合并成相应的与项。 圈卡诺圈的原则： 在卡诺图上，以最少的卡诺圈数和尽可能大的卡诺圈覆盖所有填1的 方格。（即：最小覆盖原则） 注释： • 将 2 n个相邻的填1方格圈起来，圈子尽可能大； • 所有填1格都必须被圈过，在此前提下K圈的个数尽可能少； • 任何一个填1格可以被不同的K圈多次圈过，但如果在一个K圈中， 所有的1格均已被别的K圈圈过，则该圈为多余的。
F = A BC + ABC + D + AD
AB CD
01
11
10
00 01
11 10
1 0 0 1
1 0 1 0
1 0 1 0
0 1 0 1 1 1 1 1 1 1 1 1 1 1
原则：分别寻找各与项中变量相交的小方格填1. （0——反变量，1——原变量）
（3）由或与式填卡诺图（填0） 举例：
F = ∏ M (0, 2, 6) = ( A + B + C )( A + B + C )( A + B + C )
消去B
11 10
结论： 1、 2 n 个最小项合并，消去n 个变量。 2、消去K圈中变量取值发生过 变化的量。保留取值没有变 化的量。
ABC D + ABC D + ABC D + ABC D
消去A、C
A BCD + ABCD + ABCD + A BCD + ABC D + ABC D + ABC D + ABC D = ACD + ACD + AC D + AC D = CD + C D = C
消去A、B、D
4、 用卡诺图化简逻辑函数 （1）求最简与或式 化简的步骤： • 作出逻辑函数的卡诺图； • 圈卡诺圈； • 将每个卡诺圈中的最小项合并成相应的与项。 圈卡诺圈的原则： 在卡诺图上，以最少的卡诺圈数和尽可能大的卡诺圈覆盖所有填1的 方格。（即：最小覆盖原则） 注释： • 将 2 n个相邻的填1方格圈起来，圈子尽可能大； • 所有填1格都必须被圈过，在此前提下K圈的个数尽可能少； • 任何一个填1格可以被不同的K圈多次圈过，但如果在一个K圈中， 所有的1格均已被别的K圈圈过，则该圈为多余的。
F = A BC + ABC + D + AD
AB CD
01
11
10
00 01
11 10
1 0 0 1
1 0 1 0
1 0 1 0
0 1 0 1 1 1 1 1 1 1 1 1 1 1
原则：分别寻找各与项中变量相交的小方格填1. （0——反变量，1——原变量）
（3）由或与式填卡诺图（填0） 举例：
F = ∏ M (0, 2, 6) = ( A + B + C )( A + B + C )( A + B + C )
2.6 逻辑函数的化简方法
A
C
23
2.
R= BC +ABD + ACD AB+AC=0（约束条件） D 1 B 1 1 R=BC +CD +BD A C
1 1 1
24
2.6.4卡诺图的运算 1、判断逻辑函数相等 2、卡诺图的或运算：
C 1 1 +
卡诺图完全相同
C 1
A
1
A
1
B
1
B 将对应小方格中的 值求逻辑和 1 A
C 1
1
B
1
25
3、卡诺图的与运算：
C
1 1 1 . 1 1CΒιβλιοθήκη AA1 B
B 将对应小方格中的 值求逻辑乘
C
1
A B 1
26
4、卡诺图的异或运算：
C 1 A B 1 + A 1
C
1
1
B
1
将对应小方格中的 值相异或
C 1
A
1 B
27
例:X=AB+BC+CD+AD
Y=AB+BD+BD+AC
Z=ABD+ACD 试用卡诺图求:
8
D
1 5 3 2
1
1
7
1
6
13
9
15
11
14
10
1
A
F= CD +ABD +BD
1
C
16
“两个最少”原则：
1、变量最少原则：包围圈尽可能的大，但 变量的个数必须是2n;与中轴线对称的小方格 也是相邻项。
2、与项最少原则：包围圈的数量最少，画 圈时应该使每个包围圈至少包含一个没被包 围过的方格。
数字系统答案
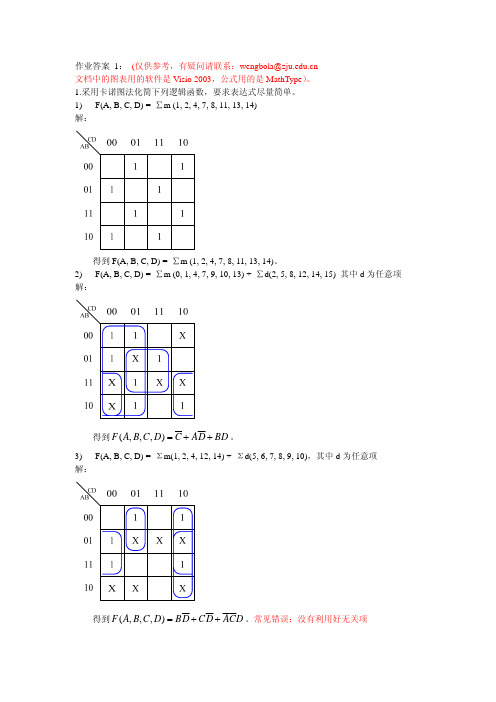
作业答案 1： (仅供参考，有疑问请联系：wengbola@文档中的图表用的软件是Visio 2003，公式用的是MathType ）。
1.采用卡诺图法化简下列逻辑函数，要求表达式尽量简单。
1) F(A, B, C, D) = ∑m (1, 2, 4, 7, 8, 11, 13, 14)解：得到F(A, B, C, D) = ∑m (1, 2, 4, 7, 8, 11, 13, 14)。
2) F(A, B, C, D) = ∑m (0, 1, 4, 7, 9, 10, 13) + ∑d(2, 5, 8, 12, 14, 15) 其中d 为任意项 解：得到(,,,)F A B C D C AD BD =++。
3) F(A, B, C, D) = Σm(1, 2, 4, 12, 14) + Σd(5, 6, 7, 8, 9, 10)，其中d 为任意项 解：得到(,,,)F A B C D BD CD ACD =++。
常见错误：没有利用好无关项4) (,,,)Y A B C D ABD ABC BCD ABCD ABCD =++++解：得到(,,,)Y A B C D ABC ABC BCD BCD =+++。
常见错误：多画上图中的红色框5) Y(A,B,C,D) = ∑m(0, 2, 3, 4, 8) + ∑d (10, 11,12,13,14,15)，其中 d 为任意项 解：得到(,,,)Y A B C D CD BC =+。
6) (,,,)()()()()()Y A B C D A B C D A B A B D B C B C D =+++++++++解：得到(,,,)Y A B C D BD ACD =+。
常见错误：最大项表示时卡诺图画错2.将下面函数化简为最简与或式，不必考虑冒险。
1) Y AD ABC ABD ABC D =+++, 约束条件为：0ABC ABD ACD BCD +++= 解：得到Y AD AD ABC =++。
逻辑函数化简题目
= AB + AB ⋅ AB ⋅ C = AB + ( A + B)( A + B)C = AB + ABC + ABC
= AB(C + C ) + ABC + ABC = ABC + ABC + ABC + ABC
=m7+m6+m3+m5=∑m（3,5,6,7）
卡诺图简化法
例3 用卡诺图化简
F(A B,C, D =∑ (0,1 2,5, 6, 7,8,9,13 , ) m , ,14)
AC D
B C
BD
11
AC
F = AC+ AD+ B +B + ACD D C
AD
10
例10：某逻辑函数输入是8421 10：某逻辑函数输入是8421BCD码，其逻辑表达式为： 码 其逻辑表达式为： 8421 L（A,B,C,D）=∑ （1,4,5,6,7,9）+∑ （10,11,12,13,14,15） （ , ）=∑m（1,4,5,6,7,9）+∑d（10,11,12,13,14,15） 用卡诺图法化简该逻辑函数。 用卡诺图法化简该逻辑函数。 画出4变量卡诺图。 号小方格填入1 解：（1）画出4变量卡诺图。将1、4、5、6、7、9号小方格填入1； 10、11、12、13、14、15号小方格填入 号小方格填入× 将10、11、12、13、14、15号小方格填入×。 合并最小项，如图（ ）所示。注意， 方格不能漏。 （2）合并最小项，如图（a）所示。注意，1方格不能漏。×方格 根据需要，可以圈入，也可以放弃。 根据需要，可以圈入，也可以放弃。 写出逻辑函数的最简与—或表达式 或表达式: （3）写出逻辑函数的最简与 或表达式: 如果不考虑无关项，如图（b）所示，写出表达式为： 如果不考虑无关项，如图（b）所示，写出表达式为：
= AB(C + C ) + ABC + ABC = ABC + ABC + ABC + ABC
=m7+m6+m3+m5=∑m（3,5,6,7）
卡诺图简化法
例3 用卡诺图化简
F(A B,C, D =∑ (0,1 2,5, 6, 7,8,9,13 , ) m , ,14)
AC D
B C
BD
11
AC
F = AC+ AD+ B +B + ACD D C
AD
10
例10：某逻辑函数输入是8421 10：某逻辑函数输入是8421BCD码，其逻辑表达式为： 码 其逻辑表达式为： 8421 L（A,B,C,D）=∑ （1,4,5,6,7,9）+∑ （10,11,12,13,14,15） （ , ）=∑m（1,4,5,6,7,9）+∑d（10,11,12,13,14,15） 用卡诺图法化简该逻辑函数。 用卡诺图法化简该逻辑函数。 画出4变量卡诺图。 号小方格填入1 解：（1）画出4变量卡诺图。将1、4、5、6、7、9号小方格填入1； 10、11、12、13、14、15号小方格填入 号小方格填入× 将10、11、12、13、14、15号小方格填入×。 合并最小项，如图（ ）所示。注意， 方格不能漏。 （2）合并最小项，如图（a）所示。注意，1方格不能漏。×方格 根据需要，可以圈入，也可以放弃。 根据需要，可以圈入，也可以放弃。 写出逻辑函数的最简与—或表达式 或表达式: （3）写出逻辑函数的最简与 或表达式: 如果不考虑无关项，如图（b）所示，写出表达式为： 如果不考虑无关项，如图（b）所示，写出表达式为：
逻辑函数化简方法
逻辑函数化简方法
逻辑函数化简是将复杂的逻辑函数简化为更简洁的形式的过程。
以下是常见的逻辑函数化简方法：
1. 真值表方法：通过构造逻辑函数的真值表，观察不同输入值下函数值的变化规律来推导简化逻辑函数的形式。
2. 化简定律：通过逻辑运算的各种定律来对逻辑函数进行化简，常见的包括德摩根定律、分配律、结合律、交换律等。
3. 卡诺图方法：利用卡诺图来进行逻辑函数的化简。
卡诺图是一种用来表示逻辑函数的图表，通过观察卡诺图的模式，可以找到逻辑函数的最小项和最大项，并将其化简为更简单的形式。
4. 斯芬克斯化简方法：适用于较复杂的逻辑函数。
斯芬克斯化简方法是一种将逻辑函数分解为多个子函数，并利用分解后的子函数进行化简的方法。
这些方法可以单独使用，也可以结合使用，根据具体情况选择合适的方法来进行逻辑函数的化简。
1.2逻辑函数的化简方法
ABC ABC ABC ABC ABC ABC ABC ABC
000 001 010 011 100 0 m0 1 m1 2 m2 3 m3 4 m4 101 5 m5 110 111 6 m6 7 m7
4. 最小项是组成逻辑函数的基本单元 任何逻辑函数都是由其变量的若干个最小项构成， 任何逻辑函数都是由其变量的若干个最小项构成， 都可以表示成为最小项之和的形式。 都可以表示成为最小项之和的形式。 写出下列函数的标准与或式： [例] 写出下列函数的标准与或式：
= ABCD + ABC D + ABC D + ABC D m7 m6 m5 m4
= m7 +m6+m5 + m4 + m1 + m0 + m8
+ A BC D + A BC D + A BC D + A BC D m1 m0 m8 m0
与前面m 与前面 0 相重
= ∑m( 0 , 1 , 4 , 5 , 6 , 7 , 8 )
Y = F( A ,B ,C ) = AB + A C
[解] Y = AB(C + C ) + AC ( B + B )
= ABC + ABC + A B C + ABC
m6 m7 m1 m3
= m6 + m7 + m1 + m3
或 = ∑ (1 , 3 , 6 , 7) m
写出下列函数的标准与或式： [例] 写出下列函数的标准与或式：
二、逻辑函数的最简表达式及相互转换 最简与或式 Y = AB + A + BC 最简与或式 C
最简 与非-与非式 与非 与非式 最简或与非式 最简或与非式 最简与或非式 最简与或非式 最简或与式 最简或与式 核心
逻辑函数的化简
AB CD 00 01 11 10 00 1 0 0 1 01 1 0 0 1 11 × × × × 10 1 0 × ×
不利用随意项 的化简结果为：
Y AD AC D
利用随意项的化 简结果为：
Y D
3、变量互相排斥的逻辑函数的化简 在一组变量中，如果只要有一个变量取值为1，则其它变量 的值就一定为0，具有这种制约关系的变量叫做互相排斥的变量。 变量互相排斥的逻辑函数也是一种含有随意项的逻辑函数。
ＢＣ的公因子
3、卡诺图的性质 （1）任何两个（21个）标1的相邻最小项，可以合并为一项， 并消去一个变量（消去互为反变量的因子，保留公因子）。
AB C 0 1 00 1 0 01 0 1 11 0 1 10 1 0
A B C AB C BC
A BC ABC
AB CD 00 01 11 10 00 0 0 0 0 01 1 0 0 1 11 0 0 0 0
A BC A BC ABC ABC ( A C A C AC AC) B B
AB CD 00 01 11 10 00 0 1 0 0 01 1 1 1 1 11 0 1 1 0 10 0 1 0 0
CD
AB
AB CD 00 01 11 10 00 0 1 1 0 01 1 0 0 1 11 1 0 0 1 10 0 1 1 0
ＡＤ
ＢＤ
AB CD 00 01 11 10 00 1 0 0 1 01 0 1 1 0 11 0 1 1 0 10 1 0 0 1
ＢＤ
ＢＤ
（3）任何8个（23个）标1的相邻最小 项，可以合并为一项，并消去3个变量。
AB CD 00 01 11 10 00 0 1 1 0 01 0 1 1 0 11 0 1 1 0 10 0 1 1 0
不利用随意项 的化简结果为：
Y AD AC D
利用随意项的化 简结果为：
Y D
3、变量互相排斥的逻辑函数的化简 在一组变量中，如果只要有一个变量取值为1，则其它变量 的值就一定为0，具有这种制约关系的变量叫做互相排斥的变量。 变量互相排斥的逻辑函数也是一种含有随意项的逻辑函数。
ＢＣ的公因子
3、卡诺图的性质 （1）任何两个（21个）标1的相邻最小项，可以合并为一项， 并消去一个变量（消去互为反变量的因子，保留公因子）。
AB C 0 1 00 1 0 01 0 1 11 0 1 10 1 0
A B C AB C BC
A BC ABC
AB CD 00 01 11 10 00 0 0 0 0 01 1 0 0 1 11 0 0 0 0
A BC A BC ABC ABC ( A C A C AC AC) B B
AB CD 00 01 11 10 00 0 1 0 0 01 1 1 1 1 11 0 1 1 0 10 0 1 0 0
CD
AB
AB CD 00 01 11 10 00 0 1 1 0 01 1 0 0 1 11 1 0 0 1 10 0 1 1 0
ＡＤ
ＢＤ
AB CD 00 01 11 10 00 1 0 0 1 01 0 1 1 0 11 0 1 1 0 10 1 0 0 1
ＢＤ
ＢＤ
（3）任何8个（23个）标1的相邻最小 项，可以合并为一项，并消去3个变量。
AB CD 00 01 11 10 00 0 1 1 0 01 0 1 1 0 11 0 1 1 0 10 0 1 1 0
第2讲 逻辑函数的公式化简法
例如： 例如： A(B+C) AB+AC 因为 所以
对偶 A+BC, 对偶 (A+B)(A+C), A(B+C)=AB+AC成立 成立, 成立 A+BC=(A+B)(A+C)亦成立。 亦成立。 亦成立
ห้องสมุดไป่ตู้
注意：为保持原式的逻辑优先关系， 应正确使用括号。 注意：为保持原式的逻辑优先关系， 应正确使用括号。
练习： 练习： 例
解
F = AB + A CD + BCDE
F = AB + A CD
例
解
F = ABC + ( A + C ) D + BD
F = ABC + AC D + BD = ABC + AC D
Y = ACE+ A + BC D+ BEC + DEC + A BE E
B = E ( AC + A + BC + DC + A) + BC D = E ( C + B + D+ A ) + B C D = E (B+ C + D) + AE + BC D
三、消因子法：利用 A+ AB = A+ B消去多余因子 A 消因子法： 。 [例 1. 2. 9] Y = AB+ AC + BD ]
解
= A+ B+ AC + BD = A+ B+C + D
= A (B+ B C) + A (B+ BC) = A (B+ C) + A (B+ C) B B C = A + AB+ A + AC = A + AB+C
[精品]1.3逻辑函数公式化简法
逻辑函数的公式法化简
[例] 证明公式 A BC ( A B)( A C ) [解] 方法2：真值表法 A B 0 0 0 0 0 1 0 1 1 0 1 0 1 1 1 1 C B C A BC A B A C ( A B)( A C ) 0 0 0 0 0 0 0 1 0 0 1 0 0 0 0 0 1 0 1 1 1 1 1 1 1 0 0 1 1 1 1 0 1 1 1 1 1 1 0 0 1 1 1 1 1 1 1 1
A ( BC B C ) A ( BC BC )
A B C A( B C ) A
逻辑函数的公式法化简
二、吸收法：
A AB A
[例 1] Y AB AD BE
A B AD BE A B
[例2] Y AB ACD BCD
) A
(3) A AB ( A A)( A B) A B (4) AB AC BC AB AC
(5) AB AB A B AB
逻辑函数的公式法化简
公式 (4) 证明：
AB AC BC AB AC
左 AB AC ( A A) BC A AB A
取反（即还原），最后用摩根定理去掉反号。
[例] 写出函数 Y AB AC 的最简或与式。
[ 解]
Y = ( A + B)( A + C) = AC + AB + BC
= AC + AB + BC
Y AB AC AB AC ( A B ) ( A C )
逻辑函数的公式法化简
相等
相等
逻辑函数的公式法化简
电工电子技术-逻辑函数的化简
（2）吸收法
运用公式 A AB A 消去多余的项，其中，A、B可以是
任意一个复杂的逻辑式。例如：
Y1 AB AC DEB AB
Y2 AB ABC ABD AB D E AB AB C D D E AB
（3）消去法
运用公式 A AB A B 消去多余的因子。例如：
例如：逻辑函数Y的卡诺图。 Y ABCD ABCD ABCD ABCD
ABCD ABCD ABCD ABCD
（3）用卡诺图化简逻辑函数式 使用卡诺图化简逻辑函数所依据的原理是：具有相邻性 的最小项可以合并消去不同的因子。 ①2个相邻的最小项结合（用一个包围圈表示），可以消 去1个取值不同的变量而合并为1项，如下图所示。
00 01 11 10 00
01 11 10
②4个相邻的最小项结合（用一个包围圈表示），可以消 去2个取值不同的变量而合并为l项，如下图所示。
00 01 11 10 00
01 11 10
③8个相邻的最小项结合（用一个包围圈表示），可以消 去3个取值不同的变量而合并为l项，如下图所示。
00 01 11 10 00
②化简具有无关项的逻辑函数 在卡诺图中用×表示无关项。使用卡诺图化简逻辑函数 式时，要充分利用无关项可以当0也可以当1的特点，尽量扩 大卡诺圈，使逻辑函数式更简。
（2）卡诺图
卡诺图就是将n变量的全部最小项各用一个小方块表示，
并使具有逻辑相邻性的最小项在几何位置上也相邻的排列起 来所得的图形。下图所示为2到4变量最小项的卡诺图。
若要画出某一逻辑函数的卡诺图，只需将该逻辑函数式 化为最小项之和的标准形式后，在卡诺图中这些最小项对应 的位置上填入1，在其余的位置上填入0即可。
1．公式化简法
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
数字电路2014
：浙江大学信息与通信工程研究所 liupeng@ 作业1：（上交时间：2014年3月6日）
1.采用卡诺图法化简下列逻辑函数，要求表达式尽量简单。
1) F(A, B,C, D) = ∑m (1, 2, 4, 7, 8, 11, 13, 14)
2) F (A, B, C, D) = ∑m (0, 1, 4, 7, 9, 10, 13) + ∑d(2, 5, 8, 12, 14, 15) 其中d 为任意项
3) F(A,B,C,D)=Σm(1,2,4,12,14) + Σd(5,6,7,8,9,10)，其中d 为任意项
4) Y A,B,C,D)=A BD+ABC+BCD+AB CD+A B CD （
5) Y(A ,B,C,D) = ∑m(0, 2, 3, 4, 8) + ∑d (10, 11,12,13,14,15)，其中d 为任意项
6) (,,,)()()()()()Y A B C D A B C D A B A B D B C B C D =+++++++++
2.将下面函数化简为最简与或式，不必考虑冒险。
1) Y AD ABC ABD ABCD =+++, 约束条件为：ABC+ABD+ACD+BCD = 0
2) (1,3,4,6,7,9,11,12,14,15)Y M =∏
3) ()()Y AB AC BD ABCD ACD BCD BC =+++++
3.能实现任何逻辑函数的逻辑门的集合，被称为逻辑门的完全集。
已知二输入与门、二输入或门和非门为一个完全集。
试证明：二输入或门、异或门为逻辑门的完全集。
4．采用公式法将下面的逻辑函数化简成最简与或式，并用与非门实现。
()()Y AB D AB B D ABE ADE =++++
5．用权6，3，1，1将十进制表示为含权的二进制码。
6．列出真值表：
输入是3位二进制，输出为3位循环码
7．用最小项之和与最大项之积来表示下列函数
(,,,)F A B C D BD AD BD =++
8．用异或门和与门实现下面的布尔表达式。
F ABCD ABCD ABCD ABCD =+++
9. 和8421BCD 码（1010100）等值的二进制数为 。
10．一个有n 个变量的逻辑函数，如果它的最小项表达式由k 个最小项组成，则它的最大
项表达式将由 个最大项组成。
11．一个格雷码的前一个码是0101，后一个是1100，这个格雷码是 。
12.有函数 1F (A,B,C,D)=ABCD+BCD+AB D+ABCD+AD
2F (A,B,C,D)=CD+ABCD+BD+ACD+BCD
试求函数312F (A,B,C,D)=F F ⊕的最简与或表达式。