分别是-正弦-余弦-正切-余切-正割-余割(同名18339)

三角函数： 正弦, 余弦, 正切, 正割, 余割, 余切三角函数维基百科，自由的百科全书在数学中，三角函数（也叫做圆函数）是角的函数；它们在研究三角形和建模周期现象和许多其他应用中是很重要的。

三角函数通常定义为包含这个角的直角三角形的两个边的比率，也可以等价的定义为单位圆上的各种线段的长度。

更现代的定义把它们表达为无穷级数或特定微分方程的解，允许它们扩展到任意正数和负数值，甚至是复数值。

三角函数在数学中属于初等函数里的超越函数的一类函数。

它们本质上是任意角的集合与一个比值的集合的变量之间的映射。

由于三角函数具有周期性，所以并不具有单射函数（亦称为单调函数）意义上的反函数。

三角函数在复数中有重要的应用，在物理学中也是常用的工具。

三角函数一般用于计算三角形（通常为直角三角形）中未知长度的边和未知的角度，在导航系统，工程学以及物理学方面都有广泛的用途。

其在基本物理中的一个常见用途是将矢量转换到笛卡尔坐标系中。

现代比较常用的三角函数有6个，其中Sin 和Cos 还常用于模拟周期函数现象，比如说声波和光波，谐振子的位置和速度，光照强度和白昼长度，过去一年中的平均气温变化等等。

目录1 基本函数■2 罕见函数■3 历史■4 直角三角定义■ 4.1 直角三角形中■4.2 直角坐标系中■5 单位圆定义■6 级数定义■ 6.1 与指数函数和复数的联系■7 微分方程定义■7.1 弧度的重要性■8 恒等式■8.1 微积分■8.2 利用函数方程定义三角函数■9 计算■9.1 三角函数的特殊值■10 反三角函数■11 性质和应用■11.1 正弦定理■11.2 余弦定理■11.3 正切定理■直角三角形。

11.4 周期函数■12 注释■13 参考文献■14 参见■15 外部链接■基本函数如右图，当平面上的三点A 、B 、C 的连线，、、，，其中为与的而言斜边（hypotenuse ）函数英语简写定义关系正弦Sinesin 余弦Cosinecos余切Cotangentcot 正割Secantsec注：中国大陆早期教科书中多将正切、余切写作tg，ctg，现已废弃不用。

高中数学三角函数总结三角函数是数学中重要的概念之一，广泛应用于几何、物理和工程等领域。

它们是描述角度与直角三角形边长比例关系的函数，包括正弦、余弦、正切、余切、正割和余割。

下面是对高中数学三角函数的总结。

1. 正弦函数（sin）：正弦函数描述了角度与直角三角形斜边与其对边之比的关系。

在数学中，我们用sin(θ)来表示θ角的正弦值。

正弦函数的定义域是所有实数，值域是[-1, 1]。

正弦函数的图像在0到360度之间周期性重复，它在0度和180度时等于0，在90度时等于1，在270度时等于-1。

2. 余弦函数（cos）：余弦函数描述了角度与直角三角形斜边与其邻边之比的关系。

在数学中，我们用cos(θ)来表示θ角的余弦值。

余弦函数的定义域是所有实数，值域也是[-1, 1]。

余弦函数的图像与正弦函数的图像相似，但在0度时取1，在180度时取-1。

3. 正切函数（tan）：正切函数描述了角度与直角三角形对边与邻边之比的关系。

在数学中，我们用tan(θ)来表示θ角的正切值。

正切函数的定义域是除了90度、270度等所有能让余弦函数为0的角度之外的所有实数，值域是所有实数。

正切函数的图像是一个周期性的波浪线，它在0度和180度时等于0，在90度时等于无穷大。

4. 余切函数（cot）：余切函数描述了角度与直角三角形邻边与对边之比的关系。

在数学中，我们用cot(θ)来表示θ角的余切值。

余切函数的定义域是除了0度、180度等所有能让正弦函数为0的角度之外的所有实数，值域是所有实数。

余切函数的图像是正切函数图像的镜像。

5. 正割函数（sec）：正割函数描述了角度与直角三角形斜边与其邻边之比的倒数的关系。

在数学中，我们用sec(θ)来表示θ角的正割值。

正割函数的定义域是除了90度、270度等所有能让余弦函数为0的角度之外的所有实数，值域是实数的绝对值大于或等于1。

正割函数的图像是余弦函数图像的倒数。

6. 余割函数（csc）：余割函数描述了角度与直角三角形斜边与其对边之比的倒数的关系。

初中三角函数公式及定理大全1、正弦定理：在三角形中，各边和它所对的角的正弦的比相等，即a/sinA=b/sinB=c/sinC=2R 。

（其中R为外接圆的半径），2、第一余弦定理：三角形中任意一边等于其他两边以及对应角余弦的交叉乘积的和，即a=c cosB + b cosC。

初中三角函数公式及定理大全1锐角三角函数定义:锐角角A的正弦(sin),余弦(cos)和正切(tan),余切(cot)以及正割(sec)，余割(csc)都叫做角A的锐角三角函数。

正弦(sin)：对边比斜边，即sinA=a/c余弦(cos)：邻边比斜边，即cosA=b/c正切(tan)：对边比邻边，即tanA=a/b余切(cot)：邻边比对边，即cotA=b/a正割(sec)：斜边比邻边，即secA=c/b余割(csc)：斜边比对边，即cscA=c/a初中三角函数公式及定理大全2互余角的关系sin(π-α)=cosα, cos(π-α)=sinα,tan(π-α)=cotα, cot(π-α)=tanα.积的关系sinα=tanα·cosαcosα=cotα·sinαtanα=sinα·secαcotα=cosα·cscαsecα=tanα·cscαcscα=secα·cotα初中三角函数公式及定理大全3平方关系sin^2(α)+cos^2(α)=1tan^2(α)+1=sec^2(α)cot^2(α)+1=csc^2(α)倒数关系tanα·cotα=1sinα·cscα=1cosα·secα=1初中三角函数公式及定理大全4三角函数的和差化积公式sinA+sinB=2sin[(A+B)/2]cos[(A-B)/2]sinA-sinB=2cos[(A+B)/2]sin[(A-B)/2]cosA+cosB=2cos[(A+B)/2]cos[(A-B)/2]cosA-cosB=-2sin[(A+B)/2]sin[(A-B)/2]tanA+tanB=sin(A+B)/cosAcosB=tan(A+B)(1-tanAtanB) tanA-tanB=sin(A-B)/cosAcosB=tan(A-B)(1+tanAtanB)。

分别是-正弦-余弦-正切-余切-正割-余割维基百科正弦性质奇偶性奇定义域(-∞,∞)到达域[-1,1]周期2π特定值当x=00当x=+∞N/A当x=-∞N/A((2k+½)π,1最大值)((2k-½)π,-1最小值)其他性质渐近线N/A根kπ临界点kπ-π/2 拐点kπ不动点0k是一个整数.余弦性质奇偶性偶定义域(-∞,∞)到达域[-1,1]周期2π特定值当x=00当x=+∞N/A当x=-∞N/A最大值(2kπ,1)最小值((2k+1)π,-1)其他性质渐近线N/A根kπ-π/2临界点kπ拐点kπ-π/2不动点0k是一个整数.正切性质奇偶性奇{x|x≠kπ+π/2，定义域k∈Z}到达域(-∞,∞)周期π特定值性质奇偶性奇{x∈R〡x≠kπ，定义域k∈Z}到达域(-∞,∞)周期π特定值当x=00当x=+∞N/A当x=-∞N/A最大值∞最小值-∞其他性质渐近线N/A根kπ+不动点0k是一个整数.正割性质奇偶性偶{x|x≠kπ+π/2，定义域k∈Z}到达域|secx|≥1周期2π特定值k是一个整数.余割性质奇偶性奇定义域{x|x≠kπ，k∈Z} 到达域|csc x|≥1周期2π特定值当x=00当x=+∞N/A当x=-∞N/A(最大值,∞)(最小值,-∞)其他性质渐近线N/A根无实根临界点kπ-π/2拐点kπ不动点0k是一个整数.反正弦性质奇偶性奇定义域[-1, 1]到达域周期N/A 特定值当x=00当x=+∞N/A 当x=-∞N/A 最大值最小值其他性质渐近线N/A 根0反余弦性质奇偶性非奇非偶函数定义域[-1, 1]到达域周期N/A 特定值当x=0当x=+∞N/A 当x=-∞N/A最大值最小值其他性质渐近线N/A 根 1反正切性质奇偶性奇函数定义域实数集到达域周期N/A 特定值当x=00当x=+∞当x=-∞其他性质渐近线根0拐点原点名称常用符号定义定义域值域反正弦反余弦反正切反余切反正割反余割百度文库下载分别是正弦余弦正切余切正割余割角θ的所有三角函数(见:函数图形曲线)在平面直角坐标系xOy中，从点O引出一条射线OP，设旋转角为θ，设OP=r，P点的坐标为（x，y）有正弦函数sinθ=y/r余弦函数cosθ=x/r正切函数tanθ=y/x余切函数cotθ=x/y正割函数secθ=r/x余割函数cscθ=r/y（斜边为r，对边为y，邻边为x。

分别是正弦余弦正切余切正割余割角θ的所有三角函数(见:函数图形曲线)在平面直角坐标系xOy中，从点O引出一条射线OP，设旋转角为θ，设OP=r，P点的坐标为（x，y）有正弦函数sinθ=y/r余弦函数cosθ=x/r正切函数tanθ=y/x余切函数cotθ=x/y正割函数secθ=r/x余割函数cscθ=r/y（斜边为r，对边为y，邻边为x。

）以及两个不常用，已趋于被淘汰的函数：正矢函数versinθ=1-cosθ余矢函数coversθ=1-sinθ正弦（sin）:角α的对边比上斜边余弦（cos）:角α的邻边比上斜边正切（tan）:角α的对边比上邻边余切（cot）:角α的邻边比上对边正割（sec）:角α的斜边比上邻边余割（csc）:角α的斜边比上对边[编辑本段]同角三角函数间的基本关系式：·平方关系：sin^2α＋cos^2α＝11＋tan^2α＝sec^2α1＋cot^2α＝csc^2α·积的关系：sinα=tanα×cosαcosα=cotα×sinαtanα=sinα×secαcotα=cosα×cscαsecα=tanα×cscαcscα=secα×cotα·倒数关系：tanα·cotα＝1sinα·cscα＝1cosα·secα＝1商的关系：sinα/cosα＝tanα＝secα/cscαcosα/sinα＝cotα＝cscα/secα直角三角形ABC中,角A的正弦值就等于角A的对边比斜边,余弦等于角A的邻边比斜边正切等于对边比邻边,·[1]三角函数恒等变形公式·两角和与差的三角函数：cos(α+β)=cosα·cosβ-sinα·sinβcos(α-β)=cosα·cosβ+sinα·sinβsin(α±β)=sinα·cosβ±cosα·sinβtan(α+β)=(tanα+tanβ)/(1-tanα·tanβ)tan(α-β)=(tanα-tanβ)/(1+tanα·tanβ)·三角和的三角函数：sin(α+β+γ)=sinα·cosβ·cosγ+cosα·sinβ·cosγ+cosα·cosβ·sinγ-sinα·si nβ·sinγcos(α+β+γ)=cosα·cosβ·cosγ-cosα·sinβ·sinγ-sinα·cosβ·sinγ-si nα·sin β·cosγtan(α+β+γ)=(tanα+tanβ+tanγ-tanα·tanβ·tanγ)/(1-tanα·tanβ-tanβ·tanγ-tanγ·tanα)·辅助角公式：Asinα+Bcosα=(A²+B²)^(1/2)sin(α+arctan(B/A))，其中sint=B/(A²+B²)^(1/2)cost=A/(A²+B²)^(1/2)tant=B/AAsinα-Bcosα=(A²+B²)^(1/2)cos(α-t)，tant=A/B·倍角公式：sin(2α)=2sinα·cosα=2/(tanα+cotα)cos(2α)=cos²(α)-sin²(α)=2cos²(α)-1=1-2sin² (α)tan(2α)=2tanα/[1-tan²(α)]·三倍角公式：sin(3α)=3sinα-4sin³(α)=4sinα·sin(60+α)sin(60-α)cos(3α)=4cos³(α)-3cosα=4cosα·cos(60+α)cos(60-α)tan(3α)=tana·tan(π/3+a)·tan(π/3-a)·半角公式：sin(α/2)=±√((1-cosα)/2)cos(α/2)=±√((1+cosα)/2)tan(α/2)=±√((1-cosα)/(1+cosα))=sinα/(1+cosα)=(1-cosα)/sinα·降幂公式sin²(α)=(1-cos(2α))/2=versin(2α)/2cos²(α)=(1+cos(2α))/2=covers(2α)/2tan²(α)=(1-cos(2α))/(1+cos(2α))·万能公式：sinα=2tan(α/2)/[1+tan²(α/2)]cosα=[1-tan²(α/2)]/[1+tan²(α/2)]tanα=2tan(α/2)/[1-tan²(α/2)]·积化和差公式：sinα·cosβ=(1/2)[sin(α+β)+sin(α-β)]cosα·sinβ=(1/2)[sin(α+β)-sin(α-β)]cosα·cosβ=(1/2)[cos(α+β)+cos(α-β)]sinα·sinβ=-(1/2)[cos(α+β)-cos(α-β)]·和差化积公式：sinα+sinβ=2sin[(α+β)/2]cos[(α-β)/2]sinα-sinβ=2cos[(α+β)/2]sin[(α-β)/2]cosα+cosβ=2cos[(α+β)/2]cos[(α-β)/2]cosα-cosβ=-2sin[(α+β)/2]sin[(α-β)/2]·推导公式tanα+cotα=2/sin2αtanα-cotα=-2cot2α1+cos2α=2cos²α1-cos2α=2sin²α1+sinα=(sinα/2+cosα/2)²·其他：sinα+sin(α+2π/n)+sin(α+2π*2/n)+sin(α+2π*3/n)+……+sin[α+2π*(n-1) /n]=0cosα+cos(α+2π/n)+cos(α+2π*2/n)+cos(α+2π*3/n)+……+cos[α+2π* (n-1)/n]=0以及sin²(α)+sin²(α-2π/3)+sin²(α+2π/3)=3/2tanAtanBtan(A+B)+tanA+tanB-tan(A+B)=0cosx+cos2x+...+cosnx=[sin(n+1)x+sinnx-sinx]/2sinx证明：左边=2sinx(cosx+cos2x+...+cosnx)/2sinx=[sin2x-0+sin3x-sinx+sin4x-sin2x+...+sinnx-sin(n-2)x+sin(n+1)x-sin (n-1)x]/2sinx（积化和差）=[sin(n+1)x+sinnx-sinx]/2sinx=右边等式得证sinx+sin2x+...+sinnx=-[cos(n+1)x+cosnx-cosx-1]/2sinx证明:左边=-2sinx[sinx+sin2x+...+sinnx]/(-2sinx)=[cos2x-cos0+cos3x-cosx+...+cosnx-cos(n-2)x+cos(n+1)x-cos(n-1)x] /(-2sinx)=-[cos(n+1)x+cosnx-cosx-1]/2sinx=右边等式得证三倍角公式推导sin3a=sin(2a+a)=sin2acosa+cos2asina=2sina(1-sin²a)+(1-2sin²a)sina=3sina-4sin³acos3a=cos(2a+a)=cos2acosa-sin2asina=(2cos²a-1)cosa-2(1-sin²a)cosa=4cos³a-3cosasin3a=3sina-4sin³a=4sina(3/4-sin²a)=4sina[(√3/2)²-sin²a]=4sina(sin²60°-sin²a)=4sina(sin60°+sina)(sin60°-sina)=4sina*2sin[(60+a)/2]cos[(60°-a)/2]*2sin[(60°-a)/2]cos[(60°+a)/2]=4sinasin(60°+a)sin(60°-a)cos3a=4cos³a-3cosa=4cosa(cos²a-3/4)=4cosa[cos²a-(√3/2)²]=4cosa(cos²a-cos²30°)=4cosa(cosa+cos30°)(cosa-cos30°)=4cosa*2cos[(a+30°)/2]cos[(a-30°)/2]*{-2sin[(a+30°)/2]sin[(a-30°)/2]} =-4cosasin(a+30°)sin(a-30°)=-4cosasin[90°-(60°-a)]sin[-90°+(60°+a)]=-4cosacos(60°-a)[-cos(60°+a)]=4cosacos(60°-a)cos(60°+a)上述两式相比可得tan3a=tanatan(60°-a)tan(60°+a)[编辑本段]三角函数的诱导公式公式一：设α为任意角，终边相同的角的同一三角函数的值相等：sin（2kπ＋α）＝sinαcos（2kπ＋α）＝cosαtan（2kπ＋α）＝tanαcot（2kπ＋α）＝cotα公式二：设α为任意角，π+α的三角函数值与α的三角函数值之间的关系：sin（π＋α）＝－sinαcos（π＋α）＝－cosαtan（π＋α）＝tanαcot（π＋α）＝cotα公式三：任意角α与-α的三角函数值之间的关系：sin（－α）＝－sinαcos（－α）＝cosαtan（－α）＝－tanαcot（－α）＝－cotα公式四：利用公式二和公式三可以得到π-α与α的三角函数值之间的关系：sin（π－α）＝sinαcos（π－α）＝－cosαtan（π－α）＝－tanαcot（π－α）＝－cotα公式五：利用公式一和公式三可以得到2π-α与α的三角函数值之间的关系：sin（2π－α）＝－sinαcos（2π－α）＝cosαtan（2π－α）＝－tanαcot（2π－α）＝－cotα公式六：π/2±α及3π/2±α与α的三角函数值之间的关系：sin（π/2＋α）＝cosαcos（π/2＋α）＝－sinαtan（π/2＋α）＝－cotαcot（π/2＋α）＝－tanαsin（π/2－α）＝cosαcos（π/2－α）＝sinαtan（π/2－α）＝cotαcot（π/2－α）＝tanαsin（3π/2＋α）＝－cosαcos（3π/2＋α）＝sinαtan（3π/2＋α）＝－cotαcot（3π/2＋α）＝－tanαsin（3π/2－α）＝－cosαcos（3π/2－α）＝－sinαtan（3π/2－α）＝cotαcot（3π/2－α）＝tanα(以上k∈Z)补充：6×9＝54种诱导公式的表格以及推导方法（定名法则和定号法定名法则90°的奇数倍+α的三角函数，其绝对值与α三角函数的绝对值互为余函数。

函数名正弦余弦正切余切正割余割这些函数都是三角函数的一部分，它们在数学和物理中都有广泛的应用。

以下是对这些函数的基本介绍：1.正弦函数（Sine Function）和余弦函数（Cosine Function）：正弦函数和余弦函数都与三角形的边长有关。

在直角三角形中，正弦函数是三角形的对边（opposite）与斜边（hypotenuse）的比值，记为sin(x)；余弦函数是三角形的邻边（adjacent）与斜边的比值，记为cos(x)。

正弦和余弦函数的图像都是周期性的，这意味着它们在一定间隔内重复。

2.正切函数（Tangent Function）和余切函数（Cotangent Function）：正切函数和余切函数是正弦函数和余弦函数的比值。

正切函数是正弦函数除以余弦函数，记为tan(x)；余切函数是余弦函数除以正弦函数，记为cot(x)。

正切函数的图像也是周期性的，但余切函数的图像并非周期性。

3.正割函数（Secant Function）和余割函数（Cosecant Function）：正割函数和余割函数分别是正弦函数和余弦函数的倒数。

正割函数是sec(x) = 1/cos(x)，余割函数是csc(x) = 1/sin(x)。

它们的图形也是周期性的。

这些函数在三角学中有着重要的应用。

例如，它们可以用来描述振动、波动、声音传播等物理现象。

在计算机图形学中，这些函数也常被用来生成旋转、缩放、平移等变换。

此外，这些函数在解决一些数学问题时也非常有用，比如求解极值、最优解、零点等。

除了基本的三角函数，还有许多派生出来的三角函数，如反正弦函数（Inverse Sine Function）、反余弦函数（Inverse Cosine Function）、反正切函数（Inverse Tangent Function）等。

这些函数的定义域是有限的，值域是整个实数集。

它们通常被用于求解一些方程的根，比如求解三角形的角度等。

函数名正弦余弦正切余切正割余割在平面直角坐标系xOy中，从点O引出一条射线OP，设旋转角为θ，设OP=r，P点的坐标为（x，y）有正弦函数sinθ=y/r余弦函数cosθ=x/r正切函数tanθ=y/x余切函数cotθ=x/y正割函数secθ=r/x余割函数cscθ=r/y（斜边为r，对边为y，邻边为x。

）以及两个不常用，已趋于被淘汰的函数：正矢函数versinθ =1-cosθ余矢函数coversθ =1-sinθ正弦（sin）:角α的对边比上斜边余弦（cos）:角α的邻边比上斜边正切（tan）:角α的对边比上邻边余切（cot）:角α的邻边比上对边正割（sec）:角α的斜边比上邻边余割（csc）:角α的斜边比上对边[编辑本段]同角三角函数间的基本关系式：·平方关系：sin²(α)+cos²(α)=1 cos²(a)=(1+cos2a)/2tan²(α)+1=sec²(α) sin²(a)=(1-cos2a)/2cot²(α)+1=csc²(α)·积的关系：sinα=tanα*cosαcosα=cotα*sinαtanα=sinα*secαcotα=cosα*cscαsecα=tanα*cscαcscα=secα*cotα·倒数关系：tanα·cotα=1sinα·cscα=1cosα·secα=1直角三角形ABC中,角A的正弦值就等于角A的对边比斜边,余弦等于角A的邻边比斜边正切等于对边比邻边,·三角函数恒等变形公式·两角和与差的三角函数：cos(α+β)=cosα·cosβ-sinα·sinβcos(α-β)=cosα·cosβ+sinα·sinβsin(α±β)=sinα·cosβ±cosα·sinβtan(α+β)=(tanα+tanβ)/(1-tanα·tanβ)tan(α-β)=(tanα-tanβ)/(1+tanα·tanβ)·三角和的三角函数：sin(α+β+γ)=sinα·cosβ·cosγ+cosα·sinβ·cosγ+cosα·cosβ·sinγ-sinα·sinβ·sinγcos(α+β+γ)=cosα·cosβ·cosγ-cosα·sinβ·sinγ-sinα·cosβ·sinγ-sinα·sinβ·cosγtan(α+β+γ)=(tanα+tanβ+tanγ-tanα·tanβ·tanγ)/(1-tanα·tanβ-tanβ·tanγ-tanγ·tanα)·辅助角公式：Asinα+Bcosα=(A²+B²)^(1/2)sin(α+t)，其中sint=B/(A²+B²)^(1/2)cost=A/(A²+B²)^(1/2)tant=B/AAsinα+Bcosα=(A²+B²)^(1/2)cos(α-t)，tant=A/B·倍角公式：sin(2α)=2sinα·cosα=2/(tanα+cotα)cos(2α)=cos²(α)-sin²(α)=2cos²(α)-1=1-2sin²(α)tan(2α)=2tanα/[1-tan²(α)]·三倍角公式：sin(3α)=3sinα-4sin³(α)cos(3α)=4cos³(α)-3cosα·半角公式：sin(α/2)=±√((1-cosα)/2)cos(α/2)=±√((1+cosα)/2)tan(α/2)=±√((1-cosα)/(1+cosα))=sinα/(1+cosα)=(1-cosα)/sinα·降幂公式sin²(α)=(1-cos(2α))/2=versin(2α)/2cos²(α)=(1+cos(2α))/2=covers(2α)/2tan²(α)=(1-cos(2α))/(1+cos(2α))·万能公式：sinα=2tan(α/2)/[1+tan²(α/2)]cosα=[1-tan²(α/2)]/[1+tan²(α/2)]tanα=2tan(α/2)/[1-tan²(α/2)]·积化和差公式：sinα·cosβ=(1/2)[sin(α+β)+sin(α-β)]cosα·sinβ=(1/2)[sin(α+β)-sin(α-β)]cosα·cosβ=(1/2)[cos(α+β)+cos(α-β)]sinα·sinβ=-(1/2)[cos(α+β)-cos(α-β)]·和差化积公式：sinα+sinβ=2sin[(α+β)/2]cos[(α-β)/2]sinα-sinβ=2cos[(α+β)/2]sin[(α-β)/2]cosα+cosβ=2cos[(α+β)/2]cos[(α-β)/2]cosα-cosβ=-2sin[(α+β)/2]sin[(α-β)/2]·推导公式tanα+cotα=2/sin2αtanα-cotα=-2cot2α1+cos2α=2cos²α1-cos2α=2sin²α1+sinα=(sinα/2+cosα/2)²·其他：sinα+sin(α+2π/n)+sin(α+2π*2/n)+sin(α+2π*3/n)+……+sin[α+2π*(n-1)/n]=0cosα+cos(α+2π/n)+cos(α+2π*2/n)+cos(α+2π*3/n)+……+cos[α+2π*(n-1)/n]=0 以及sin²(α)+sin²(α-2π/3)+sin²(α+2π/3)=3/2tanAtanBtan(A+B)+tanA+tanB-tan(A+B)=0cosx+cos2x+...+cosnx= [sin(n+1)x+sinnx-sinx]/2sinx证明：左边=2sinx(cosx+cos2x+...+cosnx)/2sinx=[sin2x-0+sin3x-sinx+sin4x-sin2x+...+ sinnx-sin(n-2)x+sin(n+1)x-sin(n-1)x]/2sinx （积化和差）=[sin(n+1)x+sinnx-sinx]/2sinx=右边等式得证sinx+sin2x+...+sinnx= - [cos(n+1)x+cosnx-cosx-1]/2sinx证明:左边=-2sinx[sinx+sin2x+...+sinnx]/(-2sinx)=[cos2x-cos0+cos3x-cosx+...+cosnx-cos(n-2)x+cos(n+1)x-cos(n-1)x]/(-2sinx)=- [cos(n+1)x+cosnx-cosx-1]/2sinx=右边等式得证[编辑本段]三角函数的诱导公式公式一：设α为任意角，终边相同的角的同一三角函数的值相等：sin（2kπ＋α）＝sinαcos（2kπ＋α）＝cosαtan（2kπ＋α）＝tanαcot（2kπ＋α）＝cotα公式二：设α为任意角，π+α的三角函数值与α的三角函数值之间的关系：sin（π＋α）＝－sinαcos（π＋α）＝－cosαtan（π＋α）＝tanαcot（π＋α）＝cotα公式三：任意角α与-α的三角函数值之间的关系：sin（－α）＝－sinαcos（－α）＝cosαtan（－α）＝－tanαcot（－α）＝－cotα公式四：利用公式二和公式三可以得到π-α与α的三角函数值之间的关系：sin（π－α）＝sinαcos（π－α）＝－cosαtan（π－α）＝－tanαcot（π－α）＝－cotα公式五：利用公式一和公式三可以得到2π-α与α的三角函数值之间的关系：sin（2π－α）＝－sinαcos（2π－α）＝cosαtan（2π－α）＝－tanαcot（2π－α）＝－cotα公式六：π/2±α及3π/2±α与α的三角函数值之间的关系：sin（π/2＋α）＝cosαcos（π/2＋α）＝－sinαtan（π/2＋α）＝－cotαcot（π/2＋α）＝－tanαsin（π/2－α）＝cosαcos（π/2－α）＝sinαtan（π/2－α）＝cotαcot（π/2－α）＝tanαsin（3π/2＋α）＝－cosαcos（3π/2＋α）＝sinαtan（3π/2＋α）＝－cotαcot（3π/2＋α）＝－tanαsin（3π/2－α）＝－cosαcos（3π/2－α）＝－sinαtan（3π/2－α）＝cotαcot（3π/2－α）＝tanα(以上k∈Z)[编辑本段]正余弦定理正弦定理是指在一个三角形中，各边和它所对的角的正弦的比相等，即a/sinA=b/sinB=c/sinC=2R ．余弦定理是指三角形中任何一边的平方等于其它两边的平方和减去这两边与它们夹角的余弦的积的2倍，即a^2=b^2+c^2-2bc cosA角A的对边于斜边的比叫做角A的正弦，记作sinA，即sinA=角A的对边/斜边斜边与邻边夹角asin=y/r无论y>x或y≤x无论a多大多小可以任意大小正弦的最大值为1 最小值为-[编辑本段]部分高等内容·高等代数中三角函数的指数表示(由泰勒级数易得)：sinx=[e^(ix)-e^(-ix)]/(2i)cosx=[e^(ix)+e^(-ix)]/2tanx=[e^(ix)-e^(-ix)]/[ie^(ix)+ie^(-ix)]泰勒展开有无穷级数，e^z=exp(z)＝1＋z/1！＋z^2/2！＋z^3/3！＋z^4/4！＋…＋z^n/n！＋…此时三角函数定义域已推广至整个复数集。

维基百科+k是一个整数.当x=+∞ N/A当x=-∞N/A 最大值(,∞) 最小值(,-∞)其他性质渐近线 N/A 根 无实根临界点 k π-π/2拐点 k π 不动点 0k 是一个整数.反正切反余切反正割反余割百度文库下载分别是正弦余弦正切余切正割余割角θ的所有三角函数(见:函数图形曲线)在平面直角坐标系xOy中，从点O引出一条射线OP，设旋转角为θ，设OP=r，P点的坐标为（x，y）有正弦函数sinθ=y/r余弦函数cosθ=x/r正切函数tanθ=y/x余切函数cotθ=x/y正割函数secθ=r/x余割函数cscθ=r/y（斜边为r，对边为y，邻边为x。

）以及两个不常用，已趋于被淘汰的函数：正矢函数versinθ =1-cosθ余矢函数coversθ =1-sinθ正弦（sin）:角α的对边比上斜边余弦（cos）:角α的邻边比上斜边正切（tan）:角α的对边比上邻边余切（cot）:角α的邻边比上对边正割（sec）:角α的斜边比上邻边余割（csc）:角α的斜边比上对边[编辑本段]同角三角函数间的基本关系式：·平方关系：sin^2α＋cos^2α＝11＋tan^2α＝sec^2α1＋cot^2α＝csc^2α·积的关系：sinα=tanα×cosαcosα=cotα×sinαtanα=sinα×secαcotα=cosα×cscαsecα=tanα×cscαcscα=secα×cotα·倒数关系：tanα ·cotα＝1sinα ·cscα＝1cosα ·secα＝1商的关系：sinα/cosα＝tanα＝secα/cscαcosα/sinα＝cotα＝cscα/secα直角三角形ABC中,角A的正弦值就等于角A的对边比斜边,余弦等于角A的邻边比斜边正切等于对边比邻边,·[1]三角函数恒等变形公式·两角和与差的三角函数：cos(α+β)=cosα·cosβ-sinα·sinβcos(α-β)=cosα·cosβ+sinα·sinβsin(α±β)=sinα·cosβ±cosα·sinβta n(α+β)=(tanα+tanβ)/(1-tanα·tanβ)tan(α-β)=(tanα-tanβ)/(1+tanα·tanβ)·三角和的三角函数：sin(α+β+γ)=sinα·cosβ·cosγ+cosα·sinβ·cosγ+cosα·cosβ·sinγ-sinα·sinβ·sinγcos(α+β+γ)=cosα·cosβ·cosγ-cosα·sinβ·sinγ-sinα·cosβ·sinγ-sinα·sinβ·cosγtan(α+β+γ)=(tanα+tanβ+tanγ-tanα·tanβ·tanγ)/(1-tanα·tanβ-tanβ·tanγ-tanγ·tanα)·辅助角公式：Asinα+Bcosα=(A²+B²)^(1/2)sin(α+arctan(B/A))，其中sint=B/(A²+B²)^(1/2)cost=A/(A²+B²)^(1/2)tant=B/AAsinα-Bcosα=(A²+B²)^(1/2)cos(α-t)，tant=A/B·倍角公式：sin(2α)=2sinα·cosα=2/(tanα+cotα)cos(2α)=cos²(α)-sin²(α)=2cos²(α)-1=1-2sin²(α)tan(2α)=2tanα/[1-tan²(α)]·三倍角公式：sin(3α)=3sinα-4sin³(α)=4sinα·sin(60+α)sin(60-α)cos(3α)=4cos³(α)-3cosα=4cosα·cos(60+α)cos(60-α)tan(3α)=tan a · tan(π/3+a)· tan(π/3-a)·半角公式：sin(α/2)=±√((1-cosα)/2)cos(α/2)=±√((1+cosα)/2)tan(α/2)=±√((1-cosα)/(1+cosα))=sinα/(1+cosα)=(1-cosα)/sinα·降幂公式sin²(α)=(1-cos(2α))/2=versin(2α)/2cos²(α)=(1+cos(2α))/2=covers(2α)/2tan²(α)=(1-cos(2α))/(1+cos(2α))·万能公式：sinα=2tan(α/2)/[1+tan²(α/2)]cosα=[1-tan²(α/2)]/[1+tan²(α/2)]tanα=2tan(α/2)/[1-tan²(α/2)]·积化和差公式：sinα·cosβ=(1/2)[sin(α+β)+sin(α-β)]cosα·sinβ=(1/2)[sin(α+β)-sin(α-β)]cosα·cosβ=(1/2)[cos(α+β)+cos(α-β)]sinα·sinβ=-(1/2)[cos(α+β)-cos(α-β)]·和差化积公式：sinα+sinβ=2sin[(α+β)/2]cos[(α-β)/2]sinα-sinβ=2cos[(α+β)/2]sin[(α-β)/2]cosα+cosβ=2cos[(α+β)/2]cos[(α-β)/2]cosα-cosβ=-2sin[(α+β)/2]sin[(α-β)/2]·推导公式tanα+cotα=2/sin2αtanα-cotα=-2cot2α1+cos2α=2cos²α1-cos2α=2sin²α1+sinα=(sinα/2+cosα/2)²·其他：sinα+sin(α+2π/n)+sin(α+2π*2/n)+sin(α+2π*3/n)+……+sin[α+2π*(n-1)/n]=0cosα+cos(α+2π/n)+cos(α+2π*2/n)+cos(α+2π*3/n)+……+cos[α+2π*(n-1)/n]=0 以及sin²(α)+sin²(α-2π/3)+sin²(α+2π/3)=3/2tanAtanBtan(A+B)+tanA+tanB-tan(A+B)=0cosx+cos2x+...+cosnx= [sin(n+1)x+sinnx-sinx]/2sinx证明：左边=2sinx(cosx+cos2x+...+cosnx)/2sinx=[sin2x-0+sin3x-sinx+sin4x-sin2x+...+ sinnx-sin(n-2)x+sin(n+1)x-sin(n-1)x]/2sinx （积化和差）=[sin(n+1)x+sinnx-sinx]/2sinx=右边等式得证sinx+sin2x+...+sinnx= - [cos(n+1)x+cosnx-cosx-1]/2sinx证明:左边=-2sinx[sinx+sin2x+...+sinnx]/(-2sinx)=[cos2x-cos0+cos3x-cosx+...+cosnx-cos(n-2)x+cos(n+1)x-cos(n-1)x]/(-2sinx)=- [cos(n+1)x+cosnx-cosx-1]/2sinx=右边等式得证三倍角公式推导sin3a=sin(2a+a)=sin2acosa+cos2asina=2sina(1-sin²a)+(1-2sin²a)sina=3sina-4sin³acos3a=cos(2a+a)=cos2acosa-sin2asina=(2cos²a-1)cosa-2(1-sin²a)cosa=4cos³a-3cosasin3a=3sina-4sin³a=4sina(3/4-sin²a)=4sina[(√3/2)²-sin²a]=4sina(sin²60°-sin²a)=4sina(sin60°+sina)(sin60°-sina)=4sina*2sin[(60+a)/2]cos[(60°-a)/2]*2sin[(60°-a)/2]cos[(60°+a)/2]=4sinasin(60°+a)sin(60°-a)cos3a=4cos³a-3cosa=4cosa(cos²a-3/4)=4cosa[cos²a-(√3/2)²]=4cosa(cos²a-cos²30°)=4cosa(cosa+cos30°)(cosa-cos30°)=4cosa*2cos[(a+30°)/2]cos[(a-30°)/2]*{-2sin[(a+30°)/2]sin[(a-30°)/2]}=-4cosasin(a+30°)sin(a-30°)=-4cosasin[90°-(60°-a)]sin[-90°+(60°+a)]=-4cosacos(60°-a)[-cos(60°+a)]=4cosacos(60°-a)cos(60°+a)上述两式相比可得tan3a=tanatan(60°-a)tan(60°+a)[编辑本段]三角函数的诱导公式公式一：设α为任意角，终边相同的角的同一三角函数的值相等：sin（2kπ＋α）＝sinαcos（2kπ＋α）＝cosαtan（2kπ＋α）＝tanαcot（2kπ＋α）＝cotα公式二：设α为任意角，π+α的三角函数值与α的三角函数值之间的关系：sin（π＋α）＝－sinαcos（π＋α）＝－cosαtan（π＋α）＝tanαcot（π＋α）＝cotα公式三：任意角α与-α的三角函数值之间的关系：sin（－α）＝－sinαcos（－α）＝cosαtan（－α）＝－tanαcot（－α）＝－cotα公式四：利用公式二和公式三可以得到π-α与α的三角函数值之间的关系：sin（π－α）＝sinαcos（π－α）＝－cosαtan（π－α）＝－tanαcot（π－α）＝－cotα公式五：利用公式一和公式三可以得到2π-α与α的三角函数值之间的关系：sin（2π－α）＝－sinαcos（2π－α）＝cosαtan（2π－α）＝－tanαcot（2π－α）＝－cotα公式六：π/2±α及3π/2±α与α的三角函数值之间的关系：sin（π/2＋α）＝cosαcos（π/2＋α）＝－sinαtan（π/2＋α）＝－cotαcot（π/2＋α）＝－tanαsin（π/2－α）＝cosαcos（π/2－α）＝sinαtan（π/2－α）＝cotαcot（π/2－α）＝tanαsin（3π/2＋α）＝－cosαcos（3π/2＋α）＝sinαtan（3π/2＋α）＝－cotαcot（3π/2＋α）＝－tanαsin（3π/2－α）＝－cosαcos（3π/2－α）＝－sinαtan（3π/2－α）＝cotαcot（3π/2－α）＝tanα(以上k∈Z)定名法则90°的奇数倍+α的三角函数，其绝对值与α三角函数的绝对值互为余函数。

数学三⾓函数正弦、余弦、正割、余割、正切、余切的概念深⼊解读进⼊⾼中后，同学们都要开始学习三⾓函数的知识了。

三⾓函数总共分为六个：
正弦（sin）、余弦（cos）；
正切（tan）、余切（cot）；
正割（sec）、余割（cosec）。

很多学⽣学完后的感觉就是⼀个字——绕。

这六个三⾓函数的彼此关系确实太绕了。

今天【⼗次⽼师】就为⼤家深扒⼀下它们。

名字来源
正⾓和余⾓
1. 正和余的命名原则：
在单位圆中，⾓AOB为正⾓；⾓BOE为余⾓。

这两个⾓互余。

劣弧AB为正⾓AOB所对的
弧，我们称为正弧，同理余⾓BOE所对的弧为余弧。

2. 弦、切、割的命名原则：
弦的理解
连接两个定点线段
弦的理解
切的理解
沿着边缘切
割线的理解
割开分割的含义
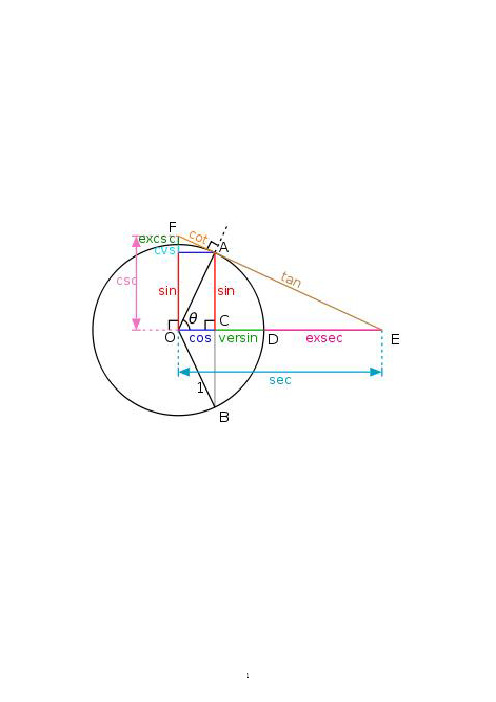
在单位圆中表⽰正余+弦切割
正弦+正切+正割
余弦+余割+余切
由这⼏个长度可以分别构造出两个三⾓形，我称呼他们为正⾓三⾓形和余⾓三⾓形。

如图：
正⾓三⾓形和余⾓三⾓形
这个两个三⾓形彼此相似。

有相似性可推出：
半径（1）：余切 =正切：半径（1）【正切余切互为倒数】由勾股定理可推出：
正切的平⽅+半径（1）的平⽅ = 正割的平⽅
余切的平⽅+半径（1）的平⽅ = 余割的平⽅
三⾓函数⼤⼀统图
本⽂图形采⽤GeoGebra绘制
编写不宜，希望各位看官们，随⼿点个赞。

高三三角函数高三三角函数是高中数学中的一门重要课程，它是数学中的一种基础工具，也是物理、化学等学科中不可或缺的数学工具。

三角函数是指正弦函数、余弦函数、正切函数、余切函数、正割函数、余割函数这六种函数，它们是由角度的变化而产生的一系列函数。

在高三三角函数中，我们需要掌握三角函数的定义、性质、图像、解三角形、三角函数的应用等知识。

首先，我们需要了解三角函数的定义，正弦函数、余弦函数、正切函数、余切函数、正割函数、余割函数的定义分别为：sinθ=y/r，cosθ=x/r，tanθ=y/x，cotθ=x/y，secθ=r/x，cscθ=r/y。

其中，θ为角度，x、y、r分别为直角三角形中的对边、邻边和斜边。

我们需要掌握三角函数的性质，如周期性、奇偶性、单调性、界值、反函数等。

例如，正弦函数和余弦函数的周期都是2π，正切函数和余切函数的周期都是π，正割函数和余割函数的周期都是π。

正弦函数、正切函数、正割函数是奇函数，余弦函数、余切函数、余割函数是偶函数。

正弦函数、余弦函数、正切函数、余切函数在一个周期内都是单调的，正割函数、余割函数在一个周期内有两个单调区间。

正弦函数、余弦函数的最大值为1，最小值为-1，正切函数、余切函数没有最大值和最小值，正割函数、余割函数的最小值为1，最大值为正无穷。

我们还需要掌握三角函数的图像，正弦函数、余弦函数的图像是一条波浪线，正切函数、余切函数的图像是一条直线，正割函数、余割函数的图像是两条平行的直线。

通过掌握三角函数的图像，我们可以更好地理解三角函数的性质。

我们需要掌握三角函数的应用，如解三角形、求极值、求导数、解方程等。

三角函数在物理、化学等学科中有广泛的应用，如在力学中，三角函数可以用来描述物体的运动状态；在化学中，三角函数可以用来描述分子的振动状态。

高三三角函数是高中数学中的一门重要课程，它是数学中的一种基础工具，也是物理、化学等学科中不可或缺的数学工具。

通过学习三角函数，我们可以更好地理解数学中的各种概念和方法，为我们今后的学习和工作打下坚实的数学基础。

三角函数余切,正割,余割和差角,半角,二倍角等公式三角函数余切，正割，余割和差角，半角，二倍角等公式是在数学函数中十分重要的一部分，也是很多数学领域中研究和应用的一块意义重大的基石。

三角函数曲线中存在着余切，正割，余割和差角，半角，二倍角等几种不同的公式，今天我们就来聊聊这三种公式的概念，并讨论它们的区别及应用。

首先我们来了解一下三角函数余切公式。

余切，也叫余切函数，是一种三角函数。

它是对三角函数y=sinθ在各个θ值处取倒数后，得到一个新的函数，即Cotθ。

余切函数也可以写成y=1/sinθ。

由此可见，余切和正弦函数正好相反，因此，余切也被称为正弦的“倒数函数”。

接下来介绍的是三角函数正割公式。

正割函数，也称为正割函数，是三角函数当中的一种，以正割函数表示为y=cosθ。

正割函数是从余弦函数中求倒数得到的函数，因此又称正弦的“倒数函数”。

最后我们来介绍余割与差角，半角，二倍角等公式。

余割函数是一种三角函数，其中余割函数由余切函数和正割函数的乘积得到，表示为y=Cotθ * tanθ=sinθ/cosθ。

差角是指两个给定角（比如θ1和θ2）之间的角度差值。

差角公式可表示为θ=θ2-θ1。

半角是指一个给定角的一半，即θ2=θ1/2，表示为θ2=θ1/2。

而二倍角则是指一个给定角的两倍，即θ2=θ1*2，表示为θ2=θ1*2。

总结一下，以上三角函数余切，正割，余割和差角，半角，二倍角等公式的概念的区别和应用如下：余切：是在三角函数曲线中以余切函数表示的函数，它是对三角函数y=sinθ在各个θ值处取倒数后，得到一个新的函数，即Cotθ。

正割：是一种三角函数，以正割函数表示为y=cosθ，是从余弦函数中求倒数得到的函数，也叫正弦的“倒数函数”。

余割：是一种三角函数，由余切函数和正割函数的乘积得到，表示为y=Cotθ * tanθ=sinθ/cosθ。

差角：是指两个给定角（比如θ1和θ2）之间的角度差值，公式可表示为θ=θ2-θ1。

三角函数的运算公式三角函数是数学中的一种重要函数，常用于解决与角度和三角形相关的问题。

它们由正弦函数、余弦函数、正切函数、余切函数、正割函数和余割函数组成。

这些函数之间有许多运算公式，将在下文中详细介绍。

1.正弦函数的运算公式：- 正弦函数的周期性质：sin(x + 2πn) = sin(x)，其中n为整数。

- 正弦函数的奇偶性质：sin(-x) = -sin(x)。

-正弦函数的和差公式：- sin(x ± y) = sin(x)cos(y) ± cos(x)sin(y)-正弦函数的倍角公式：- sin(2x) = 2sin(x)cos(x)-正弦函数的半角公式：- sin(x/2) = ±√[(1 - cos(x))/2]-正弦函数的倒数公式：- csc(x) = 1/sin(x)2.余弦函数的运算公式：- 余弦函数的周期性质：cos(x + 2πn) = cos(x)，其中n为整数。

- 余弦函数的奇偶性质：cos(-x) = cos(x)。

-余弦函数的和差公式：- cos(x ± y) = cos(x)cos(y) ∓ sin(x)sin(y)-余弦函数的倍角公式：- cos(2x) = cos²(x) - sin²(x) = 2cos²(x) - 1 = 1 - 2sin²(x) -余弦函数的半角公式：- cos(x/2) = ±√[(1 + cos(x))/2]-余弦函数的倒数公式：- sec(x) = 1/cos(x)3.正切函数的运算公式：- 正切函数的周期性质：tan(x + πn) = tan(x)，其中n为整数。

- 正切函数的奇偶性质：tan(-x) = -tan(x)。

-正切函数的和差公式：- tan(x ± y) = (tan(x) ± tan(y))/(1 ∓ tan(x)tan(y))-正切函数的倍角公式：- tan(2x) = (2tan(x))/(1 - tan²(x))-正切函数的半角公式：- tan(x/2) = ±√[(1 - cos(x))/(1 + cos(x))]-正切函数的倒数公式：- cot(x) = 1/tan(x)4.余切函数的运算公式：- 余切函数的周期性质：cot(x + πn) = cot(x)，其中n为整数。

正弦余弦正切余切正割余割的关系下载温馨提示:该文档是我店铺精心编制而成，希望大家下载以后，能够帮助大家解决实际的问题。

文档下载后可定制随意修改，请根据实际需要进行相应的调整和使用，谢谢!并且，本店铺为大家提供各种各样类型的实用资料，如教育随笔、日记赏析、句子摘抄、古诗大全、经典美文、话题作文、工作总结、词语解析、文案摘录、其他资料等等，如想了解不同资料格式和写法，敬请关注!Download tips: This document is carefully compiled by theeditor.I hope that after you download them,they can help yousolve practical problems. The document can be customized andmodified after downloading,please adjust and use it according toactual needs, thank you!In addition, our shop provides you with various types ofpractical materials,such as educational essays, diaryappreciation,sentence excerpts,ancient poems,classic articles,topic composition,work summary,word parsing,copy excerpts,other materials and so on,want to know different data formats andwriting methods,please pay attention!三角函数的紧密联系：正弦、余弦、正切、余切与正割、余割的关系在数学的世界里，三角函数是一组重要的函数，它们在几何学、物理学、工程学等多个领域有着广泛的应用。