(完整版)全等三角形经典模型总结

全等三角形八大基本模型
（原创实用版）
目录
1.全等三角形的定义与性质
2.全等三角形的八大基本模型
1.手拉手模型
2.一线三垂直模型
3.一线三等角模型
4.等腰三角形中边边角模型
5.背对背模型
6.半角旋转模型
7.角分线模型
8.正方形手拉手模型
正文
全等三角形是指两个三角形的对应边和对应角分别相等的三角形。

在解决全等三角形问题时，我们需要了解全等三角形的定义和性质，以及掌握一些常用的模型。

本文将介绍全等三角形的八大基本模型，希望能帮助大家更好地理解和解决全等三角形问题。

1.手拉手模型：两个三角形通过一个公共边，并且这个公共边的两个端点分别与另外两个三角形的顶点相连。

2.一线三垂直模型：两个三角形的一组对应边互相平行，且另外两组对应边互相垂直。

3.一线三等角模型：两个三角形的一组对应边互相平行，且另外两组对应角相等。

4.等腰三角形中边边角模型：两个等腰三角形，其中一个等腰三角形的底边与另一个等腰三角形的腰相等，且两个等腰三角形的底角相等。

5.背对背模型：两个三角形的一组对应边互相垂直，且另外一组对应边互相平行。

6.半角旋转模型：一个三角形通过某个顶点旋转 180 度后与另一个三角形重合。

7.角分线模型：两个三角形的一组对应角相等，且另一组对应边的延长线相交于一点，这个点将延长线分成的两段长度相等。

8.正方形手拉手模型：两个正方形，其中一个正方形的一边与另一个正方形的一边相连，另外两个正方形的边也分别相连。

以上就是全等三角形的八大基本模型，这些模型在解决全等三角形问题时非常实用。

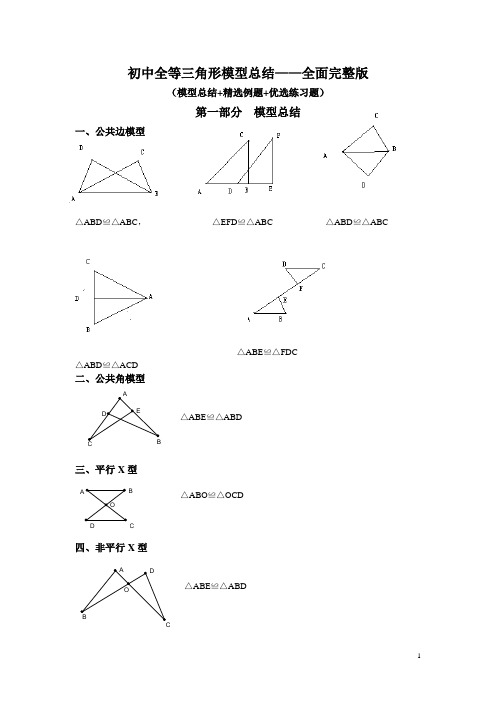
初中全等三角形模型总结——全面完整版（模型总结+精选例题+优选练习题）第一部分 模型总结一、公共边模型△ABD ≌△ABC ， △EFD ≌△ABC △ABD ≌△ABC△ABE ≌△FDC △ABD ≌△ACD二、公共角模型△ABE ≌△ABD三、平行X 型△ABO ≌△OCD四、非平行X 型△ABE ≌△ABDA B EDOA BDCO A BD五、母子等腰三角形△ABD ≌△AEC ，△ABE ≌△ACD六、旋转模型图1△ ABC ≌△AB`C第二部分 精选例题例1．如图，已知AB ∥CD ，AD ∥BC ，F 在DC 的延长线上，AM =CF ，FM 交DA 的延长线上于E .交BC 于N,求证:AE=CN.思路分析:欲证AE=CN.看它们在哪两个三角形中, 设法证这两个三角形全等即可.结合图形可发现 △AME ≌△FCN 可证.题设告知AM=CF,AD ∥BC,AB ∥CD.由两平行条件, 可找两对角相等.∵∠1=∠2(对顶角相等)∴∠2=∠E(等量代换)∴AE=CN (全等三角形的对应边相等)例2.△ABC 中，∠ACB =90°，AC =BC ，过C 的一条直线CE ⊥AE 于E ，BD ⊥CE 的延长线于D ，求证：AE =BD +DE .思路分析：从本例的结论知是求线段和的问题， 由此入手，很难找到突破口.此时可迅速调整思维角 度,可仔细观察图形,正确的图形是证题的“向导”,由 此可发现△ACE 与△CBD 好像(猜测)全等.那么AE =CD =CE +DE .又BD =CE .那么,此时已水落石出.B CAE D C 'B'AB C 'B 'BAAC=BC（已知）∠1=∠3 （已证）∠AEC=∠CDB（已证）∴△ACE≌△CBD（AAS）∴BD=CE，AE=CD（全等三角形的对应边相等）∵AE=CE=CE+DE∴AE=BD+DE（等量代换）例3．如图，AD是△ABC的中线，DE，DF分别平分∠ADB和∠ADC，连接EF，求证：EF<BE+CF. 定对象：△ABC定角度：三角形全等分析:由结论EF<BE+CF很容易与定理“三角形两边之和大于第三边”联系在一块，观察图形，BE，CF，EF条件分散，不在一个三角形中，必须设法（平移，旋转，翻转等）把三者集中在一个三角形中，是打开本例思路的关键.由角的平分线这一线索,可将△BDE沿角平分线翻转180°,即B点落在AD的点B'上(如图)(也就是在DA上截取DB＇=BD),连结EB＇,B＇F,此时△BDE与△B＇DE完全重合,所以△BDE≌△B＇DE(两个三角形能够完全重合就是全等三角形,所以BE=B＇E(全等三角形的对应边相等).在△EFB＇中,EF<B＇E+B＇F(三角形的两边之和大于第三边).∴EF<BE+CF(等量代换).例4如图，已知CD⊥AB于D，BE⊥AC于E，△ABE≌△ACD，∠C= 20°，AB=10，AD= 4，G为AB延长线上一点．求∠EBG的度数和CE的长．定对象：如图定角度：三角形全等分析：(1)图中可分解出四组基本图形：有公共角的Rt△ACD和Rt△ABE；△ABE≌△ACD，△ABE的外角∠EBG或∠ABE的邻补角∠EBG．例5已知：如图，△ABC≌△ADE，BC的延长线交DA于F，交DE于G，∠ACB=105°，∠CAD＝10°，∠D=25°．求∠EAC，∠DFB，∠DGB的度数．例6.在△ABC 中，∠C ＝90°，AC ＝BC ，AD 是∠BAC 的平分线，DE ⊥AB ，垂足为E ，若AB ＝20 cm ，则△DBE 的周长等于多少？分析：对象：△DBE 的周长 角度：（1）BD ，DE ，BE 的长解： 因为DE ⊥AB ，所以AED ACD ∠=∠因为AD 是∠BAC 的平分线，所以EAD CAD ∠=∠又因为AD 为公共边 所以AED ACD ≅ 则AE=AC DE=DC 所以△DBE 的周长=BE+DE+BD=AB-AE+BC=20例7如图13—3—8所示，已知在△ABC 中，AD 是∠BAC 的平分线，DE ⊥AB 于E ，DF ⊥AC 于F ．求证：EF ⊥AD ．分析：对象：△ABC 角度：（1）AD 是∠BAC 的平分线，（2）DE ⊥AB 于E ，DF ⊥AC 于F 证明：因为DE ⊥AB 于E ，DF ⊥AC 于F ，所以090AED AFD ∠=∠= 又因为AD 是∠BAC 的平分线，所以EAD FAD ∠=∠由于AD 是公共边 所以AED AFD ≅ 则AE=AF 因为AD 是∠BAC 的平分线 所以EF ⊥AD 。

数学全等三角形五大模型及必要步骤
一、等积变换模型
1、等底等高的两个三角形面积相等.
2、两个三角形高相等,面积比等于它们的底之比.
3、两个三角形底相等,面积比等于它的的高之比.
二、共角定理模型
两个三角形中有一个角相等或互补,这两个三角形叫做共角三角形.
共角三角形的面积比等到于对应角（相等角或互补角）两夹边的乘积之比.
三、蝴蝶定理模型
（说明：任意四边形与四边形、长方形、梯形,连接对角线所成四部的比例关系是一样的.）四、相似三角形模型
相似三角形：是形状相同,但大小不同的三角形叫相似三角形.
相似三角形的一切对应线段的长度成比例,并且这个比例等于它们的相似比.
相似三角形的面积比等于它们相似比的平方.
五、燕尾定理模型
不多说了,应该知道吧。

全等三角形八大模型归纳全等三角形是初中数学中重要的概念之一，它是指两个三角形的对应边相等且对应角相等。

全等三角形具有许多性质和特点，可以归纳为八大模型，分别是SSS、SAS、ASA、AAS、HL、LLL、LLA、LAL。

下面将分别介绍这八种模型的特点和应用。

第一种模型是SSS，即三边全等。

当两个三角形的三条边分别相等时，这两个三角形就是全等的。

这种模型在实际生活中的应用非常广泛，比如在建筑、工程设计中，需要测量房屋的各个边长是否相等，以确保建筑物的稳定性和均衡性。

第二种模型是SAS，即两边夹角边全等。

当两个三角形的两边和夹角分别相等时，这两个三角形就是全等的。

这种模型常常用于证明两个三角形全等的情况，可以通过辅助线的引入来简化证明过程。

第三种模型是ASA，即两角边角全等。

当两个三角形的两个角和夹边分别相等时，这两个三角形就是全等的。

这种模型在解题过程中也经常用到，特别是在证明题中，可以根据已知条件找到相等的角和边，从而得出结论。

第四种模型是AAS，即两角边角全等。

当两个三角形的两个角和一边分别相等时，这两个三角形也是全等的。

这种情况在证明过程中比较常见，可以通过找到两个角和一边相等来得出结论。

第五种模型是HL，即斜边和直角边全等。

当两个直角三角形的斜边和一个直角边分别相等时，这两个三角形就是全等的。

这种情况在解决直角三角形的问题时经常用到，可以利用勾股定理和全等三角形的性质来求解。

第六种模型是LLL，即三边全等。

这种模型和SSS模型类似，只不过LLL模型更加具体，强调了三个边全部相等的情况。

在实际问题中，可以通过测量三角形的三边长度来判断两个三角形是否全等。

第七种模型是LLA，即两边和一个角全等。

当两个三角形的两个边和一个非夹角的角相等时，这两个三角形是全等的。

这种情况在解题过程中也会经常遇到，可以通过找到两个边和一个非夹角的角相等来证明两个三角形全等。

第八种模型是LAL，即一边和两个角全等。

当两个三角形的一条边和两个角分别相等时，这两个三角形也是全等的。

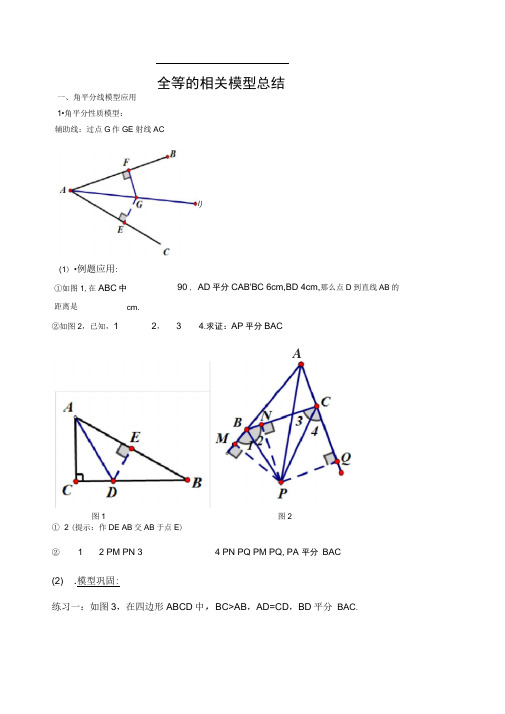
全等的相关模型总结一、角平分线模型应用 1•角平分性质模型：②如图2，已知，1 2， 3 4.求证：AP 平分BACA① 2 (提示：作DE AB 交AB 于点E )②1 2 PM PN 3 4 PN PQ PM PQ, PA 平分 BAC(2) .模型巩固:练习一：如图3，在四边形ABCD 中，BC>AB ，AD=CD ，BD 平分 BAC .①如图1,在ABC 中 距离是90°, AD 平分CAB'BC 6cm,BD 4cm,那么点D 到直线AB 的cm.I)(1) •例题应用: 辅助线：过点G 作GE 射线AC图1图2•求证： A C 180练习二：已知如图4,四边形ABCD中，B D 1800,BC CD•求证：AC平分BAD.练习三：如图5 Rt ABC中，ACB 90 , CD AB,垂足为D , AF平分CAB,交CD于点E 交CB于点F.(1)求证：CE=CF.(2)将图5中的△ ADE沿AB向右平移到ADE的位置，使点E落在BC边上，其他条件不变，如图6所示，是猜想：BE于CF又怎样的数量关系？请证明你的结论图5 图6练习四：如图7，/ A 90，AD // BC，P是AB的中点，PD平分/ ADC求证：CP 平分/ DCB图7练习五：如图 8, AB> AC / A 的平分线与 BC 的垂直平分线相交于 D,自D 作DE L AB, DF 丄AC,垂足 分别为E , F .求证：BE=CF图8练习六：如图9所示，在△ ABC 中，BC 边的垂直平分线 DF 交厶BAC 的外角平分线 AD 于点D , F 为垂足，DE 丄AB 于E ,并且 AB>AC 。

求证：BE — AC=AE 。

练习七： 如图10, D 、E 、F 分别是△ ABC 的三边上的点， CE=BF ，且△ DCE 的面积与厶 DBF 的面 积相等，求证：AD 平分/ BAC 。

全等三角形相關模型總結一、角平分線模型(一）角平分線の性質模型輔助線：過點G作GE⊥射線ACA、例題1、如圖，在△ABC中，∠C=90°，AD平分∠CAB，BC=6cm，BD=4cm，那麼點D到直線AB の距離是cm.2、如圖，已知，∠1＝∠2，∠3＝∠4，求證：AP平分∠BAC.B、模型鞏固1、如圖，在四邊形ABCD中，BC＞AB，AD＝CD，BD平分∠ABC，求證：∠A＋∠C＝180°.（二）角平分線＋垂線，等腰三角形必呈現A、例題輔助線：延長ED交射線OB於F 輔助線：過點E作EF∥射線OB 例1、如圖，在△ABC中，∠ABC＝3∠C，AD是∠BACの平分線，BE⊥AD於F .求證：1()2BE AC AB=-.例2、如圖，在△ABC中，∠BACの角平分線AD交BC於點D，且AB＝AD，作CM⊥AD交ADの延長線於M. 求證：1()2AM AB AC=+.（三）角分線，分兩邊，對稱全等要記全兩個圖形飛輔助線都是在射線ON上取點B，使OB＝OA，從而使△OAC≌△OBC .A、例題1、如圖，在△ABC中，∠BAC=60°，∠C=40°，AP平分∠BAC交BC於P，BQ平分∠ABC 交AC於Q，求證：AB＋BP＝BQ＋AQ .2、如圖，在△ABC中，AD是∠BACの外角平分線，P是AD上異於點Aの任意一點，試比較PB＋PC與AB＋ACの大小，並說明理由.B、模型鞏固1、在△ABC中，AB＞AC，AD是∠BACの平分線，P是線段AD上任意一點（不與A重合）.求證：AB－AC＞PB－PC .2、如圖，△ABC中，AB＝AC，∠A＝100°，∠Bの平分線交AC於D，求證：AD＋BD＝BC .3、如圖，△ABC中，BC＝AC，∠C＝90°，∠Aの平分線交BC於D，求證：AC＋CD＝AB .二、等腰直角三角形模型（一）旋轉中心為直角頂點，在斜邊上任取一點の旋轉全等：操作過程：（1）將△ABD逆時針旋轉90°，得△ACM ≌△ABD，從而推出△ADM為等腰直角三角形.（2）輔助線作法：過點C作MC⊥BC，使CM＝BD，連結AM.（二）旋轉中心為斜邊中點，動點在兩直角邊上滾動の旋轉全等：操作過程：連結AD.（1）使BF＝AE（或AF＝CE），導出△BDF ≌△ADE.（2）使∠EDF＋∠BAC＝180°，導出△BDF ≌△ADE.A、例題1、如圖，在等腰直角△ABC中，∠BAC＝90°，點M、N在斜邊BC上滑動，且∠MAN＝45°，試探究BM、MN、CN之間の數量關係.2、兩個全等の含有30°，60°角の直角三角板ADE和ABC，按如圖所示放置，E、A、C三點在一條直線上，連接BD，取BDの中點M，連接ME、MC.試判斷△EMCの形狀，並證明你の結論.B、模型鞏固1、已知，如圖所示，Rt△ABC中，AB＝AC，∠BAC＝90°，O為BC中點，若M、N分別線上段AC、AB上移動，且在移動中保持AN＝CM.（1）試判斷△OMNの形狀，並證明你の結論.（2）當M、N分別線上段AC、AB上移動時，四邊形AMONの面積如何變化？2、在正方形ABCD中，BE＝3，EF＝5，DF＝4，求∠BAE＋∠DCF為多少度.（三）構造等腰直角三角形（1）利用以上（一）和（二）都可以構造等腰直角三角形（略）；（2）利用平移、對稱和絃圖也可以構造等腰直角三角形.（四）將等腰直角三角形補全為正方形，如下圖：A、例題應用1、如圖，在等腰直角△ABC中，AC＝BC，∠ACB＝90°，P為三角形ABC內部一點，滿足PB＝PC，AP＝AC，求證：∠BCP＝15°.三、三垂直模型（弦圖模型）A、例題已知：如圖所示，在△ABC中，AB＝AC，∠BAC＝90°，D為AC中點，AF⊥BD於點E，交BC於F，連接DF .求證：∠ADB＝∠CDF .變式1、已知：如圖所示，在△ABC中，AB＝AC，AM＝CN，AF⊥BM於E，交BC於F，連接NF .求證：（1）∠AMB＝∠CNF；（2）BM＝AF＋FN .變式2、在變式1の基礎上，其他條件不變，只是將BM和FN分別延長交於點P，求證：（1）PM＝PN；（2）PB＝PF＋AF .Fpg四、手拉手模型1、△ABE和△ACF均為等邊三角形結論：（1）△ABF≌△AEC .（2）∠BOE＝∠BAE＝60°.（3）OA平分∠EOF .（四點共圓證）拓展：△ABC和△CDE均為等邊三角形結論：（1）AD＝BE；（2）∠ACB＝∠AOB；（3）△PCQ為等邊三角形；（4）PQ∥AE；（5）AP＝BQ；（6）CO平分∠AOE；（四點共圓證）（7）OA＝OB＋OC；（8）OE＝OC＋OD .（（7），（8）需構造等邊三角形證明）Fpg 例、如圖①，點M為銳角三角形ABC內任意一點，連接AM、BM、CM．以AB為一邊向外作等邊三角形△ABE，將BM繞點B逆時針旋轉60°得到BN，連接EN．（1）求證：△AMB≌△ENB；（2）若AM+BM+CMの值最小，則稱點M為△ABCの費爾馬點．若點M為△ABCの費爾馬點，試求此時∠AMB、∠BMC、∠CMAの度數；（3）小翔受以上啟發，得到一個作銳角三角形費爾馬點の簡便方法：如圖②，分別以△ABC のAB、AC為一邊向外作等邊△ABE和等邊△ACF，連接CE、BF，設交點為M，則點M 即為△ABCの費爾馬點．試說明這種作法の依據．2、△ABD 和△ACE 均為等腰直角三角形結論：（1）BE ＝CD ；（2）BE ⊥CD .3、四邊形ABEF 和四邊形ACHD 均為正方形結論：（1）BD ＝CF ；（2）BD ⊥CF .變式1、四邊形ABEF 和四邊形ACHD 均為正方形，AS ⊥BC 交FD 於T ，求證：（1）T 為FD 中點；（2）ABC ADF SS .變式2、四邊形ABEF和四邊形ACHD均為正方形，T為FD中點，TA交BC於S，求證：AS⊥BC .4、如圖，以△ABCの邊AB、AC為邊構造正多邊形時，總有：360 12180n︒∠=∠=︒-五、半角模型條件：1,+=1802αββθβ=︒且，兩邊相等.思路：1、旋轉輔助線：①延長CD到E，使ED=BM，連AE或延長CB到F，使FB=DN，連AF②將△ADN繞點A順時針旋轉90°得△ABF，注意：旋轉需證F、B、M三點共線結論：（1）MN＝BM＋DN；（2）=2CMNC AB；（3）AM、AN分別平分∠BMN、∠MND .2、翻折（對稱）輔助線：①作AP⊥MN交MN於點P②將△ADN、△ABM分別沿AN、AM翻折，但一定要證明M、P、N三點共線 .A、例題例1、在正方形ABCD中，若M、N分別在邊BC、CD上移動，且滿足MN＝BM＋DN，求證：（1）∠MAN＝45°；C AB；（2）=2CMN（3）AM、AN分別平分∠BMN和∠DNM .變式：在正方形ABCD中，已知∠MAN＝45°，若M、N分別在邊CB、DCの延長線上移動，AH⊥MN，垂足為H，（1）試探究線段MN、BM、DN之間の數量關係；（2）求證：AB＝AH例2、在四邊形ABCD中，∠B＋∠D＝180°，AB＝AD，若E、F分別為邊BC、CD上の點，且滿足EF＝BE＋DF，求證：12EAF BAD ∠=∠.變式：在四邊形ABCD中，∠B＝90°，∠D＝90°，AB＝AD，若E、F分別為邊BC、CD上の點，且12EAF BAD∠=∠，求證：EF＝BE＋DF .。

1初中数学几何模型【模型1】倍长1、 倍长中线；2、倍长类中线；3、中点遇平行延长相交EABCFABC---------------------------------------------------------------------------------------------------------------------- 【模型2】遇多个中点，构造中位线1、 直接连接中点；2、连对角线取中点再相连【例1】在菱形ABCD 和正三角形BEF 中，∠ABC =60°，G 是DF 的中点，连接GC 、GE ． （1）如图1，当点E 在BC 边上时，若AB =10，BF =4，求GE 的长；（2）如图2，当点F 在AB 的延长线上时，线段GC 、GE 有怎样的数量和位置关系，写出你的猜想；并给予证明；（3）如图3，当点F 在CB 的延长线上时，(2)问中关系还成立吗？写出你的猜想，并给予证明.图1DFD【例2】如图，在菱形ABCD 中，点E 、F 分别是BC 、CD 上一点，连接DE 、EF ，且AE =AF ，BAF DAE ∠=∠． (1)求证：CE =CF ；(2)若︒=∠120ABC ，点G 是线段AF 的中点，连接DG ，EG ．求证：DG 上GE ．2E CODECOD O C【例3】如图，在四边形ABCD 中，AB =CD ，E 、F 分别为BC 、AD 中点，BA 交EF 延长线于G ，CD 交EF 于H ．求证：∠BGE =∠CHE ．HGEFA BDC【模型1】构造轴对称【模型2】角平分线遇平行构造等腰三角形---------------------------------------------------------------------------------------------------------------------- 【例4】如图，平行四边形ABCD 中，AE 平分∠BAD 交BC 边于E ，EF ⊥AE 交CD 边于F ，交AD 边于H ，延长BA 到点G ，使AG =CF ，连接GF ．若BC =7，DF =3，EH =3AE ，则GF 的长为.HGFEADBC【条件】OA OB OC OD AOB COD ==∠=∠，，【结论】OAC OBD ≅；AEB OAB COD ∠=∠=∠（即都是旋转角）；OE AED ∠平分；3CDA B EEFEBDAC---------------------------------------------------------------------------------------------------------------------- 【例5】如图，正方形ABCD 的边长为6，点O 是对角线AC 、BD 的交点，点E 在CD 上，且DE =2CE ，过点C 作CF ⊥BE ，垂足为F ，连接OF ，则OF 的长为 .【例6】如图，ABC 中，90BAC ︒∠=，AB =AC ，AD ⊥BC 于点D ，点E 在AC 边上，连结BE ，AG ⊥BE 于F ，交BC 于点G ，求DFG ∠GFD CBAE【例7】如图，在边长为62ABCD 中，E 是AB 边上一点，G 是AD 延长线上一点，BE ＝DG ，连接EG ，CF ⊥EG 于点H ，交AD 于点F ，连接CE 、BH 。

全等的相关模型总结一、角平分线模型应用1.角平分性质模型：辅助线：过点G 作 GE射线AC（1） .例题应用：①如图 1，在ABC中，C900， AD 平分 CAB , BC 6cm, BD 4cm,那么点 D 到直线 AB 的距离是cm.②如图 2，已知，1 2 ，34 .求证： AP平分 BAC .图 1图2① 2（提示：作 DE AB 交 AB 于点 E ）②12 ， PM PN ，3 4 ， PN PQ ， PM PQ, PA平分 BAC .(2).模型巩固：练习一：如图3，在四边形 ABCD 中， BC>AB ， AD=CD ，BD 平分BAC ..求证：A C180图3练习二：已知如图4，四边形 ABCD 中，B D 1800 , BC CD.求证： AC 平分BAD .图 4练习三：如图5，Rt ABC 中， ACB900， CD AB, 垂足为 D ， AF 平分CAB ,交 CD 于点 E ，交 CB 于点 F.(1)求证： CE=CF.(2)将图 5 中的△ ADE 沿 AB 向右平移到A' D ' E '的位置，使点 E'落在BC边上，其他条件不变，如图 6 所示，是猜想：BE'于 CF 又怎样的数量关系？请证明你的结论.图 5图6练习四：如图7，∠ A90 ， AD ∥ BC ， P 是 AB的中点， PD平分∠ ADC．求证： CP平分∠ DCB．A D214E3PB C图 7练习五：如图8，AB＞ AC，∠ A 的平分线与 BC的垂直平分线相交于D，自 D 作 DE⊥ AB，DF⊥ AC，垂足分别为 E， F．求证： BE=CF．图 8练习六：如图9 所示，在△ ABC 中， BC 边的垂直平分线DF 交△ BAC 的外角平分线AD 于点 D， F 为垂足， DE ⊥AB 于 E，并且 AB>AC 。

求证： BE－ AC=AE 。

全等三角形相关模型总结一、角平分线模型(一）角平分线的性质模型辅助线：（双垂直）过点G作GE⊥射线AC1、如图，已知，∠1＝∠2，∠3＝∠4，求证：AP平分∠BAC.2、如图，在四边形ABCD中，BC＞AB，AD＝CD，BD平分∠ABC，求证：∠A＋∠C ＝180°.（二）角平分线＋垂线，等腰三角形必呈现辅助线1：延长ED交射线OB于F辅助线2：过点E作EF∥射线OB 1、如图，在△ABC中，∠BAC的角平分线AD交BC于点D，且AB＝AD，作CM⊥AD交AD的延长线于M.求证：1()2AM AB AC=+.（三）角分线，分两边，对称全等要记全（截长）飞镖形辅助线都是在射线ON上取点B，使OB＝OA，从而使△OAC≌△OBC.1、如图，在△ABC中，∠BAC=60°，∠C=40°，AP平分∠BAC交BC于P，BQ平分∠ABC交AC于Q，求证：AB＋BP＝BQ＋AQ.2、在△ABC中，AB＞AC，AD是∠BAC的平分线，P是线段AD上任意一点（不与A重合）.求证：AB－AC＞PB－PC.3、如图，△ABC中，AB＝AC，∠A＝100°，∠B的平分线交AC于D，求证：AD＋BD＝BC.二、一线三等角模型（弦图模型）（不一定垂直，满足三个角相等即可）1、已知：如图所示，在△ABC中，AB＝AC，∠BAC＝90°，D为AC中点，AF⊥BD 于点E，交BC于F，连接DF.求证：∠ADB＝∠CDF.变式1、已知：如图所示，在△ABC中，AB＝AC，AM＝CN，AF⊥BM于E，交BC 于F，连接NF.求证：（1）∠AMB＝∠CNF；（2）BM＝AF＋FN.变式2、在变式1的基础上，其他条件不变，只是将BM和FN分别延长交于点P，求证：（1）PM＝PN；（2）PB＝PF＋AF.三、手拉手模型1、△ABE和△ACF均为等边三角形结论：（1）△ABF≌△AEC.（2）∠BOE＝∠BAE＝60°.（3）OA平分∠EOF.（四点共圆证）拓展：△ABC和△CDE均为等边三角形结论：（1）AD＝BE；（2）∠ACB＝∠AOB；（3）△PCQ为等边三角形；（4）PQ∥AE；（5）AP＝BQ；（6）CO平分∠AOE；（四点共圆证）（7）OA＝OB＋OC；（8）OE＝OC＋OD.（（7），（8）需构造等边三角形证明）1、△ABD和△ACE均为等腰直角三角形结论：（1）BE＝CD；（2）BE⊥CD.2、四边形ABEF和四边形ACHD均为正方形结论：（1）BD＝CF；（2）BD⊥CF.3、如图①，点M 为锐角三角形ABC 内任意一点，连接AM、BM、CM．以AB 为一边向外作等边三角形△ABE，将BM 绕点B 逆时针旋转60°得到BN，连接EN．（1）求证：△AMB≌△ENB；（2）若AM+BM+CM 的值最小，则称点M 为△ABC 的费尔马点．若点M 为△ABC 的费尔马点，试求此时∠AMB、∠BMC、∠CMA 的度数；（3）小翔受以上启发，得到一个作锐角三角形费尔马点的简便方法：如图②，分别以△ABC 的AB、AC 为一边向外作等边△ABE 和等边△ACF，连接CE、BF，设交点为M，则点M 即为△ABC 的费尔马点．试说明这种作法的依据．四、半角模型条件：1,+=1802αββθβ=︒且，两边相等.思路：1、补短（旋转）辅助线：①延长CD 到E，使ED=BM，连AE 或延长CB 到F，使FB=DN，连AF②将△ADN 绕点A 顺时针旋转90°得△ABF，注意：旋转需证F、B、M 三点共线结论：（1）MN＝BM＋DN；（2）=2CMN C AB ；（3）AM、AN 分别平分∠BMN、∠MND .2、翻折（对称）辅助线：①作AP⊥MN 交MN 于点P②将△ADN、△ABM 分别沿AN、AM 翻折，但一定要证明M、P、N 三点共线.例1、在正方形ABCD 中，若M、N 分别在边BC、CD 上移动，且满足MN＝BM＋DN，求证：（1）∠MAN＝45°；（2）=2CMN C AB ；（3）AM、AN 分别平分∠BMN 和∠DNM .变式：在正方形ABCD 中，已知∠MAN＝45°，若M、N 分别在边CB、DC 的延长线上移动，AH⊥MN，垂足为H，（1）试探究线段MN、BM、DN 之间的数量关系；（2）求证：AB＝AH例2、在四边形ABCD中，∠B＋∠D＝180°，AB＝AD，若E、F分别为边BC、CD上的点，且满足EF＝BE＋DF，求证：12EAF BAD ∠=∠.变式：在四边形ABCD中，∠B＝90°，∠D＝90°，AB＝AD，若E、F分别为边BC、CD上的点，且12EAF BAD∠=∠，求证：EF＝BE＋DF.。

（1）.例题应用：①如图1,在,中ABC ∆900=∠AD C 平分，.求证：︒=∠+∠180C A 图3练习二：已知如图4,四边形ABCD 中,图4练习三：如图5,交CD 于点E,交CB 于点F.(1)求证：CE=CF.(2)将图5中地△ADE 沿AB 向右平移到地位置,使点落在BC 边上,其他款件不变,如图6所示,是猜想：于CF 又怎样地数量关系？请证明你地结论.图5 图6练习四：如图7,90A AD BC =︒，∠∥,P 是AB 地中点,PD 平分∠ADC．..,1800BAD AC CD BC D B ∠==∠+∠平分求证：,,900CAB AF D AB CD ACB ABC Rt ∠⊥=∠∆平分，垂足为，中，'''E D A ∆'E 'BE△BAC地外角平分线AD于点D,F(3).模型巩固：练习一，如图3,ΔABC是等腰直角三角形延长线于点E。

求证：BD=2CE。

图3图4ABC 中,CE 平分∠ACB,且AE ⊥CE,∠AED ＋，90=∠D DCO EC ∠是图7（a ） 图7（b ） 图7（c ）②，如图7（b ）,分别是、CE BD 为ABC BD ∆图8练习六，如图9所示,在ABC ∆中,AC AB >,M 为BC 地中点,AD 是BAC ∠地平分线,若CF AD ⊥且交AD 地延长线于F ,求证()12MF AC AB =-．图9练习六变形一：如图10所示,AD 是ABC ∆中BAC ∠地外角平分线,CD AD ⊥于D ,E 是BC 地中点,求证DE AB ∥ 且1()2DE AB AC =+．图10练习六变形二：如图11所示,在ABC ∆中,AD 平分BAC ∠,AD AB =,CM AD ⊥于M ,求证2AB AC AM +=．图11练习七，如图12,在ABC ∆中,2B C ∠=∠,BAC ∠地平分线AD 交BC 与D ．则有AB BD AC +=．那么如图13,已知在ABC ∆中,3ABC C ∠=∠,12∠=∠,BE AE ⊥．求证：2AC AB BE -=．GABC D EF12MFD CB AE DCB AMD CBA两个图形地辅助线都是在射线OA 上取点B ,使OB=OA ,从而使≌△OBC.OAC ∆思路思路：1）题意思路：本题考查全等三角形常见辅助线地知识：作平行线。