北京四中 高中数学高考综合复习二项式定理

高中数学二项式定理知识点总结（精选4篇）高中数学二项式定理知识点总结（精选4篇）每个人都可以通过不断学习、积累知识来提高自己的竞争力和创造力。

拥有广博的知识储备可以为人生带来更多的选择和机会。

下面就让小编给大家带来高中数学二项式定理知识点总结，希望大家喜欢!高中数学二项式定理知识点总结篇1空间两条直线只有三种位置关系：平行、相交、异面1、按是否共面可分为两类：(1)共面：平行、相交(2)异面：异面直线的定义：不同在任何一个平面内的两条直线或既不平行也不相交。

异面直线判定定理：用平面内一点与平面外一点的直线，与平面内不经过该点的直线是异面直线。

两异面直线所成的角：范围为(0°，90°)esp.空间向量法两异面直线间距离:公垂线段(有且只有一条)esp.空间向量法2、若从有无公共点的角度看可分为两类：(1)有且仅有一个公共点——相交直线;(2)没有公共点——平行或异面直线和平面的位置关系：直线和平面只有三种位置关系：在平面内、与平面相交、与平面平行①直线在平面内——有无数个公共点②直线和平面相交——有且只有一个公共点直线与平面所成的角：平面的一条斜线和它在这个平面内的射影所成的锐角。

高中数学二项式定理知识点总结篇21、求函数的单调性：利用导数求函数单调性的基本方法：设函数yf(x)在区间(a，b)内可导，(1)如果恒f(x)0，则函数yf(x)在区间(a，b)上为增函数;(2)如果恒f(x)0，则函数yf(x)在区间(a，b)上为减函数;(3)如果恒f(x)0，则函数yf(x)在区间(a，b)上为常数函数。

利用导数求函数单调性的基本步骤：①求函数yf(x)的定义域;②求导数f(x);③解不等式f(x)0，解集在定义域内的不间断区间为增区间;④解不等式f(x)0，解集在定义域内的不间断区间为减区间。

反过来，也可以利用导数由函数的单调性解决相关问题(如确定参数的取值范围)：设函数yf(x)在区间(a，b)内可导，(1)如果函数yf(x)在区间(a，b)上为增函数，则f(x)0(其中使f(x)0的x值不构成区间);(2)如果函数yf(x)在区间(a，b)上为减函数，则f(x)0(其中使f(x)0的x值不构成区间);(3)如果函数yf(x)在区间(a，b)上为常数函数，则f(x)0恒成立。

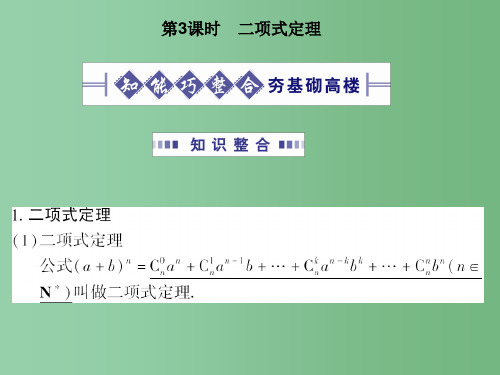
二项式定理知识点与题型复习一、基础知识1.二项式定理(1)二项式定理：(a＋b)n＝C0n a n＋C1n a n－1b＋…＋C k n a n－k b k＋…＋C n n b n(n∈N*)(2)通项公式：T k＋1＝C k n a n－k b k，它表示第k＋1项；(3)二项式系数：二项展开式中各项的系数为C0n，C1n，…，C n n.2.二项式系数的性质注：(1)项数为n＋1.(2)各项的次数都等于二项式的幂指数n，即a与b的指数的和为n.(3)字母a按降幂排列，从第一项开始，次数由n逐项减1直到零；字母b按升幂排列，从第一项起，次数由零逐项增1直到n.二项式系数与项的系数的区别二项式系数是指C0n，C1n，…，C n n，它只与各项的项数有关，而与a，b的值无关；而项的系数是指该项中除变量外的常数部分，它不仅与各项的项数有关，而且也与a，b的值有关.如(a＋bx)n的二项展开式中，第k＋1项的二项式系数是C k n，而该项的系数是C k n a n－k b k.当然，在某些二项展开式中，各项的系数与二项式系数是相等的.二、考点解析考点一二项展开式中特定项或系数问题考法(一)求解形如(a＋b)n(n∈N*)的展开式中与特定项相关的量例1、(1)522⎪⎭⎫⎝⎛+xx的展开式中x4的系数为()A.10B.20C.40D.80(2)若(2x－a)5的二项展开式中x3的系数为720，则a＝________.(3)已知5⎪⎭⎫⎝⎛+xax的展开式中x5的系数为A，x2的系数为B，若A＋B＝11，则a＝________.[解题技法]求形如(a＋b)n(n∈N*)的展开式中与特定项相关的量(常数项、参数值、特定项等)的步骤第一步，利用二项式定理写出二项展开式的通项公式T r＋1＝C r n a n－r b r，常把字母和系数分离开来(注意符号不要出错)；第二步，根据题目中的相关条件(如常数项要求指数为零，有理项要求指数为整数)先列出相应方程(组)或不等式(组)，解出r；第三步，把r代入通项公式中，即可求出T r＋1，有时还需要先求n，再求r，才能求出T r＋1或者其他量.考法(二)求解形如(a＋b)m(c＋d)n(m，n∈N*)的展开式中与特定项相关的量例2、(1)(1－x)6(1＋x)4的展开式中x的系数是()A.－4B.－3C.3D.4(2)已知(x－1)(ax＋1)6的展开式中含x2项的系数为0，则正实数a＝________.[解题技法]求形如(a＋b)m(c＋d)n(m，n∈N*)的展开式中与特定项相关的量的步骤第一步，根据二项式定理把(a＋b)m与(c＋d)n分别展开，并写出其通项公式；第二步，根据特定项的次数，分析特定项可由(a＋b)m与(c＋d)n的展开式中的哪些项相乘得到；第三步，把相乘后的项合并即可得到所求特定项或相关量.考法(三)求形如(a＋b＋c)n(n∈N*)的展开式中与特定项相关的量例3、(1)(x2＋x＋y)5的展开式中x5y2的系数为()A.10B.20C.30D.60(2)将344⎪⎭⎫⎝⎛-+xx展开后，常数项是________.[解题技法]求形如(a＋b＋c)n(n∈N*)的展开式中与特定项相关的量的步骤第一步，把三项的和a＋b＋c看成是(a＋b)与c两项的和；第二步，根据二项式定理写出[(a ＋b )＋c ]n 的展开式的通项；第三步，对特定项的次数进行分析，弄清特定项是由(a ＋b )n －r 的展开式中的哪些项和c r 相乘得到的； 第四步，把相乘后的项合并即可得到所求特定项或相关量. 跟踪训练1.在(1－x 3)(2＋x )6的展开式中，x 5的系数是________.(用数字作答)3.5212⎪⎭⎫⎝⎛++x x (x ＞0)的展开式中的常数项为________.考点二 二项式系数的性质及各项系数和[典例精析](1)若531⎪⎪⎭⎫ ⎝⎛+x x 的展开式中各项系数之和大于8，但小于32，则展开式中系数最大的项是( ) A.63x B.4x C.4x 6x D.4x或4x 6x(2)若nx x ⎪⎭⎫ ⎝⎛-12的展开式中含x 的项为第6项，设(1－3x )n ＝a 0＋a 1x ＋a 2x 2＋…＋a n x n ，则a 1＋a 2＋…＋a n的值为________.(3)若(a ＋x )(1＋x )4的展开式中x 的奇数次幂项的系数之和为32，则a ＝________.[解题技法] 1.赋值法的应用二项式定理给出的是一个恒等式，对于x ，y 的一切值都成立.因此，可将x ，y 设定为一些特殊的值.在使用赋值法时，令x ，y 等于多少，应视具体情况而定，一般取“1，－1或0”，有时也取其他值.如： (1)形如(ax ＋b )n ，(ax 2＋bx ＋c )m (a ，b ，c ∈R )的式子，求其展开式的各项系数之和，只需令x ＝1即可. (2)形如(ax ＋by )n (a ，b ∈R )的式子，求其展开式各项系数之和，只需令x ＝y ＝1即可. 2.二项展开式各项系数和、奇数项系数和与偶数项系数和的求法 若f (x )＝a 0＋a 1x ＋a 2x 2＋…＋a n x n ，则f (x )的展开式中 (1)各项系数之和为f (1).(2)奇数项系数之和为a 0＋a 2＋a 4＋…＝f (1)＋f (－1)2.(3)偶数项系数之和为a 1＋a 3＋a 5＋…＝f (1)－f (－1)2.跟踪训练1.已知(2x－1)5＝a5x5＋a4x4＋a3x3＋a2x2＋a1x＋a0，则|a0|＋|a1|＋…＋|a5|＝()A.1B.243C.121D.1222.若(x＋2＋m)9＝a0＋a1(x＋1)＋a2(x＋1)2＋…＋a9(x＋1)9，且(a0＋a2＋…＋a8)2－(a1＋a3＋…＋a9)2＝39，则实数m的值为________.3.已知(1＋3x)n的展开式中，后三项的二项式系数的和等于121，则展开式中二项式系数最大的项为____.考点三二项展开式的应用例、设a∈Z，且0≤a＜13，若512 018＋a能被13整除，则a＝()A.0B.1C.11D.12[解题技法]利用二项式定理解决整除问题的思路(1)要证明一个式子能被另一个式子整除，只要证明这个式子按二项式定理展开后的各项均能被另一个式子整除即可.因此，一般要将被除式化为含相关除式的二项式，然后再展开.(2)用二项式定理处理整除问题，通常把底数写成除数(或与除数密切关联的数)与某数的和或差的形式，再用二项式定理展开.但要注意两点：①余数的范围，a＝cr＋b，其中余数b∈[0，r)，r是除数，若利用二项式定理展开变形后，切记余数不能为负；②二项式定理的逆用.跟踪训练]1.使得多项式81x4＋108x3＋54x2＋12x＋1能被5整除的最小自然数x为()A.1B.2C.3D.4课后作业1.3422⎪⎪⎭⎫ ⎝⎛+x x 的展开式中的常数项为( ) A.－32 B.32 C.6 D.－6 2.设(2－x )5＝a 0＋a 1x ＋a 2x 2＋…＋a 5x 5，则a 2＋a 4a 1＋a 3的值为( )A.－6160B.－122121C.－34D.－901213.若二项式72⎪⎭⎫ ⎝⎛+x a x 的展开式的各项系数之和为－1，则含x 2项的系数为( )A.560B.－560C.280D.－2804.已知(1＋x )n 的展开式中第5项与第7项的二项式系数相等，则奇数项的二项式系数和为( ) A.29 B.210 C.211 D.2125.二项式9221⎪⎭⎫⎝⎛-x x 的展开式中，除常数项外，各项系数的和为( )A.－671B.671C.672D.673 6.在(1－x )5(2x ＋1)的展开式中，含x 4项的系数为( )A.－5B.－15C.－25D.257.若(x 2－a )101⎪⎭⎫ ⎝⎛+x x 的展开式中x 6的系数为30，则a 等于( )A.13B.12C.1D.2 8.若(1＋mx )6＝a 0＋a 1x ＋a 2x 2＋…＋a 6x 6，且a 1＋a 2＋…＋a 6＝63，则实数m 的值为( ) A.1或3 B.－3 C.1 D.1或－3 9.(2x －1)6的展开式中，二项式系数最大的项的系数是________.(用数字作答)10.9⎪⎭⎫ ⎝⎛+x a x 的展开式中x 3的系数为－84，则展开式的各项系数之和为________.11.511⎪⎭⎫ ⎝⎛++x x 展开式中的常数项为________.12.已知nx x ⎪⎪⎭⎫ ⎝⎛+41的展开式中，前三项的系数成等差数列. (1)求n ；(2)求展开式中的有理项；(3)求展开式中系数最大的项.。

第三节二项式定理1．能利用计数原理证明二项式定理．2．会用二项式定理解决与二项展开式有关的简单问题．1．二项式定理2．二项式系数的性质1．二项式(x＋y)n的展开式的第k＋1项与(y＋x)n的展开式的第k＋1项一样吗？提示：尽管(x＋y)n与(y＋x)n的值相等，但它们的展开式形式是不同的，因此应用二项式定理时，x，y的位置不能随便交换．2．二项式系数与项的系数一样吗？提示：不一样．二项式系数是指C0n，C1n，…，C n n，它只与各项的项数有关，而与a，b的值无关；而项的系数是指该项中除变量外的常数部分，它不仅与各项的项数有关，而且也与a，b的值有关．1．(x －y )n 的二项展开式中，第r 项的系数是( )A ．C r nB ．C r ＋1nC ．C r －1nD ．(－1)r －1C r －1n 解析：选D 本题中由于y 的系数为负，故其第r 项的系数为(－1)r －1C r －1n .2．(1＋x )7的展开式中x 2的系数是( ) A ．42 B ．35 C ．28 D ．21解析：选D 依题意可知，二项式(1＋x )7的展开式中x 2的系数等于C 27×15＝21.3．C 16＋C 26＋C 36＋C 46＋C 56＋C 66的值为( )A ．62B ．63C ．64D ．65解析：选B 因为C 16＋C 26＋C 36＋C 46＋C 56＋C 66＝(C 06＋C 16＋C 26＋C 36＋C 46＋C 56＋C 66)－C 06＝26－1＝63.4.⎝ ⎛⎭⎪⎫x ＋2x 2n 展开式中只有第6项的二项式系数最大，则n 等于________．解析：∵展开式中只有第6项的二项式系数最大， ∴n ＝10. 答案：105．(A.嘉兴模拟)(x ＋1)9的展开式中x 3的系数是________．(用数字作答) 解析：依题意知：(x ＋1)9的展开式中x 3的系数为C 69＝C 39＝9×8×73×2×1＝84.答案：841．二项式定理是高中数学中的一个重要知识点，也是高考命题的热点，多以选择、填空题的形式呈现，试题难度不大，多为容易题或中档题．2．高考对二项式定理的考查主要有以下几个命题角度： (1)求二项展开式中的第n 项； (2)求二项展开式中的特定项；(3)已知二项展开式的某项，求特定项的系数．[例1] (1)(A.浙江高考)在(1＋x )6(1＋y )4的展开式中，记x m y n 项的系数为f (m ，n )，则f (3,0)＋f (2,1)＋f (1,2)＋f (0,3)＝( )A ．45B ．60C ．120D ．210(2)(A.四川高考)在x (1＋x )6的展开式中，含x 3项的系数为( ) A ．30 B ．20 C ．15 D ．10(3)(A.湖南高考)⎝ ⎛⎭⎪⎫12x －2y 5的展开式中x 2y 3的系数是( )A ．－20B ．－5C ．5D ．20(4)使⎝⎛⎭⎪⎫3x ＋1x x n (n ∈N *)的展开式中含有常数项的最小的n 为( ) A ．4 B ．5 C ．6 D ．7[自主解答] (1)由题意知f (3,0)＝C 36C 04，f (2,1)＝C 26C 14，f (1，2)＝C 16C 24，f (0,3)＝C 06C 34，因此f (3,0)＋f (2,1)＋f (1，2)＋f (0,3)＝120，选C.(2)只需求(1＋x )6的展开式中含x 2项的系数即可，而含x 2项的系数为C 26＝15，故选C.(3)由二项展开式的通项可得，第四项T 4＝C 35⎝ ⎛⎭⎪⎫12x 2·(－2y )3＝－20x 2y 3，故x 2y 3的系数为－20，选A.(4)T r ＋1＝C r n(3x )n －r·x －32r ＝C r n ·3n －r ·xn －r －32r ＝C r n ·3n －r·xn －5r 2(r ＝0,1,2，…，n )，若T r ＋1是常数项，则有n －52r ＝0，即2n ＝5r (r ＝0,1，…，n )，当r ＝0,1时，n ＝0，52，不满足条件；当r ＝2时，n ＝5.[答案] (1)C (2)C (3)A (4)B互动探究若本例(2)中的条件“n ∈N *”改为“n ≥3”，其他条件不变，则展开式中的有理项最少有________项．解析：由本例(2)中的自主解答可知：T r ＋1＝C r n3n －rxn －5r2(r ＝0,1,2，…，n )．即当⎝⎛⎭⎪⎫n －5r 2为整数时，T r ＋1为有理项．显然当n ＝3时，r 的取值最少，有r ＝0，r ＝2， 即有理项为T 1、T 3两项． 答案：2求二项式展开式有关问题的常见类型及解题策略(1)求展开式中的第n 项．可依据二项式的通项公式直接求出第n 项； (2)求展开式中的特定项．可依据条件写出第r ＋1项，再由特定项的特点求出r 值即可．(3)已知展开式的某项，求特定项的系数．可由某项得出参数项，再由通项公式写出第r ＋1项，由特定项得出r 值，最后求出其参数．1．若二项式⎝ ⎛⎭⎪⎫x －2x n 的展开式中第5项是常数项，则正整数n 的值可能为( )A ．6B ．10C ．12D ．15解析：选C T r ＋1＝C r n(x )n －r ⎝ ⎛⎭⎪⎫－2x r ＝(－2)r C r n x n －3r 2，当r ＝4时，n －3r 2＝0，又n ∈N *，所以n ＝12.2．(A.金华模拟)⎝ ⎛⎭⎪⎫2x ＋x (1－x )4的展开式中x 的系数是________．解析：⎝ ⎛⎭⎪⎫2x ＋x (1－x )4的展开式x 的项为2x ·C 4410(－x )4＋x C 0414(－x )0＝2x ＋x ＝3x .所以x 的系数为3.答案：3[例2] (1)设m 为正整数，(x ＋y )2m 展开式的二项式系数的最大值为a ，(x ＋y )2m ＋1展开式的二项式系数的最大值为b ，若13a ＝7b ，则m ＝( )A ．5B ．6C ．7D ．8(2)若C 3n ＋123＝C n ＋623(n ∈N *)且(3－x )n ＝a 0＋a 1x ＋a 2x 2＋…＋a n x n，则a 0－a 1＋a 2－…＋(－1)n a n ＝________.[自主解答] (1)由题意得：a ＝C m 2m ，b ＝C m 2m ＋1， 所以13C m 2m ＝7C m 2m ＋1，∴132mm ！·m ！＝72m ＋1mm ＋1，∴72m ＋1m ＋1＝13，解得m ＝6，经检验为原方程的解，选B.(2)由C 3n ＋123＝C n ＋623，得3n ＋1＝n ＋6(无整数解)或3n ＋1＝23－(n ＋6)，解得n ＝4，问题即转化为求(3－x )4的展开式中各项系数和的问题，只需在(3－x )4中令x ＝－1即得a 0－a 1＋a 2－…＋(－1)n a n ＝[3－(－1)]4＝256.[答案] (1)B (2)256方法规律 赋值法的应用(1)形如(ax ＋b )n ，(ax 2＋bx ＋c )m (a ，b ，c ∈R )的式子求其展开式的各项系数之和，常用赋值法，只需令x ＝1即可．(2)对形如(ax ＋by )n (a ，b ∈R )的式子求其展开式各项系数之和，只需令x ＝y ＝1即可．(3)若f (x )＝a 0＋a 1x ＋a 2x 2＋…＋a n x n ，则f (x )展开式中各项系数之和为f (1)，奇数项系数之和为a 0＋a 2＋a 4＋…＝f 1f 12，偶数项系数之和为a 1＋a 3＋a 5＋…＝f 1f 12.1．设(1＋x )n ＝a 0＋a 1x ＋…＋a n x n ，若a 1＋a 2＋…＋a n ＝63，则展开式中系数最大的项是( )A ．15x 3B ．20x 3C ．21x 3D ．35x 3解析：选B 在(1＋x )n ＝a 0＋a 1x ＋…＋a n x n 中，令x ＝1得2n ＝a 0＋a 1＋a 2＋…＋a n .令x ＝0，得1＝a 0，∴a 1＋a 2＋…＋a n ＝2n －1＝63，∴n ＝6.而(1＋x )6的展开式中系数最大的项为T 4＝C 36x 3＝20x 3.2．(A.丽水模拟)若(1－2x )2 014＝a 0＋a 1x ＋…＋a 2 013x 2 013＋a 2 014x 2 014(x ∈R )，则a 12＋a 222＋…＋a 2 01322 013＋a 2 01422 014的值为( ) A ．2 B ．0 C ．－1 D ．－2解析：选C 令x ＝0，则a 0＝1，令x ＝12，则a 0＋a 12＋a 222＋…＋a 2 01322 013＋a 2 01422 014＝0，∴a 12＋a 222＋…＋a 2 01322 013＋a 2 01422 014＝－1.—————————————[课堂归纳——通法领悟]——————————————1个公式——二项展开式的通项公式通项公式主要用于求二项式的特定项问题，在运用时，应明确以下几点：(1)C r n an －r b r是第r ＋1项，而不是第r 项； (2)通项公式中a ，b 的位置不能颠倒；(3)通项公式中含有a ，b ，n ，r ，T r ＋1五个元素，只要知道其中的四个，就可以求出第五个，即“知四求一”．3个注意点——二项式系数的三个注意点 (1)求二项式所有系数的和，可采用“赋值法”；(2)关于组合式的证明，常采用“构造法”——构造函数或构造同一问题的两种算法；(3)展开式中第r ＋1项的二项式系数与第r ＋1项的系数一般是不相同的，在具体求各项的系数时，一般先处理符号，对根式和指数的运算要细心，以防出错．前沿热点(十六)与二项式定理有关的交汇问题1．二项式定理作为一个独特的内容，在高考中总有所体现，常常考查二项式定理的通项、项的系数、各项系数的和等．2．二项式定理作为一个工具，也常常与其他知识交汇命题，如与数列交汇、与不等式交汇、与函数交汇等．因此在一些题目中不仅仅考查二项式定理，还要考查其他知识，其解题的关键点是它们的交汇点，注意它们的联系即可．[典例](B.陕西高考)设函数f (x )＝⎩⎨⎧⎝ ⎛⎭⎪⎫x －1x 6，x <0，－x ，x ≥0，则当x >0时，f [f (x )]表达式的展开式中常数项为( )A ．－20B ．20C ．－15D ．15[解题指导] 先寻找x >0时f (x )的取值，再寻找f [f (x )]的表达式，再利用二项式定理求解．[解析] x >0时，f (x )＝－x <0，故f [f (x )]＝⎝⎛⎭⎪⎫－x ＋1x 6，其展开式的通项公式为T r ＋1＝C r6·(－x )6－r·⎝ ⎛⎭⎪⎫1x r＝(－1)6－r ·C r 6·(x )6－2r ，由6－2r ＝0，得r ＝3，故常数项为(－1)3·C 36＝－20.[答案] A[名师点评] 解决本题的关键有以下几点： (1)正确识别分段函数f (x )； (2)正确判断f (x )的符号； (3)正确写出f [f (x )]的解析式； (4)正确应用二项式定理求出常数项.(A.安徽高考)设a ≠0，n 是大于1的自然数，⎝ ⎛⎭⎪⎫1＋x a n 的展开式为a 0＋a 1x ＋a 2x 2＋…＋a n x n .若点A i (i ，a i )(i ＝0,1,2)的位置如图所示，则a ＝________.解析：由题图可知a 0＝1，a 1＝3，a 2＝4，由题意知⎩⎪⎨⎪⎧C 1n ·1a＝a 1＝3，C 2n ·1a 2＝a 2＝4，故⎩⎪⎨⎪⎧na ＝3，n n －1a2＝8，可得⎩⎨⎧n ＝9，a ＝3.答案：31．在⎝ ⎛⎭⎪⎫2x 2－1x 5的二项展开式中，x 的系数为( )A ．10B ．－10C ．40D ．－40 解析：选D T r ＋1＝C r 5(2x 2)5－r ⎝ ⎛⎭⎪⎫－1x r ＝(－1)r ·25－r ·C r 5·x10－3r， 令10－3r ＝1，得r ＝3.所以x 的系数为(－1)3·25－3·C 35＝－40.2．在(1＋x )2－(1＋3x )4的展开式中，x 的系数等于( ) A ．3 B ．－3 C ．4 D ．－4解析：选B 因为(1＋x )2的展开式中x 的系数为1，(1＋3x )4的展开式中x 的系数为C 34＝4，所以在(1＋x )2－(1＋3x )4的展开式中，x 的系数等于－3.3．(A.金华模拟)(1＋x )8(1＋y )4的展开式中x 2y 2的系数是( ) A ．56 B ．84 C ．112 D ．168解析：选D (1＋x )8展开式中x 2的系数是C 28，(1＋y )4的展开式中y 2的系数是C 24，根据多项式乘法法则可得(1＋x )8(1＋y )4展开式中x 2y 2的系数为C 28C 24＝28×6＝168.4.⎝ ⎛⎭⎪⎫x ＋a x ⎝ ⎛⎭⎪⎫2x －1x 5的展开式中各项系数的和为2，则该展开式中常数项为( )A ．－40B ．－20C ．20D ．40解析：选D 由题意，令x ＝1得展开式各项系数的和为(1＋a )·(2－1)5＝2，∴a ＝1.∵二项式⎝⎛⎭⎪⎫2x －1x 5的通项公式为T r ＋1＝C r 5(－1)r ·25－r·x 5－2r ，∴⎝⎛⎭⎪⎫x ＋1x ⎝ ⎛⎭⎪⎫2x －1x 5展开式中的常数项为x ·C 35(－1)322·x －1＋1x·C 25·(－1)2·23·x ＝－40＋80＝40.5．在(1－x )n ＝a 0＋a 1x ＋a 2x 2＋a 3x 3＋…＋a n x n 中，若2a 2＋a n －3＝0，则自然数n 的值是( )A ．7B ．8C ．9D ．10解析：选B 易知a 2＝C 2n ，a n －3＝(－1)n －3·C n －3n ＝(－1)n －3C 3n ，又2a 2＋a n －3＝0，所以2C 2n ＋(－1)n －3C 3n ＝0，将各选项逐一代入检验可知n ＝8满足上式． 6．设a ∈Z ，且0≤a ＜13，若512 012＋a 能被13整除，则a ＝( ) A ．0 B ．1 C ．11 D ．12解析：选D 512 012＋a ＝(13×4－1)2 012＋a ，被13除余1＋a ，结合选项可得a ＝12时，512 012＋a 能被13整除．7．(A.新课标全国卷Ⅱ)(x ＋a )10的展开式中，x 7的系数为15，则a ＝________.(用数字填写答案)解析：二项展开式的通项公式为T r ＋1＝C r 10x10－r a r，当10－r ＝7时，r ＝3，T 4＝C 310a 3x 7，则C 310a 3＝15，故a ＝12. 答案：128．(A.山东高考)若⎝ ⎛⎭⎪⎫ax 2＋b x 6的展开式中x 3项的系数为20，则a 2＋b 2的最小值为________．解析：T r ＋1＝C r 6(ax 2)6－r ⎝ ⎛⎭⎪⎫b x r ＝C r 6a 6－r b r x 12－3r ，令12－3r ＝3，得r ＝3，故C 36a 3b 3＝20，所以ab ＝1，a 2＋b 2≥2ab ＝2，当且仅当a ＝b ＝1或a ＝b ＝－1时，等号成立．答案：29．(B.浙江高考)设二项式⎝⎛⎭⎪⎪⎫x －13x 5的展开式中常数项为A ，则A ＝________.解析：因为⎝ ⎛⎭⎪⎪⎫x －13x 5的通项T r ＋1＝C r 5(x )5－r ·⎝⎛⎭⎪⎪⎫－13x r ＝(－1)r C r 5x 5－r 2x －r 3＝(－1)r C r 5x15－5r 6. 令15－5r ＝0，得r ＝3，所以常数项为(－1)3C 35x 0＝－10.即A ＝－10. 答案：－1010．已知(1－2x )7＝a 0＋a 1x ＋a 2x 2＋…＋a 7x 7，求： (1)a 1＋a 2＋…＋a 7； (2)a 1＋a 3＋a 5＋a 7； (3)a 0＋a 2＋a 4＋a 6；(4)|a 0|＋|a 1|＋|a 2|＋…＋|a 7|. 解：令x ＝1，则a 0＋a 1＋a 2＋a 3＋a 4＋a 5＋a 6＋a 7＝－1.① 令x ＝－1，则a 0－a 1＋a 2－a 3＋a 4－a 5＋a 6－a 7＝37.② (1)∵a 0＝C 07＝1，∴a 1＋a 2＋a 3＋…＋a 7＝－2. (2)(①－②)÷2，得a 1＋a 3＋a 5＋a 7＝－1－372＝－1 094.(3)(①＋②)÷2，得a 0＋a 2＋a 4＋a 6＝－1＋372＝1 093.(4)∵(1－2x )7展开式中a 0、a 2、a 4、a 6大于零，而a 1、a 3、a 5、a 7小于零， ∴|a 0|＋|a 1|＋|a 2|＋…＋|a 7|＝(a 0＋a 2＋a 4＋a 6)－(a 1＋a 3＋a 5＋a 7) ＝1 093－(－1 094)＝2 187. 11．若某一等差数列的首项为C11－2n 5n－A2n －211－3n，公差为⎝ ⎛⎭⎪⎫52x －253x 2m的展开式中的常数项，其中m 是7777－15除以19的余数，则此数列前多少项的和最大？并求出这个最大值．解：设该等差数列为{a n }，公差为d ，前n 项和为S n . 由已知得⎩⎨⎧11－2n ≤5n ，2n －2≤11－3n ，又n ∈N *， ∴n ＝2，∴C 11－2n 5n －A 2n －211－3n ＝C 710－A 25＝C 310－A 25＝10×9×83×2－5×4＝100， ∴a 1＝100.∵7777－15＝(76＋1)77－15＝7677＋C 177·7676＋…＋C 7677·76＋1－15 ＝76(7676＋C 177·7675＋…＋C 7677)－14＝76M －14(M ∈N *)，∴7777－15除以19的余数是5，即m ＝5.∴⎝ ⎛⎭⎪⎫52x －253x 2m 的展开式的通项是T r ＋1＝C r 5·⎝ ⎛⎭⎪⎫52x 5－r ⎝ ⎛⎭⎪⎫－253x 2r ＝(－1)r C r 5⎝ ⎛⎭⎪⎫525－2rx 53r －5(r ＝0,1,2,3,4,5)，令53r －5＝0，得r ＝3，代入上式，得T 4＝－4，即d ＝－4，从而等差数列的通项公式是a n ＝100＋(n －1)×(－4)＝104－4n .设其前k 项之和最大，则⎩⎨⎧104－4k ≥0，104－4k ＋10，解得k ＝25或k ＝26，故此数列的前25项之和与前26项之和相等且最大，S 25＝S 26＝a 1＋a 252×25＝100＋104－4×252×25＝1 300.12．从函数角度看，组合数C r n 可看成是以r 为自变量的函数f (r )，其定义域是{r |r ∈N ，r ≤n }．(1)证明：f (r )＝n －r ＋1rf (r －1)； (2)利用(1)的结论，证明：当n 为偶数时，(a ＋b )n 的展开式中最中间一项的二项式系数最大．解：(1)证明：∵f (r )＝C r n＝n ！rn －r，f (r －1)＝C r －1n ＝n ！r －1n －r ＋1，∴n －r ＋1r f (r －1)＝n －r ＋1r ·n ！r －1n －r ＋1＝n ！rn －r.则f (r )＝n －r ＋1rf (r －1)成立． (2)设n ＝2k ， ∵f (r )＝n －r ＋1rf (r －1)，f (r －1)>0， ∴f r f r －1＝2k －r ＋1r . 令f (r )≥f (r －1)，则2k －r ＋1r≥1，则r ≤k ＋12(等号不成立)．∴当r ＝1,2，…，k 时，f (r )>f (r －1)成立．反之，当r ＝k ＋1，k ＋2，…，2k 时，f (r )<f (r －1)成立． ∴f (k )＝C k 2k 最大，即(a ＋b )n 的展开式中最中间一项的二项式系数最大． [冲击名校]1．已知(1＋ax )(1＋x )5的展开式中x 2的系数为5，则a ＝( ) A ．－4 B ．－3 C ．－2 D ．－1解析：选D 已知(1＋ax )(1＋x )5的展开式中，x 2的系数为C 25＋a C 15＝5，则a ＝－1.2．(A.湖州模拟)⎝ ⎛⎭⎪⎫2x ＋a x 6的展开式中1x 2的系数为－12，则实数a 的值为________．解析：二项式⎝ ⎛⎭⎪⎫2x ＋a x 6展开式中第r ＋1项为T r ＋1＝C r 6·(2x )6－r⎝ ⎛⎭⎪⎫a x r＝C r 6·26－r ·a r ·x 3－r ，当3－r ＝－2，即r ＝5时，含有1x2的项的系数是C 56·2·a5＝－12，解得a ＝－1.答案：－1。

专题03 二项式定理【母题来源】【2020年高考北京卷】在5(2)x -的展开式中，2x 的系数为（ ）． A. 5- B. 5C. 10-D. 10【答案】C【解析】()52x -展开式的通项公式为：()()()55215522r rrrrr r T Cx C x--+=-=-，令522r -=可得：1r =，则2x 的系数为：()()11522510C -=-⨯=-. 【名师点睛】二项式定理的核心是通项公式，求解此类问题可以分两步完成：第一步根据所给出的条件(特定项)和通项公式，建立方程来确定指数(求解时要注意二项式系数中n 和r 的隐含条件，即n ，r 均为非负整数，且n ≥r ，如常数项指数为零、有理项指数为整数等)；第二步是根据所求的指数，再求所求解的项．【命题意图】高考对本部分内容的考查以能力为主，重点考查二项式定理的通项公式及其应用，要求同学们熟练掌握并灵活应用二项式定理的通项公式，考查分类讨论的数学思想．【命题规律】高考试题对该部分内容考查的主要角度有两种：一种是利用通项公式求解指定的项；一种利用通项公式考查系数、指数问题，如常数项、2x 项的系数等．重点对该部分内容的考查仍将以能力考查为主，利用题意写出通项公式是关键，通项公式是解决本类问题的核心与灵魂． 【答题模板】解答本类题目，一般考虑如下两步： 第一步：考查()na b +的展开式的通项公式其通项公式为1C r n r rr n T a b -+=，通项公式是后面进行讨论和计算的基础；第二步：结合代数式的整体进行考查结合题意，考查r 的某个值的特殊情形，据此分类讨论即可求得的系数． 【方法总结】 1．二项式()()na b n *+∈N 展开式()011222nn n n r n r rn nn n n n n a b C a C a b C a b C a b C b ---+=++++++，从恒等式中我们可以发现以下几个特点： （1）()na b +完全展开后的项数为()1n +；（2）展开式按照a 的指数进行降幂排列，对于展开式中的每一项，,a b 的指数呈此消彼长的特点．指数和为n ；（3）在二项式展开式中由于按a 的指数进行降幂排列，所以规定“+”左边的项视为a ，右边的项为b ，比如：()1n x +与()1nx +虽然恒等，但是展开式却不同，前者按x 的指数降幂排列，后者按1的指数降幂排列．如果是()na b -，则视为()na b +-⎡⎤⎣⎦进行展开；（4）二项展开式的通项公式1r n r rr n T C a b -+= （注意是第1r +项）．2．二项式系数：项前面的01,,,n n n n C C C 称为二项式系数，二项式系数的和为2n；二项式系数的来源：多项式乘法的理论基础是乘法的运算律（分配律，交换律，结合律），所以在展开时有这样一个特征：每个因式都必须出项，并且只能出一项，将每个因式所出的项乘在一起便成为了展开时中的某项．对于()na b +可看作是n 个()a b +相乘，对于n rr ab - 意味着在这n 个()a b +中，有()n r -个式子出a ，剩下r 个式子出b ，那么这种出法一共有r n C 种．所以二项式展开式的每一项都可看做是一个组合问题．而二项式系数便是这个组合问题的结果． 3．系数：是指该项经过化简后项前面的数字因数．注：（1）在二项式定理中要注意区分二项式系数与系数．二项式系数是展开式通项公式中的C rn ，对于确定的一个二项式，二项式系数只由r 决定．而系数是指展开并化简后最后项前面的因数，其构成一方面是二项式系数，同时还有项本身的系数．例如：()521x +展开式中第三项为()32235C 21T x =⋅⋅，其中25C 为该项的二项式系数，而()322335C 2180T x x =⋅⋅=，化简后的结果80为该项的系数．（2）二项式系数与系数的概念不同，但在某些情况下可以相等：当二项式中每项的系数均为1时（排除项本身系数的干扰），则展开后二项式系数与系数相同．例如()51x + 展开式的第三项为()32235C 1T x =⋅⋅，可以计算出二项式系数与系数均为10．4．有理项：系数为有理数，次数为整数的项，比如212,5x x就是有理项，而3,5x x 就不是有理项． 5．()na b +与()na b -的联系 首先观察他们的通项公式，()na b +：1r n r r r n T C a b -+=；()n a b -：()()'11r rr n r r n r rr n n T C a b C a b --+=-=-．两者对应项的构成是相同的，对应项的系数相等或互为相反数．其绝对值相等．所以在考虑()na b -系数的绝对值问题时，可将其转化为求()na b +系数的问题．1．（2020·北京八中高三月考）在621x x -⎛⎫ ⎪⎝⎭的展开式中，常数项是（ ） A ．20-B ．15-C ．15D ．302．（2020·北京十二中高二月考（理））522a x x ⎛⎫- ⎪⎝⎭的展开式中，含7x 项的系数为40，则a =（ ）A ．12B ．12-C ．2D ．－23．（2020·北京牛栏山一中高三月考）在()52x -的展开式中，2x 的系数是（ ）A ．80-B ．10-C ．5D ．404．（2020·北京高三一模）5212x x ⎛⎫+ ⎪⎝⎭的展开式中，4x 的系数是( ) A ．160B ．80C ．50D ．105．（2020·辽宁省高二期中）已知(1)nx +的展开式中第4项与第8项的二项式系数相等，则奇数项的二项式系数和为（ ）． A ．122B ．112C ．102D ．926．（2020·北京高三一模）在61(2)x x-的展开式中，常数项为（ ）A ．120-B ．120C ．160-D ．1607．（2020·北京高考真题）在52)-的展开式中，2x 的系数为（ ）． A ．5-B ．5C ．10-D ．108．（2020·北京高三一模）在612x x ⎛⎫- ⎪⎝⎭的展开式中，常数项是（ ）A ．160-B ．20-C ．20D ．1609．（2020·山东省菏泽一中高三月考）在二项式521x x ⎛⎫- ⎪⎝⎭的展开式中，含4x 的项的系数是（ ）．A ．10-B ．5-C ．10D ．510．（2020·北京理工大学附属中学通州校区高二期中）已知(a －x )5＝a 0＋a 1x ＋a 2x 2＋…＋a 5x 5，若a 2＝80，则a 0＋a 1＋a 2＋…＋a 5＝ ( ) A ．32B ．1C ．－243D ．1或－24311．（2020·北京高三一模）在二项式（1﹣2x ）5的展开式中，x 3的系数为（ ） A ．40B ．﹣40C ．80D ．﹣8012．（2020·北京高三期末）在51x x ⎛⎫- ⎪⎝⎭的展开式中，3x 的系数为（ ） A ．5-B ．5C ．10-D ．1013．（2020·广东省高三其他（理））已知二项式2(*)nx n N⎛-∈ ⎝的展开式中第2项与第3项的二项式系数之比是2︰5，则3x 的系数为（ ） A ．14B ．14-C ．240D ．240-14．（2020·北京高三期末（理））在62⎛⎫⎝的二项展开式中，2x 的系数为（ ） A ．154-B ．154C ．38-D ．3815．（2018·北方工业大学附属学校高三开学考试（理））已知21nx x ⎛⎫ ⎪⎝⎭+的二项展开式的各项系数和为32，则二项展开式中x 的系数为（ ） A ．5B ．10C ．20D ．4016．（2020·北京高三一模）在(2)nx -的展开式中，只有第三项的二项式系数最大，则含x 项的系数等于（ ）A ．32-B ．24-C ．8D ．417．（2020·吉林省长春十一高高三月考（理））若6(n x+的展开式中含有常数项，则n 的最小值等于A ．3B ．4C ．5D ．618．（2020·北京101中学高三月考（理））()51(1)1x x++的展开式中2x 的系数为 A ．10B ．15C ．20D ．2519．（2020·北京市建华实验学校高三月考）设()()612f x x =-，则x 的奇次项的系数和为______．20．（2020·北京高三一模）设常数a R ∈，如果52a x x ⎛⎫+ ⎪⎝⎭的二项展开式中x 项的系数为-80，那么a =______.21．（2020·宜宾市叙州区第一中学校高三二模（理））在二项式251x )x-（的展开式中，含4x 的项的系数是________．22．（2020·山西省高三其他（理））二项式62()x x-的展开式中，常数项为__________． 23．（2020·上海高三专题练习）设常数a R ∈，若25()a x x+的二项展开式中7x 项的系数为-10，则a =________．24．（2020·黑龙江省大庆四中高二月考（理））6x x ⎛⎪⎭-的展开式中的常数项为______．（用数字作答） 25．（2020·辽河油田第二高级中学高三其他（理））在()52x -的展开式中，3x 项的系数是__________（用数字作答）．26．（2020·北京市鲁迅中学高二月考）二项式261(2)x x-的展开式中的常数项是_______.（用数字作答）27．（2020·天津市武清区杨村第一中学高三开学考试）若2019(12)x -=a 0+ a 1x+…+a 2019x 2019（x∈R），则12a +222a +…+201920192a 的值为_______． 28．（2020·江西省高三其他（理））在61()x x-的展开式中的常数项为_______.29．（2020·首都师范大学附属中学高三其他）若52ax x ⎛+ ⎪⎝⎭的展开式中常数是80-，则实数a =______30．（2018·北京高三二模（理））的二项展开式中，的系数是________________（用数字作答）．31．（2020·北京十五中高三一模）已知7()ax x-展开式中5x 的系数为21，则实数a 的值为_____.32．（2020·北京市育英学校高三月考）12x ⎛⎝展开式中的常数项为__________.33．（2020·山西省山西大附中高三月考（理））在2nx ⎫⎪⎭的二项式中，所有项的二项式系数之和为256，则常数项等于______．34．（2020·北京高三一模）52()x x-的展开式中含3x 的系数为__________．（用数字填写答案） 35．（2020·北京人大附中高三月考）代数式（1﹣x ）（1+x ）5的展开式中x 3的系数为_____．36．（2020·北京高三月考）在52x ⎫⎪⎭的二项展开式中，2x -的系数为________（用数字作答） 37．（2020·北京人大附中昌平学校高三二模）在二项式()622x +的展开式中，8x 的系数为________.38．（2020·全国高三月考（理））在261()x x+的展开式中，含3x 项的系数为_________.（用数字填写答案）39．（2020·北京高三一模）在52x x ⎛⎫- ⎪⎝⎭的二项展开式中，3x -的系数为________.（用数字作答） 40．（2020·北京八十中高三开学考试）若()2345501234512a a x a x a x a x a x x =+++-++，则3a =__________(用数字作答)．解析附后专题03 二项式定理【答案】C【解析】()52x -展开式的通项公式为：()()()55215522r rrrrr r T C x C x--+=-=-，令522r -=可得：1r =，则2x 的系数为：()()11522510C -=-⨯=-. 【名师点睛】二项式定理的核心是通项公式，求解此类问题可以分两步完成：第一步根据所给出的条件(特定项)和通项公式，建立方程来确定指数(求解时要注意二项式系数中n 和r 的隐含条件，即n ，r 均为非负整数，且n ≥r ，如常数项指数为零、有理项指数为整数等)；第二步是根据所求的指数，再求所求解的项．1．【答案】C【解析】621x x -⎛⎫ ⎪⎝⎭的展开式的通项公式为()()623616611rrrr r r r T C x C x x --+⎛⎫=-=- ⎪⎝⎭，令360r -=，则2r ，故常数项为()2236115T C =-=，故选：C. 2．【答案】A【解析】522a x x ⎛⎫- ⎪⎝⎭展开式的通项公式为()()5351552522rr r rrr r r a T C x C x x a ---+=⎛⎫=- ⎪⎝⎭-，令357r -=，则4r =，故7x 的系数为()4545428040C a a --==，故12a =. 3．【答案】A【解析】因为()52x -的展开式的通项为()()5515522k kk k kk k T C x C x --+=-=-，令3k =，则2x 的系数是()335280C ⨯-=-.4．【答案】B【解析】依题5212x x ⎛⎫+ ⎪⎝⎭的展开式的通项为:2551031551(2)()2r r r r r r r T C x C x x---+==，当1034r -=时，2r，此时523552280r rC C -==，所以5212x x ⎛⎫+ ⎪⎝⎭的展开式中，4x 的系数是80. 5．【答案】D【解析】因为(1)nx +的展开式中第4项与第8项的二项式系数相等，所以，解得，所以二项式10(1)x +中奇数项的二项式系数和为．6．【答案】C【解析】61(2)x x-展开式的通项2616(1)2k k k k kT C x ，令260,3k k常数项333316(1)2=160T C7．【答案】C 【解析】)52x 展开式的通项公式为：(()()55215522rrrrrr r T C x C x--+=-=-，令522r -=可得：1r =，则2x 的系数为：()()11522510C -=-⨯=-. 8．【答案】A【解析】612x x ⎛⎫- ⎪⎝⎭展开式的通项公式为()()()66621662112r r r r r r rr r T C x x C x ----+=⋅⋅-⋅=-⋅⋅⋅，令620r -=，可得3r =，故612x x ⎛⎫- ⎪⎝⎭展开式的常数项为368160C -⋅=-，故选：A.9．【答案】C【解析】对于251031551()()(1)r rr r r r r T C x C x x--+=-=-， 对于10﹣3r ＝4， ∴r ＝2，则x 4的项的系数是C 52（﹣1）2＝10 故选C ． 10．【答案】B【解析】由题意233251080a C a a ===，∴2a =．在55015(2)x a a x a x -=+++中令1x =得5015(21)1a a a +++=-=．11．【答案】D【解析】因为（1﹣2x ）5展开式的通项公式为5rC •（﹣2x ）r ， 令r ＝3，所以x 3系数为35C •（﹣2）3＝﹣80，故选：D. 12．【答案】A【解析】51x x ⎛⎫- ⎪⎝⎭的展开式通项为()5525511kk k k k k C x C x x --⎛⎫⋅⋅-=⋅-⋅ ⎪⎝⎭，令523k -=，得1k =.因此，3x 的系数为()1515C ⋅-=-.13．【答案】C【解析】二项展开式的第1r +项的通项公式为()12rn rrr nT Cx -+⎛= ⎝由展开式中第2项与第3项的二项式系数之比是2︰5，可得：12:2:5n n C C =. 解得：6n =.所以()()366216221rr n rr rr r r n T C x C x---+⎛==- ⎝ 令3632r -=，解得：2r ，所以3x 的系数为()2262621240C --=14．【答案】C【解析】因为1r T +=66((2rr r C -⋅⋅,可得1r =时，2x 的系数为38-，C 正确.15．【答案】B【解析】因为二项展开式的各项系数和012232n n n n n n C C C C +++==，所以5n =，又二项展开式的通项为211()()r rn rr n T C x x-+==3r r n n C x -，351r -=，2r所以二项展开式中x 的系数为2510C =．答案选择B ．16．【答案】A【解析】由题意得4n =，∴414(2),0,,4r r r r T C x r -+=-=，当3r =时，3344(2)32T C x x =⋅⋅-=-，∴含x 项的系数等于32-，故选：A.17．【答案】C【解析】由题意6nx⎛ ⎝的展开式的3156666221r r r n r r r n r r n r n n n T C x C xC x ----+===（ ， 令15602n r -= ，得54n r =，当4r = 时，n 取到最小值5 18．【答案】C【解析】()5111x x ⎛⎫++ ⎪⎝⎭=11x ⎛⎫+ ⎪⎝⎭122334455555551+).C x C x C x C x C x ++++（ 所以()5111x x ⎛⎫++ ⎪⎝⎭的展开式中2x 的系数=2355101020.C C +=+=故选C.19．【答案】364-【解析】设()()623456012345612f x x a a x a x a x a x a x a x =-=++++++， 当1x =时，01234561a a a a a a a =++++++，（1）当1x =-时，601234563a a a a a a a =-+-+-+，（2）（1）-（2）得613513513,3642a a a a a a -=++∴++=-.所以x 的奇次项的系数和为364-. 20．【答案】2-【解析】52a x x ⎛⎫+ ⎪⎝⎭的二项展开式的通项公式：()52103155rr r r r r r a T C x a C x x --+⎛⎫== ⎪⎝⎭， 令1031r -=，解得3r =.∴33580a C =-，解得2a =-. 21．【答案】10 【解析】251031551()()(1)r r r r r r r T C x C x x--+=-=- ，所以令1034r -=得2r ，即含4x 的项的系数是225(1)=10.C -22．【答案】160- 【解析】6621662)2),0,1,,6((r r r r rr r T C x C x r x--+-==-=，当6203r r -=⇒=时，∴463302(6)1T C =-=-，∴常数项为160-，23．【答案】-2【解析】∵25()a x x +的展开式的通项为102103155()r r rr r r r a T C xC a x x--+==，令1037r -=，得1r =， ∴7x 的系数是155aC a =，∵7x 项的系数为-10，∴510a =-，得2a =-.24．【答案】-20【解析】6的展开式的通项为：()631661rrr r r r r T C C x --+⎛==- ⎝. 取3r =得到常数项为：3620C -=-.25．【答案】40-【解析】()52x -的展开式的通项为：552()rrr C x --.令3r =，得5352()40rrr C x x --=-.【解析】有题意可得，二项式展开式的通项为：()62612316612(1)2rrr r r r rr T C xC xx ---+⎛⎫=-=- ⎪⎝⎭令1230r -=可得4r = ，此时2456260T C ==.27．【答案】1-【解析】令等式中得；再令,则,所以,故应填.28．【答案】20-【解析】61()x x-的通项公式为：T r +1661()r r r x x-=-=（-1）r6r x 6﹣2r ．令6﹣2r ＝0 解得r ＝3， ∴（-1）336=-20，所以常数项为-20．29．【答案】16-【解析】根据二项定理展开式的通项可知()2551052155rrr r r rr ax x T CC a x ---+⎛⎫==，所以51002r-=，即4r =时为常数项， 所以454580C a-=-，解得16a =-，【解析】，，所以系数为10．31．【答案】-3【解析】因为7a x x ⎛⎫- ⎪⎝⎭的展开式中的通项()772177rr r r r rr a T C x a C xx --+⎛⎫=-=- ⎪⎝⎭ 令7-2r=5，可得r=11721,3a C a -⋅=∴=-32．【答案】220-【解析】123x x ⎛ ⎝展开式中第1k +项为 412123112123((1),0,1,2,12k k k k k kk T C xC x k x--+==-=，令4120,93k k -==，所以常数项为931212220C C -=-=-. 33．【答案】112【解析】由题意可得：2256,8nn =∴=，结合二项式展开式通项公式可得：()8483318822rrrr r r r T C x C x x --+⎛⎫=-=- ⎪⎝⎭，令8403r-=可得：2r ，则常数项为：()2282428112C -=⨯=.34．【答案】10【解析】由题意得，二项式展开式的通项为5521552()(2)r rr r r r r T C xC x x--+=-=-，令1r =，则113325(2)10T C x x =-=-，所以3x 得系数为10-．35．【答案】0【解析】∵（1﹣x ）（1+x ）5＝（1﹣x ）（0155C C +•x 25C +•x 235C +•x 345C +•x 455C +•x 5），∴（1﹣x ）（1+x ）5 展开式中x 3的系数为135C ⨯-125C ⨯=0．36．【答案】-80【解析】在52x ⎫⎪⎭的二项展开式中，由展开式通项可得()535215522rrr r rr r T C C x x --+⎛⎫=⋅-=⋅-⋅ ⎪⎝⎭， 令5322r-=-，解得3r =， 所以系数为()()3355428802C ⨯⋅-=⨯-=-， 37．【答案】60【解析】二项式()622x +的展开式通项为：()6212216622rr r r rr r T Cx C x --+=⋅=⋅，取2r，则8x 的系数为226260C ⋅=.38．【答案】20【解析】由题意可得()621231661rrrr rr T Cx C xx --+⎛⎫== ⎪⎝⎭，令333461233,3,20r r T C x x -=∴=∴==，综上所述，3x 的系数为20，故答案为20. 39．【答案】80【解析】由题意52x x ⎛⎫- ⎪⎝⎭的通项公式为()55215522rr r r r r r T C x C x x --+⎛⎫=-=- ⎪⎝⎭，令523r -=-即4r =，则()445280C -=.40．【答案】-80【解析】()5234501234512x a a x a x a x a x a x -=+++++，则()3335280a C =⋅-=-.。

排列组合二项式定理
排列组合二项式定理
知识要点：
1、分类计数原理与分步计数原理
分类的要求
（1）每一类中的每一种方法都可以单独完成此事；
（2）两类不同的方法中的具体方法，互不相同（即分类不重）；
（3）完成此事的任何一种方法，都属于某一类（即分类不漏）。

分步的要求
（1）任何一步中的一种方法都不能完成此事，必须且只须连续走完这几步才能完成此事；
（2）各步计数相互独立，即上一步的不同方法不会影响下一步的方法数；
（3）只要有一步中所取方法不同，则对应完成此事的方法也不同。

2、排列与排列数
（1）捆绑法
（2）插空法
（3）除序法
（4）排除法
（5）穷举法（树图）
（6）特元与特位
3、组合与组合数
（1）两个性质：
（2）挡板法
4、二项式定理
0()n
n r n r r
n r a b C a
b -=+=∑（1）n 次齐次n ＋1项式
（2）最大的二项式系数项居中
（3）通项1r n r r r n T C a b
-+=（4）二项式系数之和
12n n
n n n C C C +++="（5）赋值法求系数和例题与习题：
1．5名运动员参加军事三项赛，射击、游泳、越野长跑各设一名冠军，则三项冠军获得者的结果有多少种？
2．由3枚1分硬币，6枚一角硬币和4张10元纸币，共可组成多少种非零币值？
3．8人排队照相，按如下要求各有多少种不同排队方法？
（1）甲乙丙三人必须相邻、丁戊两人不能相邻.
（2）甲乙两人必站中间，丙丁两人不站两端.
（3）甲不在左端且不在乙的右侧任何位置.
（4）8人中4男4女做到同性别不相邻.。

数学高考总复习：二项式定理编稿：林景飞审稿：张扬责编：严春梅知识网络目标认知考试大纲要求：1．能用计数原理证明二项式定理；2．掌握二项展开式系数的性质及计算的问题；3．会用二项式定理解决与二项展开式有关的简单问题.重点：1．用二项式定理的通项公式解决二项展开式（或多项展开式）中某一项（或某一项的系数）的问题；2．二项展开式中二项式系数的和与各项系数的和问题.难点：1．二项展开式的通项的问题；2．有关多项展开转化为二项展开的问题；3．二项式定理的其他应用问题.知识要点梳理知识点一：二项式定理二项式定理：，其中：①公式右边的多项式叫做的二项展开式；②展开式中各项的系数叫做二项式系数；③式中的第r+1项叫做二项展开式的通项，用表示；二项展开式的通项公式为.知识点二：二项展开式的特性①项数：有n+1项；②次数：每一项的次数都是n次，即二项展开式为齐次式；③各项组成：从左到右，字母a降幂排列，从n到0；字母b升幂排列，从0到n；④系数：依次为.知识点三：二项式系数的性质①对称性：二项展开式中，与首末两端“等距离”的两项的二项式系数相等②单调性：二项式系数在前半部分逐渐增大，在后半部分逐渐减小，在中间取得最大值.其中，当n为偶数时，二项展开式中间一项的二项式系数最大；当n为奇数时，二项展开式中间两项的二项式系数，相等，且最大.③二项式系数之和为，即其中，二项展开式中各奇数项的二项式系数之和等于各偶数项的二项式系数之和，即规律方法指导1．对于二项式定理的构成，展开式中含的项的系数可理解为从n个相同的a+b中先取出r个b，有种不同取法，再从剩下的n-r个括号中取出n-r个a，有种方法，据分步计数原理，共有种不同方法数，该方法数就对应着展开式中含的项的系数.2．二项展开式的各项均含有不同的组合数，若赋予a，b不同的取值，则二项式展开式演变成一个组合恒等式.因此，揭示二项式定理的恒等式为组合恒等式的“母函数”，它是解决组合多项式问题的原始依据.。