(完整版)圆心角,弧,弦,弦心距之间的关系定理知识点及练习,推荐文档

【基础知识精讲】1.基本概念(1)顶点在圆心的角叫圆心角.(2)从圆心到弦的距离叫弦心距.(3)1°的圆心角所对的弧叫1°的弧.2.定理(1)圆是以圆心为对称中心的中心对称图形.(2)在同圆或等圆中，相等的圆心角所对的弧相等，所对的弦相等，所对的弦心距相等.(3)在同圆或等圆中，如果两个圆心角、两条弧、两条弦或两条弦的弦心距中有一组量相等，那么它们所对应的其余各组量分别相等.3.应注意的问题(1)解题时作圆心的弦心距是常用辅助线.(2)等弧的度数一定相等，相等度数的弧不一定是等弧.【重点难点解析】本节的重点是掌握圆心角、弧、弦、弦心距之间的相等关系，并能运用这些关系解决有关的证明、计算题，难点在于选择适当的辅助线，运用这几个量的相等关系解题.例1如图7-20，O是Rt△ABC三条角平分线的交点，∠C=90°，⊙O 经过C点分别交AC、BC于D、E，交AB于F、G，求证⌒CD=⌒CE=⌒FG 证明：作弦CD、CE、FG的弦心距OM、ON、OP，∵O是△ABC的三条角平分线的交点，∴OM=ON=OP ， 则：⌒CD =⌒CE =⌒FG说明：证明弧相等通常证明弧所对的弦或圆周角相等，此题由角平分线定理得三条弦的弦心距相等，从而知道这三条弧相等.图7-20 图7-21 例2 如图7-21，OA 、OB 是⊙O 的两条互相垂直的半径，M 是弦AB 的中点，过M 作MC ∥OA ，交⌒AB 于C ，求证⌒AC =31⌒AB .证明：过M 、C 作ME ⊥AO 于E ，CF ⊥AO 于F ，连OC ∵M 为AB 的中点，∴ME=21OB,易证MEFC 为矩形∴CF=21OB=21OC ，∠COF=30°，则⌒AC =31⌒AB说明：若⌒AC =31⌒AB ，则∠COF=31∠BOA ，由题目条件知，须证明∠COF=30°即可.例3 已知AB 、CD 是⊙O 的两条直径，AP 是⊙O 的弦，且AP ∥CD ，求证BD=DP证明：如图7-22，∵AP ∥CD ，∴⌒AC =⌒PD ， ∵AB 、CD 是两直径，∴∠COA=∠BOD ， ∴⌒CA =⌒BD ，则⌒BD =⌒PD 故BD=DP说明：此题用到“夹在两平行弦之间的弧相等”，“圆心角相等弧相等”，“弧相等弧所对的弦相等”等结论.例4 如图7-23，MBA 与MDC 是⊙O 的二割线，已知弦AB=CD ，求BM=DM. 证明：作OE ⊥AB 于E ，OF ⊥CD 于F ， ∵AB=CD ，∴OE=OF ，则Rt △MEO ≌Rt △MFO ，∴ME=MF ，又AE=21AB=21CD=FC ∴MB=MC说明：本题通过作弦心距将问题转化为证ME=MF ，再通过三角形全等达到目的，在全等的证明过程中用到“弦相等弦心距相等”这一结论. 【难题巧解点拨】例1 如图7-24，⊙O 中弦AB=CD ，⌒AB 与⌒CD 的中点分别是M 和N ，MN 与AB 、CD 分别交于E 和F ，求证：ME=NF.证明：连结AM 、BM 、CN 、DN ∵AB=CD ，∴⌒AB =⌒CD∵M 、N 的分别为⌒AB 、⌒CD 的中点 ∴⌒AM =⌒MB =⌒CN =⌒DN ∴AM=BM=CN=DN ，⌒MD =⌒NB∴∠FND=∠EMB ，∠MBE=∠NDF ，∴△MEB ≌△NFD ，∴ME=FN说明：此题通过弧、弦相等关系的互换证得MB=DN ，从而得△MEB ≌△FND ，得出结论.例2 如图7-25，已知⊙O 的两弦AB 和CD 相交于P ，且∠BPO=∠DPO ，求证：⌒AD =⌒BC .证明：作OE ⊥CD 于E ，OF ⊥AB 于F ， ∵∠BPO=∠DPO ，∴OE=OF ，CD=AB ，⌒AB =⌒CD ，⌒AD =⌒BC说明：本题通过角平分线定理得弦心距相等，从而弦相等，进而弧相等，再去掉公共部分⌒AC 得命题成立.【课本难题解答】1.如图7-26，在⊙O 中，弦AB=CD ，延长AB 到E ，延长CD 到F ，使BE=DF ，求证：EF 的垂直平分线经过点O.分析：由角平分线定理的逆定理知，只须证明OE=OF ，又由条件弦相等得弦心距OM=ON ，从而得△FOM ≌△EON ，证出OF=OE ，命题成立.2.如图7-27，在△ABC 中，∠ACB=90°，∠B=25°，以C 为圆心，CA 为半径的圆交AB 于D ，求⌒AD 的度数.分析：要求弧AD 的度数就是求∠DCA 的度数，由条件易求出∠A=65°，再考虑△CDA ，易求得∠DCA=50°，∴⌒AD =50° 【典型热点考题】例1 如图7-28，已知⊙O 中⌒AB =2⌒CD ，求证明：AB ＜2CD. 证明：取⌒AB 的中心M ，连结BM 、AM ∵⌒AB =2⌒CD ∴⌒AM =⌒BM =⌒CD 从而有AM=BM=CD在△AMB 中，AB ＜BM+AM=2AM=2CD 故AB ＜2CD说明：本题主要考察弦、弧之间的关系，定理告诉我们等弧对等弦，此题告诉我们长不相等的弧的比值与其所对的弦的比值不等.例2 如图7-29，AB 为⊙O 的直径，半径OC ⊥AB ，过OC 的中点D 作弦EF ∥AB ，求证∠ABE=15°.证明：作EH ⊥AB 于H ，则EHOD 为矩形 ∴EH=OD ，又D 为CO 的中点，∴EH=OD=21CO考虑△EHO 知：∠EOH=30°再考虑△EOB 知：∠EBO=21∠EOH=15°例3 在Rt △ABC 中，∠C=90°，∠B=20°，以C 为圆心CA 为半径的圆交BA 于D ，交BC 于E ，求⌒DE 的度数(图7-30).解：连连DC ，考虑△ABC ，∵∠C=90°，∠B=20°∴∠A=70° 考虑△CDA ，∵CD=CA ，∠A=70°∴∠DCA=40°，则∠DCE=50°，∴⌒DE =50° 说明：本题主要考察弧的度数的概念. 本周训练 【同步达纲练习】一、填空题(8分×5=40分)(1)梯形ABCD 内接于⊙O ，且AD ∥BC ，则AB= .(2)AB 、CD 是⊙O 的两弦，E 、F 分别是AB 、CD 的中点，若AB=CD ，作OE= ，∠AOB= ，⌒AB = .(3)圆内最大的弦是12，则这个圆的半径是 . (4)一条弦把圆分成2:3两部分，则劣弧所对的圆心角的度数是 .(5)等边△ABC 内接于⊙O ，则与⌒AB 相等的弧有 ，∠AOB= .二、选择题(8分×5=40分)(1)AB 、CD 分别是两个不等圆的弦，若AB=CD ，则( )A.⌒AB =⌒DCB. ⌒AB ＞⌒DCC. ⌒AB ＜⌒DCD. ⌒AB ≠⌒DC(2)在⊙O 中，⌒AB =2⌒DC ，那么( )A.AB=2DCB.AB=DCC.AB ＜2DCD.AB ＞2DC(3)在△ABC 中，∠A=70°，⊙O 截△ABC 的三边，所截得的弦都相等则∠BOC 等于( )A.11°B.125°C.130°D.不能确定(4)在半径不相等的⊙O 1和⊙O 2中，⌒11B A 与⌒22B A 所对的圆心角都是60°，则下列说法正确的是( )A.⌒11B A 与⌒22B A 的弧长相等 B. ⌒11B A 和⌒22B A 的度数相等C.⌒11B A 与⌒22B A 的弧长和度数都相等 D.⌒11B A 与⌒22B A 的弧长和度数不相等 (5)下面说法正确的是( )A.弦相等，则弦心距相等B.弧长相等的弧所对的弦相等C.垂直于弦的直线必平分弦D.圆的两条平行弦所夹的弧长相等三、解答题(10分×2=20分)(1)从⊙O 外一点P 向⊙O 引两条割线PAB 、PCD 交⊙O 于A 、B 、C 、D ，且⌒AB =⌒CD ，求证：圆心O 必在∠BPD 的平分线上，(2)如图7-31，已知⊙O的半径OA、OB互相垂直，弦AD的延长线交OB 的延长线于C，若∠ACD=32°，求⌒AD的度数.【素质优化训练】1.如图7-32，在⊙O中，弦AB=CD，E、F分别在AB、CD的延长线上，BE=DF，OG⊥EF，垂足为G，求证：G为EF的中点.2.求证：求⊙O内一点A的所有弦中，垂直于OA的弦最短.希望以上资料对你有所帮助，附励志名言3条：1、理想的路总是为有信心的人预备着。

三．圆心角、弧、弦、弦心距之间的关系【知识要点】（1）圆的对称性：圆是以圆心为对称中心的中心对称图形．圆不仅是轴对称图形，而且还是 图形，圆独有的性质是 ． （2）概念：弦、弦心距弦：连结圆上任意两点的线段叫做弦。

经过圆心的弦叫做直线。

直径是圆中最大的弦。

弦心距：圆心到弦的距离叫做弦心距。

【典型例题】例1．（1）过已知⊙O 中一已知点P 的弦中，最短的弦是 ；最长的弦是 ．（2）已知⊙O 中，AB 是直径，长10cm ，点M 为⊙O 内的一点，OM=4cm ，则⊙O 中过点M 的弦中，最长的弦等于 ．（3）在⊙O 中，弦AB ∥弦CD ，且AB 、CD 的度数分别为︒120和︒60，⊙O 的半径为6cm ，则AB 与CD 之间的距离是 ．（4）如图1，⊙O 中，弦CD 与直径AB 交于E ，且∠AEC=︒30，AE=1cm ，BE=5cm ，则弦CD 的弦心距OF= cm ，弦CD 的长为 cm.（3）概念：弧，圆心角弧：圆上任意两点间的部分叫做弧。

弧分为半圆，优弧、劣弧三种。

圆心角 ：顶点在圆心的角叫圆心角，圆心角的度数等于它所对的弧的度数。

例2．（1）如图2，在△ABC 中，︒=∠︒=∠25,90B BCA ，以C 为圆心，CA 为半径的圆交· A C FE ODB 图1· O 图4AB C图2CBDD A图3· OECAB 于D ，则AD 的度数是 ．（2）在⊙O 中，弦AB 与过B 点的半径夹角为︒55，那么弦AB 所对的优弧AMB 的度数为 。

（3）一条弦的弦心距等于它所在圆的直径的41，则这条弦所对的劣弧的度数是 。

（4）已知⊙O 中，AB=2CD ，则弦AB 2CD ．（填“〉”、“〈”或“=” ） （5）如图3所示，已知C 是⊙O 直径AB 上一点，过C 作弦DE ，使CD=CO ，若AD 的度数为︒40，BE 的度数 。

（6）如图4，在⊙O 中，AB 的度数是︒50，∠OBC=︒40，那么∠OAC 等于 。

【注意：同圆或等中】一、知识梳理圆心角，弧，弦，弦心距之间的关系定理：在中，相等的f对的相等,所对的相等，所对的弦的相等.推论：在同圆或等圆中，如果①两个圆心角，②两条弧，③两条弦，④两条弦心距中，有一组量相等,那么它们所对应的其余各组屋都分别相等.eg:在同圆或等圆中，弓玄AB=A f B f,弦心距OD、077,则有:'①(ZA0B=ZA,B,C f)③(4B=48)斗②(佔=AF)®(0D=0,D,)二、讲练结合【圆中相关弦的求解】例1、如图所示，点O是ZEPF的平分线上一点，以O为圆心的圆和角的两边分别交于A.B和C.D,求证：AB=CD.例2、如图，EF为OO的直径，过EF上一点P作弦AB・CD,且ZAPF=ZCPF.求证：PA=PC・VWA例3、如图，OO的弦CE・ED的延长线交于点A,且EC=DE・求证：AC=AE・【巩固练习】1.下列说法中正确的是（）A.相等的圆心角所对的弧相等B.相等的弧所对的圆心角相等C.相等的弦所对的弦心距相等D.弦心距相等，则弦相等2.P为0O内一点，已知OP=lcm,0O的半径r=2cm,则过P点弦中，最短的弦长为（）A・1cmE・JJcmC・cmD・4cm3.在0O中，AE与CD为两平行弦，AE>CD,AB、CD所对圆心角分别为120。

,60。

，若（DO的半径为6,则AB、CD两弦相距（）A・3】B・6C・A/3+1D・3、/J±34.已知：ZAOB=90°,C、D是弧AB的三等分点，AB分别交OC、OD于点E、F・求证：AE=BF=CD・【圆中相关圆心角的求解】例4、如图所示，在AABC中，ZA=72%OO截AABC的三条边长所得的三条弦等长，求ZEOC.1.1,MBC 内接于OO,ZC=45\AB =4则OO 的半径为（A.2>/2 E.4 C.2^3 D ・5 三. 课堂练例5、如图，在0O 中，弓玄AB=CB>ZABC=120°,OD 丄AB 于D,OE 丄EC 于E ・求证：△ODE 是等边三角形.【巩固练习】1. 如图，在0O 中「AB 的度数是50。

圆心 弧 弦 弦心距之间的关系
［知识要点归纳］
1. 圆不但是轴对称图形，而且也是中心对称图形，实际上圆绕圆心旋转任意一个角度，都能够与原来的图形重合。

2. 圆心角：顶点在圆心的角叫做圆心角。

从圆心到弦的距离叫做弦心距。

3. 定理：在同圆或等圆中，相等的圆心角所对的弧相等，所对的弦相等，所对的弦的弦心距相等。

4. 推论：在同圆或等圆中，如果两个圆心角、两条弧、两条弦或两弦的弦心距中有一组量相等，那么它们所对应的其余各组量都分别相等。

5. 1°的弧：因为同圆中相等的圆心角所对的弧相等，所以整个圆也被等分成360份，我们把每一份这样的弧叫做1°的弧。

一般地，n °的圆心角对着n °的弧，n °的弧对着n °的圆心角，也就是说，圆心角的
∴AB ＝CD 弦AB 、DC 若PO 平分∠APC 弦AB 、CD 交于P 点（ PO 平分∠APC
=⎩
OP OP ∴≅∆∆P O M P O N AAS ()
∴=PM PN AM AB CN CD AB CD =
==121
2
，， ∴=AM CN
（）把作出来，变成一段弧，然后比较与的大小。

222CD CD AB ⋂⋂⋂
解法一：
过点作于，则，O OF AB E AF FB AB AE EB AB ⊥⋂=⋂=⋂==121
2
AB CD AE CD AB =∴==21
2
，
AF FB AF FB ⋂=⋂
∴=，（等弧对等弦） 在中，，∆AFB AF FB AB AF AB +>∴>2
∴≅
COF DOE ∆∆
OE OF
∴=。

儒洋教育学科教师辅导讲义6、多边形与圆如果一个圆经过一个多边形的各顶点，那么这个圆叫做这个多边形的外接圆，这个多边形叫做这个圆的内接多边形，提示：1、与圆的确定有关的两个图形一定要学生重点理解。

2、补充两个知识点：线段垂直平分线的性质和角平分线的性质3、和学生一起重点分析课本例题1和2，理解题目考察的细节和解题方法。

二、例题分析：1、以线段AB为弦的圆的圆心的轨迹是＿＿＿＿＿＿＿＿＿＿＿。

cm。

2、已知扇形的圆心角为120°，半径为2cm，则扇形的弧长是cm，扇形的面积是23、点和圆的位置关系有三种：点在圆，点在圆，点在圆；例1：已知圆的半径r等于5厘米，点到圆心的距离为d，（1）当d=2厘米时，有d r，点在圆（2）当d=7厘米时，有d r，点在圆（3）当d=5厘米时，有d r，点在圆4、下列四边形：①平行四边形，②菱形；③矩形；④正方形。

其中四个顶点一定能在同一个圆上的有（）A、①②③④B、②③④C、②③D、③④5、（07上海中考）小明不慎把家里的圆形玻璃打碎了，其中四块碎片如图所示，为配到与原来大小一样的圆形玻璃，小明带到商店去的一块玻璃碎片应该是（）A．第①块 B．第②块C．第③块 D．第④块6、三角形的外接圆的圆心是（），A．三条中线的交点B．三条高的交点C．三条角平分线的交点D．三条边的垂直平分线的交点7、直角三角形的两条直角边分别为5cm和12cm，则其外接圆半径长为。

（三）巩固练习1、圆是轴对称图形，其对称轴是任意一条的直线；圆是中心对称图形，对称中心为．2、三角形的外接圆的圆心——三角形的外心——三角形的交点；三角形的内切圆的圆心——三角形的内心——三角形的交点；3、三角形的外心一定在该三角形上的三角形（）（A）锐角三角形（B）钝角三角形（C）直角三角形（D）等腰三角形，第7题 （第2题） 7、如图，AB 和DE 是⊙O 的直径，弦AC ∥DE ，若弦BE=3，则弦CE=_______8、如图，OE ⊥AB 、OF ⊥CD ，如果OE=OF ，那么_______（只需写一个正确的结论）B A CEDOF（第8题） （第11题）9、已知，如图所示，点O 是∠EPF 的平分线上的一点，以O 为圆心的圆和角的两边分别交于点A 、Ｂ和C 、D 。

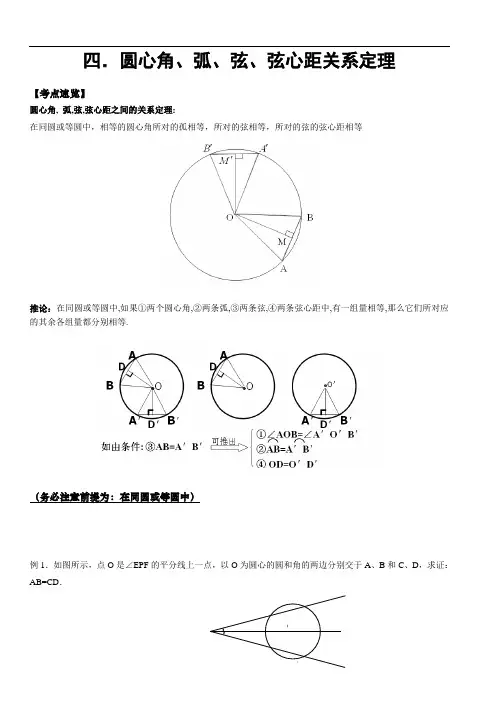
四．圆心角、弧、弦、弦心距关系定理【考点速览】圆心角, 弧,弦,弦心距之间的关系定理:在同圆或等圆中，相等的圆心角所对的孤相等，所对的弦相等，所对的弦的弦心距相等推论：在同圆或等圆中,如果①两个圆心角,②两条弧,③两条弦,④两条弦心距中,有一组量相等,那么它们所对应的其余各组量都分别相等.（务必注意前提为：在同圆或等圆中）例1．如图所示，点O是∠EPF的平分线上一点，以O为圆心的圆和角的两边分别交于A、B和C、D，求证：AB=CD．ABE OOPO 1O 2O例2、已知：如图，EF 为⊙O 的直径，过EF 上一点P 作弦AB 、CD ，且∠APF=∠CPF 。

求证：PA=PC 。

例3．如图所示，在ABC ∆中，∠A=︒72，⊙O 截ABC ∆的三条边长所得的三条弦等长，求∠BOC.例4．如图，⊙O 的弦CB 、ED 的延长线交于点A ，且BC=DE ．求证：AC=AE ．·OAB CO ·CAEBD例5．如图所示，已知在⊙O 中，弦AB=CB ，∠ABC=︒120，OD ⊥AB 于D ，OE ⊥BC 于E ． 求证：ODE ∆是等边三角形．综合练习一、选择题1．下列说法中正确的是（ ）A 、相等的圆心角所对的弧相等B 、相等的弧所对的圆心角相等C 、相等的弦所对的弦心距相等D 、弦心距相等，则弦相等2．如图，在⊙O 中，AB 的度数是︒50，∠OBC=︒40，那么∠OAC 等于（ ） A 、︒15 B 、︒20 C 、︒25 D 、︒303．P 为⊙O 内一点，已知OP=1cm ，⊙O 的半径r=2cm ，则过P 点弦中，最短的弦长为（ ） A 、1cm B 、3cm C 、32cm D 、4cm4．在⊙O 中，AB 与CD 为两平行弦，AB >CD ，AB 、CD 所对圆心角分别为︒︒60,120，若⊙O 的半径为6，则AB 、CD 两弦相距（ ）A 、3B 、6C 、13+D 、333± 5.如图所示，已知△ABC 是等边三角形，以BC 为直径的⊙O 分别交AB 、AC 于点D 、E 。

圆心角、弧、弦、弦心距之间的关系一、基本知识点总结[构成] 圆心角顶点在圆心，两边与圆相交的角弧圆上任意两点间的部分弦连接圆上任意两点的线段弦心距从圆心到弦的距离[圆心角] 同圆或等圆中，相等的圆心角所对的弧相等，所对的弦相等，所对的弦心距也相等[ 弧 ] 同圆或等圆中，相等的弧所对的圆心角相等，所对的弦相等，所对的弦心距也相等[ 弦 ] 同圆或等圆中，相等的弦所对的圆心角相等，所对的弧相等，所对的弦心距也相等[弦心距] 同圆或等圆中，相等的弦心距所对的弦相等，所对的现所对的圆心角和弧也相等[ 对称 ] 圆是以圆心为对称中心的中心对称图形二、知识的应用1、以点O为圆心的两个同心圆，大圆的弦AB交小圆于C、D，如果AB=3cm，CD=2cm，那么AC=_____ cm。

（应当画图分析得之）2、在⊙O中，弦AB的为8cm，AB弦的弦心距的长为3cm，则⊙O的半径长为（）A、7 cmB、5 cmC、7 cmD、73cm3、在⊙O中，弦AB垂直并且平分一条半径，则劣弧AB的度数等于［］A.30°B.120°C.150°D.60°4、如图在圆O中，弦AB将弦CD分成1：3的两部分，且PA*PB=9，则CD= 。

（A）5、已知如图在圆0中，弦AB与半径OC相交于点M，且OM=MC，若AM=1.5，BM=4，则OC的长为。

(B)6、如图PT切⊙O于点T，PA交⊙O于点A、B，且与直径CT相交于点D，CD=2，AD=3，BD=6，则PB= 。

7、在⊙O 中，AB 是直径，弦CD 与AB 相交于点E ，若 ，则CE=DE （只需填一个适合的条件）。

8、如图，⊙O 中，弦AB⊥弦CD 于E ，OF⊥AB 于F ，OG⊥CD 于G ，若AE=8cm ，EB=4cm ，则OG= cm 。

9、已知：如图，在⊙O 中，CD 为弦，A 、B 两点在CD 的两端延长线上，且AC=BD 。

专题09 圆心角、弧、弦、弦心距之间的关系（3个知识点3种题型）【目录】倍速学习四种方法【方法一】脉络梳理法知识点1.圆心角、弧、弦、弦心距等概念知识点2.圆心角、弧、弦、弦心距之间的关系的推论知识点3.圆心角、弧、弦、弦心距之间的关系定理及推论的综合运用【方法二】实例探索法题型1.圆心角、弧、弦、弦心距之间的关系的定理题型2.圆心角、弧、弦、弦心距之间的关系的推论题型3.圆心角、弧、弦、弦心距之间的关系的定理及推论的综合运用【方法三】成果评定法【倍速学习五种方法】【方法一】脉络梳理法知识点1.圆心角、弧、弦、弦心距等概念圆上任意两点之间的部分叫做圆弧，简称弧．2．联结圆上任意两点的线段叫做弦．过圆心的弦就是直径．3．以圆心为顶点的角叫做圆心角．4．圆的任意一条直径的两个端点将圆分成两条弧，每一条弧都叫做半圆．5．大于半圆的弧叫做优弧，小于半圆的弧叫做劣弧．6．圆心到弦的距离叫做弦心距．【例1】（2023·九年级课时练习）图中是圆心角的是（ ）A．B．C．D．知识点2.圆心角、弧、弦、弦心距之间的关系的推论推论：在同圆或等圆中，如果两个同心角、两条劣弧（或优弧）、两条弦、两条弦的弦心距得到的四组量中有一组量相等，那么它们所应的其余三组量也分别相等．【例2】（2023·江苏苏州·九年级苏州工业园区星湾学校校考期中）如图，点,,,A B C D 在O e 上，且 AB DC=，判断AC 与BD 的数量关系．知识点3.圆心角、弧、弦、弦心距之间的关系定理及推论的综合运用1．定理：在同圆或等圆中，相等的圆心角所对的弧相等，所对的弦相等，所对的弦的弦心距相等．2．推论：在同圆或等圆中，如果两个同心角、两条劣弧（或优弧）、两条弦、两条弦的弦心距得到的四组量中有一组量相等，那么它们所应的其余三组量也分别相等．【例3】（2023·山东潍坊·九年级统考期中）下列说法正确的是（ ）A ．度数相等的弧所对的圆心角相等B ．相等的圆周角所对弧的度数相等C ．圆周角的度数等于圆心角度数的一半D ．三角形的外心到三角形各边的距离相等【变式】（2023·浙江宁波·九年级校联考阶段练习）如图，AB 是O e 的直径，C ，D 在⊙O 上，且位于AB异侧， BC ， AD 的度数分别为60°，100°，请仅用直尺按要求作图．(1)画出一个大小为30°的角，并写出该角．(2)画出一个以AD 为腰的等腰三角形，并写出该等腰三角形．【方法二】实例探索法题型1.圆心角、弧、弦、弦心距之间的关系的定理1.（2023·九年级课时练习）如图所示，四边形ABCD 内接于O e ，50,25,65B ACD BAD Ð=°Ð=°Ð=°．求证：(1)AD CD =；(2)AB 是O e 的直径．2.（2023·北京朝阳·九年级校考期中）如图，点A 、B 、C 、D 在O e 上，AD BC =，AB 与CD 相等吗？为什么？题型2.圆心角、弧、弦、弦心距之间的关系的推论3.（2023·江苏常州·九年级校考阶段练习）下列说法正确的是（ ）A ．相等的圆心角所对的弧相等B ．圆周角等于圆心角的一半C ．等弧所对的弦相等D ．平面内三点确定一个圆题型3.圆心角、弧、弦、弦心距之间的关系的定理及推论的综合运用(1)求证AC BD =；(2)连接CD ，若30BDC Ð=【方法三】 成果评定法一、单选题1．（2021·河北石家庄·九年级石家庄市第九中学校考期中）圆内接四边形ABCD 中，A B C ÐÐÐ，，的度数之比为2:5:7，则D Ð的度数为（ ）A ．60°B ．80°C ．100°D ．120°2．（2023·浙江杭州·九年级校联考期中）如图，AB 是O e 的直径，点C 在圆上，若 64CB°=，则CBA Ð的度数为（ ）A ．32°B ．64°C ．68°D ．58°3．（2023·江苏苏州·九年级苏州工业园区星湾学校校考期中）如图，点A ，B ，C ，D 在O e 上，142AOC Ð=°，点B 是 AC 的中点，则D Ð的度数是（ ）A ．70°B ．55°C ． 35.5°D ．35°4．（2023·浙江杭州·九年级统考期中）如图，已知BC 是O e 的直径，半径OA BC ^，点D 在劣弧 AC 上（不与点A ，点C 重合），BD 与OA 交于点E ，设,AED AOD a b Ð=Ð=，则（ ）A ．2180a b +=°C ．3180a b +=°5．（2023·浙江·九年级校联考期中）如图，在折，交AB 于点D （不与点OA ．44°6．（2023·福建厦门90ADC Ð=°，DA A ．33-B ．5二、填空题7．（2023·北京朝阳·九年级校考期中）如图，用直角曲尺可以检查半圆形的工件是否合格，其中的数学依8．（2021·山东泰安·九年级统考期末）如图，将一块含30°角的直角三角板的锐角顶点9．（2023·江苏宿迁·九年级统考期中）如图，正六边形10．（2023·北京朝阳·九年级校考期中）已知23O O e e ，上．如图，①以C 为圆心，AP 长为半径作弧交②以E 为圆心，BP 长为半径作弧交11．（2023·江苏镇江·九年级统考期中）如图，ABC V 为 ．13．（2023·内蒙古通辽角度数是14．（2023·江苏盐城15．（2023·广东汕头·九年级校考阶段练习）如图，а，D为弧CAB=30为16．（2023·广西南宁·九年级广西大学附属中学校考阶段练习）如图，圆内接四边形Ð=°，连接OB，BCD10518．（2023·浙江宁波·九年级校联考阶段练习）如图，点，120APB Ð=°，若三、解答题19．（江苏省宿迁市洋河新区教学共同体2023-2024学年九年级上学期期中数学试题）如图，图中两条弦AB CD 、相交于点E ，且AE DE =，求证：AB CD =．20．（2022·江苏南京·九年级统考期末）如图，在O e 中，弦AB CD 、的延长线交于点P ，且DA DP =．求证：BC BP =．21．（2023·浙江杭州·九年级杭师大附中校考期中）如图，弦DB EC ，的延长相交于圆外一点A ，连结C D ，B E ．(1)求证：ACD ABE ∽△△；(2)若5AB =，6AC =，10AE =，求AD 的长．22．（2023·湖北武汉·九年级统考期中）如图，四边形ABCD 内接于O e ，AC 为O e 的直径，B 为 AC 的中点．(1)试判断ABC V 的形状，并说明理由；(2)若6AD CD +=，求BD 的长．23．（2023·吉林·九年级吉林松花江中学校考期中）如图，AB 为O e 的直径，弦CD 与AB 交于点E ，连接AC 、BD ，=75C а；=45D а．(1)求AEC Ð的度数；(2)连接OC ，若=2AC ，则O e 的半径为_____．(1)不添其他辅助线写出图中一对相似三角形，并说明理由；(2)求弦CE的长．。