2423圆心角弧弦弦心距之间的关系精品PPT课件

格式：pptx
大小：507.67 KB
文档页数：59

下载文档原格式

3.2圆心角、弧、弦、弦心距之间的关系课件

A

C
O B
AB = CD
？！

O'
在同圆或等圆中，相等的圆心角所对的弧相等，所对的弦相等
D
圆心角、弧、弦、弦心距之间的关系
在自己的圆内作两条长度相同的弦，量一量它们所对的圆心角
D B C
B O A
O'
B' A'
O A
圆心角、弧、弦、弦心距之间的关系
D B C
B O A O'
同圆
同一个圆
O
等圆
半径相等的两个圆同圆或等圆的半径相等
O
O'
圆心角、弧、弦、弦心距之间的关系
B A
圆心角:
顶点在圆心，两边与圆相交的角.
O C
∠AOB ∠AOC
∠COD
∠BOD
D
圆心角、弧、弦、弦心距之间的关系
D
弦连接圆上两点的线段. 等弦长度相等的两条弦.
C
弧圆上两点之间的部分.
A B
O
D
圆心角、弧、弦、弦心距之间的关系
在同圆或等圆中，如果两个圆心角、两条弧、两条弦、两条弦的弦心距中有一组量相等，那么它们所对应的其余各组量都分别相等. 我们可以利用这个定理，证明角相等、弧相等、弦相等
作业：
课本 P 107 1、2、3
《作业本》相关内容
遇到困难不要抱怨，既然改变不了过去，那就改变未来。
§3.2 圆心角、弧、弦、弦心距之间的关系
圆心角、弧、弦、弦心距之间的关系
圆是轴对称图形
O
对称轴是任意一条过圆心的直线圆是中心对称图形对称中心为圆心
我们已经学过的图形中，有哪些既是轴对称图形，又是中心对称图形？

【沪科版】2017版九年级下册：24.2.3《圆心角弧弦弦心距之间的关系》ppt课件

n°的圆心角
C
O
n°
B A
n°的弧
1°的圆心角
1°的弧
例4已知:等边三角形ABC的三个顶点都在⊙O上, 求证:∠AOB=∠BOC=∠AOC=120°
例5.已知:点O是∠PAQ平分线上的一点,⊙O分别交∠A两边于点C,D和点O分别交∠PAQ 的两边于C,D,E,F,且CD=EF。求证:AO平分∠PAQ。
二、学习目标：
1、掌握圆心角定义，理解并掌握圆心角，弧，弦，弦心距之间的关系 2、理解并掌握圆心角的度数与它所对的弧的度数之间的关系。 3、能利用圆心角、弧、弦、弦心距之间的关系解决有关的证明与计算问题。
三、自学提纲：
看书本上第18-19页内容，解决以下问题:
1.什么叫圆心角？ 2.圆心角，弧，弦，弦心距之间的相等关系定理及其推论的内容是什么？怎样用符号语言来表述？ 3.圆心角的度数等于它所对弧的度数吗？ 4.阅读书本上例4、5、6.掌握解题方法与解题步骤。
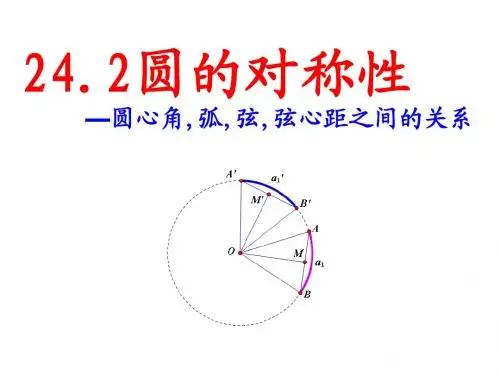
24.2圆的对称性
—圆心角,弧,弦,弦心距之间的关系
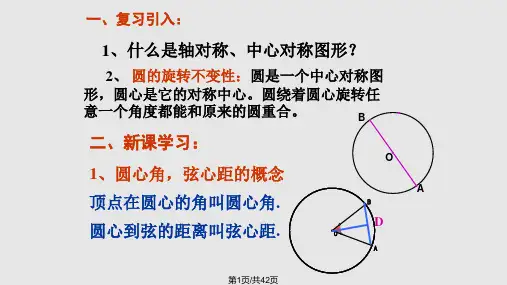
一、复习引入：
1.圆的对称性有哪些? 2.垂径定理、垂径定理的推论的内容各是什么? 3.什么叫弦心距? 4.你学过的与圆有关的第一条辅助线是什么? 圆不仅是轴对称图形,中心对称图形, 而且还有旋转不变性. 本节课,我们来学习根据圆的旋转不变性得到的圆心角,弧,弦,弦心距之间的一些性质.
M
Q
︵例6.已知:AB,CD为⊙O的两条直径,弦CE∥BA，EC 为40°,求∠BOD的度数.
五、巩固新知，当堂训练
1、填一填,练一练:
已知：如图，AB、CD是⊙O的两条弦，OE、OF为AB、CD的弦心距，根据本节定理及推论填空：（1）如果AB=CD，那么______。

24.2.3圆心角、弧、弦、弦心距之间的关系PPT课件

D
①∠AOB=∠A′O′B′
B
●O
可推出 ⌒ ⌒ ②AB=A′B′
┏
A′ D′ B′
④ OD=O′D′
第14页/共30页
试一试你的能力
一.判断下列说法是否正确：
1相等的圆心角所对的弧相等。（ ×）
2相等的弧所对的弦相等。（ √ ）
B
二.如图，⊙O中，AB=CD,
1A
1 50，则 2 _5_0_o_.
解: ∵ AC=BD （已知）
∴ AC-BC=BD-BC （等式的性质）
∴ AB=CD
图 23.1.5
∴ ∠1=∠2=45° （在同圆中，相等的弧所对的圆心角相等）
第27页/共30页
六、练习
如图，AB是⊙O 的直径，BC = CD = DE
∠COD=35°，求∠AOE 的度数．
解：
ED
∵ BC = CD = DE
两位同学先作一个度数相同的圆心角！
B
O
A
B'
O'
A'
这两个相等的圆心角所对的弦分别是哪两条？它们相等吗？用尺量一量！
这两个相等的圆心角所对的弧分别是哪两条？
它们相等吗？用什么方法验证的?
叠合法
第5页/共30页
二、
探究
如图，将圆心角∠AOB绕圆心O旋转到∠A’OB’的位置，你能发现哪些等量关系？为什么？
︵︵
AB A' B '.
AB A' B '.
第6页/共30页
圆心角、弧、弦、弦心距之间的关系
A
D B
O
B'
B
B'
D'

圆心角弧弦弦心距之间的关系省名师优质课赛课获奖课件市赛课一等奖课件

B′
A′ B
B′
·
O
A
·
O
A
根据旋转旳性质，将圆心角∠AOB绕圆心O旋转到∠A′OB′旳
位置时， ∠AOB＝∠A′OB′，射线 OA与OA′重叠，OB与OB′重
叠．而同圆旳半径相等，OA=OA′，OB=OB′，∴点 A与 A′重
叠，B与B′重叠．
∴A︵B与
︵
A'B
'
.
重叠，AB与A′B′重叠．
︵︵
AB A' B '.
O B'
（2）在⊙O和⊙O’中，假如
A'
B
︵︵ AB=A’B’,那么AB=A`B`.
A
（不对）
圆心角、弧、弦、弦心距之间旳关系
(1)定理：在同圆中，相等旳圆心角所正确弦相等，所正确弧相等，所正确弦心距相等。
思索定理旳条件和结论分别是什么？并回答：
条件：在等圆或同圆中圆心角相等
结论：
演示
圆心角所对弧相等
∴ AC-BC=BD-BC （等式旳性质）图 23.1.5 ∴ AB=CD ∴ ∠1=∠2=45° （在同圆中，相等旳弧所正确
圆心角相等）
六、练习
如图，AB是⊙O 旳直径，BC = CD = DE ∠COD=35°，求∠AOE 旳度数．
解：
ED
∵ BC = CD = DE
C
BOC=COD=DOE=35
1A
1 50，则 2 _5_0_o_ .
C 2O
D
四、练习
如图，AB、CD是⊙O旳两条弦．（1）假如AB=CD，那么__A ___B __=___C _，D _______A_O_B_____C__O_D．

沪科版九年级下数学《24.2.3圆心角、弧、弦、弦心距间关系》课件

讲授新课
一圆的对称性
观察与思考把圆绕圆心旋转任意一个角度，仍与原来的圆重合吗？
α
·
O
圆是旋转对称图形，具有旋转不变性，旋转中心为圆心.
二圆心角
概念学习
1. 圆心角：顶点在圆心的角叫做圆心角，如∠AOB .
2. 圆心角 ∠AOB 所对的弧为 A⌒B.
B
3. 圆心角 ∠AOB所对的弦为AB.
M
（√ ）
(3) 圆心角相等，所对的弦相等. （ × ）
四关系定理及推论的运用
典例精析
例1 如图，等边三角形 ABC 的三个顶点都在☉O上. 求证：∠AOB=∠BOC=∠COA=120°.
证明：连接OA，OB，OC，如图.
A
∵ AB=BC=CA，
∴∠AOB =∠BOC =∠COA = 1 360 =120 . 3
AB
成立.理由如下：
取 C⌒D 的中点 E，连接 OE，CE，
C
DE ，那么∠AOB=∠COE =∠DOE，
O
E
所以 AB = CE = DE ，CD =2 AB ，
弦AB = CE = DE，
D
在△CDE中，CE+DE > CD，即 CD ＜ 2AB.
课堂小结
圆心角
弦、弧、圆心角的关系定理
概念：顶点在圆心的角
不可以，如图.
B D OC A
在☉O中，如果 A⌒B=C⌒D，那么圆心角∠AOB与 ∠COD，AB与CD，OE=OF有怎样的数量关系？
在☉O中，如果AB=CD，那么圆心角∠AOB与
∠COD，A⌒B与C⌒D，OE=OF有怎样的数量关系？
在☉O中，如果OE=OF，那么圆心角∠AOB与

圆心角、弧、弦、弦心距之间的关系 ppt课件

2
精品资料
• 你怎么称呼老师？ • 如果老师最后没有总结一节课的重点的难点，你
是否会认为老师的教学方法需要改进？ • 你所经历的课堂，是讲座式还是讨论式？ • 教师的教鞭 • “不怕太阳晒，也不怕那风雨狂，只怕先生骂我
笨，没有学问无颜见爹娘 ……” • “太阳当空照，花儿对我笑，小鸟说早早早……”
如图：
A
AOB= COD
B
o
C
D
ppt课件
12
下面我们一起来观察一下圆心角与它所对的弦、弧有什么关系？
如图：
A
AOB= COD
B
o
C
D
ppt课件
13
下面我们一起来观察一下圆心角与它所对的弦、弧有什么关系？
如图：
A
AOB= COD
B
o
C
D
ppt课件
14
下面我们一起来观察一下圆心角与它所对的弦、弧有什么关系？
如图：
A
AOB= COD
B
o
C
D
ppt课件
18
下面我们一起来观察一下圆心角与它所对的弦、弧有什么关系？
A
如图： ∠AOB=∠COD
B
o
C
D
ppt课件
19
A
把扇形COD绕点O旋转，使OC
B
与OA重合，因∠AOB=∠COD,
所以OD与OB重合，而圆O的半径相等，因此点C与点A重合，点D与点B重合，这样A⌒B 与C⌒D
弦AB和弦ＣＤ对应的弦心距什么关系？
A Ｅ B
o
C Ｆ D
ppt课件
22
ppt课件
23
ppt课件
24

圆心角弦弦心距之间的关系PPT课件

O
O
①
②
O
O
③
④
第2页/共42页
圆心角、弧、弦、弦心距之间的关系
(1)定理：在同圆中，相等的圆心角所对的弦
相等，所对的弧相等，所对的弦心距相
等。
思考定理的条件和结论分别是什么？并回答：
条件：
结论：演示
在等圆或同圆中圆心角所对弧相等
圆心角相等
圆心角所对弦相等圆心角所对的弦心距相等
猜想：把圆心角相等与三个结论的任何一个交换位置，有怎样的结果？
倍，c
O
A
E
B
C
13、如图，在⊙O 中，弦AB、CD相交于点P，OM⊥CD， ON⊥AB，M、N是垂足，联结MN，如果AD=BC，求证：△PMN是等腰三角形。
第40页/共42页
第41页/共42页
感谢您的欣赏
第42页/共42页
已知：如图，AB，CD是⊙O的两条弦，A OE、OF为AB、CD的弦心距，根据这
D O
F
节课所学的定理及推论填空：
C
(1)如果∠AOB=∠COD，那么 OE=OF ，AB=CD，A⌒B=C⌒D ; (2)如果OE=OF，那么 ∠AOB=∠CO，D AB=CD， A⌒B=C⌒D；
(3)如果A⌒B=C⌒D，那么 ∠AOB=∠COD， AB=CD， OE=OF；
变式1：
A
B
M O·
N
D C
第8页/共42页
C E
A
B
M O
•
P N
变式2：
已知：如图， ⊙O的弦AB，CD相交于点P，APO=∠CPO
F 求证：AB=CD
D
第9页/共42页
变式3：

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

A
P
O·
C
N
∴ OM⊥AB ∴ ON⊥CD
D
∴ OM＝ON
∴AB＝CD
例1：如图，点O是∠EPF平分线上的一点，以O为圆心的圆和角
的两边分别交于点A、B和C、D
求证：AB=CD B
M
A
P
O·
C
N
D
B CE
M •O PN
变式2：
已知：如图，
⊙O的弦AB， CD相交于点P， APO=∠CPO F 求证：AB=CD
（4）如果AB=CD，OE⊥AB于E，OF⊥CD于F，OE与OF相等吗？为什么？ OE﹦OF
证明：∵ O﹦CD ∴ AE﹦CF
O·
D
∵ OA﹦OC ∴ Rt△AOE≌Rt △COF
F
∴ OE﹦OF
C
五、例题
例1 如图，在⊙O中， AB = 求证∠AOB=∠BOC=∠AOC
2相等的弧所对的弦相等。（ √ ）
B
二.如图，⊙O中，AB=CD,
1A
1 50，则 2 _5_0_o_ .
C 2O
D
四、练习
如图，AB、CD是⊙O的两条弦．（1）如果AB=CD，那么__A ___B __=___C _，D _______A_O_B_____C__O_D．
（2）如果 AB= CD，那么____A__B_=__C_D__，____A__O_B______C．OD （3）如果∠AOB=∠COD，那么___A __B __= ___C ___D ，____A__B_=__C．D
24.2.3圆的对称性
圆心角、弧、弦、弦心距之间的关系
圆心角、弧、弦、弦心距之间的关系
同圆
重合的两个圆
O
等圆
半径相等的两个圆
同圆或等圆的半径相等
O O'
圆心角、弧、弦、弦心距之间的关系
D
弦
C
弧
A
B
等弧
在同圆或等中，能够互相重合的两条弧叫做等弧
B
如图：以圆心O为顶点作一个
角，这个角的两边与圆O相交，
在同圆或等圆中，相等的弧所对的圆心角 _相__等__，所对的弦___相__等___；
在同圆或等圆中，相等的弦所对的圆心角 __相__等__，所对的弧____相__等___．
同圆或等圆中，两个圆心角、两条弧、两条弦、两条弦的弦心距中有一组量相等，它们所对应的其余各组量也相等．
➢ 在同圆或等圆中,如果①两个圆心角,
条件：在等圆或同圆中圆心角相等
结论：
演示
圆心角所对弧相等
圆心角所对弦相等圆心角所对的弦心距相等
猜想：把圆心角相等与三个结论的任何一个交换位置，有怎样的结果？
圆心角、弧、弦、弦心距之间的关系
在自己的圆内作两条长度相同的弦，量一量它们所对的圆心角
D B
C O A
圆心角、弧、弦、弦心距之间的关系
两位同学作一条长度相同的弦，看一看它们所对的圆心角是否相同
B
O
A
B'
O'
A'
(2) 推论：在同圆或等圆中,如果两个圆心角、两条弧、两条弦或两条弦的弦心距中有一组量相等，
那么它们所对应的其余各组量都分别相等。
A
D B
O
B' D' A'
三、定理
弧、弦与圆心角的关系定理
在同圆或等圆中，相等的圆心角所对的弧相等，所对的弦也相等，所对的弦心距相等。
A′
B
B′
A′ B
B′
·
O
A
·
O
A
根据旋转的性质，将圆心角∠AOB绕圆心O旋转到∠A′OB′的
位置时， ∠AOB＝∠A′OB′，射线 OA与OA′重合，OB与OB′重
合．而同圆的半径相等，OA=OA′，OB=OB′，∴点 A与 A′重
合，B与B′重合．
∴A︵B与
︵
A'B
'
.
重合，AB与A′B′重合．
推 ➢ ②两条弧,③两条弦,④两条弦心距中, 论 ➢ 有一组量相等,那么它们所对应的
➢ 其余各组量都分别相等.
A
D
B
●O
如由条件: ③AB=A′B′ ①∠AOB=∠A′O′B′
可推出 ⌒ ⌒ ②AB=A′B′
┏
A′ D′ B′
④ OD=O′D′
试一试你的能力
一.判断下列说法是否正确：
1相等的圆心角所对的弧相等。（ ×）
证明：
AC ,∠ACB=60°,
A
∵ AB = AC
∴ AB=AC．又∠ACB=60°，
O·
B
C
∴ AB=BC=CA.
∴ ∠AOB＝∠BOC＝∠AOC.
例1：如图，点O是∠EPF平分线上的一点，
以O为圆心的圆和角的两边分别交于点A、B
和C、D 求证：AB=CD
证明：作OM⊥AB，
B M
ON⊥CD，M、N为垂足， ∵ ∠MPO=∠NPO
如果设这个角是∠ＡＯＢ，那么OA、OB分别与⊙O相交于点
┌M O
Ａ与点Ｂ
A
(
顶点在圆心的角称为圆心角，把以点Ａ和点 B的端点的弧AB称为圆心角∠ＡＯＢ所对的弧，把象ＯＭ这样的以圆心Ｏ到弦ＡＢ的距离称为弦ＡＢ的弦的弦心距．
练习：判别下列各图中的角是不是圆心角，并说明理由。
O
O
①
②
O
O
③
④
圆心角、弧、弦、弦心距之间的关系
︵︵
AB A' B '.
AB A' B '.
圆心角、弧、弦、弦心距之间的关系
A
D B
B'
B
O D' O
A
A'
B'
O'
A'
前提条件
在同圆或等圆中，
相等的圆心角所对的弧相等，所对的弦相等，所对的弦心距相等
三、巩固应用、变式练习
1 、判断题，下列说法正确吗？为什么？
（1）如图：因为∠AOB=∠A’OB’，
A
变式1：
B
M
A
·O
D
N
C
变式3：如图M、N为AB、
CD的中点,且AB=CD. 求证：∠AMN＝∠CNM
AC
M• N O
B D
三、基础练习：
A⌒mB
1、一条弦把圆分成3：6两部分，则优弧所对
的圆心角为 240 °.
2、A、B、C为⊙O上三点，若 A⌒B 、B⌒C 、C⌒D 的度数之比为1：2：3，
则∠AOB= 60 °，
∠BOC= 120 °, ∠COA= 180 °.
3、在⊙O中，AB弧的度数为60°，AB弧的长
︵︵所以AB=A`B`. （不对）
O B'
（2）在⊙O和⊙O’中，如果
A'
B
︵︵ AB=A’B’,那么AB=A`B`.
A
（不对）
圆心角、弧、弦、弦心距之间的关系
(1)定理：在同圆(或等圆)中，相等的圆心角所对的弦相等，所对的弧相等，所对的弦心距相等。
思考定理的条件和结论分别是什么？并回答：
在等圆中
两位同学先作一个度数相同的圆心角！
B
O
A
B'
O'
A'
这两个相等的圆心角所对的弦分别是哪两条？它们相等吗？用尺量一量！
这两个相等的圆心角所对的弧分别是哪两条？
它们相等吗？用什么方法验证的?
叠合法
二、
探究
如图，将圆心角∠AOB绕圆心O旋转到∠A’OB’的位置，你能发现哪些等量关系？为什么？