有效折射率法求矩形波导色散曲线(附Matlab程序).doc
- 格式:doc
- 大小:699.33 KB
- 文档页数:13

色散关系的matlab
色散是光学中一项重要的现象,指的是不同波长光在传播过程中
速度不同,导致光束发生弯曲或分散的现象。
色散关系描述了光在介
质中传播过程中波长与相速度之间的关系。
因此,了解色散关系对于
研究光学现象和设计光学器件有着重要意义。
MatLab是一种常用的计算机编程语言,可以用于实现多种科学计算和数据分析操作。
通过编写MatLab程序,可以计算和绘制色散关系
曲线。
在编写色散关系的MatLab程序中,需要考虑介质的折射率与波
长的关系,以及折射率对相速度的影响。
一般来说,介质的折射率与
波长呈现非线性关系,这也是导致色散的主要原因。
因此,在计算色
散关系时需要使用非线性函数来描述介质的折射率随波长变化的曲线。
对于不同的介质,其色散关系曲线可能具有不同的特点。
例如,
某些介质的色散关系可能在某个波长附近出现弯曲,导致光束的聚焦
效果较好;而其他的介质则可能在整个波长范围内表现出较强的色散
效应,导致光束发生相对较大的分散。
通过MatLab编写色散关系程序,可以方便地进行多组实验数据
的处理、展示和比较。
同时,由于MatLab具有高效性和可扩展性,用
户还可以对程序进行进一步的优化,加入更多的计算模型或者实验数据,以实现更精确和全面的分析和表达。
总之,MatLab编写的色散关系程序可以为研究和应用光学现象提供有力支持和帮助,对于学术研究和工程应用均有着重要的意义。

matlab矩形波Matlab矩形波是一种经典的信号模型,通常用于数字信号处理和模拟电路设计中。
本文将从简单到复杂,逐步讲解如何在Matlab中生成矩形波,并探讨其一些简单的应用。
这里先定义矩形波的数学表达式:$rect(x)= \begin{cases} 1, &|x| < \frac{1}{2} \\ 0, &\text{其他} \end{cases}$,其中$x$为自变量。
可以看到,矩形波在以$\frac{1}{2}$为半长的区间内取值为1,其他地方取值为0。
在Matlab中,我们可以使用以下代码生成矩形波:```matlabt = -5:0.01:5; %定义自变量t的取值范围y = rect(t); %用自定义的rect函数生成对应的矩形波yplot(t,y); %用plot函数将t和y作图xlabel('t'); ylabel('y');title('矩形波'); %添加横轴和纵轴标签,以及图像标题```这段代码中用到了自定义的rect函数,它的具体实现如下:```matlabfunction y = rect(x)y = zeros(size(x));y(abs(x) < 0.5) = 1;end```该函数接受一个实参$x$,返回与之对应的矩形波$y$。
在函数中,首先用zeros函数创建一个与$x$相同大小的全零数组$y$。
然后根据矩形波的数学表达式,将$|x|$小于0.5的元素赋值为1。
最后返回数组$y$。
通过上述代码,在Matlab中就可以生成矩形波,并将其可视化。
下面我们将扩展其一些简单应用。
首先是频率分析。
在信号处理中,我们通常需要分析信号的频域特性。
对于矩形波来说,它的频域分布非常特殊,其频谱呈现出周期性衰减的形式。
在Matlab中,可以使用以下代码绘制矩形波的频谱图:```matlabFs = 100; %定义采样频率为100HzT = 1/Fs; %定义采样周期L = 1000; %定义采样点数t = (0:L-1)*T; %定义采样时间序列y = rect(t); %用自定义的rect函数生成矩形波yY = fft(y); %对y进行傅里叶变换,得到YP2 = abs(Y/L); %计算单侧频谱的幅度P1 = P2(1:L/2+1); %仅保留正半轴部分P1(2:end-1) = 2*P1(2:end-1); %将幅值乘2,除去直流分量和Nyquist频率f = Fs*(0:(L/2))/L; %定义频率向量plot(f,P1); %用plot函数将f和P1作图xlabel('f (Hz)'); ylabel('|P1(f)|');title('单侧幅度谱'); %添加横轴和纵轴标签,以及图像标题```这段代码首先定义了采样频率、采样周期、采样点数和时间序列$t$。

光波导理论与技术第一次作业题目:非对称平板波导设计*名:**学号:************指导老师:***完成日期:2014 年03 月10 日一、题目根据以下的平板光波导折射率数据:(1)作出不同波导芯层厚度h (015h m μ<<)对应的TE 模式与TM 模式的色散图;(2)给出满足单模与双模传输的波导厚度范围; (3)确定包层所需的最小厚度a 与b 的值。
二、步骤依题意知,平板波导参数为:537.11=TE n ,510.12=TE n ,444.13=TE n ;530.11=TM n ,5095.12=TM n ,444.13=TM n 。
其中321n n n 、、分别代表芯心、上包层、下包层相对于nm 1550=λ光波的折射率。
在实际应用中,平板波导的有效折射率N 必须12n N n <<才能起到导光的作用。
经过推导,非对称平板波导的色散方程为:2212322212222210arctan arctan Nn n N N n n N m N n h k --+--+=-π (TE 模) 221232232122122222212210arctan arctan N n n N n n N n n N n n m N n h k --+--+=-π (TM 模)非对称平板波导光波模式截止时对应的芯层厚度为:(TE 模)22210222123222221arctan nn k n n n n n n m h c ---+=π2221022213222arctan nn k n n n n m h c ---+=π (TM 模)非对称平板波导上下包层的最小透射深度为:222101nn k a -=(上包层)232101nn k b -= (下包层)其中a 、b 取TE 、TM 中按上述公式计算出来的结果中的最大值。
由以上分析建立脚本m 文件PlanarWaveguide.m 与函数m 文件DispersionFun.m 及MinDepthFun.m 如下:PlanarWaveguide.m 脚本文件:close all ; clear all ; clc;NTE = linspace(1.510,1.537,1000); NTM = linspace(1.5095,1.530,1000); for m = 0:3[hTE,hTM] = DispersionFun(NTE,NTM,m); plot(hTE,NTE,'r',hTM,NTM,'b'); hold on ; end ;axis([0,15,1.5090,1.538]); xlabel('h/μm'); ylabel('N');title('非对称平板波导色散曲线'); legend('TE','TM',4); grid on;gtext('m=0');gtext('m=1');gtext('m=2');gtext('m=3'); zoom on ; clc;NTE = 1.510; NTM = 1.5095;[hTEc0,hTMc0] = DispersionFun(NTE,NTM,0) [hTEc1,hTMc1] = DispersionFun(NTE,NTM,1) [hTEc2,hTMc2] = DispersionFun(NTE,NTM,2)[aMin,bMin] = MinDepthFun()DispersionFun.m函数文件:function [hTE,hTM] = DispersionFun(NTE,NTM,m)lambda = 1.55e-6;k0 = 2*pi/lambda;n1TE = 1.537;n2TE = 1.510;n3TE = 1.444;n1TM = 1.530;n2TM = 1.5095;n3TM = 1.444;hTE = 1e6*((m*pi+atan(sqrt((NTE.^2-n2TE^2)./(n1TE^2-NTE.^2)))...+atan(sqrt((NTE.^2-n3TE^2)./(n1TE^2-NTE.^2))))./(k0*sqrt(n1TE^2-N TE.^2)));hTM = 1e6*((m*pi+atan(sqrt((n1TM^2*(NTM.^2-n2TM^2))./(n2TM^2*(n1TM^2-NT M.^2))))...+atan(sqrt((n1TM^2*(NTM.^2-n3TM^2))./(n3TM^2*(n1TM^2-NTM.^2))))). /(k0*sqrt(n1TM^2-NTM.^2)));MinDepthFun.m函数文件:function [aMin,bMin] = MinDepthFun()lambda = 1.55e-6;k0 = 2*pi/lambda;n1TE = 1.537;n2TE = 1.510;n3TE = 1.444;n1TM = 1.530;n2TM = 1.5095;n3TM = 1.444;aMinTE = 1e6/(k0*sqrt((n1TE^2-n2TE^2)));aMinTM = 1e6/(k0*sqrt((n1TM^2-n2TM^2)));if(aMinTE >= aMinTM)aMin = aMinTE;elseaMin = aMinTM;end;bMinTE = 1e6/(k0*sqrt((n1TE^2-n3TE^2)));bMinTM = 1e6/(k0*sqrt((n1TM^2-n3TM^2)));if(bMinTE >= bMinTM)bMin = bMinTE;elsebMin = bMinTM;end;三、运行结果及分析实验结果共画出0~3阶TE、TM模的非对称平板波导的色散曲线,如图1所示:510151.511.5151.521.5251.531.535h/μmN平板波导色散曲线图1 非对称平板波导色散曲线同时在命令窗口得到如下运行结果: hTEc0 = 0.8555 hTMc0 = 1.0664 hTEc1 = 3.5575 hTMc1 = 4.1711 hTEc2 = 6.2595 hTMc2 = 7.2758 aMin = 0.9883 bMin = 0.4878 运行结果表示:(1)0TE 的芯层厚度范围为: 3.55758555.0<<h m ;(2)0TM 的芯层厚度范围为: 4.17111.0664<<h m μ; (3)1TE 的芯层厚度范围为: 6.25955575.3<<h m μ; (4)1TM 的芯层厚度范围为:7.27581711.4<<h m μ; (5)上包层的最小厚度为0.9883m μ; (6)下包层的最小厚度为0.4878m μ。

基于MATLAB计算软件的波导教学赵霞【摘要】将MATLAB引入到导行电磁波的计算中,借助MATLAB强大计算与可视化功能,对常见的矩形波导、圆形波导的模式分布图、场结构图、基本特点进行分析验证,有助于学生对规则金属波导的基本规律及特点的理解.【期刊名称】《实验室科学》【年(卷),期】2010(013)006【总页数】3页(P118-120)【关键词】微波技术;MATLAB;波导【作者】赵霞【作者单位】兰州交通大学自动化与电气学院,甘肃,兰州,730070【正文语种】中文【中图分类】TP319在微波技术中,规则金属波导在通信、雷达、遥感、电子对抗和测量系统中有着广泛的应用[1]。
波导的计算可以通过麦克斯韦方程和边界条件来定量描述,但是在求解的过程中会涉及大量数学计算,并且电磁场的分布是不可见的,这就导致了学生在学习过程中感觉难于理解,内容抽象[2]。
为了使学生把主要精力集中在掌握电磁场的基本概念和基本理论上,从而提高学生学习的积极性和效率,可以借助先进的计算机软件,用数值计算方法来解决较为复杂的电磁场问题,避免繁琐的手工计算[3]。
MATLAB是一个适合多学科、多种工作平台的功能强大的可视化计算软件,它有着丰富的库函数、工具箱和仿真模块,可用于科学研究和解决各种具体工程设计与计算问题[4]。
因此,用MATLAB处理电磁场数值计算时,可以利用它的偏微分方程数值求解的工具箱和编制的程序来求解未知量,并绘出电磁场的分布图[5-6]。
本文通过MATLAB和有限元法结合[7-8],对波导中的相关问题进行了分析,将复杂的计算简单化,将抽象的电磁场可视化。
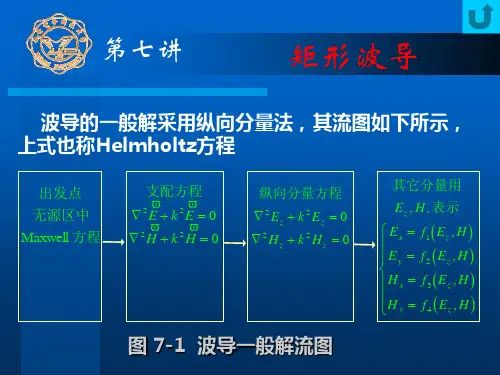
假设脊波导内为空气,且纵向均匀,采用纵向场法,波导内的场结构可以归结为求解 Helmholtz(亥姆霍兹)方程。
1 理论分析假设脊波导内为空气,且纵向均匀,采用纵向场法,波导内的场结构可以归结为求解Helmholtz(亥姆霍兹)方程。
上式中k=ω με为电磁波在无限媒质中的波数。

MATLAB有限元法求矩形波导前十个本征模的传播常数本文将介绍如何使用MATLAB有限元法求解矩形波导的本征模传播常数,并展示前十个本征模的计算结果。
这将有助于理解矩形波导的基本性质和应用。
矩形波导是一种常见的微波传输线,用于将高频信号从一个点传输到另一个点。
为了使信号的传输更加稳定和可靠,矩形波导需要满足一些特定的条件,其中之一就是要求在波导中只传输特定的波模式,即本征模。
因此,矩形波导的本征模传播常数是重要的物理量。
在MATLAB中,可以使用有限元法求解矩形波导的本征模传播常数。
下面将介绍具体的计算步骤。
首先,我们需要定义矩形波导的几何参数,包括宽度W、高度H、长度L以及介质常数εr。
在本文中,我们取W=20mm,H=10mm,L=50mm,εr=2.2。
```matlabW = 20e-3; % 宽度H = 10e-3; % 高度L = 50e-3; % 长度eps_r = 2.2; % 介质常数```其次,我们需要定义模型中的节点数和单元数。
通常情况下,节点数和单元数越多,计算结果越精确,但计算时间也会更长。
在本文中,我们取每个方向上的节点数为20,总节点数为400,总单元数为342。
```matlabnx = 20; % x方向上的节点数ny = 20; % y方向上的节点数n = nx * ny; % 节点总数n_el = 4; % 每个单元的节点数nel = (nx-1)*(ny-1); % 单元总数```然后,我们可以生成节点的坐标和单元的连接关系矩阵。
具体实现方法可以参考MATLAB官方文档中“PDE 模型和几何对象构建”一章。
```matlabmodel = createpde();%% 创建矩形波导gd = [3 4 4 0 0 2 H H 0 W W 0]';sf = 'R1';ns = char('R1');ns = ns';g = decsg(gd,sf,ns);geometryFromEdges(model,g);%% 生成节点坐标和单元连接关系[p,e,t] = initmesh(g,'Hmax',0.005); % Hmax为最大单元边长```节点坐标和单元连接关系矩阵的生成将自动对模型进行离散化。

MATLAB有限元法求矩形波导前十个本征模的传播常数介绍矩形波导是一种常见的波导结构,广泛应用于微波和光波器件中。
它的传播特性可以通过有限元法进行模拟和分析。
本文将介绍如何使用MATLAB进行矩形波导的有限元法求解,并计算前十个本征模的传播常数。
有限元法基本原理有限元法是一种常见的数值分析方法,用于求解偏微分方程。
它将求解域分割为多个离散的单元,并通过在单元内插值来逼近解。
在矩形波导的有限元法中,我们将波导截面分割为多个单元,通过在这些单元上插值电场和磁场来近似求解波导的模式。
有限元法模拟矩形波导有限元法模拟矩形波导的前提是先将波导截面分割为多个单元。
在矩形波导中,我们可以使用矩形节点阵列来表示截面的离散点。
例如,可以通过定义矩阵X和Y来表示波导截面上的坐标点。
x = linspace(0, a, Nx);y = linspace(0, b, Ny);[X, Y] = meshgrid(x, y);其中,a和b分别表示矩形波导的宽度和高度,Nx和Ny是我们在x和y方向上的离散点数。
接下来,我们可以使用插值方法在每个单元上近似波导内的电场和磁场分布。
在此,我们使用双线性插值方法。
我们假设波导中的电场和磁场可以由下面的插值方程表示:E = F11 * f11 + F12 * f12 + F21 * f21 + F22 * f22;H = G11 * g11 + G12 * g12 + G21 * g21 + G22 * g22;其中,f11、f12、f21和f22分别表示四个节点上的电场值,g11、g12、g21和g22分别表示四个节点上的磁场值。
F11、F12、F21、F22和G11、G12、G21、G22是插值系数。
利用这些插值方程,我们可以得到波导内的电磁场分布,并通过调整插值节点和单元数目来获得更准确的结果。
求解传播常数通过模拟矩形波导中的电磁场分布,我们可以计算出该结构的传播常数。
传播常数表示电磁波在波导中传播的速率和损耗情况。

光波导理论与技术第二次作业题目:条形波导设计*名:**学号:************指导老师:***完成日期:2014 年03 月19 日一、题目根据条形光波导折射率数据,条形波导结构如图1所示,分别针对宽高比d a :为1:1与1:2两种情形,设计:(1)满足单模与双模传输的波导尺寸范围;(需要给出色散曲线) (2)针对两种情况,选取你认为最佳的波导尺寸,计算对应的模折射率。
(计算时假设上、下包层均很厚)图1 条形波导横截面示意图二、步骤依题意知,条形波导参数为:5370.11=TE n ,5100.12=TE n ,444.13=TE n ;5360.11=TM n ,5095.12=TM n ,444.13=TM n 。
其中321n n n 、、分别代表芯心、上包层、下包层相对于nm 1550=λ光波的折射率。
本设计采用有效折射率法作条形波导的归一化色散曲线,条形波导的横截面区域分割情况如图2所示:图2 条形波导横截面分割图对于xmn E 模式,x E 满足如下波动方程:[]0),(22202222=-+∂∂+∂∂eff x x n y x n k yE x E 由于导波模式在x 与y 方向上是非相干的,采用分离变量法后再引入)(220x N k 得到如下两个独立的波动方程:0)()](),([)(222022=-+∂∂y Y x N y x n k yy Y 0)(])([)(222022=-+∂∂x X n x N k xx X eff 可以将条形波导等效成y 方向和x 方向受限的平板波导,先求y 方向受限平板波导的TE 模式,求得x N 后将其作为x 方向受限的平板波导的芯层折射率并求其TM 模式,得到的有效折射率eff n 就是整个条形波导的有效折射率。
y 方向受限平板波导的TE 模式的色散方程为:2212422212222210arctan arctan xx x x xN n n N N n n N n N n d k --+--+=-π (...2,1,0=n ) 其中1n 、2n 、4n 都是TE 模式的有效折射率从而x 方向受限平板波导的TM 模式的色散方程为:⎪⎪⎭⎫ ⎝⎛--+⎪⎪⎭⎫ ⎝⎛--+=-2225225222232232220arctan arctan eff x eff xeffx eff xeffx n N n n n N n N n n n N m nN a k π(...2,1,0=m ) 其中3n 、5n 都是TM 模式的有效折射率。

设计工作1(1) T E 模式和TM 模式的色散方程用有效折射率分别表示为:0k m π=++----------(TE )0k m π=++-------(TM ) 我们取m=0,1,2,3分别求出有效折射率N 与波导芯厚度h 的关系。
用Matlab 实现,程序如下:%不同波导芯厚度h 对应的TE 模式也TM 模式色散图程序k0=2*pi/1.55;for m=0:1:3n1=1.537; %TE 模式下的折射率分布 n2=1.444;n3=1.51;N1=1.510:0.0001:1.537; %TE 模式下有效折射率的范围 %TE 模式下波导芯厚度h_te=(m*pi.*ones()+atan(((N1.^2-n2.^2)./(n1.^2-N1.^2)).^0.5)+atan(((N1.^2-n3.^2)./(n1.^2-N1.^2)).^0.5))./(k0.*(n1.^2-N1.^2).^0.5);n1=1.530; %TM 模式下的折射率分布 n2=1.444;n3=1.5095;N2=1.5095:0.0001:1.530; %TM 模式下有效折射率的范围%TM模式下波导芯厚度h_tm=(m*pi.*ones()+atan((((N2.^2-n2.^2)./(n1.^2-N2.^2)).^0.5).*n1.^2. /n2.^2)+atan((((N2.^2-n3.^2)./(n1.^2-N2.^2)).^0.5).*n1.^2./n3.^2))./(k0. *(n1.^2-N2.^2).^0.5);title('色散图')plot(h_te,N1,'-b',h_tm,N2,'-r')axis([0,15,1.509,1.537])legend('TE','TM','Location','Northwest')xlabel('h(um)','fontsize',10)ylabel('N','fontsize',10)hold ongrid ongrid minorend色散图为:(2)当波导厚度薄到仅基模能传播的时候,该波导称为单模波导。

色散曲线简介色散曲线是描述光在不同波长下折射率变化的曲线。
在光学领域中,光的折射是由于光通过了不同介质引起的,而不同波长的光在介质中的传播速度以及折射程度也会有所不同,这就形成了色散现象。
色散曲线可以用来分析不同波长下光的折射情况,对于光学设计和实验研究有着重要的意义。
色散的定义色散是光在折射过程中,由于介质折射率对光波长的依赖性而产生的现象。
当入射的光波呈现出不同波长的成分时,不同波长的光在介质中的折射情况不同,导致出射光的波长分离,进而产生折射角的变化。
形成色散曲线的原因色散曲线的形成是由于光在介质中传播速度与波长相关的性质。
由于折射率是光在介质中传播速度的倒数,所以不同波长的光在介质中的折射率也会不同。
光的速度是光在真空中的速度除以介质的折射率。
而根据光的频率与波长的关系,我们知道光波长越短,频率越高。
所以,在光通过介质时,波长较短的光速度会比波长较长的光速度更快,而波长较短的光折射率会比波长较长的光折射率更大,因此由此产生了色散现象。
色散曲线的分类色散曲线根据折射率与波长的关系可以分为以下几种类型:正常色散正常色散是指随着波长减小,折射率也随之减小的情况。
在正常色散情况下,折射角随着入射光波长的减小而变小,即波长越短,折射角越小。
负色散负色散是指随着波长减小,折射率也随之增加的情况。
在负色散情况下,折射角随着入射光波长的减小而增加,即波长越短,折射角越大。
零色散零色散是指在特定的波长下,折射率不随波长而变化。
在零色散情况下,折射角与入射光波长无关。
色散曲线的应用色散曲线的研究对光学设计和实验研究有着重要的意义。
色散的存在和性质决定了许多光学器件的功能和性能。
棱镜棱镜是一种常用的光学器件,它能将不同波长的光分离出来,实现光的分光。
根据色散曲线的性质,波长越短的光在棱镜中的折射角会更大,从而使得不同波长的光发生分离。
光纤光纤是一种能够将光信号进行传输的光学器件。
由于不同波长的光在光纤中的传播速度不同,所以光在光纤中的传播速度也会发生变化,这就导致了信号的色散现象。

MATLAB矩形波简介矩形波是一种周期性的信号,其波形由一系列等宽的方波组成。
在MATLAB中,我们可以使用各种方法来生成和处理矩形波信号。
本文将介绍如何使用MATLAB生成矩形波信号、修改其参数以及进行频谱分析。
生成矩形波信号在MATLAB中,我们可以使用square函数来生成矩形波信号。
该函数的基本语法如下:y = square(t, duty)其中,t是时间变量,表示要生成的信号的时间范围;duty是占空比,表示方波高电平持续时间与周期的比例。
下面是一个简单的示例代码,演示了如何生成一个周期为2秒、占空比为0.5的矩形波信号:t = 0:0.01:10; % 时间范围从0到10秒,步长为0.01秒duty = 0.5; % 占空比为0.5y = square(t, duty); % 生成矩形波信号plot(t, y); % 绘制波形图xlabel('Time (s)'); % X轴标签ylabel('Amplitude'); % Y轴标签title('Square Wave'); % 图片标题grid on; % 显示网格运行以上代码,将会生成一个周期为2秒、占空比为0.5的矩形波信号的波形图。
修改矩形波参数除了基本的时间范围和占空比之外,我们还可以通过修改其他参数来改变矩形波信号的特性。
频率和周期矩形波信号的频率是指单位时间内周期的个数,频率的倒数即为周期。
在MATLAB 中,我们可以通过修改时间变量的步长来改变频率和周期。
例如,如果我们将上面示例代码中的步长由0.01秒改为0.1秒,则生成的矩形波信号将具有更低的频率和更长的周期。
占空比矩形波信号的占空比是指方波高电平持续时间与周期之间的比例。
在上面示例代码中,我们将占空比设置为0.5,即高电平持续时间等于低电平持续时间。
如果我们将占空比设置为0.2,则方波高电平持续时间仅为低电平持续时间的五分之一。
专题研究:矩形波导TE 模波各模式的MATLAB 实现信息与通信工程 徐锋南 3071102319ABSTRACT :本文主要依据电磁场与电磁波课本推导的矩形波导TE 模波各模式的分布公式,利用MATLAB 强大的图形显示和计算功能,从矩形波导的各个平面对TE 模波的各模式进行了静态分析和动态分析,旨在加强同学们对矩形波导的理解。
一、 理论预备1、根据《电磁场与电磁波》(第二版),将矩形波导的推导公式展示如下:其中主要参数的说明:(以TEmn 模为例) m : x 方向驻波的半波个数 n : y 方向驻波的半波个数 a : 矩形波导x 向的物理长度 b : 矩形波导y 向的物理长度mn A : 常数Kz : z 向的传播常数 w : 电磁波的频率 t :传播时间∑−=nm z k t j mnx z e y b n x a m b n A E ,)( sin cos 'ωπππ∑−−=nm z k t j mny z e y bn x a m a m A E ,)( cos sin 'ωπππ0'=z E ∑−=nm z k t j z mnx z e y b n x a m am k A H ,)( cos sin 'ωπππωμ∑−=nm z k t j z mny z e y b n x a m bn k A H ,)( sin cos 'ωπππωμ∑−⎥⎦⎤⎢⎣⎡+−=nm z k t j mn z ze y b n x a m a m b n jA H ,)(22222 cos cos 'ωππωμπ2、主模TE10模)(10sinz k t j y z e x aaA E −−=ωππ)(10sin z k t j z x z e x aa k A H −=ωππωμ )(2210 cos 1z k t j z z e x aa jA H −−=ωππωμ 0===y z x H E E二、主要MATLAB 函数简介1、meshgrid『用法』:[X,Y] = MESHGRID(x,y)『作用』:将x ,y 转换成能画3 D 的数据。
BPM波导matlab,⽤Matlab画平板波导⾊散图详解.doc根据以下的平板光波导在波长为1550 nm时的折射率数据,(1)作出不同波导芯厚度h(0(2)给出满⾜单模与双模传输的波导厚度范围;(3)确定包层所需的最⼩厚度a与b的值。
解答:(1)⾊散图如下:由图可得出该波导结构在1550nm波长处⼏点规律 :1、当波导芯厚度和模式相同时,TM模的等效折射率⼤于TE模的等效折射率;2、当波导芯厚度相同时,⾼阶模的等效折射率都⽐低阶的⼤很多;3、当模式⼀定时,TE模和TM模的等效折射率都随芯层厚度增⼤⽽增⼤,最后趋于稳定。
(2)某个模式(即导模)能在波导结构稳定传输,就意着它在芯层传输的 等效折射率⼤于周围介质层的折射率,否者不能在芯层稳定传输。
单模传输,那么只能允许基模传输,所以由⾊散图可知芯层厚度h应该⼤于1.0241μm,但由允许⼀阶模传输,那么芯层厚度h应该⼩于3.8554μm,所以该波导单模传输的芯层厚度范围为:1.0241μm < h < 3.8554μm。
同理可分析出双模传输的芯层厚度范围为:3.8554μm < h < 6.4458μm。
(3)由公式,,,可得, 。
单模传输时,N取临界最⼤值1.528。
则通过matlab计算可得a > 1 / p = 1.0853μm;b > 1 / q = 0.4949μm。
双模传输时,N取临界最⼤值1.5328。
则通过matlab计算可得a > 1 / p = 0.9577μm;b > 1 / q = 0.4809μm。
(4)波长放⼤⼗倍的分析由上图可知,忽略⾊散时,波长放⼤⼗倍后,为了是光波在波导中稳定传输,所需的最⼩芯层厚度变⼤了很多。
% clear all% clc;% % 画平板光波导波导层厚度h关于有效折射率N的⾊散图% syms y x% n3 = 1.4444;% lambda = 15.5;% k = 2 * pi / lambda;% figure;% for m = 0:3 %做0到3阶模的循环% %画TE模的⾊散图% n1 = 1.5350;% n2 = 1.5105;% h = ezplot(m*pi + atan(sqrt((y^2*k^2 - n2^2*k^2)/( n1^2*k^2 - y^2*k^2 ))) + atan(sqrt((y^2*k^2 - n3^2*k^2)/( n1^2*k^2 -y^2*k^2 ))) - sqrt(n1^2*k^2 - y^2*k^2 )*x,[0,45,1.44,1.54]);% set(h,'color','r','linewidth',1.2);% hold on;% %画TM模的⾊散图% n1 = 1.5365;% n2 = 1.5110;% h = ezplot(m*pi + atan((n1^2/n2^2)*sqrt((y^2*k^2 - n2^2*k^2)/( n1^2*k^2 - y^2*k^2 ))) +atan((n1^2/n3^2)*sqrt((y^2*k^2 - n3^2*k^2)/( n1^2*k^2 - y^2*k^2 ))) - sqrt(n1^2*k^2 - y^2*k^2 )*x,[0,45,1.44,1.54]);% set(h,'color','g','linewidth',1.2);% hold on;% end% %画N = 1.5105,以便判断TE模的最⼩波导厚度% y = 1.5105;% x = 0:0.1:45;% plot(x,y,'-');% hold off;%clear allclc;n3 = 1.4444;lambda = 1.55;k = 2 * pi / lambda;for m = 0:3n1 = 1.5350;n2 = 1.5105;N_TE = 1.5:0.0000001:1.5365;h_TE = (m*pi.*ones + atan(sqrt((N_TE.^2 - n2^2)./(n1^2 - N_TE.^2))) + atan(sqrt((N_TE.^2 - n3^2)./(n1^2 - N_TE.^2))))./...(sqrt(n1^2*k^2 - N_TE.^2*k^2) );n1 = 1.5365;n2 = 1.5110;N_TM = 1.5:0.0000001:1.5365;h_TM = (m*pi.*one。
光波导理论与技术第二次作业
题目:条形波导设计
姓名:王燕
学号:201321010126
指导老师:陈开鑫
完成日期:2014 年03 月19 日
一、题目
根据条形光波导折射率数据 ,条形波导结构如图1所示 ,分别针对宽高比
d a :为1:1与1:2两种情形 ,设计:
(1)满足单模与双模传输的波导尺寸范围;(需要给出色散曲线) (2)针对两种情况 ,选取你认为最佳的波导尺寸 ,计算对应的模折射率。
(计算时假设上、下包层均很厚)
图1 条形波导横截面示意图
二、步骤
依题意知 ,条形波导参数为:5370.11=TE n ,5100.12=TE n ,444.13=TE n ;
5360.11=TM n ,5095.12=TM n ,444.13=TM n 。
其中321n n n 、、分别代表芯心、上
包层、下包层相对于nm 1550=λ光波的折射率。
本设计采用有效折射率法作条形波导的归一化色散曲线 ,条形波导的横截面区域分割情况如图2所示:
图2 条形波导横截面分割图
对于x
mn E 模式 ,x E 满足如下波动方程:
[]
0),(2
2202
222=-+∂∂+∂∂eff x x n y x n k y
E x E 由于导波模式在x 与y 方向上是非相干的 ,采用分离变量法后再引入)(220x N k 得到如下两个独立的波动方程:
0)()](),([)(2
2202
2=-+∂∂y Y x N y x n k y
y Y 0)(])([)(2
2202
2=-+∂∂x X n x N k x
x X eff 可以将条形波导等效成y 方向和x 方向受限的平板波导 ,先求y 方向受限平板波导的TE 模式 ,求得x N 后将其作为x 方向受限的平板波导的芯层折射率并求其
TM 模式 ,得到的有效折射率eff n 就是整个条形波导的有效折射率。
y 方向受限平板波导的TE 模式的色散方程为:
2
2124
222122222
1
0arctan arctan x
x x x x
N n n N N n n N n N n d k --+--+=-π (...2,1,0=n ) 其中1n 、2n 、4n 都是TE 模式的有效折射率从而x 方向受限平板波导的TM 模式的色散方程为:
⎪⎪⎭
⎫ ⎝⎛--+⎪⎪⎭⎫ ⎝⎛--+=-2225
22522223
22
32
220arctan arctan eff x eff x
eff
x eff x
eff
x n N n n n N n N n n n N m n
N a k π(...2,1,0=m ) 其中3n 、5n 都是TM 模式的有效折射率。
对于y
mn E 模式 ,y E 满足如下波动方程:
[]
0),(2
2202
22
2=-+∂∂+
∂∂eff y y n y x n k y
E x
E
由于导波模式在x 与y 方向上是非相干的 ,采用分离变量法后再引入)(220x N k 得到如下两个独立的波动方程:
0)()](),([)(2
2202
2=-+∂∂y Y x N y x n k y
y Y 0)(])([)(2
2202
2=-+∂∂x X n x N k x
x X eff 可以将条形波导等效成y 方向和x 方向受限的平板波导 ,先求y 方向受限平板波导的TM 模式 ,求得x N 后将其作为x 方向受限的平板波导的芯层折射率并求其
TE 模式 ,得到的有效折射率eff n 就是整个条形波导的有效折射率。
y 方向受限平板波导的TM 模式的色散方程为:
⎪⎪⎭
⎫
⎝
⎛--+⎪⎪⎭⎫ ⎝
⎛--+=-2
212
4
224
21
2
2122
22
22
1221
0arctan arctan x
x x
x x
N n n N n n N n n N n n n N n d k π(...2,1,0=n ) 其中1n 、2n 、4n 都是TM 模式的有效折射率从而x 方向受限平板波导的TE 模式的色散方程为:
2225
22223
2220arctan
arctan
eff
x eff eff
x eff eff
x
n
N n n n
N n n m n
N a k --+--+=-π (...2,1,0=m )
其中3n 、5n 都是TE 模式的有效折射率。
由以上分析建立脚本m 文件BarWaveguide.m 与四个函数m 文件yTE_DispersionFun.m 、yTM_DispersionFun.m 、xTE_DispersionFun.m 、xTM_DispersionFun.m 如下:
BarWaveguide.m 脚本文件:
close all ; clear all ; clc;
global V b;
% a:d = 1:1
figure(1);
% x方向偏振
NTEx = linspace(1.5100, 1.5370, 2000);
for n = 0:1
dTE = yTE_DispersionFun(NTEx, n);
for m = 0:1
k = 1;
for i = 1:2000
if(NTEx(i) <= 1.5360)
NTMe = linspace(1.5100, NTEx(i), 4000);
aTM = xTM_DispersionFun(NTMe, NTEx(i), m);
for j = 1:4000
if(abs(aTM(j) - dTE(i)) < 2e-2) V(k) = 2*dTE(i)*sqrt(1.5360^2 -1.5100^2);
b(k) = (NTMe(j)^2 - 1.5100^2)/(1.5360^2 -1.5100^2);
k = k+1;
end;
end;
end;
end;
plot(V, b,'r');
hold on;
pause;
clear V b;
end;
end;
% y方向偏振
NTMx = linspace(1.5095, 1.5360, 2000);
for n = 0:1
dTM = yTM_DispersionFun(NTMx, n);
for m = 0:1
k=1;
for i = 1:2000
NTEe = linspace(1.5100, NTMx(i), 4000);
aTE = xTE_DispersionFun(NTEe, NTMx(i), m);
for j = 1:4000
if(abs(aTE(j) - dTM(i)) < 2e-3)
V(k) = 2*dTM(i)*sqrt(1.5360^2 - 1.5100^2);
b(k) = (NTEe(j)^2 - 1.5100^2)/(1.5360^2 - 1.5100^2);
k = k+1;
end;
end;
end;
plot(V,b,'b');
hold on;
pause;
clear V b;
end;
end;
axis([0, 5, 0, 1]);
xlabel('V');
ylabel('b');
title('归一化色散曲线 a:d = 1:1');
gtext('E11');gtext('E12');gtext('E21');gtext('E22');
zoom on;
% a:d = 2:1
figure(2);
% x方向偏振
NTEx = linspace(1.5100, 1.5370, 2000);
for n = 0:1
dTE = yTE_DispersionFun(NTEx, n);
for m = 0:1
k = 1;
for i = 1:2000
if( NTEx(i) <= 1.5360)
NTMe = linspace(1.5100, NTEx(i), 4000);
aTM = xTM_DispersionFun(NTMe, NTEx(i), m);
for j = 1:4000。