下载文档原格式
5.6 利用开环频率特性分析系统的性能在频域中对系统进行分析、设计时，通常是以频域指标作为依据的，但是不如时域指标来得直接、准确。
因此，须进一步探讨频域指标与时域指标之间的关系。
考虑到对数频率特性在控制工程中应用的广泛性，本节将以Bode 图为基点，首先讨论开环对数幅频特性)(ωL 的形状与性能指标的关系，然后根据频域指标与时域指标的关系估算出系统的时域响应性能。
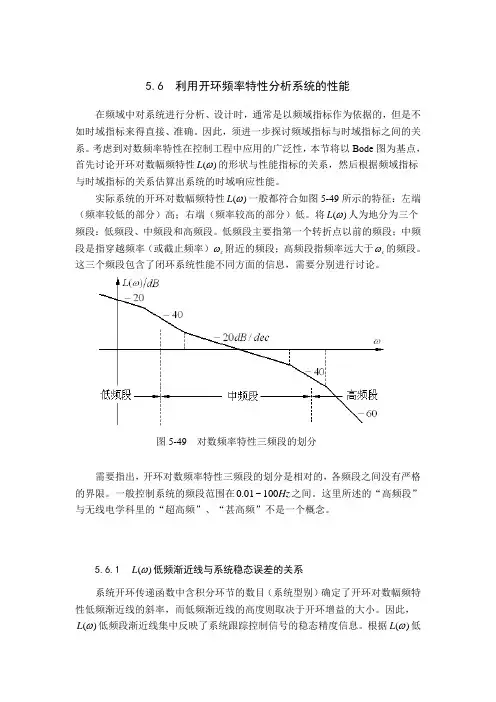
实际系统的开环对数幅频特性)(ωL 一般都符合如图5-49所示的特征：左端（频率较低的部分）高；右端（频率较高的部分）低。
将)(ωL 人为地分为三个频段：低频段、中频段和高频段。
低频段主要指第一个转折点以前的频段；中频段是指穿越频率（或截止频率）c ω附近的频段；高频段指频率远大于c ω的频段。
这三个频段包含了闭环系统性能不同方面的信息，需要分别进行讨论。
需要指出，开环对数频率特性三频段的划分是相对的，各频段之间没有严格的界限。
一般控制系统的频段范围在Hz 100~01.0之间。
这里所述的“高频段”与无线电学科里的“超高频”、“甚高频”不是一个概念。
5.6.1 )(ωL 低频渐近线与系统稳态误差的关系系统开环传递函数中含积分环节的数目（系统型别）确定了开环对数幅频特性低频渐近线的斜率，而低频渐近线的高度则取决于开环增益的大小。
因此，)(ωL 低频段渐近线集中反映了系统跟踪控制信号的稳态精度信息。
根据)(ωL 低图5-49 对数频率特性三频段的划分频段可以确定系统型别υ和开环增益K ，利用第3章中介绍的静态误差系数法可以确定系统在给定输入下的稳态误差。
5.6.2 )(ωL 中频段特性与系统动态性能的关系开环对数幅频特性的中频段是指穿越（或截止）频率c ω附近的频段。
设开环部分纯粹由积分环节构成，图5-50（a ）所示的对数幅频特性对应一个积分环节，斜率为dec dB /20-，相角 90)(-=ωϕ，因而相角裕度 90=γ；图5-50（b ）的对数幅频特性对应两个积分环节，斜率为dec dB /40-，相角 180)(-=ωϕ，因而相角裕度 0=γ。
主要内容系统闭环频率特性通过频率特性曲线分析稳态性能指标频域动态性能指标频率域特性指标与时域瞬态指标的关系2)()(1)()()(1s H s G s H s G s H +⋅=4环幅频特性。
闭环幅频特性曲线闭环对数幅频曲线二、由闭环频率特性分析系统的时域响应频率特性分析法比时域性能分析简便，且有成熟的图解法可供使用，但频率特性分析是一种概略性的间接方法，在要求系统性能指标直接而具体时，还需从时域响应面进行讨论。
在已知闭环系统稳定的条件下，可根据系统的闭环幅频特性曲线，对系统的动态过程进行定性分析与定量估算。
51、通常的闭环频域有以下几个指标：V零频幅值：ω=0时闭环幅频特性的数值(反映系统静差（误差）)V谐振频率ωr：闭环系统频率特性出现谐振峰值时的频率值V谐振峰值M r：系统闭环频率特性幅值的最大值，反映系统的平稳性，并非所有闭环频率特性的中频段有谐振峰值，若出现了谐振峰值，表明系统的阻尼比较小615M r、σ与ζ的关系曲线当相角裕量γ为30o ~60o 时，对应二阶系统的阻尼比ζ为0.3~0.6在ζ≤0.707时，二阶系统的相角裕量γ与阻尼比ζ之间的关系近似为：ζ=0.01γV谐振频率ωr表征系统瞬态响应的速度。
ωr值越大,响应时间越快。
对于弱阻尼系统(ζ较小),谐振频率ωr与阶跃响应的阻尼振荡频率ωd接近。
V截止频率（带宽频率）ωb当系统闭环幅频特性的幅值M(ω)降到零频率幅值的0.707(或零分贝值以下3dB)时，对应的频率ωb称为截止频率。
0～ωb的频率范围称为带宽它反映系统的快速性和低通滤波特性。
V剪切率ωc幅值=1时的频率ωc，称为剪切率，它既反映系统的相角裕度(相角裕度大,剪切率应较平缓),又表征系统从噪声中辨别信号的能力(剪切率平缓,带宽ωb大,对高频噪声的抑制不利)。
17应注意，剪切频率ωc处斜率平缓(如以-20dB/dec过0dB线)时，系统相角裕量大；而斜率陡峭时，说明具有负相角的环节集图5 剪切率中叠加于此，带来大的负相角,如图5所示，则易造成系统不稳定。
