v: 包含主轴的对称面。 分为:
h: 垂直于主轴的对称面。 d: 包含主轴且平分垂直于主轴的两个相 邻C2轴夹角的平面。
C2 [Re2Cl8]2σd
试找出分子中的镜面
反映的矩阵表示:
1 0 0 ˆ xy 0 1 0 0 0 1 1 0 0 ˆ yz 0 1 0 0 0 1 1 0 0 ˆ zx 0 1 0 0 0 1
1.封闭性 若A G, B G, 则必有AB C, C G
C2v{C2z , xz , yz , E}
[ x, y , z ] [ x, y , z ] [ x, y , z ] [ x, y , z ] [ x, y , z ] C
z 2 xz yz
3
ˆ1 C3 ˆ C1
vc
va
ˆ1 C3 ˆ C2
3 a v b v c v
ˆ ˆ va ˆ ˆ vb ˆ ˆ vc
ˆ C ˆ E b ˆv ˆc v ˆ va
3 2 3
ˆ2 C3 ˆ C2
ˆ E ˆ1 C3 c ˆv ˆ va ˆb v
3
ˆ va c ˆv ˆb v
k
,
其中
旋转轴 1 作用在空间点
上,可得到另一个点
1
C2(z), C2(x), C2(y)
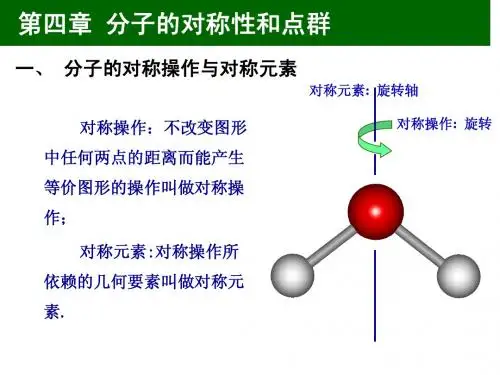
2、镜面与反映操作
分子中若存在一个平面,将
分子两半部互相反映而能使分子
复原,则该平面就是镜面σ,这 种操作就是反映.
对称面的正逆操作相同,即:
ˆ
ˆ
E ˆ ˆ ˆ
按与主轴的关系:
一个分子具有的全部对称元素构成一个完整的 对称元素系,和该对称元素系对应的全部对称操作 形成一个对称操作群,群是按照一定规律相互联系 着的一些元(又称元素)的集合,这些元可以是操作、 数字、 矩阵或算符等。在本章中群的元均指对称操 作或对称操作的矩阵。 连续做两个对称操作即和这两个元的乘法对应。 若对称操作A,B,C,…的集合G={A,B,C,…}同时满足 下列四个条件,这时G形成一个群。