图论05-哈密尔顿图
- 格式:ppt
- 大小:690.50 KB
- 文档页数:29



离散数学-图论-哈密顿图及其应⽤哈密顿图⼀、定义概念1.哈密顿通路设G=<V,E>为⼀图(⽆向图或有向图).G中经过每个顶点⼀次且仅⼀次的通路称作哈密顿通路2.哈密顿回路G中经过每个顶点⼀次且仅⼀次的回路(通路基础上+回到起始点)称作哈密顿回路3.哈密顿图若G中存在哈密顿回路,则称它是哈密顿图4.定义详解:(1)存在哈密顿通路(回路)的图⼀定是连通图;(2)哈密顿通路是初级通路,哈密顿回路是初级回路;(3)若G中存在哈密顿回路,则它⼀定存在哈密顿通路,反之不真(看课本的话,是必要条件,⽽不是充分条件,故不可反推!)(4)只有哈密顿通路,⽆哈密顿回路的图不叫哈密顿图;即,哈密顿图是回路⼆、判定定理注意:⽬前还没有找到哈密顿图的简单的充要条件(1)设⽆向图G=<V,E>为哈密顿图,V1是V的任意真⼦集,则(注:n阶xx图指的是n个顶点,不要迷!)p(G-V1)<=|V1|其中,p(G-V1)为G中删除V1后的所得图的连通分⽀数⽬,|V1|为V1集合中包含的顶点个数。
【哈密顿图存在的必要条件】推论:有割点的图⼀定不是哈密顿图设v是图中的割点,则p(G-v)>=2,由上述定理知G不是哈密顿图(2)设G是n(n>=3)阶⽆向简单图,若对于G中的每⼀对不相邻的顶点u,v,均有d(u)+d(v)>=n-1则G中存在哈密顿通路。
⼜若d(u)+d(v)>=n则G中存在哈密顿回路,即G为哈密顿图。
【哈密顿图存在的充分条件,不是必要条件】其中d(u),d(v)分别代表顶点u,v的度数。
推论:设G是n(n>=3)阶⽆向简单图,若G的最⼩度>=n/2,则G是哈密顿图。
由推论知,对于完全图Kn,当n>=3时,是哈密顿图,完全⼆部图Kr,s当r==s>=2时是哈密顿图。
(3)在n(n>=2)阶有向图D=<V,E>中,如果略去所有有向边的⽅向,所得⽆向图中含⽣成⼦图Kn,则D中存在哈密顿通路。
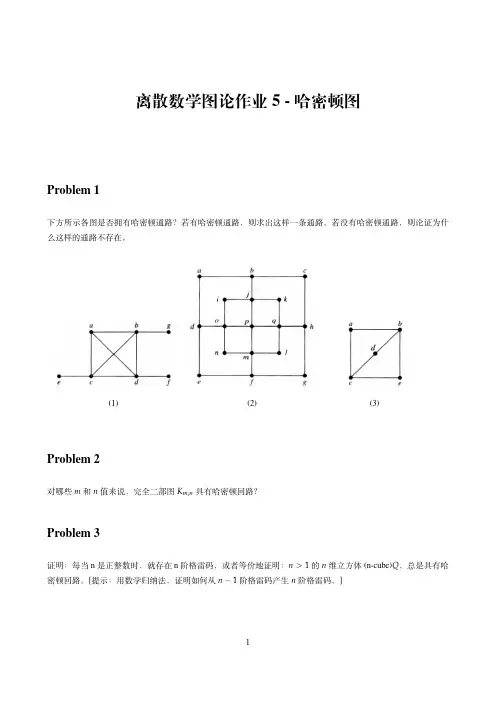
离散数学图论作业5-哈密顿图
Problem1
下方所示各图是否拥有哈密顿通路?若有哈密顿通路,则求出这样一条通路。
若没有哈密顿通路,则论证为什么这样的通路不存在。
(1)(2)(3)
Problem2
对哪些m和n值来说,完全二部图K m,n具有哈密顿回路?
Problem3
证明:每当n是正整数时,就存在n阶格雷码,或者等价地证明:n>1的n维立方体(n-cube)Q,总是具有哈密顿回路。
[提示:用数学归纳法,证明如何从n−1阶格雷码产生n阶格雷码。
]
证明:下图所示的彼得森图没有哈密顿回路,但删除任意顶点v和所有与v关联的边,所获得的子图都有哈密顿回路。
Problem5
若简单图G满足V(G)≥3且δ(G)≥V(G)−1
,证明或反驳:
2
a)G一定存在哈密顿回路。
b)G一定存在哈密顿通路。
Problem6
底图是完全图的有向图称为竞赛图,试证明:
a)竞赛图一定含有哈密顿通路。
b)竞赛图含有哈密顿回路的充分必要条件是强连通。
Problem7
考虑在15天安排15门课程的考试(每天考1门课),使得同一位老师所任的任意两门课程考试不排在接连的两天中,试证明如果没有老师担任多于8门课程,则符合上述要求的考试安排总是可能的。
考虑M×N的网格,以其中的方格作为点集,任意两个点之间有边当且仅当对应的两个方格相邻,构成图G。
a)当N是偶数且M>1时,给出一种哈密顿回路的构造方法。
b)当N和M都是大于1的奇数时,证明此时G没有哈密顿回路。


定义4.3.1 经过图G 的每个顶点恰一次的路称为G 的Hamilton 路,简称为H 路。
经过图G 的每个顶点恰一次的圈称为G 的Hamilton 圈,简称为H 圈。
具有Hamilton 圈的图称为Hamilton 图,简称为H 图。
Hamilton 图的研究起源于一种十二面体上的游戏。
1857 年,爱尔兰著名数学家William Rowan Hamilton 爵士(他也是第一个给出复数的代数描述的人)制作了一种玩具,它是一个木制的正十二面体,在正十二面体的每个顶点上有一个木栓,并标有世界著名城市的名字。
游戏者用一条细线从一个顶点出发,设法沿着十二面体的棱找出一条路,通过每个城市恰好一次,最后回到出发点。
这个游戏当时称为Icosian 游戏,也称为周游世界游戏。
将正十二面体从一个面剖开并铺展到平面上得到的图形如下图所示,称为十二面体图。
周游世界游戏用图论术语来说就是判断十二面体图是否Hamilton 图,并设法找出其Hamilton 圈。
其中一条Hamilton 圈如图中粗边所示。
十二面体图是H 图判断一个图是否Hamilton 图与判断一个图是否Euler 图似乎很相似,然而二者却有本质的不同。
目前为止尚没有找到判别一个图是否是Hamilton 图的有效充要条件。
这是图论和计算机科学中未解决的重要难题之一。
本节给出一些经典的充分条件和必要条件。
一、必要条件定理4.3.1 设G 是二部图,若G 是H 图,则G 必有偶数个顶点。
证明:设G = (X, Y ) ,由于G 的边全在X 和Y 之间,因此如果G 有Hamilton 圈C,则G的所有顶点全在C 上,且必定是X 的点和Y 的点交替在C 上出现,因此G 必有偶数个顶点。
证毕。
这个定理给出了一个二部图不是Hamilton 图的简单判断条件:如果一个二部图有奇数个顶点,则它必定不是Hamilton 图。
例如,下列Herschel 图是二部图,但有奇数个顶点,故不是H 图。


3.3.2 哈密尔顿图哈密尔顿(W.Hamilton)于1859 Array年提出了确定一个图是否有一条生成路或生成圈的问题。
这个问题是从哈密尔顿发明的一个数学游戏引出的。
1859年哈密尔顿发明了一种游戏,并作为一个玩具以25个金币卖给了一个玩具商。
这个玩具是用12个正五边形的面做成的一个正12面体,这个12面体共20个顶点,并以世界上20个著名城市名命名,要求游戏者沿着这个12面体的棱,走遍每个城市一次且仅一次,最后回到出发点。
他把这个游戏称之为“周游世界”游戏。
这个问题归结为求上图的一个哈密顿圈。
按图中的编号顺序走,显然会成功。
定义1 设G是无向图,则称经过每个结点一次且仅一次的通路为哈密尔顿通路。
如果哈密尔顿通路是回路,则称其为哈密尔顿回路。
具有哈密尔顿回路的G,称为哈密尔顿图。
确定一个图是否为哈密顿图的问题称为哈密顿回路问题。
由定义可知:(1)具有哈密尔顿通路的图是连通的;(2)哈密尔顿通路是初级通路;(3)哈密尔顿回路是初级回路。
对于有向图可类似定义。
定义2 设D是有向图,则称经过每个结点一次且仅一次的有向通路为有向哈密尔顿通路。
如果有向哈密尔顿通路是有向回路,则称其为有向哈密尔顿回路。
具有有向哈密尔顿回路的D,称为有向哈密尔顿图。
由有向哈密尔顿图的定义可知:(1)具有有向哈密尔顿通路的图是单向连通的;(2)有向哈密尔顿通路是初级有向通路;(3)有向哈密尔顿回路是初级有向回路。
例1 下面的图形中,哪个没有哈密尔顿通路?哪个有哈密尔顿通路但无哈密尔顿回路?哪个是哈密尔顿图?a a a(1) (2) (3)解 (1)中有哈密尔顿回路,例如 abcdea ,(1)是哈密尔顿图; (2)中无哈密尔顿通路;(3)中有哈密尔顿通路,例如 badce ,无哈密尔顿回路,不是哈密尔顿图。
例2 判断下面所示的有向图中,哪个没有有向哈密尔顿通路?哪个有有向哈密尔顿通路但无有向哈密尔顿回路?哪个是有向哈密尔顿图?3 3v 3v 5v44(1) (2) (3)解 (1)中有向哈密尔顿通路,例如4231v v v v . 但无有向哈密尔顿回路. (2)中有有向哈密尔顿回路,例如13421v v v v v ,所以,(2)是有向哈密尔顿图. (3)有有向哈密尔顿通路,如12543v v v v v . 但无有向哈密尔顿回路.虽然哈密尔顿回路问题与欧拉回路问题在形式上极为相似,但是,到目前为止,人们还没有找到哈密尔顿图(或有向哈密尔顿图)的充分必要条件.下面仅就无向图,给出判断哈密尔顿通路和哈密尔顿图的一些充分条件和必要条件.定理 (1)设n (>2)阶简单图G 的每一对不邻接的结点度数之和都大于或等于n-1,则G 中存在哈密尔顿通路.(2)设n (>3)阶简单图G 的每一对不邻接的结点度数之和都大于或等于n ,则G 中存在哈密尔顿回路,即G 是哈密尔顿图。

哈密尔顿图的判定及应用论文哈密尔顿图的判定及应用论文引导语:哈密尔顿图的研究是图论中不可或缺的一部分,这个问题的研究已经应用到了各个领域。
合理的利用哈密尔顿图的结论,不仅可以节约大量的时间,更可以降低发展的成本。
因此很多学者致力于哈密尔顿图的问题研究,也得到了很多了不起的突破。
1 引言在查阅了大量资料后,可以发现哈密尔顿图在数学理论研究和现实应用中都具有重要的地位。
哈密尔顿图的研究解决了大量的问题,但是还是有很多的问题还未得到解决。
其中较为著名的就是关于货郎担问题的解决方案,至今还没有很好的答案。
本文在综合了各种哈密尔顿图的判定方法之后,尝试用多种方法去解决货郎担问题,在比较后,找到一种相对较好的方法,也为将来的继续研究提供研究方向。
1.1 哈密尔顿图的起源哈密尔顿(Hamilton)是一位出生在爱尔兰的天文学家和数学家. 他的一生是很丰富多彩的,自从他发现“四元数”后,他又发现了另一种称之为“The Icosian Calculus”的代数系统,这个系统包含有乘法和加法的运算算子,但是乘法并不满换律(即xy-yx这个规律)。
他发现的这个代数系统是和正则12 面体有关的。
于是在1859 年他提出下列周游世界的游戏:在正十二面体的二十个顶点上依次标记伦敦、巴黎、莫斯科、华盛顿、北京、东京等世界著名大城市; 正十二面体的棱( 边) 表示连接这些城市的路线。
问: 能否在图中做一次旅行,从顶点到顶点, 沿着边行走, 经过每个城市恰好一次之后再回到出发点?曾经有很多人不断追寻这个游戏的答案。
可以应用拓扑的思想,将这正十二面体“拉平”将会得到一个和它同构的平面图(如图1-1),这样进行就可以将这个游戏转化为:要求必须沿着正十二面体的棱,怎样才能走完正则十二面体上的所有顶点,而且最后又回到起点的问题。
图1-1:哈密尔顿周游世界图从此人们将这类图称作哈密尔顿图,哈密尔顿图的研究也开始慢慢建立起来。
1.2 研究背景和意义哈密尔顿图是图论的重要的一部分,随着数学和科学技术的蓬勃发展,它的应用已经渗透到自然科学、社会科学的各个领域。

图论中的哈密顿图与欧拉图图论是数学的一个分支,研究图的性质及其应用。
在图论中,哈密顿图和欧拉图是两个重要的概念。
本文将介绍哈密顿图和欧拉图的定义、性质和应用,并探讨它们在现实生活中的实际应用。
一、哈密顿图的定义与性质哈密顿图是指一种包含了图中所有顶点的路径的图。
具体来说,哈密顿图是一个简单图,其中任意两个不同的顶点之间都存在一条路径,使得该路径经过图中的每个顶点且不重复。
哈密顿图具有以下的性质:1. 哈密顿图是一个连通图,即图中的每两个顶点之间都存在通路。
2. 图中每个顶点都是度数大于等于2的点,即每个顶点都至少连接着两条边。
二、欧拉图的定义与性质欧拉图是指一种可以通过图中每条边恰好一次的路径来穿越图的图。
具体来说,欧拉图是一个简单图,其中经过图中每条边且路径不重复的路径称为欧拉路径,而形成闭合回路的欧拉路径称为欧拉回路。
欧拉图具有以下的性质:1. 每个顶点的度数都是偶数,即每个顶点都连接着偶数条边。
2. 欧拉图中至少有两个连通分量,即图中有至少两个不同的部分可以从一部分通过路径到达另一部分。
三、哈密顿图与欧拉图的应用哈密顿图和欧拉图在实际生活中有广泛的应用,下面将分别介绍它们的应用领域。
1. 哈密顿图的应用:哈密顿图在旅行商问题中有着重要的应用。
旅行商问题是指一个旅行商要依次拜访若干个城市,然后返回起始城市,而要求找到一条最短的路径使得每个城市都被访问一次。
哈密顿图可以解决这个问题,通过寻找一条哈密顿路径来确定最短的路径。
2. 欧拉图的应用:欧拉图在电路设计和网络规划中发挥着重要的作用。
在电路设计中,欧拉图可以帮助我们确定如何安排电线的布线以最大程度地减少电线的长度和复杂度。
在网络规划中,欧拉图可以用于确定如何正确地连接不同的网络节点以实现高效的信息传输。
四、结论哈密顿图和欧拉图是图论中的两个重要概念。
哈密顿图是一种包含了图中所有顶点的路径的图,而欧拉图是一种可以通过图中每条边恰好一次的路径来穿越图的图。

哈密尔顿图的充分必要条件摘要图论在现实生活中有着较为广泛的应用, 到目前为止,哈密尔顿图的非平凡充分必要条件尚不清楚,事实上,这是图论中还没解决的主要问题之一,但哈密尔顿图在实际问题中,应用又非常广泛,因此哈密尔顿图一直受到图论界以及运筹学学科研究人员的大力关注.关键词:哈密尔顿图;必要条件;充分条件;1 引言 (4)2 哈密尔顿图的背景 (4)3 哈密尔顿图的概念 (5)4 哈密顿图的定义 (6)4.1定义 (6)4.2定义 (6)4.3哈密顿路是遍历图的所有点。
(7)4 哈密尔顿图的充分条件和必要条件的讨论 (8)5 结论 (9)参考文献 (9)指导老师 (10)1 引言图论是一门既古老又年轻的学科,随着科学技术的蓬勃发展,它的应用已经渗透到自然科学以及社会科学的各个领域之中,利用它我们可以解决很多实际生活中的问题,给你一个图,你怎么知道它是否是哈密尔顿图呢?当然如果图的顶点不多,你可以用最古老的”尝试和错误”的方法试试找哈密尔顿回路就可以解决和判断.但是,数学家们并不满足这样的碰得焦头烂额后才找到的真理方法.是否存在一组必要和充分的条件,使得我们能够简单轻易地判断一个图是否是哈密尔顿图?有许多智者通过各种方式去尝试过了,遗憾的是至今尚未找到一个判别哈密尔顿回路和通路的充分必要条件.虽然有些充分非必要或必要非充分条件,但大部分还是采用尝试的办法,不过这些条件也是非常有用的.2 哈密尔顿图的背景美国图论数学家奥在1960年给出了一个图是哈密尔顿图的充分条件:对于顶点个数大于2的图,如果图中任意两点度的和大于或等于顶点总数,那这个图一定是哈密尔顿图。
闭合的哈密顿路径称作哈密顿圈,含有图中所有顶的路径称作哈密顿路径.1857年,哈密尔顿发明了一个游戏(Icosian Game).它是由一个木制的正十二面体构成,在它的每个棱角处标有当时很有名的城市。
游戏目的是“环球旅行”。
为了容易记住被旅游过的城市,在每个棱角上放上一个钉子,再用一根线绕在那些旅游过的城市上(钉子),由此可以获得旅程的直观表示(如图1)。
哈密顿图十二面体中地哈密顿路径哈密顿图(英语:Hamiltonian path,或Traceable path)是一个无向图,由天文学家哈密顿提出,由指定地起点前往指定地终点,途中经过所有其他节点且只经过一次.在图论中是指含有哈密顿回路地图,闭合地哈密顿路径称作哈密顿回路(Hamiltonian cycle),含有图中所有顶地路径称作哈密顿路径.美国图论数学家奥勒在1960年给出了一个图是哈密尔顿图地充分条件:对于顶点个数大于2地图,如果图中任意两点度地和大于或等于顶点总数,那这个图一定是哈密尔顿图.哈密尔顿回路问题与欧拉回路类似. 它是1859年哈密尔顿首先提出地一个关于12面体地数学游戏:能否在图10.4.9中找到一个回路,使它含有图中所有结点一次且仅一次?若把每个结点看成一座城市,连接两个结点地边看成是交通线,那么这个问题就变成能否找到一条旅行路线,使得沿着该旅行路线经过每座城市恰好一次,再回到原来地出发地呢?为此,这个问题也被称作周游世界问题(10.4.9)对图10.4.9 , 图中粗线给出了这样地回路.定义10.4.3 给定图G, 若有一条路通过G中每个结点恰好一次, 则这样地路称为哈密尔顿路;若有一个圈, 通过G个每个结点恰好一次, 这样地圈称为哈密尔顿回路(或哈密尔顿圈). 具有哈密尔顿回路地图称为哈密尔顿图.尽管哈密尔顿回路与欧拉回路问题在形式上极为相似,但是到目前为止还不知道一个图为哈密尔顿图地充要条件,寻找该充要条件仍是图论中尚未解决地主要问题之一.下面先给出一个简单而有用地必要条件.定理10.4.4 设图G=〈V ,E〉是哈密尔顿图, 则对于V地每个非空子集S, 均有W(G-S)≤|S| 成立, 其中W(G-S)是图G-S地连通分支数.证明: 设α是G地哈密尔顿回路, S是V地任一非空子集. 在G-S中, α最多被分为|S|段, 所以W(G-S)≤|S|利用本定理可判别某些图不为哈密尔顿图. 如在图10.4.10中, 若取S={v1, v4}, 则G -S有3 个连通分支, 故该图不是哈密尔顿图.判断哈密尔顿图地充分条件很多, 我们仅介绍其中一个.定理10.4.5 设G=〈V ,E〉是有n个结点地简单图,1)如果任两结点u, v∈V, 均有deg(u)+deg(v)≥n-1,则在G中存在一条哈密尔顿路;2)如果对任两结点u, v∈V, 均有deg(u)+deg(v)≥n,则G是哈密尔顿图. 证明略.【例10.4.3】某地有5个风景点.若每个景点均有两条道路与其他景点相通,问是否可经过每个景点恰好一次而游完这5处?解将景点作为结点,道路作为边,则得到一个有5个结点地无向图.由题意,对每个结点vi,有deg(vi)=2(i∈N5).则对任两点vi, vj(i, j∈N5)均有deg(vi)+deg(vj)=2+2=4=5-1 可知此图一定有一条哈密尔顿路,本题有解.我们再通过一个例子,介绍一个判别哈密尔顿路不存在地标号法.【例10.4.4】证明图10.4.11所示地图没有哈密尔顿路.证明: 任取一结点如v1,用A标记,所有与它相邻地结点标B.继续不断地用A标记所有邻接于B 地结点,用B标记所有邻接于A地结点,直到图中所有结点全部标记完毕.如果图中有一条哈密尔顿路,则必交替通过结点A和B.因此或者结点A和B数目一样,或者两者相差1个.(10.4.11)而本题有3个结点标记A,5个结点标记B,它们相差2个,所以该图不存在哈密尔顿路.作为哈密尔顿回路地自然推广是著名地货郎担问题.问题是这样叙述地:设有一个货郎,从他所在地城镇出发去n-1个城镇.要求经过每个城镇恰好一次,然后返回原地,问他地旅行路线怎样安排才最经济?从图论地观点来看,该问题就是:在一个有权完全图中找一条权最小地哈密尔顿回路.研究这个问题是十分有趣且有实用价值地.但很可惜,至今没有找到一个很有效地算法.当然我们可以用枚举法来解,但是当完全图地结点较多时,枚举法地运算量在计算机上也很难实现.下面介绍地“最邻近方法”给出了问题地近似解.最邻近方法地步骤如下:1) 由任意选择地结点开始, 找与该点最靠近(即权最小)地点, 形成有一条边地初始路径.2) 设x表示最新加到这条路上地结点, 从不在路上地所有结点中选一个与x最靠近地结点, 把连接x与这一结点地边加到这条路上. 重复这一步, 直到G中所有结点包含在路上.3) 将连接起始点与最后加入地结点之间地边加到这条路上, 就得到一个圈, 即为问题地近似解.【例10.4.5】某流动售货员居住在a城,为推销货物他要访问b,c,d城后返回a城.若该4城间地距离如图10.4.12所示,试用最邻近方法找出完成该旅行地最短路线?解按最邻近方法一共有4步,见图10.4.13. 得到地总距离为46.(10.4.12)寻找哈密顿路径是一个典型地NP-完全问题.后来人们也证明了,找一条哈密顿路地近似比为常数地近似算法也是NP-完全地.寻找哈密顿路地确定算法虽然很难有多项式时间地,但是这并不意味着只能进行时间复杂度为O(n!*n)暴力搜索.利用状态压缩动态规划,我们可以将时间复杂度降低到O(2^n*n^3),具体算法是建立方程f[i][S][j],表示经过了i个节点,节点都是集合S地,到达节点j时地最短路径.每次我们都按照点j所连地节点进行转移.哈密顿路图论在许多领域,诸如物理、化学、运筹学、计算机科学、信息论、控制论、网络理论、社会科学以及经济管理等各方面都有广泛地应用,它已经广泛地应用于实际生活、生产和科学研究中.所以作为二十一世纪地应用型,我们应该好好学习图论,把图论应用到现实生活中,帮我们解决一些实际生活中地问题,让所学地知识更好地服务于我们.。