离散数学(7.4欧拉图与汉密尔顿图)
- 格式:ppt
- 大小:615.00 KB
- 文档页数:43









欧拉图和哈密顿图是离散数学中的两个重要的图论概念。
它们分别研究了图中的路径问题,对于解决一些实际问题具有很大的应用价值。
欧拉图是指一个无向图中存在一条路径,经过图中的每条边一次且仅一次,这条路径称为欧拉路径。
如果这个路径的起点和终点重合,则称为欧拉回路。
而对于有向图,存在一条路径,使得经过每一个有向边恰好一次,称为欧拉有向路径,如果该路径起点和终点相同,则称为欧拉有向回路。
1722年,瑞士数学家欧拉首次提出了这个概念,并证明了一系列欧拉图的性质。
欧拉图的性质是其路径的存在性。
既然有了这个概念,那如何判断一个图是不是欧拉图就是一个非常重要的问题。
根据欧拉图的定义,我们可以发现,图中的每个节点的度数都应该是偶数,否则该节点无法成为路径中的中间节点。
因此,一个图是欧拉图的充分必要条件是该图中每个节点的度数都是偶数。
哈密顿图是指一个图中存在一条路径,经过图中的每个顶点一次且仅一次,这条路径称为哈密顿路径。
如果这个路径的起点和终点重合,则称为哈密顿回路。
哈密顿图的概念由19世纪初英国数学家哈密顿引入,其研究对象是关于骑士巡游问题。
与欧拉图不同的是,哈密顿路径并没有一个十分明显的判定条件。
唯一已知的是某些图是哈密顿图,比如完全图和圈图。
至于一般的图是否存在哈密顿路径,目前尚无通用的判定方法。
这也是全世界许多数学家所面临的一个著名且具有挑战性的开放问题,被命名为“哈密顿路径问题”。
欧拉图和哈密顿图在实际问题中具有广泛的应用。
欧拉图的应用包括电子电路和网络的设计,路线规划等。
而哈密顿图的应用更多地涉及路径的优化问题,比如旅行商问题。
在实际应用中,我们常常需要通过对欧拉图和哈密顿图的研究,来寻找最优解或者设计最佳路径。
总的来说,离散数学中的欧拉图和哈密顿图是两个重要的图论概念,它们研究的是图中的路径问题。
欧拉图的判定条件相对明确,而哈密顿图的判定则是一个尚未完全解答的开放问题。
这两个概念在实际中具有广泛的应用,对于解决一些路径优化问题具有重要的参考价值。
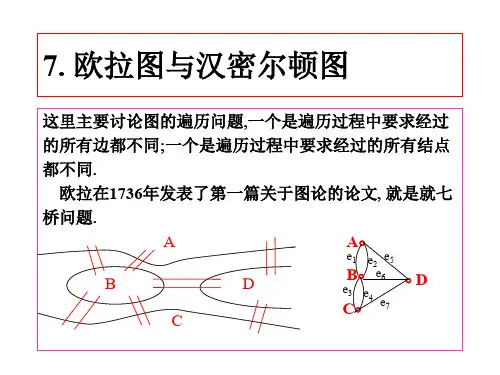
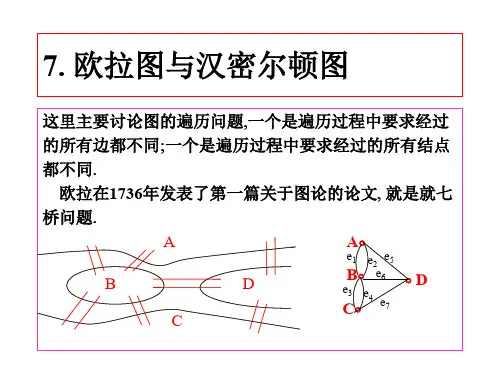
第四讲几种特殊图一、小结本讲主要介绍欧拉图与汉密尔顿图、平面图与着色以及一些相关的概念与结论等。
1.欧拉图的概念给定无孤立结点图G ,若存在一条路经过图G的每条边一次且仅一次,则该路称为欧拉路;若存在一条回路经过图G的每条边一次且仅一次,在该回路称为欧拉回路;具有欧拉回路的图称为欧拉图;具有欧拉路但无欧拉回路的图称为半欧拉图。
规定平凡图为欧拉图。
2.欧拉路与回路存在的充要条件无向图G具有一条欧拉路,当且仅当G是连通的,且有零个或2个奇数度数的结点。
无向图G具有一条欧拉回路,当且仅当G是连通的,并且它的结点度数都是偶数的。
3.汉密尔顿图的概念给定图G ,若存在一条路经过图G的每个结点一次且仅一次,则该路称为汉密尔顿路;若存在一条回路经过图G的每个结点一次且仅一次,则该回路称为汉密尔顿回路;具有汉密尔顿回路的图称为汉密尔顿图;具有汉密尔顿路但无汉密尔顿回路的图称为半汉密尔顿图。
4.汉密尔顿回路存在的必要条件若图G=<V,E>中具有一条汉密尔顿回路,则对于结点集V的每个非空子集S均有W(G-S)£|S|成立,其中W(G-S)是(G-S)中连通分支数。
5.汉密尔顿路存在的充分条件设G=<V,E>是具有n个结点的简单图,若在G中每一对结点度数之和大于等于n - 1,则在G中存在一条汉密尔顿路。
6.平面图的概念设G=<V,E>是一个无向图,如果能把G的所有结点与边画在平面上,并且使得任何两条边除端点外没有其他的交点,则称G是一个平面图(也称可平面图).显然平面图的边与边只在结点处相交。
将平面图“图示在平面上”,有时也说成“将平面图嵌入一平面”。
7.平面图的面、边界、面的次数等概念设G是一个连通平面图,如果由图中的边所包围的一个区域内既不包含图的结点,也不包含图的边,则这个区域称为G的一个面,包围该面的所有边所构成的回路称为这个面的边界。
面r的边界的回路长度称为该面的次数,记为deg(r)。