计算方法——共轭梯度法求解线性方程组
- 格式:pdf
- 大小:256.87 KB
- 文档页数:5

共轭梯度法公式
共轭梯度法是一种用于求解线性方程组的迭代算法。
其主要思想是通过利用前一次迭代的信息来加速当前迭代的速度,从而减少迭代次数和计算量。
共轭梯度法公式包括以下几个步骤:
1. 初始化:设初始解为x0,残量b0为Ax0-b,共轭方向d0=b0。
2. 迭代求解:对于第k次迭代,计算步长αk,使得xk+1=xk+αkd,其中d是共轭方向,满足dTkAd=0,即d是A的共轭向量。
3. 更新残量:计算新的残量bk+1=Axk+1-b,如果bk+1小于预设精度,则停止迭代。
4. 更新共轭方向:计算新的共轭方向dk+1=bk+1+βkdk,其中βk=(bk+1)Tbk+1/(bk)Tbk,保证dk+1与之前的共轭方向都是A的共轭向量。
5. 重复迭代,直到满足收敛条件,返回最终解xk+1。
共轭梯度法是一种高效的求解大型线性方程组的方法,尤其适用于稀疏矩阵和对称正定矩阵。
公式简单易懂,容易实现,且具有较快的收敛速度。
- 1 -。

共轭梯度法和梯度下降法共轭梯度法和梯度下降法是两种常用的优化算法,它们在解决最优化问题时具有重要的作用。
本文将分别介绍共轭梯度法和梯度下降法的原理、优势和应用领域,并对它们进行比较和总结。
一、共轭梯度法共轭梯度法是一种迭代算法,用于求解线性最小二乘问题或者解线性方程组。
它的核心思想是通过迭代求解一系列的共轭方向,从而不断逼近最优解。
共轭梯度法的优势在于它能够充分利用问题的特殊结构,避免不必要的计算。
相比于梯度下降法,共轭梯度法通常收敛更快,并且对于大规模问题的求解效果更好。
共轭梯度法主要应用于求解线性方程组、最小二乘问题以及特定的优化问题,如信号处理、图像处理和机器学习等领域。
二、梯度下降法梯度下降法是一种基于梯度的迭代优化算法,用于求解无约束最优化问题。
它的核心思想是沿着负梯度方向不断迭代,直至达到最优解或者满足停止条件。
梯度下降法的优势在于它的简单性和易于实现性。
它不需要求解二阶导数,只需要计算一阶导数,因此对于大规模问题的求解也比较高效。
梯度下降法广泛应用于机器学习中的参数优化问题,如线性回归、逻辑回归和神经网络等。
此外,它还可以用于函数拟合、特征选择和降维等领域。
三、共轭梯度法与梯度下降法的比较共轭梯度法和梯度下降法都是常见的优化算法,它们的选择取决于具体的问题和需求。
1. 收敛速度:共轭梯度法通常比梯度下降法收敛更快。
共轭梯度法在每次迭代时利用了前面所有迭代步骤的信息,可以更快地逼近最优解。
2. 内存消耗:梯度下降法只需要存储当前的梯度信息,而共轭梯度法需要存储一系列的共轭方向。
因此,对于大规模问题,梯度下降法在内存消耗方面更具优势。
3. 线性方程组求解:共轭梯度法是一种求解线性方程组的有效方法,而梯度下降法通常不适用于求解线性方程组。
4. 二次型优化问题:共轭梯度法对于二次型优化问题的求解效果更好。
梯度下降法在处理非二次型问题时可能会出现收敛速度慢、局部最优等问题。
共轭梯度法和梯度下降法是两种常用的优化算法。

共轭梯度法步骤共轭梯度法是一种求解线性方程组的迭代算法,它以高效稳定的特点而广受欢迎。
以下是共轭梯度法的步骤:步骤1:初始化首先,我们需要有一个初始向量x0和一个初始残量r0=b-Ax0。
其中,A为系数矩阵,b为常数向量。
步骤2:计算方向向量令d0=r0,表示第一次迭代的方向向量。
步骤3:计算步进长度令α0=(r0·r0)/(d0·Ad0),其中·表示向量的点积。
α0表示迭代过程中每个方向向量的步进长度。
步骤4:更新解向量令x1=x0+α0d0,表示迭代后的解向量。
步骤5:计算新残量令r1=r0-α0Ad0。
步骤6:判断终止条件如果r1的范数小于预设阈值,或者迭代次数达到预设次数,终止迭代。
否则,进入下一次迭代。
步骤7:更新方向向量令β1=(r1·r1)/(r0·r0),表示更新方向向量的轴线。
步骤8:计算新方向向量令d1=r1+β1d0,表示新的迭代方向向量。
步骤9:计算新的步进长度令α1=(r1·r1)/(d1·Ad1)。
步骤10:更新解向量令x2=x1+α1d1。
步骤11:更新残量令r2=r1-α1Ad1。
步骤12:重复步骤6至11,直至满足终止条件。
总结起来,共轭梯度法的步骤主要包括初始化、计算方向向量、计算步进长度、更新解向量、计算新残量、判断终止条件、更新方向向量、计算新的步进长度、更新解向量和更新残量等。
该算法迭代次数较少,收敛速度快,适用于大规模线性方程组的求解。


共轭梯度法prp共轭梯度法prp是求解线性方程组Ax=b的一种有效方法,它具有收敛速度快的优点,在计算机科学、经济学等领域被广泛应用。
在本文中,我们将分步骤阐述共轭梯度法prp的原理和算法流程,并探讨它的一些优缺点。
一、共轭梯度法prp的原理:求解线性方程组Ax=b的时候,如果我们采用梯度下降法,每次迭代时都是从当前点xk出发,按照负梯度方向向下移动一定距离得到下一个点xk+1。
如果点的数目很大,那么求解所需的时间也相应很长。
共轭梯度法prp则是在迭代过程中,每一次移动的方向都是共轭的,这样可以提高迭代收敛的速度。
二、共轭梯度法prp的算法流程:共轭梯度法prp的算法过程非常简单,我们可以用以下五个步骤来描述它的基本流程。
1.初始化:设xi=0,ri=b,pi=ri,i=0。
2.迭代:当i<n时,执行以下操作:(a)计算αi=(ri,pi)/(Api,pi)。
(b)更新:xi+1=xi+αipi。
(c)计算ri+1=ri-αiApi。
(d)选择βi=(ri+1,ri+1)/(ri,ri)。
(e)计算pi+1=ri+1+βipi。
3.输出结果。
三、共轭梯度法prp的优缺点:共轭梯度法prp与梯度下降法相比具有许多优点。
例如,它收敛速度快、计算复杂度低等等。
但是也存在一些缺点。
例如,收敛速度可以很快,但是随着迭代次数的增加,其收敛速度会逐渐变慢,甚至可能陷入振荡状态。
此外,如果矩阵的条件数太大,则共轭梯度法prp 的效果会变得很差,需要使用其他方法来求解方程组。
总之,共轭梯度法prp是求解线性方程组Ax=b的一个优秀方法,它可以提高计算速度和准确度。
尽管存在一些缺点,但共轭梯度法prp 仍是一个值得推崇的算法。

共轭梯度(CG)算法共轭梯度(Conjugate Gradient, CG)算法是一种用于求解线性方程组的迭代算法。
它主要用于求解对称正定矩阵的线性方程组,如最小二乘问题、PDE(偏微分方程)问题等。
CG算法通过利用矩阵的对称性和正定性,以及向量的共轭关系,实现了高效的求解线性方程组的能力。
CG算法的基本思想是通过一系列共轭的方向,逐步逼近方程组的解。
它利用了矩阵的特性,减少了计算量和存储需求,并且具有较快的收敛速度。
下面将介绍CG算法的原理和过程。
首先,假设我们要求解一个线性方程组Ax=b,其中A是对称正定矩阵,b是已知向量,x是待求解向量。
我们通过迭代的方式逼近x的解,即x(k)。
CG算法的迭代过程如下:1.初始化:选择一个初始解x(0),设置r(0)=b-Ax(0),p(0)=r(0),k=0;2. 迭代计算:计算步长alpha(k)和更新向量x(k+1):alpha(k) = (r(k)^T * r(k)) / (p(k)^T * A * p(k))x(k+1) = x(k) + alpha(k) * p(k)3. 计算残差向量r(k+1)和比例系数beta(k+1):r(k+1) = r(k) - alpha(k) * A * p(k)beta(k+1) = (r(k+1)^T * r(k+1)) / (r(k)^T * r(k))4.更新方向p(k+1):p(k+1) = r(k+1) + beta(k+1) * p(k)5.终止条件判断:如果满足终止条件,停止迭代;否则,令k=k+1,返回步骤2在CG算法中,为了降低数值误差和迭代次数,通常会使用预条件技术,如Jacobi预条件、不完全Cholesky预条件等。
预条件技术可以通过对矩阵进行适当的近似,加速算法的收敛。
CG算法的收敛性和效率主要与矩阵的条件数有关。
对于条件数较大的矩阵,CG算法的迭代次数会增加,收敛速度会减慢。
因此,在实际应用中,通常会选择合适的预条件技术和求解策略,以提高CG算法的效率和稳定性。


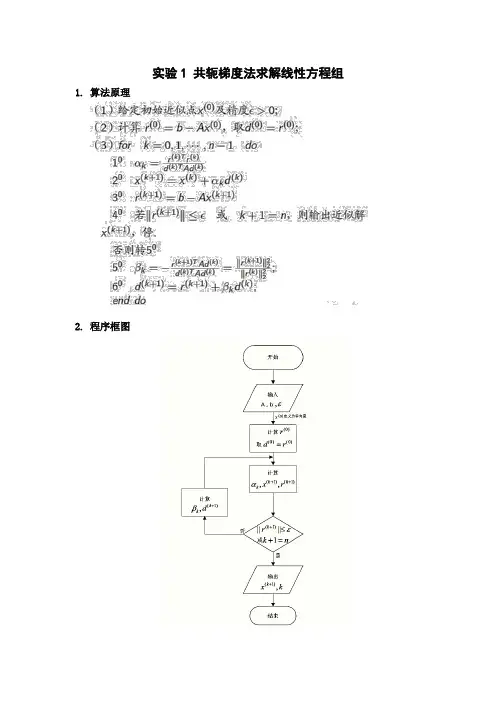
实验1 共轭梯度法求解线性方程组1.算法原理2.程序框图3.程序使用说明。
本程序使用MATLAB来求解线性方程组Ax b源程序文件“gongetidu1.m”为共轭梯度法源程序,x为方程组的解,k为迭代次数,A为方程组的系数矩阵,b为方程组的右端项,ep为精度。
定义A, b,ep后,在命令窗口输入[x,k] = gongetidu1(A,b,ep),回车后即可算出方程组的解和迭代次数。
源程序文件“gongetidu2.m”为共轭梯度算例3.2中构造A,b矩阵的程序。
定义阶数n的数值后,在命令窗口输入[A,b] = gongetidu2(n)即可算出A, b矩阵。
4.算例计算结果此算例为课本113页计算实习3.2.首先,设定MATLAB的数值格式为“long”。
当n=100时,在命令窗口中输入“[A,b]=gongetidu2(100)”,回车后可得到A 和b的矩阵;假设精度ep = 10-3,然后在命令窗口输入“[x,k] = gongetidu1(A,b,10^-3)”即可算出方程组的解x和迭代次数k。
x=( 0.999999999999988,0.999999999999995,1.000000000000009,···0.9999 99999999997,0.999999999999998 )T(x向量一共有100个元素)k=49.同理,可以算出n=200,400的结果。
n=200时,同样假设精度ep = 10-3,结果为:x=( 0.999999999999974,1.000000000000023,0.999999999999935,···1.000000 000000029, 0.999999999999987)T (x向量一共有200个元素)k=99.n=400时,同样假设精度ep = 10-3,结果为:x=( 1.000000000000017,0.999999999999846,1.000000000000039,···0.99999999 9999881,1.000000000000062)T (x向量一共有400个元素)k=199。


利用共轭梯度法求解线性方程组翟莹1012205052在自然科学和工程技术中很多问题的解决常常归结为解线性方程组,而这些方程组的系数矩阵大致可分为两种:低阶稠密矩阵和大型稀疏矩阵。
而求解方程组的方法通常为直接法和迭代法。
直接法用于较低阶方程组的求解,效率较高;迭代法更适用于高阶方程组的求解,常用的经典迭代法有高斯-赛德尔迭代法和雅各比迭代法,但收敛效率较低;共轭梯度法(CG)以较高的收敛速度而经常被采用。
从理论上讲,一个n阶方程组最多迭代n 步就可求出精确解。
1 直接法直接法就是经过有限步算术运算,无需迭代可直接求得方程组精确解的方法。
但实际计算中由于舍入误差的存在和影响,这种方法也只能得到线性方程组的近似解,该方法是求解低阶稠密矩阵方程组的有效方法。
如Cramer法则,Gauss消元法及其变形(LU分解法、Cholesky 分解法、QR分解法)等。
Matlab中,用矩阵除法“/”或“\”直接求解线性方程组(见附录一),它是一个内部包含着许许多多的自适应算法,对超定方程用最小二乘法求解;对欠定方程因为它的解不唯一,Matlab给出所有解中范数最小的一个特解;对于三对角阵方程组,采用追赶法求解。
2 迭代法迭代法就是用某种极限过程去逐步逼近线性方程组精确解的方法。
该方法具有对计算机的存贮单元需求少,程序设计简单、原始系数矩阵在计算过程中不变等优点,是求解大型稀疏矩阵方程组的重要方法。
迭代法不是用有限步运算求精确解,而是通过迭代产生近似解逼近精确解。
如Jacobi迭代、Gauss-Seidel迭代、SOR迭代法等。
在科学研究和大型工程设计中提出的求解问题,经离散后,常常归结为求解形如Ax = b 的大型线性方程组,此时系数矩阵A和b是通过测量或其它方法得到的,但是在多数情况下方程可能是病态的,即A的条件数非常大。
此时,我们仍然用Matlab中的常规算法,得到的解则可能不是真解。
通常情况下,对系数矩阵A和方程的右端b作微小的扰动,再用上述方法求解,扰动后方程组的解与原方程组的解相差甚远。
共轭梯度方法(Conjugate Gradient Method)是求解线性方程组的一种迭代算法。
该方法适用于求解大型稀疏的对称正定线性方程组,可以显著减少计算量和存储空间。
该方法的主要思想是利用共轭方向(Conjugate Directions)的性质,在有限次迭代中求解方程组的解。
共轭梯度方法的基本步骤如下:
选取一个初值$x_0$,并令$r_0=b-Ax_0$,其中$b$ 为方程组的右端向量,$A$ 为系数矩阵。
计算一个共轭方向$p_0=r_0$,即$p_0$ 与$r_0$ 正交,并满足$Ap_0 \neq 0$。
对于$k=0,1,2,\ldots$,执行以下操作:
a. 计算$\alpha_k=\frac{r_k^Tr_k}{p_k^TAp_k}$。
b. 更新解向量$x_{k+1}=x_k+\alpha_kp_k$。
c. 计算残差向量$r_{k+1}=r_k-\alpha_kAp_k$。
d. 计算$\beta_k=\frac{r_{k+1}^Tr_{k+1}}{r_k^Tr_k}$。
e. 更新共轭方向$p_{k+1}=r_{k+1}+\beta_kp_k$,即$p_{k+1}$ 与$p_k$ 具有共轭性。
如果残差向量$r_k$ 较小,则停止迭代,输出解向量$x_k$。
共轭梯度方法具有收敛速度快、存储空间小等优点,但对于非对称和非正定的线性方程组,该方法可能不收敛。
同时,该方法也有一些变体,如预处理共轭梯度法、共轭残差法等,可以更好地解决不同类型的线性方程组求解问题。
共轭梯度法1. 算法原理求解一个系数矩阵为正定矩阵的线性方程组可通过求泛函)(x f 的极小值点来获得,进而可以利用共轭梯度法来求解。
共轭梯度法中关键的两点是,确定迭代格式)()()1(k k k k d x x α+=+中的搜索方向)(k d 和最佳步长k α。
实际上搜索方向)(k d是关于矩阵A 的共轭向量,在迭代中逐步构造之;步长k α的确定原则是给定迭代点)(k x 和搜索方向)(k d 后,要求选取非负数k α,使得)()()(k k k d x f α+达到最小,即选择0≥k α,满足)(min )()()(0)()(k k k k k d x f d x f kααα+=+≤。
设迭代点)(k x和搜索方向)(k d已经给定,k α可以通过一元函数)()()()(k k d xf g αα+=的极小化)()(min )()(0k k d xf g ααα+=≤来求得,所以最佳步长)()()()(k k k k k Addd r TT=α。
在给定初始向量)0(x 后,由于负梯度方向是函数下降最快的方向,故第1次迭代取搜索方向)0()0()0()0()(Ax b x f r d-=-∇==。
令)0(0)0()1(d x x α+=,其中)0()0()0()0(0Addd r TT=α。
第2次迭代时,从)1(x 出发的搜索方向不再取()1r,而是选取)0(0)1()1(d r d β+=,使得)1(d与()0d 是关于矩阵A 的共轭向量,即要求)1(d 满足()()()0,01=Ad d ,由此可求得参数)0()0()0()1(0-Ad d Ad r TT=β,然后从()1x 出发,沿方向)1(d进行搜索得)1(1)1()2(d x xα+=,其中1α已由上面k α的计算式获得。
一般地,设已经求出)()()1(k k k k d x x α+=+,计算)1()1(++-=k k Ax b r。
共轭梯度法是一种常用的迭代方法,用于求解线性方程组Ax = b。
它适用于对称正定矩阵的情况,可以高效地求解大规模的线性方程组。
下面是使用共轭梯度法求解方程组的一般步骤:1. 初始化:选择一个初始解x0 和初始残差r0 = b - Ax0,设置初始搜索方向d0 = r0。
2. 迭代计算:进行迭代计算,直到满足停止准则(如残差的大小或迭代次数达到一定阈值)为止。
a. 计算步长αk = (rk^T rk) / (dk^T A dk),其中rk = b - A xk 是当前的残差。
b. 更新解xk+1 = xk + αk dk。
c. 计算新的残差rk+1 = rk - αk A dk。
d. 计算新的搜索方向dk+1 = rk+1 + (rk+1^T rk+1) / (rk^T rk) dk。
e. 更新迭代次数k = k + 1。
3. 输出解:当满足停止准则时,输出最终的解x。
需要注意的是,共轭梯度法的效率和收敛速度与矩阵的条件数有关。
对于病态矩阵或条件数较大的情况,可能需要进行预处理或使用其他更适合的求解方法。
此外,共轭梯度法还可以应用于非线性方程组的求解,采用牛顿法等方法来迭代求解。
在实际应用中,可以使用现有的数值计算库或软件来实现共轭梯度法,以提高计算的效率和精度。