福建省大田一中2011-2012学年高二暑假作业数学(理)试题(6)

福建省大田一中2011-2012 学年高一下学期阶段考试数学试题（平行班）一、选择题（共 10 小题，每题 5 分，共 50 分 . 只有一个选项是切合题目要求的）1、设M 2a(a 2), N (a 1)(a 3), 则有（）A ．M NB ． M N （等号定能取到）C．M N D ． M N （等号定能取到）2、在等差数列{ a n } 中， a3 a9 27 a6， S n表示数列 { a n} 的前 n 项和，则 S11( ) A．18 B．99 C．198 D ． 2973、若a,b, c为实数，则以下命题正确的选项是（）A．若 a b ，则 ac2 bc2 B．若 a b 0 ，则1 1a bC．若a b 0, 则 b a D ．若 a b 0 ，则 a2 ab b2a b4、已知ABC 知足 sin C 2cos B sin A ，则ABC 的形状是（）A．等腰三角形B．直角三角形 C ．等边三角形 D ．等腰三角形或直角三角形5、以下函数中，最小值为 4 的是（）A ．y x 4 （ x 3 ）B ．y sin x 4 (0 x )x sin xC ．y e x 4e xD ． y log3 x 4log x 36、记等比数列{ a n}的前 n 项和为 S n，若 S3＝ 2， S6＝ 18，则S10等于（）S5A ．3B ． 5C ． 31 D． 337、切合以下条件的三角形有且只有一个的是（）A ． a=1,b=2 ,c=3 B． a=1,b= 2 ,∠A=30°C． a=1,b=2, ∠ A=100° D ． b=c=1, ∠ B=45°8、假如数列{ a n}知足 : a1, a2 a1 ,a3 a2 ,..., a n a n 1 ,... 是首项为1，公比为 2 的等比数列，那么 a n等于（）。

A．2n 1 1 B ． 2n 1 C ． 2n 1 D ． 2n 19、北京 2008 年第 29 届奥运会开幕式上举行升旗仪式，在坡度15°的看台上，同一列上的第一排和最后一排测得旗杆顶部的仰角分别为60°和 30°，第一排和最后一排的距离为10 6 米（如下图），则旗杆的高度为( )。

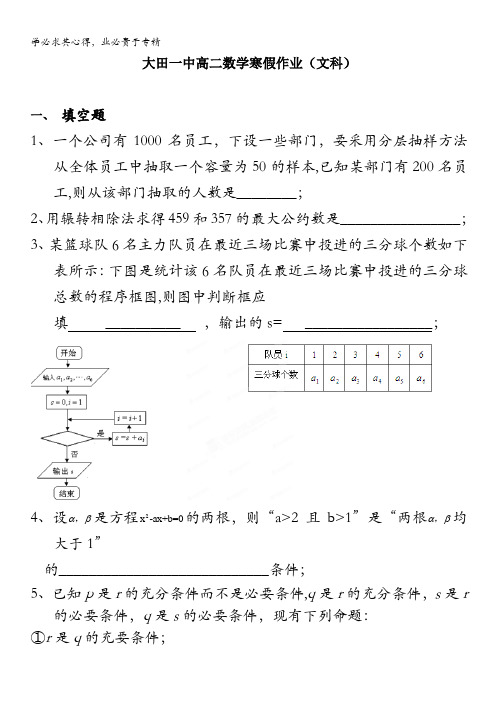
大田一中高二数学寒假作业（文科）一、填空题1、一个公司有1000名员工，下设一些部门，要采用分层抽样方法从全体员工中抽取一个容量为50的样本,已知某部门有200名员工,则从该部门抽取的人数是________；2、用辗转相除法求得459和357的最大公约数是________________；3、某篮球队6名主力队员在最近三场比赛中投进的三分球个数如下表所示：下图是统计该6名队员在最近三场比赛中投进的三分球总数的程序框图,则图中判断框应填__________ ，输出的s= _________________；4、设αβ，是方程2x-ax+b=0的两根，则“a>2且b>1”是“两根αβ，均大于1”的____________________________条件；5、已知p是r的充分条件而不是必要条件,q是r的充分条件，s是r的必要条件，q是s的必要条件，现有下列命题：①r是q的充要条件；②p 是q 的充分条件而不是必要条件； ③r 是q 的必要条件而不是充分条件; ④┐p 是┑s 的必要条件而不是充分条件； ⑤r 是s 的充分条件而不是必要条件。

则正确命题的序号是______________； 6、若动圆P 过定点A(—3，0），并且内切于圆C:（x-3)2+y 2=64，则动圆圆心P 点的轨迹是_____________________________________________________________________,出轨迹方程是______________________；7、焦点在x 轴上且焦距为6，经过点12(4,)5P 的椭圆的标准方程为_________________;8、某车间分批生产某种产品，每批的生产准备费用为800元.若每批生产x 件，则平均仓储时间为8x 天，且每件产品每天的仓储费用为1元。

为使平均到每件产品的生产准备费用与仓储费用之和最小,每批应生产产品_______________； 9、直线1y=x+b 2是曲线y=lnx 的一条切线，则实数b=__________；10、双曲线C与22x y-=1916有共同的渐近线，且过点，则C 的离心率为____；11、对于满足04P ≤≤的所有实数p ，使不等式2430px p xx -+-+>恒成立，则x12、函数2(3)1y mxm x =+-+的图象与x 轴的交点至少有一个在原点的右侧，则m 的取值范围为______________________；13、设双曲线的一个焦点为F ，虚轴的一个端点为B ,如果直线FB 与该双曲线的一条渐近线垂直，那么此双曲线的离心率为______________；14、若点P 在曲线41x y e =+上,α为曲线在点P 处的切线的倾斜角，则α的取值范围是____________________；15、抛物线2x y=-2与过点M （0，—1)的直线L 交于A 、B 两点，O 为坐标原点，若OA 、OB 的斜率之和为1，则直线L 的方程为_______________________；二、 解答题1、方程2212132x y m m+=--表示（1）椭圆，求m 的值；（2）焦点在y 轴上的椭圆，求m 的值;2、设P ：关于x 的不等式xa>1的解集是{x|x<0}；q ：函数2y=lg(ax -x+a)的定义域为R ，且p 、q 有且只有一个正确，求实数a 的取值范围；3、已知F 1，F 2是椭圆221169x y +=的左右焦点，P是椭圆上的一个动点，若延长F 1P 到Q ，使得|PQ|=|PF 2|,问动点Q 的轨迹是什么?并求出轨迹方程；4、甲乙两人约定上午7：00到8:00之间到某个汽车站乘车,在这段时间内有3班公共汽车，开车的时间分别为7：20,7：40，8：00，若他们约定，见车就乘，求两人同乘一班车的概率;5、某初级中学共有学生2000名,各年级男、女生人数如下表. 已知在全校学生中随Array机抽取1名,抽到初二年级女生的概率是0。

Exercise 6一．单选1。

---How do you think Kate can make it up with Laura?—--Set aside _____ they disagree and try to find ______ they have in common.A。

what，what B. where，what C. what , whether D。

where，whether2.Anne felt tired and terrible，which was ____ she was late for the chemistry examination，A. whyB. whereC. whether d. what3。

He must be helping the old man to water the flowers，______？A. is he？B。

isn’t he？ C. must he D. mustn’t he4.--—Did you go to the show last night?—-—Yeah。

Every body and girl in the area _____ invited。

A。

were B。

have been C. has been D。

was5。

I think you must be mistaken about seeing our teacher at the theatre, I'm sure he ___ abroad all week.A. isB. wasC. has been D。

had been6. The thief tried to break away from the policeman who _____ him, but failed.A。

has held B。

had held C. was holding D。

大田一中2012高二年级数学（理科）暑假作业（2）1.（Ⅰ）设2a a ∈≠-R 且，试比较222a a -+与的大小．（Ⅱ）求函数142y x x =-++的最大值．2.已知:|3|2,:(1)(1)0p x q x m x m -≤-+--≤，若p ⌝是q ⌝的充分而不必要条件，求实数m 的取值范围.3.已知集合Q P M n n n y y Q x x x x P =∈≤≤-===++=*},,21,12|{},0)2410(|{2N ， 在平面直角坐标系中，点A ),(y x ''的坐标M y M x ∈'∈',，试计算：(1) 点A 正好在第三象限的概率；（2）点A 不在y 轴上的概率；（3）点A 正好落在区域1022≤+y x 上的概率.5.已知∈c b a ,,+R ,,1=++c b a 求证：dx x c b a ⎰--≥---442161)11)(11)(11(π6.已知抛物线mx y =2)(R m ∈的焦点为)0,21(-F ，过点(0,2)A 的直线l 与抛物线mx y =2有且只有一个公共点，求直线l 的方程。

7．如图,有一块边长为1（百米）的正方形区域ABCD ,在点A 处有一个可转动的探照灯,其照射角PAQ ∠始终为45（其中点P ，Q 分别在边BC ，CD 上）,设,tan PAB t θθ∠==． （Ⅰ）用t 表示出PQ 的长度,并探求CPQ ∆的周长l 是否为定值．（Ⅱ）问探照灯照射在正方形ABCD 内部区域阴影部分的面积S 最大为多少（平方百米）?8、已知函数32ln )(+-=ax x a x f （0≠a ）.（Ⅰ）求函数)(x f 的单调区间; (Ⅱ）函数)(x f y =的图像在2=x 处的切线的斜率为,23若函数])([31)('23m x f x x x g ++=在区间（1，3）上不是单调函数，求 m 的取值范围。

大田一中高二数学（理科）寒假作业（一）一．选择题(本大题共10 小题,每小题5 分,共50 分）1、在如图所示的“茎叶图”表示的数据中,众数和中位数分别是( ）Ａ。

23 与26 B.31 与26C.24 与30 D。

26 与302、有一批产品，从中取出两件,设A=“两件产品全不是次品”,B=“两件产品全是次品",C=“两件产品不全是次品”，则下列结论正确的是( ）A．A 与C 互斥B．B 与C 互斥C．任两个均互斥D．任两个均不互斥3、问题：①某社区有500个家庭，其中高收入家庭125户，中等收入家庭280户，低收入家庭95户，为了了解社会购买力的某项指标，要从中抽出一个容量为100户的样本;②从10名学生中抽出3人参加座谈会。

方法:Ⅰ简单随机抽样法；Ⅱ系统抽样法Ⅲ分层抽样法问题与方法配对正确的是（) A．①Ⅲ；②ⅠB．①Ⅰ;②ⅡC．①Ⅱ;②ⅢD．①Ⅲ；②Ⅱ4、用样本估计总体，下列说法正确的是（）A．样本的结果就是总体的结果B．样本容量越大，估计就越精确C．样本的标准差可以近似地反映总体的平均状态D．数据的方差越大，说明数据越稳定5、右边的框图的功能是计算表达式则在①、②两处应填入（）A．n = 0 和n ≤10 B．n = 1 和n ≤10C．n = 0 和n < 10 D．n = 1 和n 〈106、为提高信息在传输中的抗干扰能力，通常在原信息中按一定规则加入相关数据组成传输，设定原信息为a0a1a2,a i∈｛0，1｝(i=0，1，2），传输信息为h o a o a1a2h1,其中h0=a0⊕a1，h1=h0⊕a2，⊕运算规则为：0⊕0=0 ，0⊕1=1 ，1⊕0=1 ，1⊕1=0，例如原信息为111，则传输信息为01111．传输信息在传输过程中受到干扰可能导致接收信息出错，则下列接收信息一定有误的是（）A．11010 B．01100 C．10111 D．00011 7．（2010·全国Ⅱ文，7）若曲线y＝x2＋ax＋b在点（0,b)处的切线方程是x－y＋1＝0,则( )A．a＝1,b＝1 B．a＝－1，b＝1 C．a＝1,b＝－1D．a＝－1，b＝－18．设f（x）,g(x）分别是定义在R上的奇函数和偶函数．当x<0时，f′(x)g(x)＋f(x）g′（x)〉0，且g（－3)＝0，则不等式f（x)g(x)〈0的解集是（)A．（－3，0）∪(3,＋∞)B．(－3,0）∪(0,3)C．（－∞,－3）∪(3，＋∞）D．（－∞，－3)∪(0,3)9．下面四图都是同一坐标系中某三次函数及其导函数的图象,其中一定不正确的序号是( ）A．①②B．③④C．①③D．①④10．已知f（x）＝x3＋bx2＋cx＋d在区间［－1，2］上是减函数，那么b＋c( )A．有最大值错误!B．有最大值－错误!C．有最小值错误!D．有最小值－错误!二、填空题(本大题共5 小题，每小题5 分，共25 分）11、把六进制数403 转化八进制数为___ __（8)12、甲,乙两人随意入住三间空房，则甲、乙两人、各住一间房的概率是___ ____。

高二暑假作业（六） 文学类（实用类）文本阅读 一、阅读下面的文字，完成1-4题。

三道人生试题 邱成立 上大学的第二年，学校开了一门课程叫《人生》。

开学第一天，第一次上《人生》课，李老师先做了个简单的自我介绍，说他叫李毅然，和我们的共和国同一天过生日。

在这个学校教学已经十多年了。

然后就说要进行一次摸底考试。

同学们听了都很奇怪，刚刚开学，还没有学到什么东西，怎么考试呢？ 李老师笑眯眯地说：“说起来是考试，其实也就是个小调查。

内容很简单，只有三道题目。

”李老师顿了顿，看大家还是一脸茫然不知所措的样子，脸上又堆满了笑容，说：“下面我开始出题了。

第一题，你们有谁记得父母的生日吗？”听了李老师的话，很多同学愣住了，只有少数几个女生举起了手。

李老师数了数举手的人数；轻轻地点了点头，又说：“学校有四个门卫，每两人一班轮流看大门，谁能说出其中两个人的名字？”这一下大家傻眼了。

虽然大家经常从校门口出入，也知道这几个门卫分别是赵师傅、李师傅、王师傅、张师傅，可具体到每个人叫什么名字，还真说不出来。

李老师看大家哑口无言的样子，又笑了，接着抛出了第三个问题：“你是否经常反省自己？”这一问，所有的同学都低下了头。

教室里静默了一会儿，李老师说话了：“《人生》这门课程，旨在引导我们树立正确的人生观、价值观和世界观，教导我们今后如何立身处世、做人成才。

今天的三道考题，可以说是对同学们做一个检验。

” “第二题，记住你身边每一个人的名字，尊重你身边的每一个人。

尊重别人才能得到别人的尊重。

尊重别人可以使自己宽厚。

基石宽厚才能负重，人心宽厚才能做大事业。

” “最后一题，如果你记不住父母的生日，又叫不出门卫的名字，那么，你就该反省自己了。

”说到这里，李老师又在黑板上写下了“反省”两个字，“反省促人进步，有反省才会有悔悟，有悔悟才会有进步，才会有成才的可能。

” 这一课使每一个同学终身难忘。

二十年后，全班同学在广州大酒店聚会。

班长让大家介绍一下自己二十年来的工作情况和生活情况，时间不超过一分钟。

1. 在复平面上，平行四边形ABCD 的三个顶点A 、B 、C 对应的复数分别为 ,1,42i i +. 求第四个顶点D 的坐标及此平行四边形的对角线的长.2. 若椭圆22110x y m +=与双曲线221y x b-=有相同的焦点，且椭圆与双曲线交于点P y ⎫⎪⎪⎝⎭，求椭圆及双曲线的方程.3.设有编号为1，2，3，4，5的五个球和编号为1，2，3，4，5的五个盒子，现将这五个球放入5个盒子内. （1）只有一个盒子空着，共有多少种投放方法？（2）没有一个盒子空着，但球的编号与盒子编号不全相同，有多少种投放方法？（3）每个盒子内投放一球，并且至少有两个球的编号与盒子编号是相同的，有多少种？投放方法？4. 已知命题A ：函数f (x )=x 2 – 4mx + 4m 2+ 2在区间[– 1, 3]上的最小值为2； 命题B ：不等式x + |x – m |>1对任意x ∈R 恒成立；命题C ：{x | m ≤x ≤2m +1}⊆{x | x 2 – 4≥0}。

（1）若A 、B 、C 中至少有一个为真命题，试求实数m 的取值范围；（2）若A 、B 、C 中恰有一个为假命题，试求实数m 的取值范围5.如图，三棱柱111C B A ABC -的各棱长均为2，侧面11B BCC ⊥底面ABC ，侧棱1BB 与底面ABC 所成的角为︒60．（Ⅰ）求直线C A 1与底面ABC 所成的角大小；（Ⅱ）在线段11C A 上是否存在点P ，使得平面⊥CP B 1平面11A ACC ？若存在，求出P C 1的长；若不存在，请说明理由．6．已知 f (x )为二次函数，且f (－1)＝2，f ′(0)＝0，⎠⎛01 f (x )d x ＝－2. (1)求 f (x )的解析式；(2)求 f (x )在[－1,1]上的最大值与最小值．7.已知椭圆C ：)0(12222>>=+b a by a x 的上顶点为A ，两个焦点为1F 、2F ，21F AF ∆为正三角形且周长为6. （Ⅰ）求椭圆C 的标准方程；（Ⅱ）已知圆O :222R y x =+，若直线l 与椭圆C 只有一个公共点M ，且直线l 与圆O 相切于点N ；求||MN 的最大值．8．已知函数f(x)=alnx+2x (a 为实常数).（Ⅰ）求函数f(x)在[1，e]上的最小值及相应的x 值；（Ⅱ）若存在x ∈[1，e]，使得f(x)≤(a+2)x 成立，求实数a 的取值范围.暑假作业（4）6．(1) f (x )＝6x 2－4. (2) f (x )min ＝－4； f (x )max ＝2 7. （Ⅰ）13422=+y x （Ⅱ）32||-≤MN 8．（Ⅰ）当2-≥a 时，)(x f 的最小值为1，相应的x 值为1；当222-<<-a e 时，)(x f 的最小值为2)2ln(2a a a --，相应的x 值为2a -；当22e a -≤时，)(x f 的最小值为2e a +， 相应的x 值为e ． （Ⅱ）x x x x a ln 22--≥（],1[e x ∈），a 的取值范围是),1[+∞-．。

1．某同学在做“用双缝干涉测定光的波长”的实验时，第一次分划板中心刻度线对齐第2条亮纹的中心时(如图6甲中的A)，游标卡尺的示数如图乙所示，第二次分划板中心刻度线对齐第6条亮纹的中心时(如图丙中的B)，游标卡尺的示数如图丁所示．已知双缝间距d＝0.5 mm，双缝到屏的距离l＝1 m，则：(1)图乙中游标卡尺的示数为________cm.(2)图丁中游标卡尺的示数为________cm.(3)所测光波的波长为________m(保留两位有效数字)．2．某收音机接受电磁波的波长范围在577m到182m之间，该收音机调谐电路的可变电容器的动片完全旋出时，回路的总电容为39pF，求：（1）该收音机接收的电磁波的频率范围是多少？（2）该收音机调谐电路的可变电容器的动片完全旋入时，电路的总电容是多大？3．某小型实验水电站输出功率是20 kW，输电线总电阻为6 Ω。

(1)若采用380 V输电，求输电线路损耗的功率(2)若改用5000 V高压输电，用户端利用n1∶n2＝22∶1的变压器降低，求用户得到的电压4．弹簧振子以O点为平衡位置在B、C两点之间做简谐运动.B、C相距20 cm.某时刻振子处于B点.经过0.5 s，振子首次到达C点.求：（1）振动的周期和频率（2）振子在5 s内通过的路程及5 s末位移大小（3）振子在B点的回复力大小跟它距O点4 cm处P点的回复力大小的比值5．如图的螺线管，横截面积为S、匝数为N、电阻为r ，螺线管与一根电阻为2 r 的金属丝连接，向右穿过螺线管的匀强磁场随时间变化的规律如图，求0至t0时间内：（1）通过金属丝的感应电流大小和方向（2）金属丝中感应电流产生的焦耳热量Q（3）金属丝中流过的感应电量q6．如图所示，匀强磁场的磁感应强度B＝0.5 T，边长L＝10 cm的正方形线圈abcd共100匝，线圈电阻r＝1 Ω，线圈绕垂直于磁感线的对称轴OO′匀速转动，角速度ω＝2π rad/s，外电路电阻R＝4 Ω.。

大田一中2016－2017学年高二下阶段考试卷数 学(理科)一．选择题：(本大题共12小题，每小题5分，共60分)1．设复数12,z z 在复平面内对应的点关于实轴对称，12i z =+，则12z z =( ) A ．1i + B ．34i 55+ C ．41i 5+ D ．41i 3+2．“e 是无限不循环小数，所以e 为无理数．”该命题是演绎推理中的三段论推理，其中大前提是( )A. 无理数是无限不循环小数B. 有限小数或有限循环小数为有理数C. 无限不循环小数是无理数D. 无限小数为无理数3．已知复数()2i 1R 1i 2a z a +=+∈-是纯虚数，则实数a 的值为( ) A. 1 B. 2 C. 3 D. 44．下面给出了关于复数的三种类比推理，其中类比错误的是( )①复数的乘法运算法则可以类比多项式的乘法运算法则； ②由向量a 的性质|a |2＝a 2可以类比复数的性质|z |2＝z 2； ③由向量加法的几何意义可以类比得到复数加法的几何意义． A ．② B ．①② C ．①③ D ．③5．下列几种推理中是演绎推理的序号为( )A ．由20＜22，21＜32，22＜42，…，猜想2n －1＜(n ＋1)2(n ∈N ＋) B ．半径为r 的圆的面积S ＝πr 2，单位圆的面积S ＝π C ．猜想数列111,,,122334⨯⨯⨯ …的通项为a n ＝1(1)n n +(n ∈N ＋) D ．由平面直角坐标系中，圆的方程为(x －a )2＋(y －b )2＝r 2推测空间直角坐标系中球的方程为(x －a )2＋(y －b )2＋(z －c )2＝r 26．已知M 是面积为1的△ABC 内的一点(不含边界)，若△MBC ，△MCA 和△MAB 的面积分别为x ，y ，z ，则1x ＋y＋x ＋y z 的最小值是( )A ．2B ．3C ．3.5D ．47．用反证法证明某命题时，对结论：“自然数a ，b ，c 中至少有一个偶数．”正确的反设为( )A ．a ，b ，c 中至少有两个偶数B ．a ，b ，c 都是奇数C ．a ，b ，c 中至少有两个偶数或都是奇数D ．a ，b ，c 都是偶数8．设S k ＝12k +＋13k +＋14k +＋…＋121k -（k ≥3，k ∈N *），则S k ＋1＝（ ）A ． S k ＋121k +B ．S k ＋12k ＋121k +C ．S k ＋12k ＋121k +－12k +D ．S k －12k －121k +A ．(4，3π)B ．(－4，3π) C ．(－4，3π) D ．(4，3π)10．要证：222210a b a b +--≤，只要证明（ ）A ．22210ab a b --≤ B ．4422102a b a b ++--≤C ．222()102a b a b +--≤ D ．22(1)(1)0a b --≥11．若0＜x 1＜x 2＜1，则( )A ．21x x e e -＞lnx 2－lnx 1B ．21x x e e -＜lnx 2－lnx 1C ．x 21x e ＞x 12x eD ．x 21x e ＜x 12x e12．已知函数()1,031,02x e x f x x x ⎧->⎪=⎨+≤⎪⎩，若m n <且()()f m f n =，则n m -的取值范围是( )A ．31[ln 2,ln]23+ B ．31[ln 2,ln )23+ C ．2(,ln 2]3 D ．231(,ln ]323+二．填空题：(本大题共4小题，每小题5分，共20分)13．已知340)ax y z a ++=>，且222x y z ++的最小值为1，则a 的值为＿＿＿＿．14．在矩形ABCD 中，对角线AC 与相邻两边所成的角为α，β，则有co s 2α＋co s 2β＝1．类比到空间中的一个正确命题是：在长方体ABCD －A 1B 1C 1D 1中，对角线AC 1与相邻三个面所成的角为α，β，γ，则co s 2α＋co s 2β＋co s 2γ＝＿＿＿＿．15．已知函数f (x )＝x 3＋ax 2＋bx ＋c ，若f (x )在区间(－1，0)上单调递减，则a 2＋b 2的取值范围为＿＿＿＿．16．对于函数f (x )给出定义：设f ′(x )是函数y ＝f (x )的导数，f ″(x )是函数f ′(x )的导数，若方程f ″(x )＝0有实数解x 0，则称点(x 0，f (x 0))为函数y ＝f (x )的“拐点”．某同学经过探究发现：任何一个三次函数f (x )＝ax 3＋bx 2＋cx ＋d (a ≠0)都有“拐点”；任何一个三次函数都有对称中心，且“拐点”就是对称中心．给定函数32115()33212f x x x x =-+-，请你根据上面探究结果，计算1232016()()()()2017201720172017f f f f ++++＝＿＿＿＿＿．三．解答题：(本大题共6小题，第17题10分，第18～22题，每小题12分，共70分)17．(Ⅰ)若圆x 2＋y 2＝4在伸缩变换⎩⎪⎨⎪⎧x ′＝λx y ′＝3y (λ>0)的作用下变成一个焦点在x 轴上，且离心率为45的椭圆，求λ的值；(Ⅱ)在极坐标系中，已知点A (2，0)，点P 在曲线C ：ρ＝2＋2cos θsin 2θ上运动，求P 、A 两点间的距离的最小值．18．已知函数()214f x x x =+--．(Ⅰ)求不等式()3f x ≥的解集M ；(Ⅱ)若a M ∈，求证：152x a x a ++-≥．20．设函数f (x )＝23xx axe +(a ∈R )(Ⅰ)若f (x )在x ＝0处取得极值，确定a 的值，并求此时曲线y ＝f (x )在点(1，f (1))处的切线方程；(Ⅱ)若f (x )在3，＋∞)上为减函数，可知：x 2＝6a 6-≤3，解得a ≥－92．因此a 的取值范围为：9[,)2-+∞．解法二：由f (x )在3，＋∞)上恒成立．令u (x )＝2361x xx -+-，u ′(x )＝223[(1)1](1)x x --+-＜0， ∴u (x )在hslx3y3h3，＋∞)上单调递减，∴a ≥u (3)＝－92． 因此a 的取值范围为：9[,)2-+∞．21．解析：(1)曲线C 的普通方程为22(1)3x y -+=，又cos ,sin x y ρθρθ==，所以曲线C 的极坐标方程为22cos 20,0ρρθθπ--=≤≤.(2)设11(,)P ρθ，则有22cos 20,3ρρθπθ⎧--=⎪⎨=⎪⎩，解得112,3πρθ==， 设22(,)Q ρθ，则有π2sin()0,33ρθπθ⎧++=⎪⎪⎨⎪=⎪⎩，解得223,3πρθ=-=，所以12||||5PQ ρρ=-=．22．解析：(1)2a =时，()()()F x f x g x =-1ln 2x x b x=---， ()()21120F x x x x'=+->，()()()22211212x x x x F x x x -++-'==， 解()0F x '>得01x <<，解()0F x '<得1x >，∴()F x 的单调增区间为()0,1，单调减区间为区间为()1,+∞． (2)设切点坐标为设切点坐标为0001,ln x x x ⎛⎫- ⎪⎝⎭，()211f x x x '=+，切线斜率()020011a f x x x '==+，又0001ln x ax b x -=+， ∴002ln 1b x x =--，∴020011ln 1a b x x x +=+-- 令()()211ln 10h x x x x x=+-->，()32121h x x x x '=-+232x x x +-=()()321x x x +-=，解()0h x '<得1o x <<，解()0h x '>得1x >， ∴()h x 在()0,1上递减，在()1,+∞上递增． ∴()()11h x h =-≥，∴a b +的最小值为1-． (3)法一：令()1ln 23G x x x x=--+， 由(1)知()()()max 10G x G ==，∴1ln 23x x x--≤.又1xe x +≥，∴5252212x ex -⎡⎤⎛⎫-+ ⎪⎢⎥⎝⎭⎣⎦≥()230x x =->∴521223ln x e x x x---≥≥，(两个等号不会同时成立)∴5212ln 0x ex x--+>． 法二：令()5212ln x P x ex x -=-+，()522112x P x e x x-'=--显然()P x '在()0,+∞上递增，()10P '<，()20P '> ∴()0P x '=在()0,+∞上有唯一实根*x ，且()*1,2x ∈，5*2*12x ex -=+()2*1x ， ∴()P x 在()*0,x 上递减，在()*,x +∞上递增， ∴()()*P x P x≥*5*2*12ln x ex x -=-+()*2**21ln xx x =+-21ln 2024>+-> ∴5212ln 0x e x x--+>．。

大田一中2012年暑期作业（四)区域分析A1．根据下述资料，结合所学知识，完成(1）～（5）题。

资料一：见下图资料二：西宁地区有一首歌谣：“古城气候总无常,一日须携四季装。

山下百花山上雪，日愁暴雨夜愁霜.”资料三：西宁是一座具有2100多年历史的高原古城，曾是古“丝绸之路"南路和“唐蕃古道”的必经之地，成为西北交通要冲和军事重镇。

资料四：（1）根据资料一，图示区域积温由东向西,原因是。

（2）根据资料二,简述歌谣反映出该地自然环境的主要特征。

(3)西宁形成和发展成为城市的自然原因是（填正确项字母)。

A．位于河谷、地形平坦B．河流供水充足C．政治中心D．历史悠久E．交通要道（4)根据资料四，青海省与同纬度的山东省相比，1990年至2000年人口增长率(大、小）。

根据两省的现状,可以推断出青海省环境承载力较小，列举其主要影响因素。

（5）从自然条件角度分析青海省经济发展的优势和不利因素.2．阅读下列材料，回答：材料一：印度乔塔那格浦尔工业区和中国的沪宁杭工业区图材料二：太湖平原与东北平原农业相关要素比较太湖平原东北平原人均耕地面积（公顷)0。

070。

31谷物年产（千克/公顷）124144916（1）根据材料一信息，比较两个工业区的工业区位条件的相同点和不同点。

（2）针对沪宁杭工业区在发展中的主要制约因素，近年来采取的措施有：A、建设西气东输工程；B、扩建大亚湾核电站；C、从国外大量进口铁矿资源;D、提高城乡居民收入；E、通过大力发展技术含量高、产品附加值高的高新技术产业；F、提高能源利用率.(3）从岛屿类型看,P岛为岛，随时间推移，其将首先与岸相连。

请指出该岛及其面积的扩大对上海市发展的影响。

（4)太湖平原的谷物单产远高于东北平原,主要原因是：。

（5）太湖平原自古就是国家的粮仓,通过京杭大运河向北方地区输送了大量的粮食，但近些年,长江三角洲地区的粮商却频频到东北调粮，南粮北上逐渐被北粮南下所取代。