云大附中七年级第一学期期末试卷2108-2019

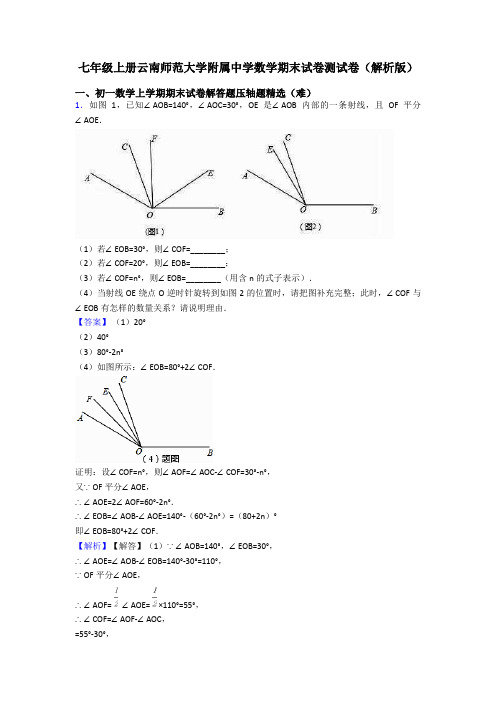
云南省昆明市2018-2019学年七年级上学期期末考试数学试题一、填空题（每小题3分，共18分）1．﹣5的相反数是．2．向东行驶3km记作+3km，向西行驶2km记作．3．世界文化遗产长城总长约为6700000m，将6700000用科学记数法表示应为．4．如果2x3m y4与﹣3x9y2n是同类项，那么m+n值为．5．一元一次方程4x＝18﹣2x的解为x＝．6．给定一列按规律排列的数：1，，，，，…则这列数的第10个数是．二、选择题（每小题4分，共32分）7．下列计算正确的是（）A．﹣5+3＝2 B．7x﹣4x＝3 C．﹣×＝1 D．﹣91÷7＝﹣13 8．当|a|＝﹣a时，则a是（）A．a≤0 B．a＜0 C．a≥0 D．a＞09．如图所示，已知O是直线AB上一点，∠1＝40°，OD平分∠BOC，则∠2的度数是（）A．20°B．25°C．30°D．70°10．在下图的四个立体图形中，从正面看是四边形的立体图形有（）A．1个B．2个C．3个D．4个11．下面去括号正确的是（）A．a﹣（b+1）＝a﹣b﹣1 B．2（x+3）＝2x+3C．x﹣（y﹣1）＝x﹣y﹣1 D．﹣3（m﹣n）＝﹣3m﹣3n12．已知2m﹣1＝2n，利用等式的性质比较m，n的大小是（）A．m＞n B．m＜n C．m＝n D．无法确定13．下列式子：，﹣2x，﹣abc，2a﹣m，0.56，，其中单项式有（）A．3个B．4个C．5个D．6个14．当x＝1时，代数式x﹣3的值是（）A．4 B．﹣3 C．﹣2 D．2三、解答题（本大题共9个小题，共70分）15．（8分）计算：（1）90°﹣17°27′（2）（﹣1）100×5+（﹣2）4÷416．（8分）化简下列各式：（1）5a﹣3b+a﹣2b（2）（8xy﹣x2+y2）﹣（x2﹣y2+8xy）17．（10分）解方程：（1）2（x+8）＝3（x﹣1）（2）﹣2＝18．（5分）先化简，再求值：﹣2（﹣x2+5+4x）﹣（2x2﹣4﹣5x），其中x＝﹣2．19．（5分）如图，点C是线段AB上的点，点D是线段BC的中点，若AB＝10，AC＝6，求CD的长．20．（8分）如图，OB是∠AOC的角平分线，OD是∠COE的角平分线，如果∠AOB＝40°，∠COE＝60°，则∠BOD的度数为多少度？21．（8分）某水库上周日的水位已达到警戒水位150米，本周内的水位变化情况如下：周一水位+0.4米，周二水位+1.3米，周三水位+0.5米，周四水位+1.2米，周五水位﹣0.5米，周六水位+0.4米，请问：（1）计算说明本周那一天水位最高，有多少米？（2）如果水位超过警戒水位0.6米就要放水，且放出后需保证水位在警戒水位，那么请说明本周应在那几天放水？（注：正号表示水位比前一天上升，负号表示水位比前一天下降）22．（8分）某项工程，甲单独做需20天完成，乙单独做需12天完成，甲、乙二人合做6天以后，再由乙继续完成，乙再做几天可以完成全部工程？23．（10分）某中学为了表彰在书法比赛中成绩突出的学生，购买了钢笔30支，毛笔45支，共用了1755元，其中每支毛笔比钢笔贵4元．（1）求钢笔和毛笔的单价各为多少元？（2）学校仍需要购买上面的两种笔共105支（每种笔的单价不变）．陈老师做完预算后，向财务处王老师说：“我这次买这两种笔需支领2447元．”王老师算了一下，说：“如果你用这些钱只买这两种笔，那么帐肯定算错了．”请你用学过的方程知识解释王老师为什么说他用这些钱只买这两种笔的帐算错了．参考答案一、填空题1．﹣5的相反数是 5 ．【分析】根据相反数的定义直接求得结果．解：﹣5的相反数是5．故答案为：5．【点评】本题主要考查了相反数的性质，只有符号不同的两个数互为相反数，0的相反数是0．2．向东行驶3km记作+3km，向西行驶2km记作﹣2km．【分析】根据正数和负数表示相反意义的量，向东记为正，可得答案．解：向东行驶3km，记作+3km，向西行驶2km记作﹣2km，故答案为﹣2km．【点评】本题考查了正数和负数，相反意义的量用正数和负数表示．3．世界文化遗产长城总长约为6700000m，将6700000用科学记数法表示应为 6.7×106．【分析】科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n 的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值＞1时，n是正数；当原数的绝对值＜1时，n是负数．解：6 700 000＝6.7×106，故答案为：6.7×106．【点评】此题考查科学记数法的表示方法．科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数，表示时关键要正确确定a的值以及n的值．4．如果2x3m y4与﹣3x9y2n是同类项，那么m+n值为 5 ．【分析】直接利用同类项的定义得出m，n的值，进而得出答案．解：∵2x3m y4与﹣3x9y2n是同类项，∴3m＝9，2n＝4，解得：m＝3，n＝2，∴m+n＝3+2＝5．故答案为：5．【点评】此题主要考查了同类项，正确掌握同类项的定义是解题关键．5．一元一次方程4x＝18﹣2x的解为x＝ 3 ．【分析】依次移项，合并同类项，系数化为1，即可得到答案．解：移项得：4x+2x＝18，合并同类项得：6x＝18，系数化为1得：x＝3，故答案为：3．【点评】本题考查了解一元一次方程，正确掌握解一元一次方程的方法是解题的关键．6．给定一列按规律排列的数：1，，，，，…则这列数的第10个数是．【分析】观察一系列等式，得到一般性规律，即可得到第10个数．解：根据题意得：一系列数的规律为（n为正整数），则这列数的第10个数为．故答案为：．【点评】此题考查了规律型：数字的变化类，弄清题中的规律是解本题的关键．二、选择题（本大题共8个小题，每小题4分，共32分）7．下列计算正确的是（）A．﹣5+3＝2 B．7x﹣4x＝3 C．﹣×＝1 D．﹣91÷7＝﹣13 【分析】直接利用有理数的混合运算法则以及合并同类项法则分别判断得出答案．解：A、﹣5+3＝﹣2，故原式计算错误；B、7x﹣4x＝3x，故原式计算错误；C、﹣×＝﹣，故原式计算错误；D、﹣91÷7＝﹣13，正确．故选：D．【点评】此题主要考查了有理数的混合运算以及合并同类项，正确掌握相关运算法则是解题关键．8．当|a|＝﹣a时，则a是（）A．a≤0 B．a＜0 C．a≥0 D．a＞0【分析】根据绝对值的含义和求法，可得负数和0的绝对值等于它的相反数，所以当|a|＝﹣a时，a≤0，据此判定即可．解：当|a|＝﹣a时，则a≤0．故选：A．【点评】此题主要考查了绝对值的含义和应用，要熟练掌握，解答此题的关键是要明确：①当a是正有理数时，a的绝对值是它本身a；②当a是负有理数时，a的绝对值是它的相反数﹣a；③当a是零时，a的绝对值是零．9．如图所示，已知O是直线AB上一点，∠1＝40°，OD平分∠BOC，则∠2的度数是（）A．20°B．25°C．30°D．70°【分析】先根据平角的定义求出∠COB的度数，再由OD平分∠BOC即可求出∠2的度数．解：∵∠1＝40°，∴∠COB＝180°﹣40°＝140°，∵OD平分∠BOC，∴∠2＝∠BOC＝×140°＝70°．故选：D．【点评】本题考查的是平角的定义及角平分线的定义，熟知以上知识是解答此题的关键．10．在下图的四个立体图形中，从正面看是四边形的立体图形有（）A．1个B．2个C．3个D．4个【分析】找到从正面看所得到的图形比较即可．解：正方体的正视图是四边形；球的正视图是圆；圆锥的正视图是等腰三角形；圆柱的正视图是四边形；是四边形的有两个．故选：B．【点评】本题考查了三视图的知识，正视图是从物体的正面看得到的视图．11．下面去括号正确的是（）A．a﹣（b+1）＝a﹣b﹣1 B．2（x+3）＝2x+3C．x﹣（y﹣1）＝x﹣y﹣1 D．﹣3（m﹣n）＝﹣3m﹣3n【分析】根据去括号的法则解答．解：A、a﹣（b+1）＝a﹣b﹣1，故本选项正确．B、2（x+3）＝2x+6，故本选项错误．C、x﹣（y﹣1）＝x﹣y+1，故本选项错误．D、﹣3（m﹣n）＝﹣3m+3n，故本选项错误．故选：A．【点评】此题考查去括号的方法：去括号时，运用乘法的分配律，先把括号前的数字与括号里各项相乘，再运用括号前是“+”，去括号后，括号里的各项都不改变符号；括号前是“﹣”，去括号后，括号里的各项都改变符号．顺序为先大后小．12．已知2m﹣1＝2n，利用等式的性质比较m，n的大小是（）A．m＞n B．m＜n C．m＝n D．无法确定【分析】等式两边同时除以2，减去n，加上，即可得到答案．解：等式两边同时除以2得：m﹣＝n，等式两边同时减去n得：m﹣n﹣＝0，等式两边同时加上得：m﹣n＝，即m﹣n＞0，即m＞n，故选：A．【点评】本题考查了等式的性质，正确掌握等式的性质是解题的关键．13．下列式子：，﹣2x ，﹣abc ，2a ﹣m ，0.56，，其中单项式有（ ）A ．3个B ．4个C ．5个D ．6个【分析】利用单项式的定义：数或字母的积组成的式子叫做单项式，单独的一个数或字母也是单项式，进而判断得出答案．解：，﹣2x ，﹣abc ，2a ﹣m ，0.56，，其中单项式有：，﹣2x ，﹣abc ，0.56，共4个． 故选：B ．【点评】此题主要考查了单项式，正确把握单项式的定义是解题关键． 14．当x ＝1时，代数式x ﹣3的值是（ ） A ．4B ．﹣3C ．﹣2D ．2【分析】将x ＝1代入x ﹣3，计算可得． 解：当x ＝1时，x ﹣3＝1﹣3＝﹣2， 故选：C ．【点评】本题主要考查代数式求值，题型简单总结以下三种：①已知条件不化简，所给代数式化简； ②已知条件化简，所给代数式不化简； ③已知条件和所给代数式都要化简．三、解答题（本大题共9个小题，共70分） 15．（8分）计算： （1）90°﹣17°27′（2）（﹣1）100×5+（﹣2）4÷4【分析】（1）根据1°＝60′，即1′＝60″进行解答；（2）有理数混合运算顺序：先算乘方，再算乘除，最后算加减；同级运算，应按从左到右的顺序进行计算．解：（1）90°﹣17°27′＝72°33′；（2）（﹣1）100×5+（﹣2）4÷4 ＝1×5+16÷4 ＝5+4 ＝9．【点评】考查了度分秒的换算，有理数的混合运算．属于基础题，熟记计算法则即可解答．16．（8分）化简下列各式：（1）5a﹣3b+a﹣2b（2）（8xy﹣x2+y2）﹣（x2﹣y2+8xy）【分析】（1）原式合并同类项即可得到结果；（2）原式去括号合并即可得到结果．解：（1）5a﹣3b+a﹣2b＝6a﹣5b；（2）（8xy﹣x2+y2）﹣（x2﹣y2+8xy）＝8xy﹣x2+y2﹣x2+y2﹣8xy＝﹣2x2+2y2．【点评】此题考查了整式的加减，熟练掌握运算法则是解本题的关键．17．（10分）解方程：（1）2（x+8）＝3（x﹣1）（2）﹣2＝【分析】（1）依次去括号，移项，合并同类项，系数化为1，即可得到答案，（2）依次去分母，去括号，移项，合并同类项，即可得到答案．解：（1）去括号得：2x+16＝3x﹣3，移项得：2x﹣3x＝﹣3﹣16，合并同类项得：﹣x＝﹣19，系数化为1得：x＝19，（2）去分母得：2（x+1）﹣8＝x，去括号得：2x+2﹣8＝x，移项得：2x﹣x＝8﹣2，合并同类项得：x＝6．【点评】本题考查了解一元一次方程，正确掌握解一元一次方程的方法是解题的关键．18．（5分）先化简，再求值：﹣2（﹣x2+5+4x）﹣（2x2﹣4﹣5x），其中x＝﹣2．【分析】先将原式去括号、合并同类项化简，再将x的值代入计算可得．解：﹣2（﹣x2+5+4x）﹣（ 2x2﹣4﹣5x）＝2x2﹣10﹣8x﹣2x2+4+5x＝﹣3x﹣6，当x＝﹣2时原式＝6﹣6＝0．【点评】本题主要考查整式的加减﹣化简求值，解题的关键是掌握去括号与合并同类项法则．19．（5分）如图，点C是线段AB上的点，点D是线段BC的中点，若AB＝10，AC＝6，求CD的长．【分析】根据题意，因为点D是线段BC的中点，所以BD＝DC＝BC，观察图形可知，故CD＝AB﹣AC﹣DB，即可得出结果．解：∵BC＝AB﹣AC＝4，∴DB＝2，∴CD＝DB＝2，∴CD的长为2．【点评】本题考查线段中点的意义及线段的和差运算，难度较小．20．（8分）如图，OB是∠AOC的角平分线，OD是∠COE的角平分线，如果∠AOB＝40°，∠COE＝60°，则∠BOD的度数为多少度？【分析】先根据O B是∠AOC的角平分线，OD是∠COE的角平分线，∠AOB＝40°，∠COE ＝60°求出∠BOC与∠COD的度数，再根据∠BOD＝∠BOC+∠COD即可得出结论．解：∵OB是∠AOC的角平分线，OD是∠COE的角平分线，∠AOB＝40°，∠COE＝60°，∴∠BOC＝∠AOB＝40°，∠COD＝∠COE＝×60°＝30°，∴∠BOD＝∠BOC+∠COD＝40°+30°＝70°．【点评】本题考查的是角平分线的定义和角的和差计算，熟知角平分线的定义是解答此题的关键．21．（8分）某水库上周日的水位已达到警戒水位150米，本周内的水位变化情况如下：周一水位+0.4米，周二水位+1.3米，周三水位+0.5米，周四水位+1.2米，周五水位﹣0.5米，周六水位+0.4米，请问：（1）计算说明本周那一天水位最高，有多少米？（2）如果水位超过警戒水位0.6米就要放水，且放出后需保证水位在警戒水位，那么请说明本周应在那几天放水？（注：正号表示水位比前一天上升，负号表示水位比前一天下降）【分析】（1）因为水位在持续上涨，所以周四最高，把前几个数相加在加上150米即可；（2）计算每一天的水位，然后再确定．解：（1）星期一水位：150+0.4＝150.4米，星期二水位：150.4+1.3＝151.7米，星期三水位：151.7+0.5＝152.2米，星期四水位：152.2+1.2＝153.4米，星期五水位：153.4﹣0.5＝152.9米，星期六水位：152.9+0.4＝153.3 m所以星期四的水位最高，为153.4米．（2）星期一水位150.4米，没有超过150.6米，所以不用放水，星期二水位151.7米，超过150.6米，故需要放水1.7米后变为150米．星期三水位150+0.5＝150.5米，不需要放水．星期四水位150.5+1.2＝151.7米，需要放水1.7米后变为150米．星期五水位150﹣0.5＝149.5米，不需要放水．星期六水位149.5+0.4＝149.9米，不需要放水．所以本周需在星期二，星期四放水．【点评】此题主要考查了正负数的意义，解题关键是理解“正”和“负”的相对性，明确什么是一对具有相反意义的量．在一对具有相反意义的量中，先规定其中一个为正，则另一个就用负表示．22．（8分）某项工程，甲单独做需20天完成，乙单独做需12天完成，甲、乙二人合做6天以后，再由乙继续完成，乙再做几天可以完成全部工程？【分析】根据甲单独做需20天完成，乙单独做需12天完成，可得出甲、乙每天完成的总工作量，再利用甲、乙两人合作6天后，再由乙继续完成，利用总工作量为1得出等式求出即可．解：设乙再做x天可以完成全部工程，由题意得：++＝1，解得：x＝≈3．答：乙再做3天可以完成全部工程．【点评】此题主要考查了一元一次方程的应用，关键是正确理解题意，分别表示出甲和乙的工作量，根据总工作量为1可得方程．23．（10分）某中学为了表彰在书法比赛中成绩突出的学生，购买了钢笔30支，毛笔45支，共用了1755元，其中每支毛笔比钢笔贵4元．（1）求钢笔和毛笔的单价各为多少元？（2）学校仍需要购买上面的两种笔共105支（每种笔的单价不变）．陈老师做完预算后，向财务处王老师说：“我这次买这两种笔需支领2447元．”王老师算了一下，说：“如果你用这些钱只买这两种笔，那么帐肯定算错了．”请你用学过的方程知识解释王老师为什么说他用这些钱只买这两种笔的帐算错了．【分析】（1）设钢笔的单价为x元，则毛笔的单价为（x+4）元，根据题意可得等量关系：30支钢笔的总价+45支毛笔的总价＝1755元，根据等量关系列出方程，再解即可．（2）设单价为21元的钢笔为y支，所以单价为25元的毛笔则为（105﹣y）支，根据题意可得等量关系：y支钢笔的总价+（105﹣y）支毛笔的总价＝2447元，列出方程，解出y的值不是整数，因此预算错误．解：（1）设钢笔的单价为x元，则毛笔的单价为（x+4）元．由题意得：30x+45（x+4）＝1755解得：x＝21则x+4＝25．答：钢笔的单价为21元，毛笔的单价为25元．（2）设单价为21元的钢笔为y支，所以单价为25元的毛笔则为（105﹣y）支．根据题意，得21y+25（105﹣y）＝2447．解得：y＝44.5 （不符合题意）．所以王老师肯定搞错了．。

2019学年云南省七年级上学期期末考试数学试卷【含答案及解析】姓名___________ 班级____________ 分数__________一、选择题1. 的相反数是（）A． B． C． D．2. 若数轴上点A表示的数是 -3, 则与点A相距4个单位长度的点表示的数是（）A．±4 B．±1 C．-7或1 D．-1或73. 下列关于单项式的说法中，正确的是（）A．系数是3，次数是2B．系数是，次数是2C．系数是，次数是3D．系数是，次数是34. 如图，BC=AB，D为AC的中点，，则AB的长是（）A、3cmB、4cmC、5cmD、6cm5. 下列去括号正确的是A．B．C．D．6. 如果2x2y3与x2yn+1是同类项，那么n的值是（）A．1 B．2 C．3 D．47. 下列结论中，不正确的是（）A．两点确定一条直线 B．两点之间，直线最短C．等角的余角相等 D．等角的补角相等8. 有理数的绝对值等于其本身的数有（）A．1个 B．2个 C．0个 D．无数个二、填空题9. 如果x=1时，代数式2ax3+3bx+4的值是5，那么x=﹣1时，代数式2ax3+3bx+4的值是．10. a平方的2倍与3的差，用代数式表示为________11. 武汉长江二桥是世界上第一座弧线形钢塔斜拉桥，该桥全长16800m，用科学记数法表示这个数为12. 如果，那么13. 如图是一个简单的数值运算程序，当输入的值为4时，则输出的结果为．14. 火车站、机场、邮局等场所都有为旅客提供打包服务的项目．现有一个长、宽、高分别为、、的箱子，按如图所示的方式打包，则打包带的长（不计接头处的长）至少应为__________ __15. 一个锐角是，它的余角是________度16. 观察下面单项式：，－2，根据你发现的规律，第6个式子是．三、解答题17. （3分）如图所示由五个小立方体构成的立体图形,请你分别画出从它的正面、左面、上面三个方向看所得到的平面图形．主视图（从正面看）左视图（从左面看）俯视图（从上面看）18. 计算（每小题4分，共16分）（1）（2）（3）（4）19. （6分）先化简，再求值：，其中20. 解方程（每小题4分，共8分）（1）（2）21. （6分）如图，∠AOB是直角，OD平分∠BOC，OE平分∠AOC，求∠EOD的度数．22. （6分）某工厂一周计划每日生产自行车100辆,由于工人实行轮休,每日上班人数不一定相等,实际每日生产量与计划量相比情况如下表（以计划量为标准,增加的车辆数记为正数,减少的车辆数记为负数）:23. 星期一二三四五六日增减/辆-1+3-2+4+7-5-10td24. （7分）甲、乙两站路程为360km,一列慢车从甲站开出，每小时行48km，一列快车从乙站开出，每小时行72km．（1）两车同时开出，相向而行，多少小时相遇？（2）若慢车先开出20分钟，快车再出发，两车同向而行，快车多少时间追上慢车？参考答案及解析第1题【答案】第2题【答案】第3题【答案】第4题【答案】第5题【答案】第6题【答案】第7题【答案】第8题【答案】第9题【答案】第10题【答案】第11题【答案】第12题【答案】第13题【答案】第14题【答案】第15题【答案】第16题【答案】第17题【答案】第18题【答案】第19题【答案】第20题【答案】第21题【答案】第22题【答案】第23题【答案】。

2018-2019第一学期七年级数学期末试卷及答案姓名__________ 分数______一、选择题（每小题3分，共30分） 1．一个数的相反数是2，这个数是（ ） A ．12 B ．12- C ．2 D ．-2 2．如果四个有理数的积是负数，那么其中负因数有（ ）个 A ．3 B ．1 C ．0或2 D ．1或33．火星和地球的距离约为34 000 000千米，用科学记数法表示34 000 000的结果是（ ） A ．0. 34×108 B ．3. 4×106 C ．34×106 D ．3. 4×107 4．关于x 的方程3x + 2m + 1 = x -3m -2的解为x = 0，则m 的值为（ ） A ．35-B ．15-C ．15D ．255．某种商品每件的进价为190元，按标价的九折销售时，利润率为15. 2%。

设这种商品的标价为每件x 元，依题意列方程正确的是（ ）A ．1900.91900.152x -=⨯B ．0.91900.152x =⨯C ．0.91901900.152x -=⨯D ．0.1521900.9x =⨯6．足球比赛计分规则是：胜一场得3分，平一场得1分，负一场得0分。

今年武汉黄鹤楼队经过26轮激战，以42分获“中超”联赛第五名，其中负6场，那么胜场数为（ ） A ．9 B ．10 C ．11 D ．127．下图是一个由6个相同的小立方体组成的几何体，从上面看得到的平面图形是（ ）A ．B ．C ．D ． 8．下面等式成立的是（ ）A ．83. 5°= 83°50′B ．37°12′36″=37. 48°C ．24°24′24″= 24. 44°D ．41. 25°= 41°15′9．某校为了解360名七年级学生体重情况，从中抽取了60名学生进行检测。

云大附中(一二一校区)2018-2019学年上学期期末考试七年级数学试卷(本试卷共三大题，27小题;考试时间120分钟;满分120分) 班级 姓名 学号 成绩一、选择题(本大题共10小题，共30分)1、从各个不同的方向观察如图所示的几何体，不可能看到的图形是( )(第1题图) A B C DA .A B.B C.C D.D2、某日，A 市的最高气温为12℃，最低气温为-2℃，A 市这天的最高气温比最低气温高( )A.10°CB.14°CC.-10°CD.-14°C3、单项式2357π-x y 的系数和次数分别是（ ） A.5,67- B. 357,π- C. 5,57- D. 557,π- 4、若()51113---+-b a x x x 是关于x 的四次三项式，那么ab 的值为（ ） A .4 B. -4 C.5 D.-55、下列等式的变形中，正确的有（ ）①由5x=3，得53=x ： ②由a=b ，得-a=-b; ③由=a b c c，得a=b;④由m=n ，得1=m n A.1个 B.2个 C.3个 D.4个6、“双十一”期间，某电商决定对网上销售的某种服装按成本价提高40%后标价，又以8折(即按标价的80%)优惠卖出，结果每件服装仍可获利21元，则这种服装每件的成本是( )A.160元B.165元C.170元D.175元7、下列命题中：①用两根钉子固定一根木条,体现数学事实是两点之间线段最短: ②射线AB 与射线BA 表示同一条射线: ③若AB=BC ，则B 为线段AC 的中点: ④两条直线被第三条直线所截，同位角相等：⑤在同一平面内,垂直于同一条直线的两条直线互相平行，真命题有( )A.1个B.2个C.3个D.4个8、如图，有A ，B ，C 三个地点，且AB ⊥BC ，从A 地测得B 地在A地的北偏东43°的方向上,那么从B 地测得C 地在B 地的( )A.南偏西43°B.南偏东43°C.北偏东47°D.北偏西479、a ，b 两数在数轴上表示如图所示，化简:-++b a a b 的结果是( ) A.-2b B .2a C.2b D.010、如图，下列条件: ①∠1=∠3; ②∠2+∠4=180°: ③∠4=∠5: ④∠2=∠3 ⑤∠6=∠2+∠3，其中能判断直线L 1∥L 2 （ ）A.5个B.4个C.3个D.2个二、填空题(本大题共10小题,共30分)11、港珠澳大桥于2018年10月24日正式通车,该工程总投资额为1269亿元,将1269亿用科学记数法表示为 元。

昆明市云大附中人教版七年级上册数学期末试卷及答案-百度文库一、选择题1A ．1B ．2C ．3D ．42．根据等式的性质，下列变形正确的是（ ）A ．若2a ＝3b ，则a ＝23b B ．若a ＝b ，则a +1＝b ﹣1 C ．若a ＝b ，则2﹣3a ＝2﹣3b D ．若23a b =，则2a ＝3b 3．下列选项中，运算正确的是（ ）A ．532x x -=B ．2ab ab ab -=C ．23a a a -+=-D ．235a b ab += 4．下列说法中正确的有（ ）A ．连接两点的线段叫做两点间的距离B ．过一点有且只有一条直线与已知直线垂直C ．对顶角相等D ．线段AB 的延长线与射线BA 是同一条射线5．某厂准备加工500个零件，在加工了100个零件后，引进了新机器，使得每天的工作效率是原来的两倍，结果共用了6天完成了任务,若设该厂原来每天加工ｘ个零件，则由题意可列出方程（）A ．10050062x x += B ．1005006x 2x += C ．10040062x x += D ．1004006x 2x+= 6．下列日常现象：①用两根钉子就可以把一根木条固定在墙上；②把弯曲的公路改直，就能够缩短路程；③体育课上，老师测量某个同学的跳远成绩；④建筑工人砌墙时，经常先在两端立桩拉线，然后沿着线砌墙．其中，可以用“两点确定一条直线”来解释的现象是( )A ．①④B ．②③C ．③D ．④7．下列四个数中最小的数是（ ）A ．﹣1B ．0C ．2D ．﹣（﹣1）8．下列变形不正确的是（ ）A ．若x ＝y ，则x+3＝y+3B ．若x ＝y ，则x ﹣3＝y ﹣3C ．若x ＝y ，则﹣3x ＝﹣3yD ．若x 2＝y 2，则x ＝y9．将方程212134x x -+=-去分母，得( ) A ．4(21)3(2)x x -=+ B ．4(21)12(2)x x -=-+ C ．(21)63(2)x x -=-+ D ．4(21)123(2)x x -=-+10．下列调查中，调查方式选择正确的是( )A ．为了了解1 000个灯泡的使用寿命，选择全面调查B ．为了了解某公园全年的游客流量， 选择抽样调查C ．为了了解生产的一批炮弹的杀伤半径，选择全面调查D ．为了了解一批袋装食品是否含有防腐剂，选择全面调查11．如图，C ，D 是线段AB 上两点，若CB ＝4cm ，DB ＝7cm ，且D 是AC 的中点，则AC 的长等于（ ）A ．3 cmB ．6 cmC ．11 cmD ．14 cm12．某商店出售两件衣服，每件卖了200元，其中一件赚了25%，而另一件赔了20%．那么商店在这次交易中( )A ．亏了10元钱B ．赚了10钱C ．赚了20元钱D ．亏了20元钱二、填空题13．将一根木条固定在墙上只用了两个钉子，这样做的依据是_______________.14．已知x=5是方程ax ﹣8=20+a 的解，则a= ________15．将0.09493用四舍五入法取近似值精确到百分位，其结果是_____．16．若212-m y x 与5x 3y 2n 是同类项，则m +n ＝_____． 17．﹣30×（1223-+45）＝_____． 18．如图，点B 在线段AC 上，且AB ＝5，BC ＝3，点D ，E 分别是AC ，AB 的中点，则线段ED 的长度为_____．19．如图，是七(2)班全体学生的体有测试情况扇形统计图.若达到优秀的有25人，则不合格的学生有____人.20．比较大小：﹣（﹣9）_____﹣（+9）填“＞”，“＜”，或”＝”符号）21．如图，∠AOB＝∠COD＝90°，∠AOD＝140°，则∠BOC＝_______．22．我国高速公路发展迅速，据报道，到目前为止，全国高速公路总里程约为118000千米，用科学记数法表示为_____千米．23．已知7635a ∠=︒'，则a ∠的补角为______°______′.24．若-3x 2m+6y 3与2x 4y n 是同类项，则m+n=______．三、压轴题25．数轴上A 、B 两点对应的数分别是﹣4、12，线段CE 在数轴上运动，点C 在点E 的左边，且CE ＝8，点F 是AE 的中点．（1）如图1，当线段CE 运动到点C 、E 均在A 、B 之间时，若CF ＝1，则AB ＝ ，AC ＝ ，BE ＝ ；（2）当线段CE 运动到点A 在C 、E 之间时,①设AF 长为x ，用含x 的代数式表示BE ＝ （结果需化简．．．．．）； ②求BE 与CF 的数量关系；（3）当点C 运动到数轴上表示数﹣14的位置时，动点P 从点E 出发，以每秒3个单位长度的速度向右运动，抵达B 后，立即以原来一半速度返回，同时点Q 从A 出发，以每秒2个单位长度的速度向终点B 运动，设它们运动的时间为t 秒（t ≤8），求t 为何值时，P 、Q 两点间的距离为1个单位长度．26．如图，已知数轴上点A 表示的数为8，B 是数轴上位于点A 左侧一点，且AB =22，动点P 从A 点出发，以每秒5个单位长度的速度沿数轴向左匀速运动，设运动时间为t （t ＞0）秒．（1）出数轴上点B 表示的数 ；点P 表示的数 （用含t 的代数式表示）（2）动点Q 从点B 出发，以每秒3个单位长度的速度沿数轴向右匀速运动，若点P 、Q 同时出发，问多少秒时P 、Q 之间的距离恰好等于2？（3）动点Q 从点B 出发，以每秒3个单位长度的速度沿数轴向左匀速运动，若点P 、Q 同时出发，问点P 运动多少秒时追上点Q ？（4）若M 为AP 的中点，N 为BP 的中点，在点P 运动的过程中，线段MN 的长度是否发生变化？若变化，请说明理由，若不变，请你画出图形，并求出线段MN 的长．27．对于数轴上的点P，Q，给出如下定义：若点P到点Q的距离为d(d≥0)，则称d为点P 到点Q的d追随值，记作d[PQ]．例如，在数轴上点P表示的数是2，点Q表示的数是5，则点P到点Q的d追随值为d[PQ]=3．问题解决：(1)点M，N都在数轴上，点M表示的数是1，且点N到点M的d追随值d[MN]=a(a≥0)，则点N表示的数是_____(用含a的代数式表示)；(2)如图，点C表示的数是1，在数轴上有两个动点A，B都沿着正方向同时移动，其中A点的速度为每秒3个单位，B点的速度为每秒1个单位，点A从点C出发，点B表示的数是b，设运动时间为t(t>0)．①当b=4时，问t为何值时，点A到点B的d追随值d[AB]=2；②若0<t≤3时，点A到点B的d追随值d[AB]≤6，求b的取值范围．28．如图，已知数轴上点A表示的数为8，B是数轴上位于点A左侧一点，且AB=20，动点P从A点出发，以每秒5个单位长度的速度沿数轴向左匀速运动，设运动时间为t（t＞0）秒．（1）写出数轴上点B表示的数______；点P表示的数______（用含t的代数式表示）（2）动点Q从点B出发，以每秒3个单位长度的速度沿数轴向右匀速运动，若点P、Q同时出发，问多少秒时P、Q之间的距离恰好等于2？（3）动点Q从点B出发，以每秒3个单位长度的速度沿数轴向左匀速到家动，若点P、Q 同时出发，问点P运动多少秒时追上Q？（4）若M为AP的中点，N为BP的中点，在点P运动的过程中，线段MN的长度是否发生变化？若变化，请说明理由，若不变，请你画出图形，并求出线段MN的长．29．已知：如图数轴上两点A、B所对应的数分别为-3、1，点P在数轴上从点A出发以每秒钟2个单位长度的速度向右运动，点Q在数轴上从点B出发以每秒钟1个单位长度的速度向左运动，设点P的运动时间为t秒．（1）若点P和点Q同时出发，求点P和点Q相遇时的位置所对应的数；（2）若点P比点Q迟1秒钟出发，问点P出发几秒后，点P和点Q刚好相距1个单位长度；（3）在（2）的条件下，当点P和点Q刚好相距1个单位长度时，数轴上是否存在一个点C，使其到点A、点P和点Q这三点的距离和最小，若存在，直接写出点C所对应的数，若不存在，试说明理由．30．在数轴上，图中点A表示－36，点B表示44，动点P、Q分别从A、B两点同时出发，相向而行，动点P、Q的运动速度比之是3∶2（速度单位：1个单位长度/秒）．12秒后，动点P到达原点O，动点Q到达点C，设运动的时间为t（t＞0）秒．（1）求OC的长；（2）经过t秒钟，P、Q两点之间相距5个单位长度，求t的值；（3）若动点P到达B点后，以原速度立即返回，当P点运动至原点时，动点Q是否到达A点，若到达，求提前到达了多少时间，若未能到达，说明理由．31．数轴上线段的长度可以用线段端点表示的数进行减法运算得到，例如：如图①，若点A，B在数轴上分别对应的数为a，b(a<b)，则AB的长度可以表示为AB=b－a．请你用以上知识解决问题：如图②，一个点从数轴上的原点开始，先向左移动2个单位长度到达A点，再向右移动3个单位长度到达B点，然后向右移动5个单位长度到达C点．（1）请你在图②的数轴上表示出A，B，C三点的位置．（2）若点A以每秒1个单位长度的速度向左移动，同时，点B和点C分别以每秒2个单位长度和3个单位长度的速度向右移动，设移动时间为t秒．①当t=2时，求AB和AC的长度；②试探究：在移动过程中，3AC－4AB的值是否随着时间t的变化而改变？若变化，请说明理由；若不变，请求其值．32．已知：如图，点A、B分别是∠MON的边OM、ON上两点，OC平分∠MON，在∠CON的内部取一点P（点A、P、B三点不在同一直线上），连接PA、PB．（1）探索∠APB与∠MON、∠PAO、∠PBO之间的数量关系，并证明你的结论；（2）设∠OAP=x°，∠OBP=y°，若∠APB的平分线PQ交OC于点Q，求∠OQP的度数（用含有x、y的代数式表示）．【参考答案】***试卷处理标记，请不要删除一、选择题1．B解析：B【解析】【分析】根据算术平方根的概念可得出答案.【详解】解：根据题意可得：，故答案为：B.【点睛】本题考查算术平方根的概念,解题关键在于对其概念的理解.2．C解析：C【解析】【分析】利用等式的性质对每个式子进行变形即可找出答案．【详解】解：A 、根据等式性质2，2a ＝3b 两边同时除以2得a ＝32b ，原变形错误，故此选项不符合题意；B 、根据等式性质1，等式两边都加上1，即可得到a+＝b+1，原变形错误，故此选项不符合题意；C 、根据等式性质1和2，等式两边同时除以﹣3且加上2应得2﹣3a ＝2﹣3b ，原变形正确，故此选项符合题意；D 、根据等式性质2，等式两边同时乘以6，3a ＝2b ，原变形错误，故此选项不符合题意． 故选：C ．【点睛】本题主要考查等式的性质．解题的关键是掌握等式的性质．运用等式性质1必须注意等式两边所加上的（或减去的）必须是同一个数或整式；运用等式性质2必须注意等式两边所乘的（或除的）数或式子不为0，才能保证所得的结果仍是等式． 3．B解析：B【解析】【分析】根据整式的加减法法则即可得答案.【详解】A.5x-3x=2x ，故该选项计算错误，不符合题意，B.2ab ab ab-=，计算正确，符合题意，C.-2a+3a=a，故该选项计算错误，不符合题意，D.2a与3b不是同类项，不能合并，故该选项计算错误，不符合题意，故选：B.【点睛】本题考查整式的加减，熟练掌握合并同类项法则是解题关键.4．C解析：C【解析】【分析】分别利用直线的性质以及射线的定义和垂线定义分析得出即可．【详解】A．连接两点的线段的长度叫做两点间的距离，错误；B．在同一平面内，过一点有且只有一条直线与已知直线垂直，错误；C．对顶角相等，正确；D．线段AB的延长线与射线BA不是同一条射线，错误．故选C．【点睛】本题考查了直线的性质以及射线的定义和垂线的性质，正确把握相关定义和性质是解题的关键．5．D解析：D【解析】【分析】根据共用6天完成任务，等量关系为：用老机器加工100个零件用的时间+用新机器加工400套用的时间=6即可列出方程．【详解】设该厂原来每天加工x个零件，根据题意得：1004006 x2x+=故选：D．【点睛】此题考查了由实际问题抽象出分式方程，分析题意，找到关键描述语，找到合适的等量关系是解决问题的关键．6．A解析：A【解析】【分析】根据点到直线的距离，直线的性质，线段的性质，可得答案．①用两根钉子就可以把一根木条固定在墙上，利用了两点确定一条直线，故①正确；②把弯曲的公路改直，就能够缩短路程，利用“两点之间线段最短”，故②错误；③体育课上，老师测量某个同学的跳远成绩，利用了点到直线的距离，故③错误；④建筑工人砌墙时，经常先在两端立桩拉线，然后沿着线砌墙，利用了两点确定一条直线，故④正确．故选A．【点睛】本题考查了线段的性质，熟记性质并能灵活应用是解答本题的关键．7．A解析：A【解析】【分析】首先根据有理数大小比较的方法，把所给的四个数从大到小排列即可．【详解】解：﹣（﹣1）＝1，∴﹣1＜0＜﹣（﹣1）＜2，故选：A．【点睛】此题主要考查了有理数大小比较的方法，要熟练掌握正数都大于0，负数都小于0，正数大于一切负数．两个负数比较大小，绝对值大的反而小．8．D解析：D【解析】【分析】根据等式的两边同时加上（或减去）同一个数（或字母），等式仍成立；等式的两边同时乘以（或除以）同一个不为0数（或字母），等式仍成立．【详解】解：A、两边都加上3，等式仍成立，故本选项不符合题意．B、两边都减去3，等式仍成立，故本选项不符合题意．C、两边都乘以﹣3，等式仍成立，故本选项不符合题意．D、两边开方，则x＝y或x＝﹣y，故本选项符合题意．故选：D．【点睛】本题主要考查了等式的基本性质．解题的关键是掌握等式的基本性质，等式的两边同时加上（或减去）同一个数（或字母），等式仍成立；等式的两边同时乘以（或除以）同一个不为0数（或字母），等式仍成立．9．D解析：D【分析】方程两边同乘12即可得答案．【详解】方程212134x x-+=-两边同时乘12得：4(21)123(2)x x-=-+故选：D．【点睛】本题考查一元一次方程去分母，找出分母的最小公倍数是解题的关键，注意不要漏乘．10．B解析：B【解析】选项A、C、D，了解1000个灯泡的使用寿命，了解生产的一批炮弹的杀伤半径，了解一批袋装食品是否含有防腐剂，都是具有破坏性的调查，无法进行普查，不适于全面调查，适用于抽样调查．选项B，了解某公园全年的游客流量，工作量大，时间长，需要用抽样调查．故选B．11．B解析：B【解析】【分析】由CB＝4cm，DB＝7cm求得CD=3cm，再根据D是AC的中点即可求得AC的长【详解】∵C，D是线段AB上两点，CB＝4cm，DB＝7cm，∴CD＝DB﹣BC＝7﹣4＝3（cm），∵D是AC的中点，∴AC＝2CD＝2×3＝6（cm）．故选：B．【点睛】此题考察线段的运算，根据图形确定线段之间的数量关系即可正确解答.12．A解析：A【解析】设一件的进件为x元，另一件的进价为y元，则x（1+25%）=200，解得，x=160，y（1-20%）=200，解得，y=250，∴（200-160）+（200-250）=-10（元），∴这家商店这次交易亏了10元.二、填空题13．两点确定一条直线．【解析】将一根木条固定在墙上只用了两个钉子，他这样做的依据是：两点确定一条直线．故答案为两点确定一条直线．解析：两点确定一条直线．【解析】将一根木条固定在墙上只用了两个钉子，他这样做的依据是：两点确定一条直线．故答案为两点确定一条直线．14．7【解析】试题分析：使方程左右两边相等的未知数的值是该方程的解．将方程的解代入方程可得关于a的一元一次方程，从而可求出a的值．解：把x=5代入方程ax﹣8=20+a得：5a﹣8=20+a，解析：7【解析】试题分析：使方程左右两边相等的未知数的值是该方程的解．将方程的解代入方程可得关于a的一元一次方程，从而可求出a的值．解：把x=5代入方程ax﹣8=20+a得：5a﹣8=20+a，解得：a=7．故答案为7．考点：方程的解．15．09．【解析】【分析】把千分位上的数字4进行四舍五入即可．【详解】解：将0.09493用四舍五入法取近似值精确到百分位，其结果是0.09．故答案为0.09．【点睛】本题考查了近似数和解析：09．【解析】【分析】把千分位上的数字4进行四舍五入即可．【详解】解：将0.09493用四舍五入法取近似值精确到百分位，其结果是0.09．故答案为0.09．【点睛】本题考查了近似数和有效数字：近似数与精确数的接近程度，可以用精确度表示．一般有，精确到哪一位，保留几个有效数字等说法．16．4【解析】【分析】根据同类项的定义（所含字母相同，相同字母的指数相同）列出方程，求出n，m的值，再代入代数式计算即可.【详解】解：根据题意得：2n＝2，m＝3，解得：n＝1，m＝3，则解析：4【解析】【分析】根据同类项的定义（所含字母相同，相同字母的指数相同）列出方程，求出n，m的值，再代入代数式计算即可.【详解】解：根据题意得：2n＝2，m＝3，解得：n＝1，m＝3，则m+n＝4．故答案是：4．【点睛】本题考查了利用同类项的定义求字母的值，熟练掌握同类项的定义是解答本题的关键，所含字母相同，并且相同字母的指数也相同的项，叫做同类项，根据相同字母的指数相同列方程（或方程组）求解即可.17．﹣19．【解析】【分析】根据乘法分配律简便计算即可求解．【详解】解：﹣30×（+）＝﹣30×+（﹣30）×（）+（﹣30）× ＝﹣15+20﹣24＝﹣19．故答案为：﹣19．【点睛解析：﹣19．【解析】【分析】根据乘法分配律简便计算即可求解．【详解】解：﹣30×（1223-+45）＝﹣30×12+（﹣30）×（23-）+（﹣30）×45＝﹣15+20﹣24＝﹣19．故答案为：﹣19．【点睛】本题考查了有理数的混合运算，熟练掌握运算法则和运算顺序是正确解题的关键. 18．5【解析】【分析】首先求出AC的长度是多少，根据点D是AC的中点，求出AD的长度是多少；然后求出AE的长度，即可求出线段ED的长度为多少．【详解】解：∵AB＝5，BC＝3，∴AC＝5+3解析：5【解析】【分析】首先求出AC的长度是多少，根据点D是AC的中点，求出AD的长度是多少；然后求出AE的长度，即可求出线段ED的长度为多少．【详解】解：∵AB＝5，BC＝3，∴AC＝5+3＝8；∵点D是AC的中点，∴AD＝8÷2＝4；∵点E是AB的中点，∴AE＝5÷2＝2.5，∴ED＝AD﹣AE＝4﹣2.5＝1.5．故答案为：1.5．【点睛】此题主要考查了两点间的距离，以及线段的中点的含义和应用，要熟练掌握．19．5【解析】【分析】根据达到优秀的人数和所占百分比求出总人数，然后用总人数乘以不合格所占的百分比即可.【详解】解：∵学生总人数=25÷50%=50（人），∴不合格的学生人数=50×（1-5解析：5【解析】【分析】根据达到优秀的人数和所占百分比求出总人数，然后用总人数乘以不合格所占的百分比即可.【详解】解：∵学生总人数=25÷50%=50（人），∴不合格的学生人数=50×（1-50%-40%）=5（人），故答案为：5.【点睛】本题考查了扇形统计图，熟知扇形统计图中各数据所表示的意义是解题关键.20．＞【解析】【分析】根据有理数的大小比较的法则负数都小于0，正数都大于0，正数大于一切负数进行比较即可．【详解】解：，，．故答案为：【点睛】本题考查了多重符号化简和有理数的大小比较，解析：＞【解析】【分析】根据有理数的大小比较的法则负数都小于0，正数都大于0，正数大于一切负数进行比较即可．【详解】解：(9)9--=，(9)9-+=-，(9)(9)∴-->-+．故答案为：>【点睛】本题考查了多重符号化简和有理数的大小比较，掌握有理数的大小比较法则是解题的关键，理数的大小比较法则是负数都小于0，正数都大于0，正数大于一切负数，两个负数比较大小，其绝对值大的反而小．21．40°【解析】解：由角的和差，得：∠AOC=∠AOD -∠COD=140°-90°=50°．由余角的性质，得：∠COB=90°-∠AOC=90°-50°=40°．故答案为：40°．解析：40°【解析】解：由角的和差，得：∠AOC =∠AOD -∠COD =140°-90°=50°．由余角的性质，得：∠COB =90°-∠AOC =90°-50°=40°．故答案为：40°．22．18×105【解析】【分析】科学记数法的表示形式为a×10n 的形式，其中1≤|a|<10，n 为整数．确定n 的值时，要看把原数变成a 时，小数点移动了多少位，n 的绝对值与小数点移动的位数相同．当原解析：18×105【解析】【分析】科学记数法的表示形式为a×10n 的形式，其中1≤|a|<10，n 为整数．确定n 的值时，要看把原数变成a 时，小数点移动了多少位，n 的绝对值与小数点移动的位数相同．当原数绝对值>1时，n 是正数；当原数的绝对值<1时，n 是负数．【详解】解:118000=1.18×105，故答案为1.18×105．23．25【解析】【分析】根据补角的概念，两个角加起来等于180°，就是互为补角，即可求解.【详解】的补角为故答案为103；25.【点睛】此题主要考查补角的求解，熟练掌握，即可解题解析：25【解析】【分析】根据补角的概念，两个角加起来等于180°，就是互为补角，即可求解.【详解】a ∠的补角为180762313550'='︒-︒︒故答案为103；25.【点睛】此题主要考查补角的求解，熟练掌握，即可解题.24．2【解析】【分析】根据同类项的定义列出方程，求出n ，m 的值，再代入代数式计算即可．【详解】∵单项式-3x2m+6y3与2x4yn 是同类项，∴2m+6=4，n=3，∴m=-1，∴m+n解析：2【解析】【分析】根据同类项的定义列出方程，求出n ，m 的值，再代入代数式计算即可．【详解】∵单项式-3x 2m+6y 3与2x 4y n 是同类项，∴2m+6=4，n=3，∴m=-1，∴m+n=-1+3=2.故答案为：2.【点睛】本题考查同类项的定义. 所含字母相同，并且相同字母的指数相等的项叫做同类项．三、压轴题25．（1）16,6,2；（2）①162x -②2BE CF =；（3）t=1或3或487或527 【解析】【分析】(1)由数轴上A 、B 两点对应的数分別是-4、12，可得AB 的长;由CE ＝8，CF ＝1，可得EF 的长，由点F 是AE 的中点，可得AF 的长，用AB 的长减去2倍的EF 的长即为BE 的长；(2)设AF ＝FE ＝x ，则CF ＝8-x ，用含x 的式子表示出BE ，即可得出答案(3)分①当0＜t ≤6时； ②当6＜t ≤8时，两种情况讨论计算即可得解【详解】（1）数轴上A 、B 两点对应的数分别是-4、12，∴AB=16，∵CE=8，CF=1，∴EF=7，∵点F 是AE 的中点，∴AF=EF=7，,∴AC=AF ﹣CF=6，BE=AB ﹣AE=16﹣7×2=2，故答案为16，6，2；(2)∵点F 是AE 的中点，∴AF=EF ，设AF=EF=x,∴CF=8﹣x ，∴BE=16﹣2x=2（8﹣x ），∴BE=2CF.故答案为①162x -②2BE CF =；(3) ①当0＜t ≤6时，P 对应数：-6+3t ，Q 对应数-4+2t ， =4t t =2t =1PQ ﹣＋2﹣（﹣6＋3）﹣，解得：t=1或3；②当6＜t ≤8时，P 对应数()33126t 22t ---＝21 ， Q 对应数-4+2t ， 37=4t =t 2=12t PQ -﹣＋2﹣（）25﹣21， 解得：48t=7或527； 故答案为t=1或3或487或527. 【点睛】 本题考查了一元一次方程在数轴上的动点问题中的应用，根据题意正确列式，是解题的关健26．（1）﹣14，8﹣5t ；（2）2.5或3秒时P 、Q 之间的距离恰好等于2；（3）点P 运动11秒时追上点Q ；（4）线段MN 的长度不发生变化，其值为11，见解析.【解析】【分析】（1）根据已知可得B点表示的数为8﹣22；点P表示的数为8﹣5t；（2）设t秒时P、Q 之间的距离恰好等于2．分①点P、Q相遇之前和②点P、Q相遇之后两种情况求t值即可；（3）设点P运动x秒时，在点C处追上点Q，则AC=5x，BC=3x，根据AC﹣BC=AB，列出方程求解即可；（3）分①当点P在点A、B两点之间运动时，②当点P运动到点B的左侧时，利用中点的定义和线段的和差求出MN的长即可．【详解】（1）∵点A表示的数为8，B在A点左边，AB=22，∴点B表示的数是8﹣22=﹣14，∵动点P从点A出发，以每秒5个单位长度的速度沿数轴向左匀速运动，设运动时间为t （t＞0）秒，∴点P表示的数是8﹣5t．故答案为：﹣14，8﹣5t；（2）若点P、Q同时出发，设t秒时P、Q之间的距离恰好等于2．分两种情况：①点P、Q相遇之前，由题意得3t+2+5t=22，解得t=2.5；②点P、Q相遇之后，由题意得3t﹣2+5t=22，解得t=3．答：若点P、Q同时出发，2.5或3秒时P、Q之间的距离恰好等于2；（3）设点P运动x秒时，在点C处追上点Q，则AC=5x，BC=3x，∵AC﹣BC=AB，∴5x﹣3x=22，解得：x=11，∴点P运动11秒时追上点Q；（4）线段MN的长度不发生变化，都等于11；理由如下：①当点P在点A、B两点之间运动时：MN=MP+NP=12AP+12BP=12（AP+BP）=12AB=12×22=11；②当点P运动到点B的左侧时：MN=MP﹣NP=12AP﹣12BP=12（AP﹣BP）=12AB=11，∴线段MN的长度不发生变化，其值为11．【点睛】本题考查了数轴一元一次方程的应用，用到的知识点是数轴上两点之间的距离，关键是根据题意画出图形，注意分两种情况进行讨论．27．(1)1＋a或1－a；(2)12或52；(3)1≤b≤7.【解析】【分析】(1)根据d追随值的定义，分点N在点M左侧和点N在点M右侧两种情况，直接写出答案即可；(2)①分点A在点B左侧和点A在点B右侧两种情况，类比行程问题中的追及问题，根据“追及时间=追及路程÷速度差”计算即可；②【详解】解：(1)点N在点M右侧时，点N表示的数是1+a；点N在点M左侧时，点N表示的数是1-a；(2)①b=4时，AB相距3个单位，当点A在点B左侧时，t=(3-2)÷(3-1)=12，当点A在点B右侧时，t=(3+2)÷(3-1)=52；②当点B在点A左侧或重合时，即d≤1时，随着时间的增大，d追随值会越来越大，∵0<t≤3，点A到点B的d追随值d[AB]≤6，∴1-d+3×(3-1)≤6，解得d≥1，∴d=1，当点B在点A右侧时，即d>1时，在AB重合之前，随着时间的增大，d追随值会越来越小，∵点A到点B的d追随值d[AB]≤6，∴d≤7∴1<d≤7，综合两种情况，d的取值范围是1≤d≤7.故答案为(1)1＋a或1－a；(2)①12或52；②1≤b≤7.【点睛】本题考查了数轴上两点之间的距离和动点问题.28．（1）-12,8-5t；（2）94或114；（3）10；（4）MN的长度不变，值为10.【解析】【分析】(1)根据已知可得B点表示的数为8﹣20；点P表示的数为8﹣5t；(2)运动时间为t秒，分点P、Q相遇前相距2，相遇后相距2两种情况列方程进行求解即可；(3)设点P运动x秒时追上Q，根据P、Q之间相距20，列方程求解即可；(4)分①当点P在点A、B两点之间运动时，②当点P运动到点B的左侧时，利用中点的定义和线段的和差求出MN的长即可．【详解】(1)∵点A表示的数为8，B在A点左边，AB=20，∴点B表示的数是8﹣20=﹣12，∵动点P从点A出发，以每秒5个单位长度的速度沿数轴向左匀速运动，设运动时间为t(t＞0)秒，∴点P表示的数是8﹣5t，故答案为﹣12，8﹣5t；(2)若点P、Q同时出发，设t秒时P、Q之间的距离恰好等于2；分两种情况：①点P、Q相遇之前，由题意得3t+2+5t=20，解得t=94；②点P、Q相遇之后，由题意得3t﹣2+5t=20，解得t=11 4，答：若点P、Q同时出发，94或114秒时P、Q之间的距离恰好等于2；(3)如图，设点P运动x秒时，在点C处追上点Q，则AC=5x，BC=3x，∵AC﹣BC=AB，∴5x﹣3x=20，解得：x=10，∴点P运动10秒时追上点Q；(4)线段MN的长度不发生变化，都等于10；理由如下：①当点P在点A、B两点之间运动时：MN=MP+NP=12AP+12BP=12(AP+BP)=12AB=10，②当点P运动到点B的左侧时：MN=MP﹣NP=12AP﹣12BP=12(AP﹣BP)=12AB=10，∴线段MN的长度不发生变化，其值为10．【点睛】本题考查了数轴上的动点问题，一元一次方程的应用，用到的知识点是数轴上两点之间的距离，关键是根据题意画出图形，注意分两种情况进行讨论．29．（1）13-；（2）P 出发23秒或43秒；(3)见解析. 【解析】【分析】(1)由题意可知运动t 秒时P 点表示的数为-3+2t ，Q 点表示的数为1-t ，若P 、Q 相遇，则P 、Q 两点表示的数相等，由此可得关于t 的方程，解方程即可求得答案；(2)由点P 比点Q 迟1秒钟出发，则点Q 运动了(t+1)秒，分相遇前相距1个单位长度与相遇后相距1个单位长度两种情况分别求解即可得；(3)设点C 表示的数为a ，根据两点间的距离进行求解即可得.【详解】(1)由题意可知运动t 秒时P 点表示的数为-5+t ，Q 点表示的数为10-2t ；若P ，Q 两点相遇，则有-3+2t=1-t ，解得：t=43， ∴413233-+⨯=-， ∴点P 和点Q 相遇时的位置所对应的数为13-；(2)∵点P 比点Q 迟1秒钟出发，∴点Q 运动了(t+1)秒，若点P 和点Q 在相遇前相距1个单位长度，则()2t 1t 141+⨯+=-， 解得：2t 3=； 若点P 和点Q 在相遇后相距1个单位长度，则2t+1×(t+1) =4+1， 解得：4t 3=， 综合上述，当P 出发23秒或43秒时，P 和点Q 相距1个单位长度； (3)①若点P 和点Q 在相遇前相距1个单位长度，此时点P 表示的数为-3+2×23=-53，Q 点表示的数为1-(1+23)=-23， 设此时数轴上存在-个点C ，点C 表示的数为a ，由题意得 AC+PC+QC=|a+3|+|a+53|+|a+23|，要使|a+3|+|a+53|+|a+23|最小，当点C与P重合时，即a=-53时，点C到点A、点P和点Q这三点的距离和最小；②若点P和点Q在相遇后相距1个单位长度，此时点P表示的数为-3+2×43=-13，Q点表示的数为1-(1+43)=-43，此时满足条件的点C即为Q点，所表示的数为43 -，综上所述，点C所表示的数分别为-53和-43.【点睛】本题考查了数轴上的动点问题，一元一次方程的应用，数轴上两点间的距离，正确理解数轴上两点间的距离，从中找到等量关系列出方程是解题的关键.本题也考查了分类讨论思想.30．（1）20；（2）t=15s或17s （3）4 3 s.【解析】【分析】（1）设P、Q速度分别为3m、2m，根据12秒后，动点P到达原点O列方程，求出P、Q 的速度，由此即可得到结论．（2）分两种情况讨论：①当A、B在相遇前且相距5个单位长度时；②当A、B在相遇后且相距5个单位长度时；列方程，求解即可．（3）算出P运动到B再到原点时，所用的时间，再算出Q从B到A所需的时间，比较即可得出结论．【详解】（1）设P、Q速度分别为3m、2m，根据题意得：12×3m=36，解得：m=1，∴P、Q速度分别为3、2，∴BC=12×2=24，∴OC=OB－BC=44－24=20．（2）当A、B在相遇前且相距5个单位长度时：3t＋2t＋5=44＋36，5t=75，∴t=15（s）；当A、B在相遇后且相距5个单位长度时：3t＋2t－5=44＋36，5t=85，∴t=17（s）．综上所述：t=15s或17s．（3）P运动到原点时，t=3644443++=1243s，此时QB=2×1243=2483＞44+38=80，∴Q点已到达A点，∴Q点已到达A点的时间为：3644804022+==（s），故提前的时间为：1243－40=43（s）．【点睛】本题考查了一元一次方程的应用-行程问题以及数轴上的动点问题．解题的关键是找出等量。

2018-2019学年度第一学期期末教学质量检测七年级数学试卷一、选择题：每小题只有一个选项符合题意，本大题共6小题，每小题3分，满分18分．1．（3分）|﹣3|的相反数是（）A．B．﹣C．3D．﹣32．（3分）过度包装既浪费资源又污染环境．据测算，如果全国每年减少10%的过度包装纸用量，那么可减排二氧化碳3120000吨，把数3120000用科学记数法表示为（）A．3.12×105B．3.12×106C．31.2×105D．0.312×1073．（3分）下列说法中，正确的是（）A．若AP=PB，则点P是线段AB的中点B．射线比直线短C．连接两点的线段叫做两点间的距离D．过六边形的一个顶点作对角线，可以将这个六边形分成4个三角形4．（3分）如图，下列各图形中的三个数之间均具有相同的规律．根据此规律，图形中M与m、n的关系是（）A．M=mn B．M=m（n+1）C．M=mn+1D．M=n（m+1）5．（3分）如图，把一张长方形的纸片沿着EF折叠，点C、D分别落在M、N的位置，且∠MFB=∠MFE．则∠MFB=（）A．30°B．36°C．45°D．72°6．（3分）过正方体中有公共顶点的三条棱的中点切出一个平面，形成如图几何体，其正确展开图正确的为（）A．B．C．D．二、填空题，本大题共6小题，每小题3分，共18分．7．（3分）一天早晨的气温是﹣2℃，半夜又下降了1℃，则半夜的气温是℃．8．（3分）请你写出一个只含有字母m、n，且它的系数为﹣2、次数为3的单项式．9．（3分）已知∠α的补角是它的3倍，则∠α=．10．（3分）已知x2+3x=1，则多项式3x2+9x﹣1的值是．11．（3分）如图所示，点A、点B、点C分别表示有理数a、b、c，O为原点，化简：|a﹣c|﹣|b﹣c|=．12．（3分）用小立方块搭成的几何体从正面和上面看的视图如图，这个几何体中小立方块的个数可以是．三、解答题（本大题共5小题，每小题6分，共30分）13．（6分）计算：（1）点A、B、C在同一条直线上，点C在线段AB上，若AB=4，BC=1，求AC；（2）已知|x|=3，y2=4，且x＜y＜0，那么求x+y的值．14．（6分）计算．﹣14﹣（1﹣0.5）× [3﹣（﹣3）2]．15．（6分）根据下列语句，画出图形．如图：已知：四点A、B、C、D．①画直线AB；②画射线AC、BD，相交于点O．16．（6分）根据下面给出的数轴，解答下面的问题：（1）请你根据图中A、B两点的位置，分别写出它们所表示的有理数A：B：；（2）观察数轴，与点A的距离为4的点表示的数是：；（3）若将数轴折叠，使得A点与﹣3表示的点重合，则B点与数表示的点重合．17．（6分）先化简，再求值：﹣a2b+（3ab2﹣a2b）﹣2（2ab2﹣a2b），其中a=﹣1，b=﹣2．四、解答题（本大题共3小题，每小题8分，共24分）18．（8分）为了了解学生参加体育活动的情况，学校对学生进行随机抽样调查，其中一个问题是“你平均每天参加体育活动的时间是多少”，共有4个选项：A、1.5小时以上；B、1～1.5小时；C、0.5～1小时；D、0.5小时以下．图1、2是根据调查结果绘制的两幅不完整的统计图，请你根据统计图提供的信息，解答以下问题：（1）本次一共调查了多少名学生？（2）在图1中将选项B的部分补充完整；（3）若该校有3000名学生，你估计全校可能有多少名学生平均每天参加体育活动的时间在0.5小时以下？19．（8分）已知关于x的方程2（x+1）﹣m=﹣的解比方程5（x﹣1）﹣1=4（x﹣1）+1的解大2．（1）求第二个方程的解；（2）求m的值．20．（8分）“囧”（jiong）是最近时期网络流行语，像一个人脸郁闷的神情．如图所示，一张边长为20的正方形的纸片，剪去两个一样的小直角三角形和一个长方形得到一个“囧”字图案（阴影部分）．设剪去的小长方形长和宽分别为x、y，剪去的两个小直角三角形的两直角边长也分别为x、y．（1）用含有x、y的代数式表示图中“囧”的面积；（2）若|x﹣6|+（y﹣3）2=0时，求此时“囧”的面积．五、解答题（本大题共2小题，每小题9分，共18分）21．（9分）一个车队共有n（n为正整数）辆小轿车，正以每小时36千米的速度在一条笔直的街道上匀速行驶，行驶时车与车的间隔均为5.4米，甲停在路边等人，他发现该车队从第一辆车的车头到最后一辆的车尾经过自己身边共用了20秒的时间，假设每辆车的车长均为4.87米．（1）求n的值；（2）若乙在街道一侧的人行道上与车队同向而行，速度为v米/秒，当第一辆车的车头到最后一辆车的车尾经过他身边共用了40秒，求v的值．22．（9分）已知数轴上两点A、B对应的数分别是6，﹣8，M、N、P为数轴上三个动点，点M 从A点出发速度为每秒2个单位，点N从点B出发速度为M点的3倍，点P从原点出发速度为每秒1个单位．（1）若点M向右运动，同时点N向左运动，求多长时间点M与点N相距54个单位？（2）若点M、N、P同时都向右运动，求多长时间点P到点M，N的距离相等？六、解答题（本大题共1小题，共12分）23．（12分）【问题提出】已知∠AOB=70°，∠AOD=∠AOC，∠BOD=3∠BOC（∠BOC＜45°），求∠BOC的度数．【问题思考】聪明的小明用分类讨论的方法解决．（1）当射线OC在∠AOB的内部时，①若射线OD在∠AOC内部，如图1，可求∠BOC的度数，解答过程如下：设∠BOC=α，∴∠BOD=3∠BOC=3α，∴∠COD=∠BOD﹣∠BOC=2α，∴∠AOD=∠AOC，∴∠AOD=∠COD=2α，∴∠AOB=∠AOD+∠BOD=2α+3α=5α=70°，∴α=14°，∴∠BOC=14°问：当射线OC在∠AOB的内部时，②若射线OD在∠AOB外部，如图2，请你求出∠BOC的度数；【问题延伸】（2）当射线OC在∠AOB的外部时，请你画出图形，并求∠BOC的度数．【问题解决】综上所述：∠BOC的度数分别是．参考答案与试题解析一、选择题：每小题只有一个选项符合题意，本大题共6小题，每小题3分，满分18分．1．（3分）|﹣3|的相反数是（）A．B．﹣C．3D．﹣3【分析】先根据绝对值的意义得到|﹣3|=3，然后根据相反数的定义求解．【解答】解：|﹣3|=3，3的相反数为﹣3，所以|﹣3|的相反数为﹣3．故选：D．【点评】本题考查了绝对值：当a＞0时，|a|=a；当a=0，|a|=0；当a＜0时，|a|=﹣a．也考查了相反数．2．（3分）过度包装既浪费资源又污染环境．据测算，如果全国每年减少10%的过度包装纸用量，那么可减排二氧化碳3120000吨，把数3120000用科学记数法表示为（）A．3.12×105B．3.12×106C．31.2×105D．0.312×107【分析】科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值＞1时，n是正数；当原数的绝对值＜1时，n是负数．【解答】解：将3120000用科学记数法表示为：3.12×106．故选：B．【点评】此题考查了科学记数法的表示方法．科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数，表示时关键要正确确定a的值以及n的值．3．（3分）下列说法中，正确的是（）A．若AP=PB，则点P是线段AB的中点B．射线比直线短C．连接两点的线段叫做两点间的距离D．过六边形的一个顶点作对角线，可以将这个六边形分成4个三角形【分析】根据线段中点的性质可得AP=PB=AB，根据射线和直线的性质可得B错误；根据两点之间的距离定义可得C错误；n边形从一个顶点出发可引出（n﹣3）条对角线，分成（n﹣2）个三角形．【解答】解：A、若AP=PB=AB，则点P是线段AB的中点，故原题说法错误；B、射线比直线短，说法错误；C、连接两点的线段长度叫做两点间的距离，故原题说法错误；D、过六边形的一个顶点作对角线，可以将这个六边形分成4个三角形说法正确；故选：D．【点评】此题主要考查了直线、射线、多边形、以及两点之间的距离，关键是注意连接两点的线段长度叫做两点间的距离．4．（3分）如图，下列各图形中的三个数之间均具有相同的规律．根据此规律，图形中M与m、n的关系是（）A．M=mn B．M=m（n+1）C．M=mn+1D．M=n（m+1）【分析】根据给定图形中三个数之间的关系找出规律“右下圆圈内的数=上方圆圈内的数×（左下圆圈内的数+1）”，由此即可得出结论．【解答】解：∵1×（2+1）=3，3×（4+1）=15，5×（6+1）=35，∴右下圆圈内的数=上方圆圈内的数×（左下圆圈内的数+1），∴M=m（n+1）．故选：B．【点评】本题考查了规律型中数字的变化类，根据给定图形中三个数之间的关系找出变化规律“右下圆圈内的数=上方圆圈内的数×（左下圆圈内的数+1）”是解题的关键．5．（3分）如图，把一张长方形的纸片沿着EF折叠，点C、D分别落在M、N的位置，且∠MFB=∠MFE．则∠MFB=（）A．30°B．36°C．45°D．72°【分析】由折叠的性质可得：∠MFE=∠EFC，又由∠MFB=∠MFE，可设∠MFB=x°，然后根据平角的定义，即可得方程：x+2x+2x=180，解此方程即可求得答案．【解答】解：由折叠的性质可得：∠MFE=∠EFC，∵∠MFB=∠MFE，设∠MFB=x°，则∠MFE=∠EFC=2x°，∵∠MFB+∠MFE+∠EFC=180°，∴x+2x+2x=180，解得：x=36°，∴∠MFB=36°．故选：B．【点评】此题考查了折叠的性质与平角的定义．此题比较简单，解题的关键是注意方程思想与数形结合思想的应用．6．（3分）过正方体中有公共顶点的三条棱的中点切出一个平面，形成如图几何体，其正确展开图正确的为（）A．B．C．D．【分析】由平面图形的折叠及立体图形的表面展开图的特点解题．【解答】解：选项A、C、D折叠后都不符合题意，只有选项B折叠后两个剪去三角形与另一个剪去的三角形交于一个顶点，•与正方体三个剪去三角形交于一个顶点符合．故选：B．【点评】考查了截一个几何体和几何体的展开图．解决此类问题，要充分考虑带有各种符号的面的特点及位置．二、填空题，本大题共6小题，每小题3分，共18分．7．（3分）一天早晨的气温是﹣2℃，半夜又下降了1℃，则半夜的气温是﹣3℃．【分析】直接利用有理数的加减运算法则计算得出答案．【解答】解：由题意可得：半夜的气温是：﹣2﹣1=﹣3（℃）．故答案为：﹣3．【点评】此题主要考查了有理数的加减运算，正确掌握运算法则是解题关键．8．（3分）请你写出一个只含有字母m、n，且它的系数为﹣2、次数为3的单项式﹣2m2n（答案不唯一）．【分析】直接利用单项式的定义分析得出答案．【解答】解：∵写一个只含有字母m、n，且它的系数为﹣2、次数为3的单项式，∴可以为：﹣2m2n（答案不唯一）．故答案为：﹣2m2n（答案不唯一）．【点评】此题主要考查了单项式，正确把握单项式的次数与系数是解题关键．9．（3分）已知∠α的补角是它的3倍，则∠α=45°．【分析】先表示出这个角的补角，然后再依据∠α的补角是它的3倍列出方程，从而可求得∠α的度数．【解答】解：∠α的补角是180°﹣α．根据题意得：180°﹣∠α=3∠α．解得：∠α=45°．故答案为：45°．【点评】本题主要考查的是余角和补角的定义，依据题意列出方程是解题的关键．10．（3分）已知x2+3x=1，则多项式3x2+9x﹣1的值是2．【分析】原式前两项提取3变形后，将已知等式代入计算即可求出值．【解答】解：∵x2+3x=1，∴原式=3（x2+3x）﹣1=3﹣1=2，故答案为：2【点评】此题考查了代数式求值，利用了整体代入的思想，熟练掌握运算法则是解本题的关键．11．（3分）如图所示，点A、点B、点C分别表示有理数a、b、c，O为原点，化简：|a﹣c|﹣|b﹣c|=2c﹣a﹣b．【分析】根据各点在数轴上的位置判断出a、b、c的符号及绝对值的大小，再去绝对值符号，合并同类项即可．【解答】解：∵由图可知，a＜c＜0＜b， ∴a﹣c＜0，b﹣c＞0， ∴原式=c﹣a﹣（b﹣c）=c﹣a﹣b+c=2c﹣a﹣b． 故答案为：2c﹣a﹣b． 【点评】 本题考查的是整式的加减， 熟知整式的加减实质上就是合并同类项是解答此题的关键． 12． （3 分）用小立方块搭成的几何体从正面和上面看的视图如图，这个几何体中小立方块的个 数可以是 8、9、10 ．【分析】从俯视图中可以看出最底层小正方体的个数及形状，从主视图和左视图可以看出每一 层小正方体的层数和个数，从而算出总的个数． 【解答】解：从俯视图可以看出，下面的一层有 6 个，由主视图可以知道在中间一列的一个正 方体上面可以放 2 个或在一个上放 2 个，另一个上放 1 或 2 个； 所以小立方块的个数可以是 6+2=8 个，6+2+1=9 个，6+2+2=10 个． 故答案为：8、9、10． 【点评】考查学生对三视图掌握程度和灵活运用能力，同时也体现了对空间想象能力方面的考 查．如果掌握口诀“俯视图打地基，正视图疯狂盖，左视图拆违章”就更容易得到答案．三、解答题（本大题共 5 小题，每小题 6 分，共 30 分） 13． （6 分）计算： （1）点 A、B、C 在同一条直线上，点 C 在线段 AB 上，若 AB=4，BC=1，求 AC； （2）已知|x|=3，y2=4，且 x＜y＜0，那么求 x+y 的值． 【分析】 （1）根据线段的和差，可得答案； （2）根据非负数的性质，可得 x，y，根据有理数的加法，可得答案． 【解答】解： （1）如图 由线段的和差，得 AC=AB﹣BC=4﹣1=3； （2）由|x|=3，y2=4，且 x＜y＜0，得 x=﹣3，y=﹣2． ，x+y=（﹣3）+（﹣2）=﹣5． 【点评】本题考查了两点间的距离，利用线段的和差是解题关键． 14． （6 分）计算． ﹣14﹣（1﹣0.5）× [3﹣（﹣3）2]．【分析】先乘方，再乘除，最后算加减即可． 【解答】解：﹣14﹣（1﹣0.5）× =﹣1﹣ × ×（﹣6） =﹣1+1 =0 【点评】此题考查了有理数的混合运算，有理数的混合运算首先弄清运算顺序，先乘方，再乘 除，最后算加减，有括号先算括号里边的，同级运算从左到右依次进行计算，然后利用各种 运算法则进行计算，有时可以利用运算律来简化运算． 15． （6 分）根据下列语句，画出图形．如图：已知：四点 A、B、C、D． ①画直线 AB； ②画射线 AC、BD，相交于点 O． [3﹣（﹣3）2]【分析】根据直线、射线的定义画图即可． 【解答】解：如图所示【点评】此题主要考查了简单作图，解答此题需要熟练掌握直线、射线、线段的性质，认真作 图解答即可． 16． （6 分）根据下面给出的数轴，解答下面的问题：（1）请你根据图中 A、B 两点的位置，分别写出它们所表示的有理数 A： 1 （2）观察数轴，与点 A 的距离为 4 的点表示的数是： 5 或﹣3 ； 0.5B： ﹣2.5；（3）若将数轴折叠，使得 A 点与﹣3 表示的点重合，则 B 点与数 【分析】 （1）直接根据数轴上 AB 两点的位置即可得出结论； （2）根据 A 点所表示的数即可得出结论； （3）根据中点坐标公式即可得出结论．表示的点重合．【解答】解： （1）由数轴上 AB 两点的位置可知，A 点表示 1，B 点表示﹣2.5． 故答案为：1，﹣2.5；（2）∵A 点表示 1， ∴与点 A 的距离为 4 的点表示的数是 5 或﹣3． 故答案为：5 或﹣3；（3）∵A 点与﹣3 表示的点重合， ∴其中点= =﹣1，∵点 B 表示﹣2.5， ∴与 B 点重合的数=﹣2+2.5=0.5． 故答案为：0.5． 【点评】本题考查的是数轴，熟知数轴上各点与实数是一一对应关系是解答此题的关键． 17． （6 分）先化简，再求值：﹣a2b+（3ab2﹣a2b）﹣2（2ab2﹣a2b） ，其中 a=﹣1，b=﹣2． 【分析】先去括号、合并同类项将原式化简，再将 a、b 的值代入计算可得． 【解答】解：原式=﹣a2b+3ab2﹣a2b﹣4ab2+2a2b =﹣ab2， 当 a=﹣1、b=﹣2 时， 原式=﹣（﹣1）×（﹣2）2 =1×4 =4． 【点评】本题主要考查整式的化简求值，解题的关键是熟练掌握整式的混合运算顺序和法则．四、解答题（本大题共 3 小题，每小题 8 分，共 24 分）18． （8 分）为了了解学生参加体育活动的情况，学校对学生进行随机抽样调查，其中一个问题 是“你平均每天参加体育活动的时间是多少”，共有 4 个选项：A、1.5 小时以上；B、1～1.5 小 时；C、0.5～1 小时；D、0.5 小时以下．图 1、2 是根据调查结果绘制的两幅不完整的统计图， 请你根据统计图提供的信息，解答以下问题： （1）本次一共调查了多少名学生？ （2）在图 1 中将选项 B 的部分补充完整； （3）若该校有 3000 名学生，你估计全校可能有多少名学生平均每天参加体育活动的时间在 0.5小时以下？【分析】 （1）读图可得：A 类有 60 人，占 30%即可求得总人数； （2）计算可得：“B”是 100 人，据此补全条形图； （3）用样本估计总体，若该校有 3000 名学生，则学校有 3000×5%=150 人平均每天参加体育锻 炼在 0.5 小时以下． 【解答】解： （1）读图可得：A 类有 60 人，占 30%；则本次一共调查了 60÷30%=200 人；本次 一共调查了 200 位学生；（2）“B”有 200﹣60﹣30﹣10=100 人，画图正确；（3）用样本估计总体，每天参加体育锻炼在 0.5 小时以下占 5%；则 3000×5%=150， 学校有 150 人平均每天参加体育锻炼在 0.5 小时以下．【点评】本题考查的是条形统计图和扇形统计图的综合运用．读懂统计图，从不同的统计图中 得到必要的信息是解决问题的关键．条形统计图能清楚地表示出每个项目的数据；扇形统计 图直接反映部分占总体的百分比大小． 19． （8 分）已知关于 x 的方程 2（x+1）﹣m=﹣ 解大 2． （1）求第二个方程的解； （2）求 m 的值． 【分析】 （1）首先去括号，移项、合并同类项可得 x 的值； （2）根据（1）中 x 的值可得方程 2（x+1）﹣m=﹣ 得关于 m 的方程，再解即可． 【解答】解： （1）5（x﹣1）﹣1=4（x﹣1）+1， 5x﹣5﹣1=4x﹣4+1， 5x﹣4x=﹣4+1+1+5， x=3； （2）由题意得：方程 2（x+1）﹣m=﹣ 把 x=5 代入方程 2（x+1）﹣m=﹣ 2（5+1）﹣m=﹣ 12﹣m=﹣ m=22． 【点评】此题主要考查了一元一次方程的解，关键是掌握使一元一次方程左右两边相等的未知 数的值叫做一元一次方程的解．把方程的解代入原方程，等式左右两边相等． 20． （8 分）“囧”（jiong）是最近时期网络流行语，像一个人脸郁闷的神情．如图所示，一张边 长为 20 的正方形的纸片， 剪去两个一样的小直角三角形和一个长方形得到一个“囧”字图案 （阴 ， ， 得： 的解为 x=3+2=5， 的解为 x=3+2=5，然后把 x 的值代入可 的解比方程 5（x﹣1）﹣1=4（x﹣1）+1 的影部分） ．设剪去的小长方形长和宽分别为 x、y，剪去的两个小直角三角形的两直角边长也 分别为 x、y． （1）用含有 x、y 的代数式表示图中“囧”的面积； （2）若|x﹣6|+（y﹣3）2=0 时，求此时“囧”的面积．【分析】 （1）根据图形和题意可以用代数式表示出图中“囧”的面积； （2）根据|x﹣6|+（y﹣3）2=0，可以求得 x、y 的值，然后代入（1）中的代数式即可解答本题． 【解答】解： （1）由图可得， 图中“囧”的面积是：20×20﹣ 即图中“囧”的面积是 400﹣2xy； （2）∵|x﹣6|+（y﹣3）2=0 ∴x﹣6=0，y﹣3=0， 解得，x=6，y=3， ∴400﹣2xy=400﹣2×6×3=400﹣36=364， 即|x﹣6|+（y﹣3）2=0 时，此时“囧”的面积是 364． 【点评】本题考查列代数式、非负数的性质，解答本题的关键是明确题意，写出相应的代数式， 求出相应的代数式的值． ﹣xy=400﹣xy﹣xy=400﹣2xy，五、解答题（本大题共 2 小题，每小题 9 分，共 18 分） 21． （9 分）一个车队共有 n（n 为正整数）辆小轿车，正以每小时 36 千米的速度在一条笔直的 街道上匀速行驶，行驶时车与车的间隔均为 5.4 米，甲停在路边等人，他发现该车队从第一 辆车的车头到最后一辆的车尾经过自己身边共用了 20 秒的时间， 假设每辆车的车长均为 4.87 米． （1）求 n 的值； （2）若乙在街道一侧的人行道上与车队同向而行，速度为 v 米/秒，当第一辆车的车头到最后一 辆车的车尾经过他身边共用了 40 秒，求 v 的值． 【分析】 （1）首先统一单位，由题意得等量关系：n（n 为正整数）辆小轿车的总长+（n﹣1）个每辆车之间的车距=20 秒×车的行驶速度，根据等量关系列出方程，再解即可； （2）计算出车对的总长度，再利用总路程为 200m 得出等式求出答案． 【解答】解：36 千米/小时=10 米/秒， 根据题意得，4.87n+5.4（n﹣1）=20×10， 解得，n=20；（2）车队总长度为：20×4.87+5.4×19=200（米） ， 根据题意得， （10﹣v）×40=200， 解得，v=5， 即：v 的值为 5 米/秒． 【点评】此题主要考查了一元一次方程的应用，利用路程、速度、时间之间的关系得出方程是 解题关键． 22． （9 分）已知数轴上两点 A、B 对应的数分别是 6，﹣8，M、N、P 为数轴上三个动点，点 M 从 A 点出发速度为每秒 2 个单位，点 N 从点 B 出发速度为 M 点的 3 倍，点 P 从原点出发速 度为每秒 1 个单位． （1）若点 M 向右运动，同时点 N 向左运动，求多长时间点 M 与点 N 相距 54 个单位？ （2）若点 M、N、P 同时都向右运动，求多长时间点 P 到点 M，N 的距离相等？【分析】 （1） 设经过 x 秒点 M 与点 N 相距 54 个单位， 由点 M 从 A 点出发速度为每秒 2 个单位， 点 N 从点 B 出发速度为 M 点的 3 倍，得出 2x+6x+14=54 求出即可； （2）首先设经过 t 秒点 P 到点 M，N 的距离相等，得出（2t+6）﹣t=（6t﹣8）﹣t 或（2t+6）﹣ t=t﹣（6t﹣8） ，进而求出即可． 【解答】解： （1）设经过 x 秒点 M 与点 N 相距 54 个单位． 依题意可列方程为：2x+6x+14=54， 解方程，得 x=5． 答：经过 5 秒点 M 与点 N 相距 54 个单位． （算术方法对应给分）（2）设经过 t 秒点 P 到点 M，N 的距离相等． （2t+6）﹣t=（6t﹣8）﹣t 或（2t+6）﹣t=t﹣（6t﹣8） ， t+6=5t﹣8 或 t+6=8﹣5tt= 或 t= ， 答：经过 或 秒点 P 到点 M，N 的距离相等． 【点评】此题主要考查了一元一次方程的应用，根据已知点运动速度得出以及距离之间的关系 得出等式是解题关键．六、解答题（本大题共 1 小题，共 12 分） 23． （12 分） 【问题提出】已知∠AOB=70°，∠AOD= ∠AOC，∠BOD=3∠BOC（∠BOC＜45°） ， 求∠BOC 的度数． 【问题思考】聪明的小明用分类讨论的方法解决． （1）当射线 OC 在∠AOB 的内部时，①若射线 OD 在∠AOC 内部，如图 1，可求∠BOC 的度数， 解答过程如下： 设∠BOC=α， ∴∠BOD=3∠BOC=3α， ∴∠COD=∠BOD﹣∠BOC=2α， ∴∠AOD= ∠ AOC， ∴∠AOD=∠COD=2α，∴∠AOB=∠AOD+∠BOD=2α+3α=5α=70°，∴α=14°，∴∠ BOC=14° 问：当射线 OC 在∠AOB 的内部时，②若射线 OD 在∠AOB 外部，如图 2，请你求出∠BOC 的度 数； 【问题延伸】 （2）当射线 OC 在∠AOB 的外部时，请你画出图形，并求∠BOC 的度数． 【问题解决】综上所述：∠BOC 的度数分别是 14°，30°，10°，42° ．【分析】 （1）②由已知条件得出∠COD、∠AOD、∠AOB 与∠BOC 的关系，求出∠BOC 的度数； （2）分类讨论，根据∠AOD、∠BOD．∠AOB 与∠BOC 的关系，得出∠BOC 的度数． 【解答】解： （1）②设∠BOC=α，则∠BOD=3α，②若射线 OD 在∠AOB 外部， 如图 2：∠COD=∠BOD﹣∠BOC=2α， ∵∠AOD= ∠AOC，∴∠AOD= ∠COD=， = =70°，∴∠AOB=∠BOD﹣∠AOD=3α﹣ ∴α=30°． ∴∠BOC=30°；（2）当射线 OC 在∠AOB 外部时，根据题意，此时射线 OC 靠近射线 OB， ∵∠BOC＜45°，∠AOD= ∠AOC， ∴射线 OD 的位置也只有两种可能； ①若射线 OD 在∠AOB 内部，如图 3 所示， 则∠COD=∠BOC+∠COD=4α， ∴∠AOB=∠BOD+∠AOD=3α+4α=7α=70°， ∴α=10°， ∴∠BOC=10°； ②若射线 OD 在∠AOB 外部，如图 4， 则∠COD=∠BOC+∠BOD=4α， ∵∠AOD= ∠AOC， ∴∠AOD= ∠COD= α， ∴∠AOB=∠BOD﹣∠AOD=3α﹣ ∴α=42°， ∴∠BOC=42°； 综上所述：∠BOC 的度数分别是 14°，30°，10°，42°． = =70°，【点评】根据 OC、OD 的不同位置分类讨论∠BOC 的计算方法；分类讨论是关键．。

七年级期末试卷一、积累与运用1、【答案】D【解析】本体考察学生对字音的掌握情况，要求学生平时积累字词，注意读准字音。

本题中，各选项错误读音修改为：A.确凿（záo）狭隘（ài）蹒跚（pán）, 共三个；B.怂恿（sǒng）C. 蝉蜕（tuì）干涸（hé）蜷伏（quán），共三个；D.殉职（xùn）坍塌（tān）嗔怪（chēn）莽莽榛榛（zhēn）,共四个。

故本题选D。

2、【答案】C【解析】本题考察学生的词语积累和对形近字的辨析。

要求学生平时学习中注意形近字辨析，注意其用法的不同。

本题中用法错误的字修改为：A.琢磨B.漠不关心美不胜收 D.云霄故本题选C。

3、【答案】A【解析】本题考察学生对常见语病类型的分析。

要求学生掌握常用句式，了解常见的语病类型，语序不当、搭配不当、成分残缺、成分赘余、结构混乱、语意不明、不合逻辑等。

本题中，B选项中，结构混乱，主语被淹没，应把“由于”或“使”去掉一个。

C 选项中，成分赘余，把“造成的”去掉。

D选项中，语意不明，把“没有”去掉。

A选项无语病，故选A。

4、【答案】B【解析】本题考察学生文学常识的积累，要求学生平时多了解古今中外的文学名著。

本题中，B选项《伊索寓言》，作者并非古罗马作家。

《伊索寓言》相传为公元前六世纪被释放的古希腊奴隶伊索所著的寓言集，并加入印度、阿拉伯及基督教故事，共357篇。

故选B。

5、【答案】C【解析】本题考察考生语言逻辑思维能力，较难。

解答此类题目注意上文直接语言的衔接，例如本段文字第一句是"苏州地处水乡"，那么紧接着的一句必然要和苏州"水"有关，所以后面一句为②，②又提到"因水就势造园"，后面接的也应当和"造园"有关，只有⑤符合，前两个顺序也就确定下。

6、【答案】（1）山岛竦峙（2）我寄愁心与明月（3）终古高云簇此城，秋风吹散马蹄声。

云大附中（一二一校区）2018-2019学年上学期期中考试七年级数学试卷（本试卷共3大题，28小题；考试时间120分钟，满分120分） 班级：_________姓名：_________学号：____________成绩：___________一、填空题（共10小题，每小题3分，满分30分）1. 52-的倒数是_______. 2. 甲地的气温是15-℃，乙地的气温比甲地高8℃，则乙地的气温是___________℃.3. 比较大小：.,,_____14.3-”连接）π（用“<=>- 4. 若==+++-）（则b a b a 20182,0|2|)3(_____________.5. 如果._______41055=-=+=a a ax x 的解，那么是方程6. 若.________24-1342=--+n m yxyx n m 为同类项，则与7. 一个多项式加上22-2-+x x得到12-x ，z 则这个多项式是__________.8. 若多项式y x 322-的值为6，则多项式10642+-y x的值为___________.9. 把一批图书分给某班学生阅读，如果每人分3本，则剩余20本，如果每人分4本，则还缺25本，这个班有_____________________名学生. 10. 已知b a b a a b+<==则且,,4,3||2的值为________________.二、选择题（共10小题，每小题只有一个正确选项，每小题3分，满分30分）11. 《九章算术》中注有“今两算得失相反，要令正负以名之”，意思是：今有两数若其意义相反，则分别叫做正数与负数，若气温为零上10℃记作10+℃，则3-℃表示气温为（ ） A. 零上3℃ B.零下3℃ C.零上7℃ D.零下7℃ 12. 我国倡导的“一带一路”建设将促进我国与世界一些国家的互利合作，根据规划“一带一路”地区覆盖总人口为4400000000人，这个数用科学计数法表示为（ ） A. 10844⨯ B.1084.4⨯ C.1094.4⨯D.10104.4⨯13. 下列说法正确的是（ ）A. bc bc a a22-31与不是同类项 B.32n m 不是整式 B. 单项式yx 23-的系数是1- D.y xx y 2253+-是二次三项式14. 下列去括号正确的是（ ）A.c b a c b a +-=+-+)(B.c b a c b a +-=+--)(C.c b a c b a -+=-+2)(2D.c b a c b a 22)(2--=-- 15.下列利用等式的性质错误的是（ ） A.由c b c a c b a =≠=得到且,0, B.由b a b==得到,22a C.由bc ac b ==得到,a D.由522-5,--==b b a 得到 16.在|2-|-2--416-2-2），（，，）（中，负数的个数是（ ） A.1个 B.2个 C.3个 D.4个17.下列说法中，正确的是（ ）A.最小的负有理数是1-B.近似数10430.2⨯精确到百分位C.0的相反数、倒数均是0D.如果a 的绝对值是a ，那么a 是正数或者零 18.三角形一条边长,3+a 第二条边长12-a ，第三条边长)42-a （，那么这个三角形的周长为（ ）A.95+aB.92+aC.65-aD.10+a 19.实数d c b a 、、、在数轴上的点如图所示，则正确的结论是（ ）A. 0>+c aB.0<abC.4->aD.||||b a >20. 如图，有四个大小相同的小长方形和两个大小相同的大长方形按照如图位置摆放，按图中所示尺寸，则小长方形的长与宽的差是（ ）A.a b 23-B.2b a -C.3b a -D.43ba -三．解答题（共8题，满分60分，解答时必须写出必要的计算过程、推理或文字说明） 21.计算：（每小题3分，共12分） （1）15-7-18--12）（）（+ （2））（）（）（52-321-313-⨯÷ （2））（）（48-121-4361-⨯+ （4））（）（52-11-21325--22⨯÷22.解方程：（每小题4分，共8分）（1）x x 23273-=+ （2）1233+=-x x23.化简：（每小题3分，共6分）（1）3357+-+-y x y x （2）)42(3)322222y x x y x y y x--+（24.先化简，再求值：（5分）21,2,5)]4(22[322222=-=-+---b a a a b a b b b a b a 其中.25.（5分）一张桌子可坐6人，按下列方式将桌子拼在一起.①2张桌子拼在一起可坐_____人，4张桌子拼在一起可坐_______人，n 张桌子拼在一起可坐（_____________）人.（3分）②一家餐厅有40张这样的长方形桌子，按照上图方式每5张拼成一张大桌子，则40张桌子可拼成8张大桌子，共可坐__________人.（1分）③若在②中，改成8张桌子拼成一张大桌子，则共可坐________人.（1分）26. （6分）某摩托车厂家本周计划每天生产250辆摩托车，由于工厂实行轮休，每天上班人数不一定相等，实际每天生产与计划生产情况如下表（增加的辆数记为正数，减少的记为（2）本周总产量与计划相比，是增产还是减产？具体数量是多少？（2分） （3）产量最多的一天比产量最少的一天多生产多少辆？（2分）27. （8分）科技人员研制出采摘水果的单人便携式采摘机，已知雇一个工手工采摘每小时可采摘水果10公斤，一个雇工操作该采摘机每小时可摘水果35公斤，雇工每天工作8小时. （1）一个雇工手工采摘水果，一天能采摘_______公斤.（2分）（2）张家和王家均雇人采摘水果，王家雇的人数是张家的2倍，张家的人手工采摘，王家所雇的人中的32用采摘机采摘，31用手工采摘.已知手工采摘1公斤水果的费用是1.5元，设张家雇佣x 人.①用含x 的代数式表示：王家雇佣的人数：_________人；王家雇佣的人中用采摘机采摘人数：__________人.（2分） ②张家付给雇工一天的工资总额为1440元，求x 的值是多少？（4分）28. （10分）若数轴上点A 表示有理数a ，点B 表示有理数b ，则AB 的中点表示的数可用公式2ba +求得，如点B A 、表示的数分别是2-和4，则线段AB 的中点所表示的数是1242-=+. （1）如图1，点A 所表示的数是2-，点B 所表示的数是4，则AB 的距离是_______;（1分）（2）若点M 表示的数是3-，线段MN 的中点所表示的数是2，则点N 表示的数是__________;（2分）（3）如图1，点A 、点D 、点B 表示的数分别是432-，，，两个动点Q P 、分别从点A 和点B 同时出发，点P 以每秒3个单位长度的速度向右运动，点Q 以每秒1个单位长度的速度向右运动。