高考押题卷(五)

2023年全国高考冲刺押题卷五语文2023年全国高考冲刺押题卷五语文参考内容：一、作文题目：《科技之光，人文之温——数字时代下的人与科技关系》参考内容：1. 科技的迅猛发展在数字时代对人们生活产生了巨大影响，深刻改变了人与科技之间的关系。

2. 科技的快速发展提供了更多的便利和高效率，无论是通信、交通、医疗还是教育等领域，科技为人们的生活和工作带来了莫大的便利。

3. 然而，科技的迅速发展也带来了一系列的隐忧。

数字时代的科技普及和信息爆炸带来的信息泛滥让人们面临无法快速有效获取有效信息的问题。

4. 在数字时代，以科技为核心的产业快速发展，给社会带来了更多的非人性化问题。

例如，在人工智能领域，人与机器的界限逐渐模糊，人们面临着是否能保持人类独有的思考能力和情感交流能力的困扰。

5. 数字时代的科技高速发展也对人们的思维方式和价值观产生了深远的影响。

信息爆炸和碎片化的阅读习惯使人们趋于浅阅读和碎片化思维，长时间使用智能手机等电子设备对人们的专注力和理解力产生负面影响。

6. 面对科技的迅猛发展，人们需要保持思辨精神和人文关怀，用科技服务于人的情怀和热爱，充分发挥科技在促进社会进步和人类发展中的重要作用。

7. 教育是科技与人之间关系的重要纽带。

通过科技创新教育模式，个性化教学和在线教育等手段，使科技与教育深度融合，提高学生学习效果和学科素养。

8. 在数字时代，要坚持传统技艺的传承和人文关怀的提升，推动科技与人文相互融合。

科技的发展需要人文精神的引导，有人文关怀的科技才能真正服务于人类的需求。

9. 人们要注重自我保护，加强对信息的筛选和分辨能力，培养深度阅读的习惯，提高自己的思辨能力和概括能力。

10. 人们应当正确看待科技发展的利弊，用科技为人服务，用科技提高人类文明的发展水平。

以上是2023年全国高考冲刺押题卷五语文参考内容，希望能对考生们的备考有所帮助。

152023年高考化学仿真押题模拟试卷及答案（五）可能用到的相对原子质量：H 1 C 12 N 14 O 16 Na 23 Mg 24 Al 27 S 32 Cl 35.5K 39 Ca 40 Mn 55 Fe 56 Cu 64 Zn 65 Ag 108选择题单项选择题：本题包括 10 小题, 每小题 2 分, 共计 20 分。

每小题只．有．一．个．选．项．符合 题意。

1．2017 年世界地球日我国的主题为“节约集约利用资源,倡导绿色简约生活”。

下列做法应提倡的是A ．夏天设定空调温度尽可能的低B ．推广使用一次性塑料袋和纸巾C ．少开私家车多乘公共交通工具D ．对商品进行豪华包装促进销售2．下列有关化学用语表示正确的是A ．质量数为 31 的磷原子：31PB ．氟原子的结构示意图：C ．CaCl 2 的电子式：D ．明矾的化学式：Al 2(SO 4)3 3．下列有关物质性质与用途具有对应关系的是A ．Na 2O 2 吸收 CO 2 产生 O 2，可用作呼吸面具供氧剂B ．ClO 2 具有还原性，可用于自来水的杀菌消毒C ．SiO 2 硬度大，可用于制造光导纤维D ．NH 3 易溶于水，可用作制冷剂4．下列制取 SO 2、验证其漂白性、收集并进行尾气处理的装置和原理能达到实验目的的是5．短周期主族元素 X 、Y 、Z 、W 原子序数依次增大，其中只有 Y 、Z 处于同一周期且相邻，Z 是地壳中含量最多的元素，W 是短周期中金属性最强的元素。

下列说法正确的是A．原子半径：r(X)＜r(Y)＜r(Z)＜r(W)B．W 的最高价氧化物的水化物是一种弱碱C．Y 的单质的氧化性比Z的强2 通电 2 212 2 222 23 233 3 3242 3 32D ．X 、Y 、Z 三种元素可以组成共价化合物和离子化合物 6．下列指定反应的离子方程式正确的是A ．钠与水反应：Na ＋2H 2O ＝Na ＋＋2OH －＋H ↑B ．电解饱和食盐水获取烧碱和氯气：2Cl －＋2H O ===== H ↑＋Cl ↑＋2OH－222C ．向氢氧化钡溶液中加入稀硫酸：Ba 2＋＋OH －＋H ＋＋SO 2－＝BaSO ↓＋H O44 2D ．向碳酸氢铵溶液中加入足量石灰水：Ca 2＋＋HCO －＋OH －＝CaCO ↓＋H O3327．在给定条件下，下列选项所示的物质间转化均能实现的是Cl 2NaOH(aq)O 2H 2OA ．Fe ---------→ FeCl 2 ---------→ Fe(OH)2B ．S ---------→ SO 3 -------→ H 2SO 4点燃点燃高温 SiO 2O 2 H 2OC ．CaCO 3 -------→ CaO ---------→ CaSiO 3D ．NH 3 ------------→ NO -------→ HNO 3高温催化剂，△8．通过以下反应可获得新型能源二甲醚(CH 3OCH 3 )。

2022年高考临考押题卷（五）数学（新高考卷）（考试时间：120分钟 试卷满分：150分）注意事项：1．本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分。

答卷前，考生务必将自己的姓名、准考证号填写在答题卡上。

2．回答第Ⅰ卷时，选出每小题答案后，用2B 铅笔把答题卡上对应题目的答案标号涂黑。

如需改动，用橡皮擦干净后，再选涂其他答案标号。

写在本试卷上无效。

3．回答第Ⅱ卷时，将答案写在答题卡上。

写在本试卷上无效。

4．考试结束后，将本试卷和答题卡一并交回。

一、 单项选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求.1．已知集合{}240A x x =->，{}0,1,2,3B =，则()R A B ⋂=（ ）A ．{0}B ．{0，1}C ．{1，2}D ．{0，1，2}【答案】D 【解析】 【详解】因为(){}[]2R 402,2A x x =-≤=-，{}0,1,2,3B =，所以()R A B ⋂={}0,1,2， 故选：D 2．已知13i1iz -=+（i 是虚数单位）的共轭复数为z ，则z 在复平面上对应的点位于（ ） A ．第一象限 B ．第二象限C ．第三象限D ．第四象限【答案】B 【详解】 因为()()()()13i 1i 13i 24i12i 1i 1i 1i 2z -----====--++-，则12i z =-+， 因此，z 在复平面上对应的点位于第二象限. 故选：B.3．“4a <”是“过点()1,1有两条直线与圆2220x y y a ++-=相切”的（ ）A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件【答案】B 【详解】由已知得点()1,1在圆2220x y y a ++-=外，所以22211210240a a ⎧++⨯->⎨+>⎩，解得14a -<<， 所以“4a <”是“过点()1,1有两条直线与圆2220x y y a ++-=相切”的必要不充分条件， 故选：B4．若圆锥的母线长为36π，则该圆锥的体积是（ ） A 3π B ．3π C ．33π D ．9π【答案】B 【详解】设圆锥的高为h ，底面半径为r ， 则122362r ππ⨯⨯，解得3r =所以()()222333h =-.则圆锥的体积13333V ππ=⨯⨯=.故选：B5．已知函数()()sin 30f x x x πωπωω=>在()0,1内恰有3个极值点和4个零点，则实数ω的取值范围是（ ） A ．1023,36⎛⎤ ⎥⎝⎦B ．1013,33⎡⎫⎪⎢⎣⎭C ．1713,63⎛⎤ ⎥⎝⎦D ．1723,66⎛⎤ ⎥⎝⎦【答案】A 【详解】()sin 32sin 3ππωπωπω⎛⎫==- ⎪⎝⎭f x x x x ，因为()0,1x ∈，所以,333ππππωωπ⎛⎫-∈-- ⎪⎝⎭x ， 又因为函数()()sin 30f x x x πωπωω=>在()0,1内恰有3个极值点和4个零点，由图像得：7332πππωπ<-≤解得：102336ω<≤，所以实数ω的取值范围是1023,36⎛⎤ ⎥⎝⎦.故选：A.6．若直线l ：2150x y -=经过双曲线M ：22221x y a b -=的一个焦点，且与双曲线M 有且仅有一个公共点，则双曲线M 的方程为（ ） A ．221520x y -=B ．221205x y -=C ．221312x y -=D ．221123y x -= 【答案】D 【详解】令0y =得15x =l 与x 轴的交点为)15,0，所以双曲线M 的右焦点为)15,0，则15c =即22215c a b =+=①，直线l 与双曲线M 有且仅有一个公共点，直线l 又过双曲线的焦点， 所以直线l 与双曲线的一条渐近线by x a=平行， 即12b a =②， 由①②得解得2212,3a b ==，所以双曲线的方程为221123y x -= 故选：D.7．某市抽调5位医生分赴4所医院支援抗疫，要求每位医生只能去一所医院，每所医院至少安排一位医生.由于工作需要，甲､乙两位医生必须安排在不同的医院，则不同的安排种数是（ ） A ．90 B ．216 C ．144 D ．240【答案】B 【详解】完成这件事情，可以分两步完成，第一步，先将5为医生分为四组且甲、乙两位医生不在同一组，共有2519C -=种方案；第二步，再将这四组医生分配到四所医院，共有4424A =种不同方案，所以根据分步乘法计数原理得共有249216⨯=种不同安排方案.故选：B.8．设()f x 是定义域为R 的偶函数，且在[)0,∞+上单调递增，若2log3a f ⎛= ⎝，3log 2b f ⎛= ⎝，433c f -⎛⎫=- ⎪⎝⎭，则a ，b ，c 的大小关系为（ ）A ．c b a >>B ．b c a >>C ．a c b >>D ．a b c >>【答案】D 【详解】依题意()f x 是定义域为R 的偶函数，()()12122222loglog 3log 3log 33a f f f f -⎛⎫⎛===-= ⎪ ⎝⎝⎭， ()()12123333loglog 2log 2log 22b f f f f -⎛⎫⎛===-= ⎪ ⎝⎝⎭， 443333c f f --⎛⎫⎛⎫=-= ⎪ ⎪⎝⎭⎝⎭，22log 3log 21>=，331113333328,33,23,23⎛⎫⎛⎫==>> ⎪ ⎪⎝⎭⎝⎭，1333311log 3log 2log 33=>>=，41310333--<<=， 由于()f x 在[)0,∞+上单调递增，所以a b c >>. 故选：D二、多项选择题：本题共4小题，每小题5分，共20分.在每小题给出的选项中，有多项符合题目要求.全部选对的得5分，部分选对的得3分，有选错的得0分.9．下列说法正确的是（ ）A ．将一组数据中的每一个数据都加上同一个常数后，方差不变B ．设具有线性相关关系的两个变量x ，y 的相关系数为r ，则r 越接近于0，x 和y 之间的线性相关程度越强C ．在一个22⨯列联表中，由计算得2K 的值，则2K 的值越小，判断两个变量有关的把握越大D ．若()2~1,X N σ，()20.2P X >=，则()010.3P X <<=【答案】AD 【详解】对于A ，设12,,,n x x x ⋅⋅⋅的平均数为x ，方差为2s ，则 21()n x x x x n=++⋅⋅+，2222121[()()()]n s x x x x x x n =-+-+⋅⋅⋅+-，给12,,,n x x x ⋅⋅⋅中每一个数同时加上a ，则得到一组新的数为12,,,n x a x a x a ++⋅⋅⋅+，则其平均数为x x a '=+，所以新的数据的方差为22222121[()()()]n s x a x a x a x a x a x a s n'=+--++--+⋅⋅⋅++--=，即方差不变，所以A 正确，对于B ，由相关系数的性质可知，设具有线性相关关系的两个变量x ，y 的相关系数为r ，则r 越接近于0，x 和y 之间的线性相关程度越弱，所以B 错误，对于C ，在一个22⨯列联表中，由计算得2K 的值，则2K 的值越大，判断两个变量有关的把握越大，所以C 错误，对于D ，因为()2~1,X N σ，()20.2P X >=，所以()00.2P X <=，所以()101(120.2)0.32P X <<=⨯-⨯=，所以D 正确，故选：AD 10．已知向量()2,1a =，()()cos ,sin 0b θθθπ=≤≤，则下列命题正确的是（ ）A ．若a b ⊥，则tan 2θ=B ．若b 在a 上的投影为36a ，则向量a 与b 夹角为23π C ．与a 共线的单位向量只有一个为63⎝⎭D ．存在θ，使得a b a b +=+ 【答案】BD 【详解】 解：向量()2,1a =，()()cos ,sin 0b θθθπ=≤≤，对A ：因为a b ⊥2sin 0θθ+=，所以tan 2θ=-A 错误；对B ：因为b 在a 上的投影向量为36a ，即3cos ,6b a b a <>=-， 所以3cos ,6a b a b<>=-，又()2221cos sin 1,213b a θθ=+==+=所以31cos ,3612a b <>=-=-⨯， 因为[],0,a b π<>∈，所以向量a 与b 夹角为23π，故选项B 正确； 对C ：与a 共线的单位向量有两个，分别为63⎝⎭和63⎛ ⎝⎭，故选项C 错误； 对D ：当63cos θθ==3a b =，此时向量a 与b 共线同向，满足a b a b +=+，所以存在θ，使得a b a b +=+，故选项D 正确； 故选：BD.11．若直线0x y m ++=上存在点P ，过点P 可作圆22:1O x y +=的两条切线P A ，PB ，切点为A ，B ，且90APB ∠=，则实数m 的取值可以为（ ）A ．3B ．2C ．0D ．1-【答案】BCD 【详解】若90APB ∠=，因为,⊥⊥PA AO PB BO ， 所以AOB 90∠=，又1AO BO ==，所以四边形AOBP 是边长为1的正方形，所以对角线2PO等价于直线0x y m ++=与圆222x y +=有公共点，22≤m ，解之可得[]2,2∈-m ，故选：BCD.12．已知同底面的两个正三棱锥P ABC -和Q ABC -均内接于球O ，且正三棱锥P ABC -的侧面与底面所成角的大小为π4，则下列说法正确的是（ ）.A ．//PA 平面QBCB ．设三棱锥Q ABC -和P ABC -的体积分别为Q ABC V -和P ABC V -，则4Q ABC P ABC V V --= C ．平面ABC 截球O 所得的截面面积是球O 表面积的425倍D ．二面角P AB Q --的正切值为53-【答案】BCD 【详解】∵同底面的两个正三棱锥P ABC -和Q ABC -均内接于球O ， ∴PQ 为球O 的直径，取AB 的中点M ，连接PM 、QM ，则PM ⊥AB ，CM ⊥AB ，QM ⊥AB ，∴∠PMC 为侧面PAB 与底面ABC 所成二面角的平面角，∠QMC 为侧面QAB 与底面ABC 所成二面角的平面角，又正三棱锥P ABC -的侧面与底面所成角的大小为π4，设底面的中心为N ，P 到底面的距离为h ，球的半径为R ，则PN=h ，OP=R ，ON=R －h ，MN=h ，CN=2h ， ∴()()2222R h R h =+-， ∴52R h =，QN=4h ，PN=h ，∴P 、C 、Q 、M 四点共面，又CN=2MN ，QN=4h ，PN=h ， ∴PA 与QM 不平行，故PA 与平面QBC 不平行，故A 错误； 由QN=4PN ，可得4Q ABC P ABC V V --=，故B 正确； ∵平面ABC 截球O 所得的截面面积为()2224h h ππ=，球O 表面积为222544252h R h πππ⎛⎫== ⎪⎝⎭，∴平面ABC 截球O 所得的截面面积是球O 表面积的425倍，故C 正确； ∵(),,2224175PM h QM h h h QP h ==+=，∴()()()cos 22221753221734h h h PMQ h h+-∠==-⋅⋅，sin 534PMQ ∠=，∴tan 53PMQ ∠=-，即二面角P AB Q --的正切值为53-，故D 正确.故选：BCD.三、填空题：本题共4小题，每小题5分，共20分13．抛物线28x y =焦点为F ，准线为l ，P 为抛物线上一点，PA l ⊥，A 为垂足，如果直线AF 的倾斜角等于60︒，那么PF 等于__________. 【答案】83【详解】解：在APF 中，由抛物线的定义，可得||||PA PF =，||sin604AF ︒=，8||3AF ∴=，又PA l ⊥，则PA y ∕∕轴， 又30AFO PAF PFA ∠=∠=∠=︒， 过P 作PB AF ⊥于B ，则1423BF AF ==， 则||8||cos303BF PF ==︒． 故答案为：8314．设()f x 是定义在R 上且周期为2的函数，在区间[)1,1-上(),102,015x a x f x x x +-≤<⎧⎪=⎨-≤<⎪⎩,其中R a ∈.若5922f f ⎛⎫⎛⎫-= ⎪ ⎪⎝⎭⎝⎭，则()2022f a 的值是____________. 【答案】25-##-0.4【详解】解：因为()f x 是定义在R 上且周期为2的函数，在区间[)1,1-上(),102,015x a x f x x x +-≤<⎧⎪=⎨-≤<⎪⎩, 所以511222f f a ⎛⎫⎛⎫-=-=-+ ⎪ ⎪⎝⎭⎝⎭，92221115210f f ⎛⎫⎛⎫==-=- ⎪ ⎪⎝⎭⎝⎭，又5922f f ⎛⎫⎛⎫-= ⎪ ⎪⎝⎭⎝⎭，即11210a -+=-，解得25a =， 所以()24424220222022808555555f a f f f⎛⎫⎛⎫⎛⎫=⨯=+==-=- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭， 故答案为：25-.15．在正项等比数列{}n a 中，若484a a =，则22210log log a a +=______． 【答案】2 【详解】()()2221022102482log log log log log 42a a a a a a +====．故答案为：216．已知奇函数()f x 在区间(),0∞-上是增函数，且()21f -=-，()10f =，当0x >，0y >时，都有()()()f xy f x f y =+，则不等式()3log 10f x +<的解集为______．【答案】()()1114,22,1,1,242⎛⎫⎛⎫--⋃--⋃⋃ ⎪ ⎪⎝⎭⎝⎭【详解】不等式3log |()1|0f x +<等价为0|()1|1f x <+<， 即0()11f x <+<或1()10f x -<+<， 即1()0f x -<<或2()1f x -<<-，()f x 是奇函数，且(2)1,(1)0f f -=-=，(2)1,(1)0f f ∴=-=，故11(1)(2)(2)()022f f f f =⨯=+= ，则1()12f =- ，11111()()()()242222f f f f =⨯=+=-， (4)(4)(2)(2)2f f f f -=-=--=- ，又奇函数()f x 在区间(,0)-∞上是增函数 ，故()f x 在区间(0,)+∞上也是增函数， 故1()0f x -<<即(2)()(1)f f x f -<<-或1()()(1)2f f x f <<， 此时1(2,1)(,1)2x ∈-- ；而2()1f x -<<-即(4)()(2)f f x f -<<- 或11()()()42f f x f <<，此时11(4,2)(,)42x ∈-- ；故不等式()3log 10f x +<的解集为()()1114,22,1,1,242⎛⎫⎛⎫--⋃--⋃⋃ ⎪ ⎪⎝⎭⎝⎭，故答案为：()()1114,22,1,1,242⎛⎫⎛⎫--⋃--⋃⋃ ⎪ ⎪⎝⎭⎝⎭四、解答题：本小题共6小题，共70分。

01一、现代文阅读(共35分）(本题17分)阅读下面的文字，完成下面小题。

材料一：①在讲述故事的同时发表议论，不论在传统的叙事文类中，还是在现代小说里，都是作者（故事讲述者）的天然权利。

议论和叙事，两者相辅相成，是小说和故事重要的结缔组织。

议论的作用也是多种多样的。

有时，议论代表了作者或叙事代言人的声音，寻求与读者（听众）进行直接的交流；有时，发表议论的，是小说或故事中的人物——不同人物对事件的看法，在文本中构成复杂的对话关系；当然，议论的运用，有时候仅仅是为了改变或调节叙事节奏；诸如此类。

不管怎么说，议论的使用，或许与小说或故事本身一样古老，同时，经过一系列改头换面的乔装打扮，一直延续至今。

②列夫·托尔斯泰如果想在写作中发表议论的话，往往会随时中断引人入胜的故事，并将它遥遥无期地搁置起来。

他似乎并不在乎读者对这种突兀的做法有什么看法。

在《战争与和平》中，这样的例子非常多。

巴尔扎克的做法也差不多。

似乎伟大作家的标志之一，就是拥有随时发表议论的特权。

就算你知道巴尔扎克在小说的某处要展开洋洋洒洒的议论了，就算你对作家的这种做法感到很不耐烦，在一般情况下，19世纪的读者还是会立刻被他博学、风趣、睿智的议论文字吸引住，不太舍得“跳读”。

③不过，不知从何时开始，议论，甚至包括与议论直接相关的“讲述”和“概要叙事”，都成了小说写作的禁忌。

作家们被告知，最好不要在作品中发表什么议论，而应该将议论所要呈现的内容通过人物的行为，自然而然地显示出来。

伴随着对列夫·托尔斯泰以及巴尔扎克几乎众口一词的批评，议论最小化成了现代小说的某种“金科玉律”。

比如说，在小说中做出“包法利夫人走向了壁炉”这样的暗示，要比直接交代“包法利夫人感觉有些冷”，显得更为“高级”。

久而久之，当代小说形成了某种不成文的箴规：“场景叙事”总要比“概要叙事”好；“显示”总要比“讲述”好；通过人物行动来显示意义，总要比直接付诸议论和交代好。

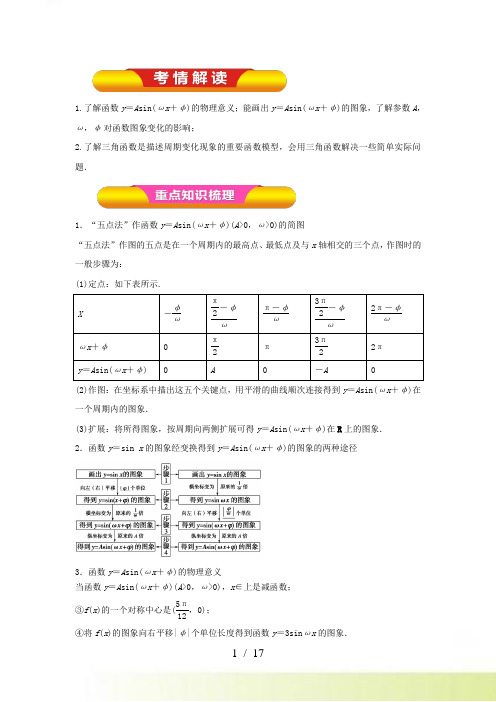
1.了解函数y ＝A sin(ωx ＋φ)的物理意义；能画出y ＝A sin(ωx ＋φ)的图象，了解参数A ，ω，φ对函数图象变化的影响；2.了解三角函数是描述周期变化现象的重要函数模型，会用三角函数解决一些简单实际问题．1．“五点法”作函数y ＝A sin(ωx ＋φ)(A >0，ω>0)的简图“五点法”作图的五点是在一个周期内的最高点、最低点及与x 轴相交的三个点，作图时的一般步骤为： (1)定点：如下表所示.X－φωπ2－φωπ－φω3π2－φω2π－φωωx ＋φ0 π2π 3π2 2π y ＝A sin(ωx ＋φ)A－A(2)作图：在坐标系中描出这五个关键点，用平滑的曲线顺次连接得到y ＝A sin(ωx ＋φ)在一个周期内的图象．(3)扩展：将所得图象，按周期向两侧扩展可得y ＝A sin(ωx ＋φ)在R 上的图象． 2．函数y ＝sin x 的图象经变换得到y ＝A sin(ωx ＋φ)的图象的两种途径3．函数y ＝A sin(ωx ＋φ)的物理意义当函数y ＝A sin(ωx ＋φ)(A >0，ω>0)，x ∈上是减函数； ③f (x )的一个对称中心是(5π12，0)；④将f (x )的图象向右平移|φ|个单位长度得到函数y ＝3sin ωx 的图象．答案 ①③③：令x ＝5π12⇒f (x )＝3sinπ＝0，正确．④：应平移π12个单位长度，错误．【高考新课标1文数】若将函数y =2sin (2x +π6)的图像向右平移14个周期后，所得图像对应的函数为（ ）（A ）y =2sin(2x +π4) （B ）y =2sin(2x +π3) （C ）y =2sin(2x –π4) （D ）y =2sin(2x –π3)【答案】D【解析】函数2sin(2)6y x π=+的周期为π，将函数2sin(2)6y x π=+的图像向右平移14个周期即4π个单位，所得图像对应的函数为2sin[2())]2sin(2)463y x x πππ=-+=-，故选D.【高考四川文科】为了得到函数sin()3y x π=+的图象，只需把函数y=sinx 的图象上所有的点( )(A)向左平行移动3π个单位长度 (B) 向右平行移动3π个单位长度 (C) 向上平行移动3π个单位长度 (D) 向下平行移动3π个单位长度【答案】A【解析】由题意，为得到函数sin()3y x π=+，只需把函数sin y x =的图像上所有点向左移3π个单位，故选A. 【高考上海文科】设aR ，[0,2π]b .若对任意实数x 都有πsin(3)=sin()3xax b ，则满足条件的有序实数对(a ，b )的对数为（ ）(A)1 (B)2 (C)3 (D)4 【答案】B【高考新课标Ⅲ文数】函数sin 3y x x =的图像可由函数2sin y x =的图像至少向右平移_____________个单位长度得到． 【答案】3π【解析】因为sin 32sin()3y x x x π==-，所以函数sin 3y x x =的的图像可由函数2sin y x =的图像至少向右平移3π个单位长度得到． 【高考新课标1文数】已知θ是第四象限角，且sin(θ+π4)=35，则tan(θ–π4)= .【高考山东，文4】要得到函数4y sin x =-（3π）的图象，只需要将函数4y sin x =的图象（ ） （A ）向左平移12π个单位 （B ）向右平移12π个单位（C ）向左平移3π个单位 （D ）向右平移3π个单位 【答案】B【解析】因为sin(4)sin 4()312y x x ππ=-=-，所以，只需要将函数4y sin x =的图象向右平移12π个单位，故选B.【高考湖北，文18】某同学用“五点法”画函数π()sin()(0,||)2f x A x ωϕωϕ=+><在某一个周期内的图象时，列表并填入了部分数据，如下表：x ωϕ+π2π3π22πxπ3 5π6sin()A x ωϕ+55-．．．．．．．．．．． 析式；（Ⅱ）将()y f x =图象上所有点向左平行移动π6个单位长度，得到()y g x =图象，求 ()y g x =的图象离原点O 最近的对称中心.【答案】（Ⅰ）根据表中已知数据，解得π5,2,6A ωϕ===-.数据补全如下表：x ωϕ+π2 π3π2 2πxπ12π37π125π613π12sin()A x ωϕ+ 050 5- 0且函数表达式为π()5sin(2)6f x x =-；（Ⅱ）离原点O 最近的对称中心为π(,0)12-.1．(·天津卷) 已知函数f (x )＝3sin ωx ＋cos ωx (ω＞0)，x ∈R.在曲线y ＝f (x )与直线y ＝1的交点中，若相邻交点距离的最小值为π3，则f (x )的最小正周期为( )A.π2B.2π3C ．π D．2π【答案】C【解析】∵f (x )＝2sin ⎝⎛⎭⎪⎫ωx ＋π6＝1， ∴sin ⎝⎛⎭⎪⎫ωx ＋π6＝12，∴ωx 1＋π6＝π6＋2k 1π(k 1∈Z)或 ωx 2＋π6＝5π6＋2k 2π(k 2∈Z)，则ω(x 2－x 1)＝2π3＋2(k 2－k 1)π.又∵相邻交点距离的最小值为π3，∴ω＝2，∴T ＝π. 2．(·安徽卷) 若将函数f (x )＝sin 2x ＋cos 2x 的图像向右平移φ个单位，所得图像关于y 轴对称，则φ的最小正值是( )A.π8B.π4 C.3π8 D.3π4 【答案】C3．(·重庆卷) 将函数f (x )＝sin(ωx ＋φ)⎝ ⎛⎭⎪⎫ω＞0，－π2≤φ＜π2图像上每一点的横坐标缩短为原来的一半，纵坐标不变，再向右平移π6个单位长度得到y ＝sin x 的图像，则f ⎝ ⎛⎭⎪⎫π6＝________． 【答案】22【解析】函数f (x )＝sin(ωx ＋φ)图像上每一点的横坐标缩短为原来的一半，得到y ＝sin(2ωx ＋φ)的图像，再向右平移π6个单位长度，得到y ＝sin2ωx －π6＋φ＝sin ⎝⎛⎭⎪⎫2ωx －ωπ3＋φ的图像．由题意知sin ⎝⎛⎭⎪⎫2ωx －ωπ3＋φ＝sinx ，所以2ω＝1，－ωπ3＋φ＝2k π(k ∈Z)，又－π2≤φ≤π2，所以ω＝12，φ＝π6，所以f (x )＝sin ⎝ ⎛⎭⎪⎫12x ＋π6，所以f ⎝ ⎛⎭⎪⎫π6＝sin ⎝ ⎛⎭⎪⎫12×π6＋π6＝sin π4＝22.4．(·北京卷) 函数f (x )＝3sin ⎝⎛⎭⎪⎫2x ＋π6的部分图像如图1­4所示．图1­4(1)写出f (x )的最小正周期及图中x 0，y 0的值； (2)求f (x )在区间⎣⎢⎡⎦⎥⎤－π2，－π12上的最大值和最小值．5．(·福建卷) 已知函数f (x )＝2cos x (sin x ＋cos x )． (1)求f ⎝ ⎛⎭⎪⎫5π4的值；(2)求函数f (x )的最小正周期及单调递增区间． 【解析】方法一： (1)f ⎝⎛⎭⎪⎫5π4＝2cos 5π4⎝ ⎛⎭⎪⎫sin 5π4＋cos 5π4＝－2cos π4⎝ ⎛⎭⎪⎫－sin π4－cos π4＝2.(2)因为f (x )＝2sin x cos x ＋2cos 2x ＝sin 2x ＋cos 2x ＋1 ＝2sin ⎝⎛⎭⎪⎫2x ＋π4＋1，所以T ＝2π2＝π，故函数f (x )的最小正周期为π.由2k π－π2≤2x ＋π4≤2k π＋π2，k ∈Z ，得k π－3π8≤x ≤k π＋π8，k ∈Z.所以f (x )的单调递增区间为⎣⎢⎡⎦⎥⎤k π－3π8，k π＋π8，k ∈Z.方法二：f (x )＝2sin x cos x ＋2cos 2x ＝sin 2x ＋cos 2x ＋16．(·广东卷) 若空间中四条两两不同的直线l 1，l 2，l 3，l 4满足l 1⊥l 2，l 2∥l 3，l 3⊥l 4，则下列结论一定正确的是( ) A ．l 1⊥l 4 B ．l 1∥l 4C ．l 1与l 4既不垂直也不平行D ．l 1与l 4的位置关系不确定 【答案】D【解析】本题考查空间中直线的位置关系，构造正方体进行判断即可．如图所示，在正方体ABCD ­A 1B 1C 1D 1中，设BB 1是直线l 1，BC 是直线l 2，AD 是直线l 3，则DD 1是直线l 4，此时l 1∥l 4；设BB 1是直线l 1，BC 是直线l 2，A 1D 1是直线l 3，则C 1D 1是直线l 4，此时l 1⊥l 4.故l 1与l 4的位置关系不确定．7．(·湖北卷) 某实验室一天的温度(单位：℃)随时间t (单位：h)的变化近似满足函数关系：f (t )＝10－3cos π12t －sin π12t ，t ∈ 函数f (x )＝sin(x ＋φ)－2sin φcos x 的最大值为________． 【答案】1【解析】 f (x )＝sin(x ＋φ)－2sin φcos x ＝sin x cos φ＋cos x sin φ－2sin φcos x ＝sin x cos φ－cos x sin φ＝sin(x －φ)，其最大值为1. 10．(·全国新课标卷Ⅰ] 在函数①y ＝cos|2x |，②y ＝|cos x |，③y ＝cos ⎝ ⎛⎭⎪⎫2x ＋π6，④y ＝tan ⎝ ⎛⎭⎪⎫2x －π4中，最小正周期为π的所有函数为( ) A ．①②③ B ．①③④ C ．②④ D ．①③ 【答案】A11．(·山东卷) 函数y ＝32sin 2x ＋cos 2x 的最小正周期为________． 【答案】π 【解析】因为y ＝32sin 2x ＋1＋cos 2x 2＝sin ⎝ ⎛⎭⎪⎫2x ＋π6＋12，所以该函数的最小正周期T ＝2π2＝π . 12．(·陕西卷) 函数f (x )＝cos ⎝ ⎛⎭⎪⎫2x ＋π4的最小正周期是( )A.π2 B ．π C．2π D．4π 【答案】B 【解析】T ＝2π2＝π.134．(·浙江卷) 为了得到函数y ＝sin 3x ＋cos 3x 的图像，可以将函数y ＝2cos 3x 的图像( )A ．向右平移π12个单位B ．向右平移π4个单位C ．向左平移π12个单位D ．向左平移π4个单位【答案】A【解析】y ＝sin 3x ＋cos 3x ＝2cos ⎝ ⎛⎭⎪⎫3x －π4＝2cos ⎣⎢⎡⎦⎥⎤3⎝ ⎛⎭⎪⎫x －π12，故将函数y ＝2cos 3x 的图像向右平移π12个单位可以得到函数y ＝sin 3x ＋cos 3x 的图像，故选A.14．(·四川卷) 为了得到函数y ＝sin(x ＋1)的图像，只需把函数y ＝sin x 的图像上所有的点( )A ．向左平行移动1个单位长度B ．向右平行移动1个单位长度C ．向左平行移动π个单位长度D ．向右平行移动π个单位长度 【答案】A【解析】由函数y ＝sin x 的图像变换得到函数y ＝sin(x ＋1)的图像，应该将函数y ＝sin x 图像上所有的点向左平行移动1个单位长度，故选A. 15. (·四川卷) 已知函数f (x )＝sin ⎝ ⎛⎭⎪⎫3x ＋π4.(1)求f (x )的单调递增区间；(2)若α是第二象限角，f ⎝ ⎛⎭⎪⎫α3＝45cos ⎝⎛⎭⎪⎫α＋π4cos 2α，求cos α－sin α的值．1．函数y ＝cos ⎝⎛⎭⎪⎫2x －π3的部分图象可能是( )答案 D解析 ∵y ＝cos ⎝⎛⎭⎪⎫2x －π3，∴当2x －π3＝0， 即x ＝π6时，函数取得最大值1，结合图象看，可使函数在x ＝π6时取得最大值的只有D.2．将函数y ＝sin(2x ＋φ)的图象沿x 轴向左平移π8个单位后，得到一个偶函数的图象，则φ的一个可能取值为( )A.3π4B.π4 C ．0 D ．－π4答案 B3.已知函数f (x )＝2sin(ωx ＋φ)(ω>0，且|φ|<π2)的部分图象如图所示，则函数f (x )的一个单调递增区间是( ) A ． B ． C ． D ． 答案 D解析 由函数的图象可得14T ＝23π－512π，∴T ＝π，则ω＝2.又图象过点(512π，2)，∴2sin(2×512π＋φ)＝2，∴φ＝－π3＋2k π，k ∈Z ，∵|φ|<π2，∴取k ＝0，则φ＝－π3，即得f (x )＝2sin(2x －π3)，其单调递增区间为，k ∈Z ，取k ＝0，即得选项D.4．已知曲线f (x )＝sin ωx ＋3cos ωx (ω＞0)相邻的两条对称轴之间的距离为π2，且曲线关于点(x 0,0)中心对称，若x 0∈⎣⎢⎡⎦⎥⎤0，π2，则x 0等于( )A.π12 B.π6 C.π3 D.5π12答案 C5．函数f (x )＝sin(2x ＋φ)⎝⎛⎭⎪⎫|φ|＜π2的图象向左平移π6个单位后所得函数图象的解析式是奇函数，则函数f (x )在⎣⎢⎡⎦⎥⎤0，π2上的最小值为( )A ．－32B ．－12C.12 D.32答案 A6.电流强度I (安)随时间t (秒)变化的函数I ＝A sin(ωt ＋φ)(A >0，ω>0,0<φ<π2)的图象如右图所示，则当t ＝1100秒时，电流强度是________安．答案 －5解析 由图象知A ＝10，T 2＝4300－1300＝1100，∴ω＝2πT＝100π.∴I ＝10sin(100πt ＋φ)．∵图象过点⎝⎛⎭⎪⎫1300，10，∴10sin(100π×1300＋φ)＝10，∴sin(π3＋φ)＝1，π3＋φ＝2k π＋π2，k ∈Z ，∴φ＝2k π＋π6，k ∈Z ，又∵0<φ<π2，∴φ＝π6.∴I ＝10sin ⎝ ⎛⎭⎪⎫100πt ＋π6，当t ＝1100秒时，I ＝－5安． 7．若函数f (x )＝sin(ωx ＋φ) (ω>0且|φ|<π2)在区间⎣⎢⎡⎦⎥⎤π6，2π3上是单调递减函数，且函数从1减小到－1，则f ⎝ ⎛⎭⎪⎫π4＝________.答案328．已知函数f (x )＝A sin(ωx ＋φ)(A ＞0，ω＞0，|φ|＜π2)在一个周期内的图象如图所示．若方程f (x )＝m 在区间上有两个不同的实数x 1，x 2，则x 1＋x 2的值为________．答案π3或43π 解析 由图象可知y ＝m 和y ＝f (x )图象的两个交点关于直线x ＝π6或x ＝23π对称，∴x 1＋x 2＝π3或43π.9．设函数f (x )＝32－3sin 2ωx －sin ωx cos ωx (ω>0)，且y ＝f (x )图象的一个对称中心到最近的对称轴的距离为π4.(1)求ω的值；(2)求f (x )在区间⎣⎢⎡⎦⎥⎤π，3π2上的最大值和最小值． 解 (1)f (x )＝32－3sin 2ωx －sin ωx cos ωx ＝32－3×1－cos2ωx 2－12sin2ωx ＝32cos2ωx －12sin2ωx ＝－sin ⎝⎛⎭⎪⎫2ωx －π3.依题意知2π2ω＝4×π4，ω>0，所以ω＝1.(2)由(1)知f (x )＝－sin ⎝ ⎛⎭⎪⎫2x －π3.当π≤x ≤3π2时，5π3≤2x －π3≤8π3.所以－32≤sin ⎝⎛⎭⎪⎫2x －π3≤1.所以－1≤f (x )≤32. 故f (x )在区间⎣⎢⎡⎦⎥⎤π，3π2上的最大值和最小值分别为32，－1. 10．已知函数f (x )＝3sin ωx cos ωx ＋cos 2ωx －12(ω>0)，其最小正周期为π2.(1)求f (x )的表达式；(2)将函数f (x )的图象向右平移π8个单位长度，再将图象上各点的横坐标伸长到原来的2倍(纵坐标不变)，得到函数y ＝g (x )的图象，若关于x 的方程g (x )＋k ＝0在区间上有且只有一个实数解，求实数k 的取值范围．解得－32<k≤32或k＝－1，所以实数k的取值范围是(－32，32]∪{－1}．。

宁夏石嘴山市2024高三冲刺（高考数学）统编版测试(押题卷)完整试卷一、单选题：本题共8小题，每小题5分，共40分 (共8题)第(1)题我国数学家陈景润在哥德巴赫猜想的研究中取得了世界领先的成果．哥德巴赫猜想是“每个大于2的偶数可以表示为两个素数的和”，如．在不超过30的素数中，随机选取两个不同的数，其和等于30的概率是A．B．C．D．第(2)题已知点是双曲线的左焦点，点是双曲线上在第一象限内的一点，点是双曲线渐近线上的动点，则的最小值为（）A．8B．5C．3D．2第(3)题若角为第二象限角，，则（）A．B．C．D．第(4)题函数的图象经过变换后得到函数的图象，则（）A．B．C．D．第(5)题设集合，，则（）A．B．C．D．第(6)题在正方体中，E，F分别是，的中点，则（）A．B．平面BCEC．D．平面第(7)题在平行四边形中，对角线与交于点，，则（）．A．B．C．D．第(8)题设集合，，则下列结论正确的是（）A．B．C．D．二、多选题：本题共3小题，每小题6分，共18分 (共3题)第(1)题已知三棱锥的所有棱长均相等，其外接球的球心为O．点E满足，过点E作平行于和的平面，分别与棱相交于点，则（）A．当时，平面经过球心OB．四边形的周长随的变化而变化C．当时，四棱锥的体积取得最大值D ．设四棱锥的体积为，则第(2)题已知曲线的方程为（且)，，分别为与轴的左、右交点，为上任意一点(不与，重合)，则（）A．若，则为双曲线，且渐近线方程为B．若点坐标为，则为焦点在轴上的椭圆C．若点的坐标为，线段与轴垂直，则D．若直线，的斜率分别为，，则第(3)题若定义在上的函数满足，且当时，，则下列结论正确的是（）．A．若，，，则B．若，则C．若，则的图像关于点对称D ．若，则三、填空题：本题共3小题，每小题5分，共15分 (共3题)第(1)题如图，矩形中，，，以为直径的半圆上有一点，若，则的最大值为___________.第(2)题在的内角，，的对边分别为，，，已知，则的值为_______.第(3)题已知为等边三角形，点G是的重心．过点G的直线l与线段AB交于点D，与线段AC交于点E．设，，则__________；与周长之比的取值范围为__________．四、解答题：本题共5小题，每小题15分，最后一题17分，共77分 (共5题)第(1)题在四棱锥中，，，，，、分别为直线，上的动点.(1)若异面直线与所成的角为，判断与是否具有垂直关系并说明理由；(2)若，，求直线与平面所成角的最大值.第(2)题已知数列的前项和为，且满足．(1)求数列的通项公式；(2)已知，求数列的前项和．第(3)题在中，角，，所对的边分别为，，，且.（1）求；（2）若，，求的周长.第(4)题如图所示，棱锥中，平面，，，，，，为中点，．(1)证明：B，C，M，N四点共面；(2)求直线AC与平面所成线面角的正弦值．第(5)题函数.（1）求在处的切线方程（为自然对数的底数）；（2）设，若，满足，求证：.。

安徽省合肥市2024高三冲刺（高考物理）部编版质量检测(押题卷)完整试卷一、单项选择题（本题包含8小题，每小题4分，共32分。

在每小题给出的四个选项中，只有一项是符合题目要求的）(共8题)第(1)题如图所示，在水平地面上有一质量为M、倾角为的斜面，斜面上表面光滑。

质量为m的小滑块自斜面顶端滑下，斜面始终保持静止，若可变，当取某数值时，地面所受摩擦力最大，此时地面对斜面支持力大小为（ ）A．B．C．D．第(2)题噪声会对人的心理、生理、生活与工作带来严重影响，通常用声强级(单位为dB)来表示噪声的大小．式中I为声强，单位是W/m2；I0＝10-12W/m2是人刚好能听到的声音强度．我国规定工作环境的噪声一般应低于85dB，则以下最接近该标准的声强是（）A．B．C．D．第(3)题2023年8月25日，我国新一代人造太阳“中国环流三号”首次实现100万安培等离子体电流下的高约束模式运行，创造了新的运行纪录。

此装置（如图所示）中发生的核反应方程为，下列判断正确的是（）A.此核反应为衰变B. X带负电C. γ来自D.该反应过程吸收能量第(4)题某兴趣小组想利用小孔成像实验估测太阳的密度。

设计如图所示的装置，不透明的圆桶一端密封，中央有一小孔，另一端为半透明纸。

将圆桶轴线正对太阳方向，可观察到太阳的像的直径为d。

已知圆桶长为L，地球绕太阳公转周期为T。

则估测太阳密度的表达式为（ ）A．B．C．D．第(5)题如图1所示，横截面为直角的斜槽与水平方向的夹角为，横截面为正方形的长方体型物体恰好沿斜槽匀速下滑，斜槽横截面MON如图2所示，过斜槽底部OP的竖直面（图中未画出）与斜槽横截面M0N相交处为虚线OO′，MO与虚线OO′的夹角也为，斜槽两侧面为同种材料。

物体与斜槽的动摩擦因数等于（ ）A．tan B．C．D．cot第(6)题如图，一列简谐横波沿轴正方向传播，实线和虚线分别表示t 1=0和t2=0.5s（T>0.5s）时的波形，能正确反映时波形的是图（ ）A．B．C．D．第(7)题如图所示，一玻璃柱体的横截面是圆心角为90°的扇形MON。

2020年普通高等学校招生全国统一考试（全国三卷）语文押题卷（五）（解析版）注意事项：1．答卷前，考生务必将自己的姓名、准考证号填写在答题卡上。

2．作答时，务必将答案写在答题卡上，写在本试卷及草搞纸上无效。

3．考试结束后，将本试卷和答题卡一并交回。

一、现代文阅读（36分）（一）论述类文本阅读（本题共3小题，9分）阅读下面的文字，完成1～3题。

一、阅读下面的文字，完成下列（1—3）题。

①唐诗之所以能达到高峰，也有文人们的自觉努力，其中有些因素仍然值得当代文艺工作者思考。

②唐代经历了由盛而衰的变化过程，在治乱两种不同的时世中，文学都取得了极高成就。

其中至关重要的原因，是文人们在不同时代条件下都能将个人和国家命运联系在一起，具有为时代而创作的强烈责任感。

例如初盛唐是社会走向兴盛的时期，文人们能站在观察宇宙历史变化规律的高度，对时代和人生进行自觉的思考，将欣逢盛世的自豪感和自信心转化为积极进取的精神和健康乐观的情怀，创作出能充分体现时代风貌的优秀作品，从而形成文学繁荣与社会繁荣相一致的盛况。

③齐梁陈隋时期诗风愈趋浮靡，唐朝为吸取前朝覆亡的教训，从开国之初就将政治革新和文风革新联系在一起。

从初唐到盛唐，诗歌经历过三次重要革新。

其主要方向是提倡诗歌文质兼备，核心内涵是发扬比兴寄托的风雅传统，肃清浮华绮丽的文风。

初唐四杰针对唐高宗龙朔年间“以绮错婉媚为本”的“上官体”诗风，明确提出要廓清诗赋的“积年绮碎”，强调刚健的气骨和宏博的气象。

陈子昂标举风雅兴寄和建安气骨，肯定革新诗歌的关键在于恢复建安文人追求人生远大理想的慷慨意气，批判齐梁诗的“彩丽竞繁，而兴寄都绝”，提倡“骨气端翔、音情顿挫”的诗风。

张说和张九龄更进一步提出作文要风骨和文采并重，典雅和滋味兼顾，鼓励多样化的内容和风格，并提出盛唐诗歌应当以“天然壮丽”为主的审美理想。

经过这三次革新，建安气骨在开元中为诗人们广泛接受。

政治气象的更新又促使诗人们把共同的时代感受反映到诗里，并意识到他们渴望及时建功立业的人生理想正是建安气骨和时代精神的契合点。

决胜2024年高考数学押题预测卷05数 学（新高考九省联考题型）（考试时间：120分钟 试卷满分：150分）注意事项：1．本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分。

答卷前，考生务必将自己的姓名、准考证号填写在答题卡上。

2．回答第Ⅰ卷时，选出每小题答案后，用2B 铅笔把答题卡上对应题目的答案标号涂黑。

如需改动，用橡皮擦干净后，再选涂其他答案标号。

写在本试卷上无效。

3．回答第Ⅱ卷时，将答案写在答题卡上。

写在本试卷上无效。

4．考试结束后，将本试卷和答题卡一并交回。

一、选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．某地有8个快递收件点，在某天接收到的快递个数分别为360，284，290，300，188，240，260，288，则这组数据的百分位数为75的快递个数为（ ）A. 290 B. 295 C. 300 D. 330【答案】B【解析】将数据从小到大排序为：188，240，260，284，288， 290，300，360，875%6´=，所以75%分位数为2903002952+=.故选：B2．已知复数z 满足1i 1z z -=+，则z =（ ）A. i B.14C. 12D. 1【答案】D【解析】()11ii 1i i 1i 1i 11iz z z z z z -+=Þ-=+Þ-=+Þ=+-，故()()()2221i 1i 12i+i 2ii 1i 1i 1i 1i 2z +++=====--+-，故i z =-，故1z =.故选：D 3． 若20201918219200121920(2)a b x a x a b x a b x ab x b -=+++++L ，则19x =（ ）A. 20-B. 19202-´ C. 192- D. 19202´【答案】B【解析】因为20(2)a b -的展开通项公式为()()()20202020C 22C 020,N rrr r rr r r T a b a b r r --=-=-££Î，则1919191920(2)C 202x =-=-´，故B 正确．故选：B ．4．已知()1,1a =r ，(),1b m =-r ，m 为实数，若()a ab ^-r r r ，则向量a r 在b r上的投影向量为（ ）A. 13,55æöç÷èøB. 13,55æö-ç÷èøC. 31,55æöç÷èøD. 31,55æö-ç÷èø【答案】D【解析】根据题意可知()1,2a b m -=-rr ，由()a a b ^-r r r 可得()()11120a a b m ×-=´-+´=rr r ，解得3m =，所以()3,1b =-r ；所以向量a r 在b r15531,5b æö-ç÷è=ø=r r .故选：D5．已知圆22:4O x y +=，弦过定点()1,1P，则弦长AB 不可能的取值是（ ）A. B. C. 4D. 【答案】D【解析】圆22:4O x y +=的半径2r =，因为221124+=<，所以点()1,1P 在圆O 内，当弦AB 过圆心时，max24AB r ==，最短，=，所以弦长AB 不可能的取值是D 选项.故选：D.6．若24x y -=x ，R y Î，则x y -的最小值为（）A. 12B. 32C.54 D. 4【答案】C【解析】因为2x 所以2224444xx yyyy-===++．因为20y >，所以244y y +³所以5444x y -³=，即54x y -³．当且仅当244yy =，24x y =+14y =，32x =时等号成立，所以x y -的最小值为54．故选：C ．7．在ABC V 中，角,,A B C 所对的边分别为,,a b c ，2sin sin 3sin a A b B c C -=，若S 表示ABC V 的面积，则2Sb 的最大值为（ ）【答案】D【解析】因为2sin sin 3sin a A b B c C -=，由正弦定理得22223a b c -=，所以2221322a b c =+，由余弦定理得22222cos 24b c a b c A bc bc+--==，所以222224222422421(sin )sin (1cos )1182((1)4464bc A S c A c A c c b b b b b b -====-+-，令22c t b=，则22215((181)644S t t b =-+-£，当且仅当9t =，即3c b =时取等号，所以2S b £故选：D.8．已知22()32ln ,{1,1},(),{1,2,3,4}f x a ax x a g x bx x b =+Î-=-Î，使()()f x g x >恒成立的有序数对(,)a b 有（ ）A. 2个 B. 4个 C. 6个 D. 8个【答案】B【解析】由题得函数定义域为(0,)+¥，要想()()f x g x >恒成立，即2232ln a ax x bx x +>-恒成立，只需232ln a a x b x x +>-恒成立，只需232ln a x a x b x++>恒成立，设223(3)()()2ln (0),()a x a x a h x x a x x h x x x+-¢=++>=，所以当1a =-时，则min ()(3)42ln 3h x h ==-，使()()f x g x >恒成立的b 可取1；所以当1a =，则min ()(1)4h x h ==，使()()f x g x >恒成立的b 可取1，2，3，所以(,)a b 一共有(1,1),(1,1),(12),,(1,3)-共4种.故选：B ．二、选择题：本题共3小题，每小题6分，共18分.在每小题给出的选项中，有多项符合题目要求.全部选对的得6分，部分选对的得部分分，有选错的得0分.9．若11z z -=+，则（ ）A. R z Î B. 11z z -=+C. 0z z += D. 2z z z ×=【答案】BC【解析】利用复数的几何意义知在复平面内，z 对应的点在()()1,0,1,0-对应线段的中垂线即y 轴上，所以z 不一定是实数，所以A 错误；因为z 与z 关于实轴对称，且在y 轴上，所以B ，C 正确；取i z =，则21,1z z z ×==-，所以D 错误．故选：BC.10．如图，在正四棱台1111ABCD A B C D -中，111224,AB A B AA P ===为棱1CC 上一点，则（ ）A. 不存在点P ，使得直线BP P 平面11AB DB. 当点P 与1C 重合时，直线1CC ^平面BPDC. 当P 为1CC 中点时，直线BP 与ADD. 当P 为1CC 中点时，三棱锥111A A B D -与三棱锥P BCD -的体积之比为1:2【答案】BCD【解析】连接AC 交BD 于O ，因为正四棱台1111ABCD A B C D -，所以以OA 为x 轴，OB 为y 轴，垂直于平面ABCD 为z 轴建立如图所示坐标系，设点1A 在底面投影为E ，则AE OA OE =-=1A E ==11ABCD A B -则(A ，()0,B ，)C ，(1B ，(1C ，(10,D ，所以(1AB =-，(1AD =-uuuu r ，1CC =uuuu r ，()BC =--uuu r，因为P 为棱1CC上一点，所以)()01CP CC l l ==££uuu r uuuu r，所以(),BP BC CP =+=-+-uuur uuu r uuu r，设平面11AB D)11x r，则1111111100AB n AD n ì×=-+=ïí×=-=ïîuuur r uuuu r r ，令11x =可得平面11AB D 的一个法向量为()1,0,2n =r ，令0n BP×=-+=r uuu r解得23l =，故存在点P ，使得直线BP P 平面11AB D ，A 说法错误；当点P 与1C 重合时即P，)0,D -，(BP =-uuu r，()0,BD =-r，设平面则BP m BD m ì×ïí×ïîuuu r r uuu r r1可得平面BPD 的一个法向量为()1,0,1m =u r ，因为1CC =uuuu r 1^平面BPD ，B 说法正确；当P 为1CC，()AD =--uuu r，所以cos ，所以直线BP 与AD 所成角的余弦值为cos ,BP AD =uuu r C 说法正确；设正四棱台1111ABCD A B C D -的高为h ，当P 为1CC 三棱锥111A A B D -的体积111111122332A B D V S h ==´´´V 三棱锥P BCD -的体积2111443232BCD h V S ==´´´=V 所以三棱锥111A A B D -与三棱锥P BCD -的体积之比为1:2，D 说法正确；故选：BCD11．已知函数()(),f x g x 的定义域均为R ，()()112f x g x -++=，()()22g x f x --=，()()42g x f x --=，且当(]0,1x Î时．()21f x x =+，则（ ）A. ()20242g =B.20241()0i g i ==åC. 函数()f x 关于直线3x =对称D. 方程()2024f x x +=有且只在3个实根【答案】ACD【解析】对于A ：由()()()()11242f x g x g x f x ì-++=ïí--=ïî，可得()()()()2242f x g x g x f x ì+-=ïí--=ïî，所以(2)(4)4g x g x -+-=所以[2(2)][4(2)]4g x g x --+--=，即()(2)4g x g x ++=所以(2)(4)4g x g x +++=，得()(4)g x g x =+，故()g x 为周期函数，且周期为4，又()()()()11222f x g x g x f x ì-++=ïí--=ïî，可得()()()()2222f x g x g x f x ì+-=ïí+-=ïî，故(2)(2)4g x g x -++=，令0x =可得()22g =，令()(2)4g x g x ++=中的0x =可得()02g =所以()()202402g g ==，A 正确；对于B ：因为当(]0,1x Î时，()21f x x =+，所以()12f =，由()()112f x g x -++=得()()112f g +=，所以()10g =由()()42g x f x --=得()()312g f -=，所以()34g =，又()()402g g ==，所以()()()()()20241()506123450602424048i g i g g g g =éù=+++=´+++=ëûå，B 错误；对于C ：由()()()()11242f x g x g x f x ì-++=ïí--=ïî，可得()()()()2242f x g x g x f x ì-+=ïí--=ïî，故(2)(4)0f x f x -+-=，即(2)()f x f x +=-，(4)()f x f x +=，由()()()()11222f x g x g x f x ì-++=ïí--=ïî，可得()()()()112112f x g x g x f x ì-++=ïí+--=ïî，故(1)(1)0f x f x -+-=，即()()f x f x =--，所以()(2)()f x f x f x +=-=-故()f x 为奇函数，关于1x =对称，且周期为4，又当(]0,1x Î时．()21f x x =+，作出()f x 的图象如下：由图可知函数()f x 关于直线3x =对称，C 正确；对于D ：方程()2024f x x +=，即()f x x =，由图可知，函数()f x 的图象和y x =的图象有3个交点，即方程()2024f x x +=有3个实根，D 正确.故选：ACD.三、填空题：本题共3小题，每小题5分，共15分.12．甲、乙、丙、丁、戊五名同学利用寒假参加社区服务，分别从为老年人服务、社会保障服务、优抚对象服务、为残病人服务、安全防范服务等五个服务项目中选择一个报名，记事件A 为“五名同学所选项目各不相同”，事件B 为“只有甲同学选安全防范服务”，则()P A B =_________.【答案】332【解析】事件AB ：甲同学选安全防范服务且五名同学所选项目各不相同，所以其它4名同学排列在其它4个项目，且互不相同，为44A ，事件B ：甲同学选安全防范服务，所以其它4名同学排列在其它4个项目，可以安排在相同项目，为44，()()()44545A 354325P AB P A B P B ===.故答案为：332.13.已知0,4x p éùÎêúëû，sin cos x x +=，则 3 tan 4x p æö-=ç÷èø_________.【答案】3【解析】方法一：因为29(sin cos )12sin cos 5x x x x +=+=，所以sin cos x ，21(cos sin )12sin cos 5x x x x -=-=，因为0,4x p éùÎêúëû，所以cos sin x x -=3 tan 1sin cos tan 341tan cos sin x x x x x x x p ++æö-===ç÷--èø.方法二：由22sin sin cos 1x x x ìï++=íïî及0,4x p éùÎêúëû，解得sin cos x xìï==íïî所以1tan 2x =，113 tan 12tan 3.141tan 12x x x p ++æö-===ç÷-èø-故答案为：314.抛物线22(0)x py p =>与椭圆221(0)4x y m m +=>有相同的焦点，12,F F 分别是椭圆的上、下焦点，P 是椭圆上的任一点，I 是12PF F △的内心，PI 交y 轴于M ，且2PI IM =uu r uuu r ，点()()*,n n x y n ÎN 是抛物线上在第一象限的点，且在该点处的切线与x 轴的交点为()1,0n x +，若28x =，则2024x =____________．【答案】201912æöç÷èø【解析】22(0)x py p =>焦点在y 轴上，故椭圆221(0)4x ym m +=>的焦点在y 轴上，故4m >，I 是12PF F △的内心，连接2F I ，则2F I 平分12F F P Ð，在2PF I △中，由正弦定理得222sin sin PIPF PF I PIF =ÐÐ①，在2MF I V ，由正弦定理得222sin sin MI MF MF I MIF =ÐÐ②，其中22πMIF PIF Ð+Ð=，故22sin sin MIF PIF Ð=Ð，又22sin sin PF I MF I Ð=Ð，式子①与②相除得22PI PF MIMF =，故222PF MF =，同理可得112PI PF IMF M==，121222PF PF F M F M \+=+，由椭圆定义可知1224PF PF a +==，122F M F M c +=，24,1a c c \=\=，即焦点坐标为()0,1±，所以抛物线方程为24x y =，12y x ¢=，故24x y =在(),n n x y 处的切线方程为()12n n n y y x x x -=-，即21122n n n y y x x x -=-，又214n n y x =，故12n n y x x y =-，所以24x y =在点(),n n x y 的切线为：22n n x x y y =+，令212240,2nn n n n nx y x y x x x +´====，又1282x x ==，即116x =，所以{}n x 是首项16，公比12的等比数列，202320192024111622x æöæö\=´=ç÷ç÷èøèø．故答案为：201912æöç÷èø四、解答题：本题共5小题，共77分.解答应写出文字说明、证明过程或演算步骤.15．如图，在直四棱柱1111ABCD A B C D -中，BC CD ^，AB DC P ，12244DC BC CC AB ====．（1）证明：111AC B D ^；（2）求二面角11D B C D --【答案】（1）证明见解析 （2．【解析】（1）法一：连接11A C ，交11B D 于点H ，在梯形1111D C B A 中，111,A B =112B C =，114C D =，所以1111111112A B B C B C C D ==，又11111190A B C B C D Ð=Ð=°，所以111111~A B C B C D V V ，则111111B A C C B D Ð=Ð，因为11111190B A C A C B Ð+Ð=°，所以11111190C B D A C B Ð+Ð=°，则1190C HB Ð=°，即1111B D A C ^．直四棱柱1111ABCD A B C D -中，1AA ^平面1111D C B A ，因为11B D Ì平面1111D C B A ，所以111^B D AA ．因为1AA 、1AC Ì平面11AA C ，1111AA AC A Ç=，所以11B D ^平面11AA C ．因为1AC Ì平面11AA C ，所以111AC B D ^．法二：以{}1,,CD CB CC uuu r uuu r uuuu r为正交基底，建立如图所示的空间直角坐标系C xyz -，则()0,0,0C ，()4,0,0D ，()0,2,0B ，()1,2,0A ，()10,0,2C ，()14,0,2D ，()10,2,2B ，()11,2,2A ．的因为()11,2,2AC =--uuuu r ，()114,2,0B D =-uuuur，所以()()1111,2,24,2,04400AC B D ×=--×-=-++=uuuu r uuuur，所以111AC B D ^uuuu r uuuur，即111AC B D ^．（2）设平面1B CD 与平面11B CD 的一个法向量分别为()111,,m x y z =r 与()222,,n x y z =r，因为()10,2,2CB =uuur ，()14,0,2CD =uuuu r ，()4,0,0CD =uuu r，由1m CB m CD ì^ïí^ïîuuur r uuu r r 得111122040m CB y z m CD x ì×=+=ïí×==ïîuuur r uuur r ，则10x =，令11y =得11z =-，所以()0,1,1m =-r．由11n CB n CD ì^ïí^ïîuuur r uuuu r r 得122112220420n CB y z n CD x z ì×=+=ïí×=+=ïîuuur r uuuu r r ，令21x =，则12z =-，22y =，所以()1,2,2n =-r．所以cos ,m =r ，由图可知二面角11D B C D--所以二面角11D B C D --．16．某学校计划举办趣味投篮比赛，比赛分若干局进行.每一局比赛规则如下：两人组成一个小组，每人各投篮3次；若某选手投中次数多于未投中次数，则称该选手为“好投手”；若两人均为“好投手”，则称该小组为本局比赛的“神投手组合”.假定每位参赛选手均参加每一局的比赛，每人每次投篮结果互不影响.若甲､乙两位同学组成一个小组参赛，且甲､乙同学的投篮命中率分别为21,32.（1）求在一局比赛中甲被称为“好投手”的概率；（2）若以“甲､乙同学组成的小组获得“神投手组合”的局数为3的概率最大”作为决策依据，试推断本次投篮比赛设置的总局数()4n n ³为多少时，对该小组更有利？【答案】（1）2027（2）详见解析【解析】（1）设一局比赛中甲被称为好投手的事件为A ，则()233322222222122220C 1+C 3+133333333333327P A æö=×××-×××=××××××=ç÷èø；（2）设一局比赛中乙被称为好投手的事件为B ，则()23331111111111111C 1+C 3+12222222222222P B æö=×××-×××=××××××=ç÷èø，甲、乙同学都获得好投手的概率为：2011027227P =´=，比赛设置n 局，甲､乙同学组成的小组获得“神投手组合”的局数为X ，则10,27X B n æöç÷èø:，且()33310103C 12727n n P X -æöæö==-ç÷ç÷èøèø，设()3331=1010C 2727n nf n -æöæö-ç÷ç÷èøèø，则()()()()11f n f n f n f n ì³+ïí³-ïî，则 3332331333433110101010C 1C 12727272710101010C 1C 127272727n n n n n n n n --+---ìæöæöæöæö-³-ïç÷ç÷ç÷ç÷ïèøèøèøèøíæöæöæöæöï-³-ç÷ç÷ç÷ç÷ïèøèøèøèøî，即 ()17212717327n n n n ì-³+ïïíï³-ïî，即 7.18.1n n ³ìí£î，又 *N n Î，则 8n =，所以本次投篮比赛设置的总局数8时，对该小组更有利.17.设函数()ln (1)(2)f x x a x x =+--，其中a 为实数．（1）当1a =时，求()f x 的单调区间；（2）当()f x 在定义域内有两个不同的极值点12,x x 时，证明：()()1259ln 916f x f x +>+．【答案】（1）()f x 的单调递增区间为10,,(1,)2æö+¥ç÷èø，单调递减区间为1,12æöç÷èø （2）证明见解析【解析】（1）()f x 的定义域为(0,)+¥，21231()(23)x x f x x x x-+¢=+-=，令()()()2110x x f x x-¢-==，得12x =或1x =，10,(1,)2x ¥æöÎÈ+ç÷èø时，()0f x ¢>，1,12x æöÎç÷èø时，()0f x ¢<，所以()f x 的单调递增区间为10,,(1,)2¥æö+ç÷èø，单调递减区间为1,12æöç÷èø；（2）221(3)ax ax xf x -=¢+，由()f x 在(0,)+¥上有两个不同的极值点12,x x ，故22310ax ax -+=有两个不同的正根，则有1212220302102Δ980a x x x x aa a ¹ìïï+=>ïíï=>ïï=->î，解得89a >，因为()()()()()2212121212ln 34f x f x x x a x x a x x a+=++-++()()]()()2121212127ln 234ln 214x x a x x x x a x x a a a é=++--++=-+-ë，设7()ln(2)14g a a a =-+-，89a >，则7174()044a g a a a -¢=-=>，故()g a 在8,9¥æö+ç÷èø上单调递增，又816559()lnln 999916g a g æö>=-+=+ç÷èø，故()()1259ln 916f x f x +>+．18．设动点(),M x y与定点)2F的距离和它到定直线:l x =，记点M 的轨迹为曲线C ．（1）求曲线（2）设1(F 过点2F 的直线与C 的右支相交于A ，B 两点，I 是1F AB V 内一点，且满足111||||||0F B IA BA IF AF IB ×+×+×=uu r uur uu r r，试判断点I 是否在直线l 上，并说明理由．【答案】（1）221x y -= （2）点I 在直线l 上，理由见解析【解析】（1）由动点(,)M x y 与定点)2F 的距离和它到定直线:l x =，=，化简得221x y -=，故所求曲线C 的方程为221x y -=．（2）点I l 上．因为F ，设点,,I A B 的坐标分别是()()()1122,,,,,x y x y x y ，)()()122,,0,0x y AF x x y y -+--=，解得当AB 13,2A AB ==，代入有x ==，所以点I 在直线l 上，当AB 不与x 轴垂直时，设直线AB的方程是(y k x =，因为曲线C1±，且直线AB 与曲线C 的右支相交于两点，所以1k >，联立方程组(22y k x ì=ïí，整理得()()22221210k x x k -+-+=，)12x x+．()))11211212112F B x x x x x éù+--++ëû(()()11212122x x x x x x =++=-++222221111k k k k ö+-=+=++÷--ø所以x I 在直线l 上．.19．若无穷数列{}n a 的各项均为整数．且对于*,i j "ÎN ，i j <，都存在k j >，使得k j i j i a a a a a =--，则称数列{}n a 满足性质P ．（1）判断下列数列是否满足性质P ，并说明理由．①n a n =，1n =，2，3，…；②2n b n =+，1n =，2，3，…．（2）若数列{}n a 满足性质P ，且11a =，求证：集合{}*3n n a Î=N 为无限集；（3）若周期数列{}n a 满足性质P ，求数列{}n a 的通项公式．【答案】（1）数列{}n a 不满足性质P ；数列{}n b 满足性质P ，理由见解析 （2）证明见解析 （3）0n a =或3n a =．【解析】（1）对①，取1i =，对,1j j *"Î>N ，则11,j i j a a a ===，可得11j j i i j a a a j a =---=--，显然不存在,k j k *>ÎN ，使得1k a =-，所以数列{}n a 不满足性质P ；对②，对于,,i j i j *"Î<N ，则2i b i =+，2j b j =+，故()()()()2222j i i j i j i j i j i jb b b b --=++-+-+=×++()22i j i j =×++-+，因为,,1,2i j i j *γ³N ，则()2i j i j *×++-ÎN ，且()()2123i j i j i j j ×++-=++-³，所以存在()2k i j i j *=×++-ÎN ，k j >，使得()22j k i j i b b i b j i j b b =×++-=--+，故数列{}n b 满足性质P ；（2）若数列{}n a 满足性质P ，且11a =，则有：取111,1,i j j j *==>ÎN ，均存在111,k j k *>ÎN ，使得111111k j j a a a a a =--=-，取2121,,i j j k j *==>ÎN ，均存在2212,k j k k *>>ÎN ，使得222111k j j a a a a a =--=-，取121,i k j k k ==>，均存在1211,m k m *>>ÎN ，使得112123m k k k k a a a a a =--=，故数列{}n a 中存在n *ÎN ，使得3n a =，即{}3∣n n a *Î=¹ÆN ，反证：假设{}3∣n n a *Î=N 为有限集，其元素由小到大依次为()12,,,1l l n n n n >L ，取1,1l l i j n n ==+>，均存1,L l L k n k *>+ÎN ，使得11111L l l k n n a a a a a ++=--=-，取1,1L i j k ==+，均存在111,L L L k k k *++>+ÎN ，使得111111L L L k k k a a a a a +++=--=-，取1,L L i k j k +==，均存在111,l L l l n k n n *+++>>ÎN ，使得1113l L L L L n k k k k a a a a a +++=--=，即{}13∣l n n n a *+ÎÎ=N 这与假设相矛盾，故集合{}3∣n n a *Î=N 为无限集.（3）设周期数列{}n a 的周期为1,T T *³ÎN ，则对n *"ÎN ，均有n n T a a +=，设周期数列{}n a 的最大项为,,1M a M M T *Σ£N ，最小项为,,1N a N N T *Σ£N ，即对n *"ÎN ，均有N n M a a a ££，若数列{}n a 满足性质P ：反证：假设4M a ³时，取,i M j M T ==+，则,k M T k *$>+ÎN ，使得22k M M T M M T M M a a a a a a a ++=--=-，则()2330k M M M M M a a a a a a -=-=->，即k M a a >，这对n *"ÎN ，均有N n M a a a ££矛盾，假设不成立；则对n *"ÎN ，均有3n a £；反证：假设2N a £-时，取,i N j N T ==+，则,k N T k *$>+ÎN ，使得224k N N T N N T N N a a a a a a a ++=--=-³，在这与对n *"ÎN ，均有3n a £矛盾，假设不成立，即对n *"ÎN ，均有1n a ³-；综上所述：对n *"ÎN ，均有13n a -££，反证：假设1为数列{}n a 中的项，由（2）可得：1,3-为数列{}n a 中的项，∵()13135-´---=-，即5-为数列{}n a 中的项，这与对n *"ÎN ，均有13n a -££相矛盾，即对n *"ÎN ，均有1n a ¹，同理可证：1n a ¹-，∵n a ÎZ ，则{}0,2,3n a Î，当1T =时，即数列{}n a 为常数列时，设n a a =，故对,,i j i j *"Î<N ，都存在k j >，使得22i k i j j a a a a a a a a =--=-=，解得0a =或3a =，即0n a =或3n a =符合题意；当2T ³时，即数列{}n a 至少有两个不同项，则有：①当0,2为数列{}n a 中的项，则02022´--=-，即2-为数列{}n a 中的项，但{}20,2,3-Ï，不成立；②当0,3为数列{}n a 中的项，则03033´--=-，即3-为数列{}n a 中的项，但{}30,2,3-Ï，不成立；③当2,3为数列{}n a 中的项，则23231´--=，即1为数列{}n a 中的项，但{}10,2,3Ï，不成立；综上所述：0n a =或3n a =.。

2023年全国高考冲刺押题卷五语文作为即将迎来2023年高考的考生，你可能已经在为语文科目的备考做准备。

而在备考的过程中，押题卷往往是考生备考的重点之一。

2023年全国高考冲刺押题卷五语文也将成为备考的热门话题之一。

在本文中，我将从不同的角度为你解析这一主题，帮助你更全面、深入地了解备考的重要内容。

1. 高考冲刺押题卷的价值2023年全国高考冲刺押题卷五语文，作为备考的重要资料之一，具有很高的价值。

它包含了在备考过程中可能会遇到的各种类型题目，可以帮助考生更好地了解高考考题的出题规律和考点分布，进而有针对性地进行备考。

通过做冲刺押题卷，考生可以提前感受到高考的考试氛围和压力，更好地适应高考的考试要求。

2. 冲刺押题卷五的内容特点冲刺押题卷五语文的内容特点主要包括：综合性、灵活性和深度性。

它所涵盖的内容可能包括各种文体的阅读与鉴赏、古诗文鉴赏、现代文阅读、作文等多个方面。

对考生来说，要全面备考，就需要在综合性、灵活性和深度性三个方面都做好准备，这样才能应对冲刺押题卷五的考试。

3. 备考策略针对2023年全国高考冲刺押题卷五语文，考生在备考过程中要制定科学的备考策略。

要对押题卷的题型和考试要求进行全面的了解和分析，找准重点和难点，有针对性地进行备考。

可以通过做一些模拟题和真题来熟悉考试的形式和节奏，提高应试能力。

要注重平时的积累和阅读，提高语文素养和分析能力，为备考打下坚实的基础。

总结回顾通过对2023年全国高考冲刺押题卷五语文的全面评估和讨论，我们不仅对这一备考资料有了更深入的了解，也为备考制定了科学的备考策略。

正如备考语文一样，面对考试，要做的不仅是死记硬背，更需要全面、灵活和深入地准备，才能在考场上取得优异的成绩。

个人观点和理解对于备考2023年全国高考冲刺押题卷五语文，我个人认为，要注重平时的积累和阅读，培养对语文的兴趣和理解能力是非常重要的。

考生要多读一些名著、经典，多加练习写作，提高语文素养和应试能力，这样才能更好地备考语文，取得理想的成绩。