初中数学中的几个最值模型初探
- 格式:pdf
- 大小:127.03 KB
- 文档页数:2

动点最值问题永远都是中考最难的压轴类题目,很多同学都反应不知道该怎么下手寻找思路。
其实这类题目的题型有限,全部总结归纳就是这19种,希望同学们对每一种都能掌握技巧,再遇见类似的就能及时找到思路。
PS:可下载电子版打印高清版本,链接文末获取!
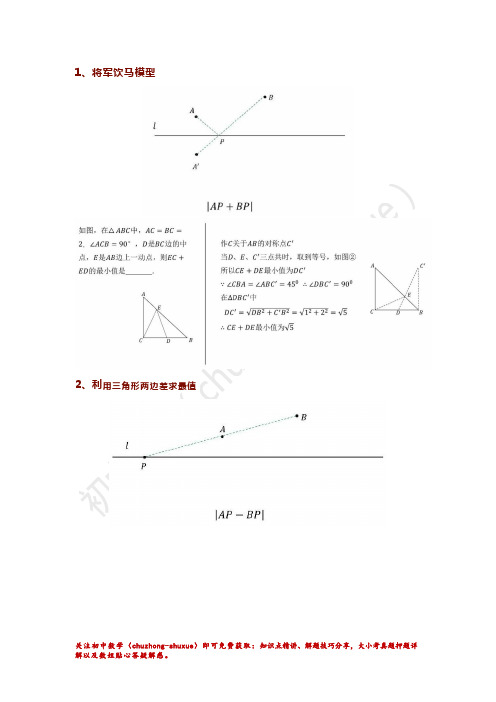
1、将军饮马模型(对称点模型)
2、利用三角形两边差求最值
3、手拉手全等取最值
4、手拉手相似取最值
5、平移构造平行四边形求最小
6、两点对称勺子型连接两端求最小
7、两点对称折线连两端求最小
8、时钟模型,中点两定边求最小值
9、时钟模型,相似两定边求最小值
10、转化构造两定边求最值
11、面积转化法求最值
12、相似转化法求最值
13、相似系数化一法求最值
14、三角函数化一求最值
15、轨迹最值
16、三动点的垂直三角形
17、旋转最值
18、隐圆最值-定角动弦
19、隐圆最值-动角定弦。

初中数学:最短路径求最值12个模型详解姓名: __________指导: ___________日期: __________初二数学最短路径问题【问题概述】最短路径问题是图论研究中的一个经典算法问题,旨在寻找图(由給点和路径组成的)中两结点之间的最短路径.算法具体的形式包括:①确定起,点的最短路径问题・即已知起始结点,求嚴短路径的问题.②确定终点的最短路径问题-与确定起点的问题相反,该问题是已知终结结点,求锻短路径的问题.③确定起点终点的最短路径问题・即已知起点和终点,求两结点之间的最短路径.④全局嚴短路径问题・求图中所有的最短路径.【问题原型】''将军饮马”,“造桥选址“,''费马点'、.【涉及知识】“两点之间线段最短“,“垂线段最短”,“三角形三边关系”,“轴对称”,“平移【岀题背景】角、三角形、菱形、矩形、正方形、梯形、圆、坐标轴、抛物线等.【解题思路】找对称点实现“折"转“直“,近两年出现“三折线”转“直"等变式问题考查.【例题及解析】例I 如图1,在直角梯形 A BCD 中,ZABC=90。
,AD〃BC, AD=4, AB=5, BC=6,点P是AB上一个动点.当PC + PD的和最小时,PB的收为( )(A)l (B)2 (C)2.5 (D)3DM D C图1分析此题首先要确定P点的位置,可以延长CB (或DA)的一倍,即CB=BM,再连接MD交AB于点P(大家可以思考一下P点的正确性与合理性一可运用两点之间,线段谥短这一性质〉.我们可以通过△MFBsADPA,从而求出FB的圮故选D.例2如图2, AABC中,AB = AC=I31 BC=10, AD是BC边上的中线,F为AD上的动点,E为AC边上的动点,则CE + EF的最小值为______ •分析显然,本题需要确定两个动点E和F,那么,怎样确定这两个点呢?我们可以过点B 作BE丄AC 交AD于点F,从而确定了E和卜点(大家可以用从直线外一点与直线上所有点的连线中,垂线段最短来加以说明).此时,CF + EF = BE.用S舛=• BC = -BE•祀■构逍方程■求出BE二罟.即CE七EF的艰小伉为罟.例3如图3,已知平面直角坐标系中,A (2, —3), B(4, —1)・(1) 若点卩仕,0)是x轴上的一个动点,当APAB的周长最短时,求x的值;(2) 若C、D是x轴上的两个动点,且D(a, 0), CD=3,当四边形ABCD的周长最短时, 求a的值;(3) 设M, N分别为x轴、y轴上的动点,问:是否存在这样的点M(m, 0)和N(0, n), 使得四边形ABMN的周长巌短?若存在,求岀n的值.若不徉在,请说明理由.分析与解(1)如图3,找岀A (或B)关于x轴的对称点Ai,连结AiB交x轴于点P・设直线AiB的解析式为y =kix+bi・将A】(2, 3)、B(4, -1)代入,得严:+ 6.仏+ 6, 解之码l k'=-2'16, =7. 故〉=-2x+7,(2)如图4,过A点作x轴的平行线,井戳取AA】=3・画点A,关于x轴的对称点A?,连结・dB交x紬于点C.再在x轴上截取「1) = 3,可得周长最短的四边形ABCD (大家也可以利用两点之间,线段最短,来证明最短周长的正确性).由题厳,町知4,(53).设A2B的直线解析式为y = k込4 by将人(5.3)出(4.・1)代人■得当时“殳八”3诗(3) 如图5t我们可以先分别找岀A、B关于y轴和x轴的对称点片和B b再连结AiB u分别交x袖和y轴于点M与N,此时,四边形ABMN的周长是最短的(同样, 可以用两点之间,线段最短来加以证明).设A I B I的直线解析式为y=bx + bs・将 4,(-2. -3) A(4.1)代入•得= 1 •1 ・ 2k 、+ by = - 3,2 5故 y = y * - y. 当 x = OHhy S -y,当y «0时/ •壬・ 所以・m.n 的值分别为手•■斗例4如图6,四边形ABCD 是正方形,M 是对角线BD 上的任意一点.(1)当点M 在何处时.AM+CM 的值最小?(2)当点M 在何处时,AM + BM + CM 的值最小?并说明理由.分析(1)(如图6,显然,连结AC 与BD 的交点即为M 点(可利用两点之间,线段最短来证明).⑵如图7,以AB 为边在正方形外画等边三角形ABE.连结EC 交BD 于点M ・此时, MA-I MB 4-MC-EC(M 中,A UMN 为等边三焦形,且 VEBN^ACBM,所以 MA I MB-EM). 若在BD 上(除N4点之外)任取一点卜1八过点Mi 作M1N1//MN 交BN 或延长线于点 连结ENi.可利用两点之间线段嚴短,证明MiA + M 】B+MK>EC,从而得岀MA+MB + Mca 短.解之得H s y-。

初中数学最值问题有六种模型,包括将军饮马模型、一箭穿心模型、费马点模型、阿氏圆模型、胡不归模型和瓜豆原理模型。
1. 将军饮马模型:当两定点A、B在直线l同侧时,在直线上找一点P,使PA+PB最小。
可以理解为两点之间线段最短。
连接AB交直线l于点P,点P即为所求作的点。
2. 一箭穿心模型:在直线l上找M、N两点(M在左),使得AM+MN+NB最小,且MN=d。
将点A向右平移d个单位到A′,作A′关于直线l的对称点A",连接A"B交直线l 于点N,将点N向左平移d个单位到M,点M、N即为所求。
3. 费马点模型:在三角形ABC中,若D、E分别是AB、AC 上的点,则DE的延长线与BC的延长线交于费马点处,此时三角形周长最小。
4. 阿氏圆模型:以给定点A为圆心,给定距离r为半径画圆,与已知直线l相交于两点B、C,连接两点B、C并延长交于D。
则D点的轨迹是以A为圆心,r为半径的圆。
这个圆被称为阿氏圆。
5. 胡不归模型:在直角三角形ABC中,AB=c,AC=b,BC=a,AD为BC边上的高。
若点P在BC边上,问是否存在点P使得DP垂直于BC边?如果存在,求出点P的位置;
如果不存在,请说明理由。
6. 瓜豆原理模型:在一条直线上有若干个点,每个点都有一个到直线的距离,问如何选择若干个点使得这些点到直线的距离之和最小?瓜豆原理告诉我们,选择任意两个相邻的点并连接它们与直线的交点,然后选择第三个点与前两个点的距离之和最小即可。
以上是初中数学最值问题的六种模型,希望对解决这类问题有所帮助。

专题01绝对值中的四类最值模型最值问题一直都是初中数学中的最难点,但也是高分的必须突破点,而绝对值中的最值模型是初中学生第一次接触最值类问题,该类最值模型解题的主要依据是绝对值的几何意义或代数意义。
本专题就绝对值中的四种最值模型进行梳理及对应试题分析,方便大家掌握。
绝对值的性质:①正数的绝对值是它本身,即a a =;②0的绝对值是0,即00=;③负数的绝对值是它的相反数,即a a -=;④绝对值具有非负性,即0≥a 。
模型1.b x a x -+-的最小值模型【模型解读】式子b x a x -+-在b x a ≤≤时,取得最小值为b a -。
【最值原理】b x a x -+-目的是在数轴上找一点x ,使x 到a 和b 的距离和的最小值:另解:也可用绝对值的代数意义(即分类讨论思想)完成绝对值的最值问题。
例1.(2023·广东七年级期中)阅读下面材料:数轴是数形结合思想的产物.有了数轴以后,可以用数轴上的点直观地表示实数,这样就建立起了“数”与“形”之间的联系.在数轴上,若点A ,B 分别表示数a ,b ,则A ,B 两点之间的距离为AB a b =-.反之,可以理解式子3x -的几何意义是数轴上表示实数x 与实数3两点之间的距离.则当25x x ++-有最小值时,x 的取值范围是()A .2x <-或5x >B .2x -≤或5x ≥C .25x -<<D .25x -≤≤【答案】D【分析】根据题意将25x x ++-可以理解为数轴上表示实数x 与实数-2的距离,实数x 与实数5的距离,两者的和,分三种情况分别化简,根据解答即可得到答案.【解析】方法1:几何法(根据绝对值的几何意义)25x x ++-可以理解为数轴上表示实数x 与实数-2的距离,实数x 与实数5的距离,两者的和,通过数轴分析反现当25x -≤≤时,25x x ++-有最小值,最小值为7。
故选:D.方法2:代数法(借助零点分类讨论)当x <-2时,25x x ++-=(-2-x )+(5-x )=3-2x ;当25x -≤≤时,25x x ++-=(x +2)+(5-x )=7;当x >5时,25x x ++-=(x +2)+(x -5)=2x -3;∴25x x ++-有最小值,最小值为7,此时25x -≤≤,故选:D.【点睛】此题考查依据绝对值的性质化简绝对值,正确理解题意,得到25x x ++-表示的意义,再利用分类思想解答问题.①如图2,点A、B都在原点的右边:∣AB∣=∣OB∣-∣OA∣=∣b∣-∣a∣=b-a=∣a-b∣;②如图3,点A、B都在原点的左边:∣AB∣=∣OB∣-∣OA∣=∣b∣-∣a∣=-b-(-a)=∣a③如图4,点A、B在原点的两边:∣AB∣=∣OA∣+∣OB∣=∣a∣+∣b∣=a+(-b)=∣a-b【知识迁移】(1)点A,B表示的数分别是-(2)如图2,若点A,B表示的数分别是x,1的距离,得出当模型2.b x a x ---的最小值和最大值模型【模型解读】式子b x a x ---在a x ≤时,取得最小值为b a --;在b x ≥时,取得最大值b a -。

初三最值问题的常用解法及模型一、引言初三数学中最值问题一直是学生们头疼的难题。
最值问题不仅仅是考察学生对知识点的掌握程度,更重要的是考验学生解决实际问题和推理的能力。
在本文中,我们将探讨初三数学中最值问题的常用解法及模型,帮助学生们更好地理解和应对这一难点。
二、常用解法1. 图形法最值问题常常可以通过图形法来解决。
给定一个函数y = f(x),可以通过画出其图像,然后找出函数的极值点来求解最值问题。
通过观察图像的特点,我们可以更直观地理解函数的最值点在何处,从而得到更准确的解。
2. 性质法有些最值问题可以通过利用函数的性质来解决。
关于一元二次函数的最值问题,我们可以通过一元二次函数的性质,如开口方向、顶点位置等来推导出最值点的位置,从而得到解的方法。
3. 等式法有些最值问题可以通过建立方程或不等式来解决。
通过建立关于未知数的方程或者不等式,我们可以将最值问题转化为解方程或解不等式的问题,从而得到最值点的位置。
三、常用模型1. 长方形面积最大问题给定一段定长的绳子,用这段绳子围成一个长方形,求这个长方形的面积最大是一个最值问题。
通过建立关于长方形面积的函数,然后利用导数的性质找出函数的最值点,从而求解长方形面积最大问题。
2. 等边三角形周长最小问题给定一个定长的线段,求能够围成等边三角形的线段最小是一个常见的最值问题。
通过建立关于等边三角形周长的函数,然后利用导数的性质找出函数的最值点,从而求解等边三角形周长最小问题。
3. 盒子体积最大问题给定一定面积的纸张,通过剪切和折叠,能够制成一个盒子,求使得盒子体积最大的折法是一个典型的最值问题。
通过建立关于盒子体积的函数,然后利用导数的性质找出函数的最值点,从而求解盒子体积最大问题。
四、个人观点和理解最值问题在初三数学中是一个重要的难点,但也是一个可以锻炼学生逻辑思维能力和数学推理能力的好机会。
通过多维度的解法和模型,学生们可以更好地理解和掌握最值问题的解法,并且能够将数学知识与实际问题相结合,培养出更强的数学建模能力。
中考数学经典几何模型:最值类型一“将军饮马”模型通过对称进行等量代换,转化成两点之间的距离或点到直线的距离,或利用三角形两边之和大于第三边,两边之差小于第三边求得最值。
1、同侧、异侧两线段之和最短2、同侧、异侧两线段之差最大、最小例1:已知A. B. C. D四点如图所示,请画出一点P,使P到点A. B. C. D的距离之和最小,并说明理由。
简答:连接AD、BC,令其交点为P,在线段BC上任取一点Q(不同于点P),连接AQ、DQ,如图所示。
∵点P,点Q均在线段BC上,∴PB+PC=QB+QC,∵点P在线段AD上,∴PA+PD=AD,在△QAD中,QA+QDAD(两边之和大于第三边),即QA+QB+QC+QDPA+PB+PC+PD.∴线段AD、BC的交点P为所要找的点。
例2:如图:A,B两点在直线的两侧,点A到直线的距离AM=4,点B到直线的距离BN=2,且MN=4,P为直线上的动点,PA+PB的最小值为,|PA−PB|的最大值为,|PA−PB|的最小值为。
简答:(1)连接AB,交MN于点P,此时PA+PB最小=2√13(2)作B点关于MN的对称点B′,连接AB′并延长,与直线MN交于点P,此时|PA−PB|的值最大=PA-PB′=AB′=2√5理由:在直线MN上任找异于点P的一点P′,连接P′A,P′B′由三角形两边之差小于第三边可知,P′A-P′B≤AB′,当A、B′、P′三点共线时,取得最值(3)易知:在直线MN上存在一点P,使得PA=PB,此时|PA−PB|的值最小为03、三角形、四边形周长最小例1:如图,在四边形ABCD中,∠BAD=110∘,∠B=∠D=90∘.在BC,CD上分别找一点M,N,使△AMN周长最小,则∠AMN+∠ANM的度数为.解答:如图,作点A关于BC的对称点A′,关于CD的对称点A″,连接A′A″与BC、CD的交点即为所求的点M、N,∵∠BAD=110∘,∠B=∠D=90°,∴∠A′+∠A″=180°−110°=70°,由轴对称的性质得:∠A′=∠A′AM,∠A″=∠A″AN,∴∠AMN+∠ANM=2(∠A′+∠A″)=2×70°=140°.例2:如图,∠MON=20°,A、B分别为射线OM、ON上两定点,且OA=2,OB=4,点P、Q分别为射线OM、ON两动点,当P、Q运动时,线段AQ+PQ+PB的最小值是解答:作A关于ON的对称点A′,点B关于OM的对称点B′,连接A′B′,交于OM,ON分别为P,Q,连接OA′,OB′,则PB′=PB,AQ=A′Q,OA′=OA=2,OB′=OB=4,∠MOB′=∠NOA′=∠MON=20°,∴AQ+PQ+PB=A′Q+PQ+PB′=A′B′,∠A′OB′=60°,∵cos60°=1/2,OA′/OB′=1/2,∴∠OA′B′=90°,∴A′B′=2√3,∴线段AQ+PQ+PB的最小值是:2√3.4、需要平移的“将军饮马”例题:如图,已知四边形ABCD四个顶点的坐标为A(1,3),B(m,0),C(m+2,0),D(5,1),当四边形ABCD的周长最小时,m的值为______.解答:将C点向左平移2单位与B重合,点D向左平移2单位到D′(3,1),作D′关于x轴的对称点D″,则点D″(3,−1),设直线AD″的解析式为y=kx+b,带入A、D″两点坐标,解得k=−2,b=5.∴直线AD″的解析式为y=−2x+5.当y=0时,x=5/2,即B(5/2,0),∴m=5/2.5、点到直线垂线段最短例1:如图,在菱形ABCD中,AB=6,∠B=60∘,点G是边CD边的中点,点E. F分别是AG、AD上的两个动点,则EF+ED的最小值是.解答:如图作DH⊥AC垂足为H与AG交于点E,∵四边形ABCD是菱形,∵AB=AD=CD=BC=6,∵∠B=60°,∴∠ADC=∠B=60°,∴△ADC是等边三角形,∵AG是中线,∴∠GAD=∠GAC∴点H关于AG的对称点F在AD上,此时EF+ED最小=DH.∴EF+DE的最小值=DH=3√3例2:如图,矩形ABCD中,AD=5,AB=12,点M在AC上,点N在AB上,则BM+MN的最小值为( )简答:作B点关于AC的对称点E点,过E作EF垂直AB交AB于F点,AC=13,AC边上的高为60/13,所以BE=120/13.∵△ABC∽△BEF,∴AB/EF=AC/BE,求得EF=1440/169.类型二由已知定长线段求最值找到与所求最值相关成三角形的两个定长线段,定长线段的和为最大值,定长线段的差为最小值。
初三数学最值问题模型数学中的最值问题是非常经典的数学问题之一,初三学生也需要掌握这一基本知识。
下面,我将为大家介绍初三数学中的最值问题模型。
一、最大值问题最大值问题是指,在所有条件下使某一问题要求的数值最大的数,即为该问题的最大值。
初三数学中最大值问题多表现为以下几种:1.1 一次函数最大值问题一次函数可以表示为y = kx + b的形式,其中k为斜率,b为截距。
最大值问题就是要让y最大。
解题步骤:(1)求出y的表达式,设最大值点为(x0,y0)(2)化简y的表达式,得出x0的值(3)将x0的值带入y的表达式,得出y0的值(4)最大值为(y0, x0)1.2 二次函数最大值问题二次函数一般可以写成 y = ax^2 + bx + c 的形式。
指数为 2 的函数图像是一个抛物线,有一个最值点。
求二次函数的最大值就是求最值点。
解题步骤:(1)求出函数的导函数(2)将函数的导函数等于 0,求得所有的极值点(3)求出函数在每个极值点的函数值(4)最大值就是所有函数值中最大的一个1.3 正比例函数最大值问题正比例函数可以表示为 y = kx ,其中k为比例常数。
最大值问题就是要让y最大。
解题步骤:(1)求出y的表达式,设最大值点为(x0,y0)(2)化简y的表达式,得出x0的值(3)将x0的值带入y的表达式,得出y0的值(4)最大值为(y0, x0)1.4 平方差最大值问题平方差最大值问题是指,已知两个实数a和b,在满足a+b=k(k为常数)的条件下,使(a-b)的平方最大。
该问题也可以通过求导的方法解决。
二、最小值问题最小值问题与最大值问题非常相似,只是将最大值的条件改为最小值。
2.1 一次函数最小值问题解题步骤与一次函数最大值问题类似。
2.2 二次函数最小值问题解题步骤与二次函数最大值问题类似。
2.3 反比例函数最小值问题反比例函数可以表示为 y = k/x ,其中k为比例常数。
最小值问题就是要让y最小。