最新初中数学几个常用模型
- 格式:doc
- 大小:1.25 MB
- 文档页数:18
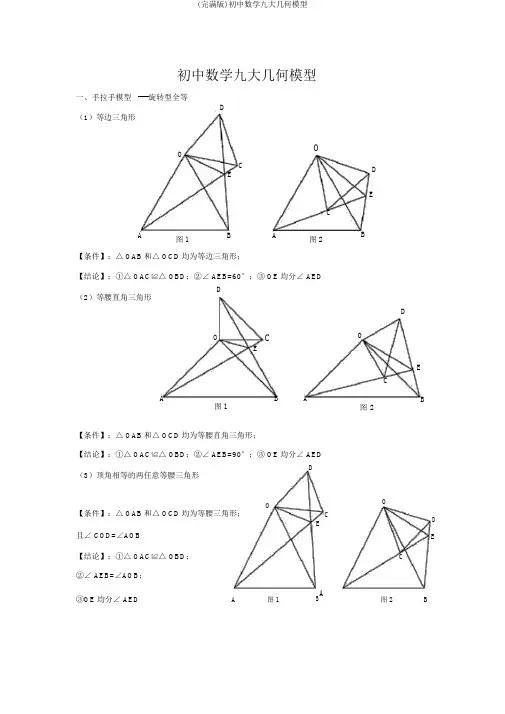
初中数学九大几何模型一、手拉手模型 ----旋转型全等D(1)等边三角形OOC ECA图 1BA图 2【条件】:△ OAB 和△ OCD 均为等边三角形;【结论】:①△ OAC ≌△ OBD ;②∠ AEB=60°;③ OE 均分∠ AEDD(2)等腰直角三角形OCEABA图 1D EBDOECB图 2【条件】:△ OAB 和△ OCD 均为等腰直角三角形;【结论】:①△ OAC ≌△ OBD ;②∠ AEB=90°;③ OE 均分∠ AED(3)顶角相等的两任意等腰三角形DOOC【条件】:△ OAB 和△ OCD 均为等腰三角形;DE且∠ COD=∠AOBE【结论】:①△ OAC ≌△ OBD ; C②∠ AEB=∠AOB ;③OE 均分∠ AEDA 图 1BA图 2 BO O二、模型二:手拉手模型----旋转型相似(1)一般情况D【条件】: CD ∥ AB ,CD将△ OCD 旋转至右图的地址A B 【结论】:①右图中△ OCD ∽△ OAB →→→△ OAC ∽△ OBD ;②延长 AC 交 BD 于点 E ,必有∠ BEC=∠ BOAO(2)特别情况C D【条件】:CD ∥ AB ,∠ AOB=90°将△ OCD 旋转至右图的地址A B【结论】:①右图中△ OCD ∽△ OAB →→→△ OAC ∽△ OBD ; ②延长 AC 交 BD 于点 E ,必有∠ BEC=∠ BOA ;③ BDOD OB tan ∠ OCD ;④ BD ⊥AC ; ACOC OA⑤连接 AD 、 BC ,必有 AD 2BC222;⑥ S △BCDABCD三、模型三、对角互补模型(1)全等型 -90 °【条件】:①∠ AOB=∠ DCE=90°;② OC 均分∠ AOBECABDOCEA B1AC BD 2 ACDOE B图 1【结论】:① CD=CE ;② OD+OE= 2 OC ;③ S △DCES△OCDS△OCE1 OC 2A2证明提示:CM①作垂直,如图 2,证明△ CDM ≌△ CEND②过点 C 作 CF ⊥ OC ,如图 3,证明△ ODC ≌△ FEC※当∠ DCE 的一边交 AO 的延长线于 D 时(如图 4):ON EB图 2以上三个结论:① CD=CE ;② OE-OD= 2 OC ;A1OC 2AMC③S△OCES△OCD2CDONBEO图 3 EF BD图 4(2)全等型 -120 °【条件】:①∠ AOB=2∠ DCE=120°;② OC均分∠ AOB【结论】:① CD=CE;② OD+OE=OC;③S△DCE S△OCD S△OCE 3 OC24证明提示:①可参照“全等型-90 °”证法一;②如右以下图:在OB上取一点F,使 OF=OC,证明△ OCF为等边三角形。

初中常见数学模型几何和证明方法初中数学中的几何和证明方法是学习数学的重要内容之一。
通过几何学习,学生可以掌握基本的几何概念、性质和定理,进而培养逻辑思维、分析问题和解决问题的能力。
而证明方法则是通过推理和论证的方式验证和证明数学命题的正确性。
下面将对初中常见的几何模型和证明方法进行介绍。
一、几何模型1. 点、线、面:几何学的基本要素是点、线和面。
点是没有大小和形状的,用来表示位置;线是由无数个点组成的,它没有宽度和厚度;面是由无数个线组成的,它有宽度和厚度。
2. 直线和线段:直线是由无数个点组成的,它没有起点和终点;线段是直线的一部分,有起点和终点。
3. 角:角是由两条射线共同起点组成的,可以用度数来表示。
4. 三角形:三角形是由三条线段组成的,它有三个顶点、三条边和三个角。
5. 直角三角形:直角三角形是一个角为90度的三角形,其中的两条边相互垂直。
6. 平行四边形:平行四边形是四边形的一种,它的对边是平行的。
7. 圆:圆是由一个固定点到平面上所有到该点距离相等的点组成的图形。
以上是初中常见的几何模型,通过对这些模型的学习,可以帮助学生理解几何概念和性质,为后续的学习打下基础。
二、证明方法1. 直接证明法:直接证明法是通过一系列逻辑推理,从已知条件出发,推导出结论的过程。
这种证明方法通常可以通过图形、等式等形式来进行。
2. 反证法:反证法是通过假设所要证明的命题不成立,然后通过逻辑推理,推导出一个与已知条件矛盾的结论,从而证明原命题的正确性。
3. 数学归纳法:数学归纳法是通过证明当命题对于某个特定的数成立时,对于下一个数也成立,进而可以推导出对于所有数都成立的结论。
这种证明方法常用于证明与自然数相关的命题。
4. 反证法:反证法是通过假设所要证明的命题不成立,然后通过逻辑推理,推导出一个与已知条件矛盾的结论,从而证明原命题的正确性。
5. 用反证法证明:用反证法证明是指通过假设所要证明的命题不成立,然后推导出一个与已知条件矛盾的结论,从而证明原命题的正确性。

以下是初二上册数学中常见的几何模型:
1. 三角形模型:用于研究三角形中的各种关系和定理,例如三角形的全等、相似和角平分线等。
2. 平行四边形模型:用于研究平行四边形的性质和判定,例如对角线相等、对角线互相平分等。
3. 矩形模型:用于研究矩形的性质和判定,例如四个角都是直角、对角线相等且互相平分等。
4. 菱形模型:用于研究菱形的性质和判定,例如四边相等、对角线互相垂直且平分等。
5. 勾股定理模型:用于研究勾股定理的证明和应用,例如直角三角形的三边关系等。
6. 圆模型:用于研究圆的性质和判定,例如圆周角定理、切线的判定和性质等。
7. 扇形模型:用于研究扇形的性质和面积计算,例如扇形的弧长和面积公式等。
8. 角平分线模型:用于研究角平分线的性质和判定,例如角的平分线与对边的关系等。
9. 中位线模型:用于研究中位线的性质和判定,例如中位线的长度等于它所截两边的平均值等。
10. 直角三角形模型:用于研究直角三角形的性质和判定,例如勾股定理的逆定理、直角三角形斜边的中线等于斜边的一半等。
以上是初二上册数学中常见的几何模型,掌握这些模型对于解决几何问题非常重要。
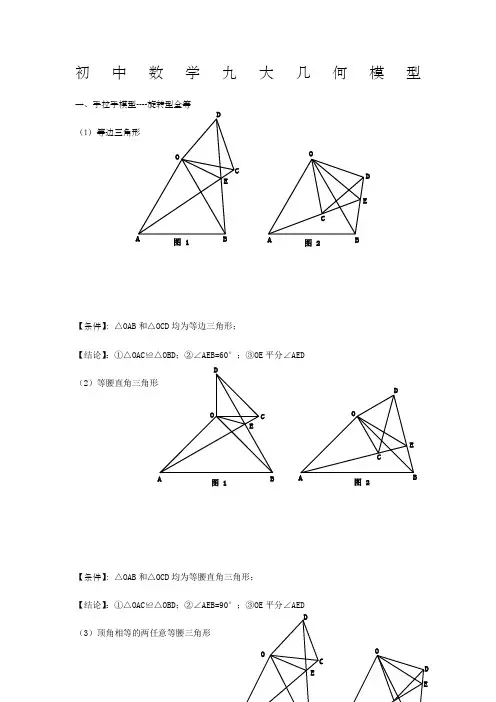
初中数学九大几何模型一、手拉手模型----旋转型全等 (1)等边三角形【条件】:△OAB 和△OCD 均为等边三角形;【结论】:①△OAC ≌△OBD ;②∠AEB=60°;③OE 平分∠AED(2)等腰直角三角形【条件】:△OAB 和△OCD 均为等腰直角三角形;【结论】:①△OAC ≌△OBD ;②∠AEB=90°;③OE 平分∠AED(3)顶角相等的两任意等腰三角形OB C DE图 1OABCD E图 2OABCDE图 1OACDE图 2OCDEOD E【条件】:△OAB 和△OCD 均为等腰三角形; 且∠COD=∠AOB【结论】:①△OAC ≌△OBD ; ②∠AEB=∠AOB ; ③OE 平分∠AED二、模型二:手拉手模型----旋转型相似 (1)一般情况【条件】:CD ∥AB , 将△OCD 旋转至右图的位置【结论】:①右图中△OCD ∽△OAB →→→△OAC ∽△OBD ; ②延长AC 交BD 于点E ,必有∠BEC=∠BOA (2)特殊情况【条件】:CD ∥AB ,∠AOB=90° 将△OCD 旋转至右图的位置【结论】:①右图中△OCD ∽△OAB →→→△OAC ∽△OBD ; ②延长AC 交BD 于点E ,必有∠BEC=∠BOA ;OAB COBCDEOB CDEOA CD③===OAOBOC OD AC BD tan ∠OCD ;④BD ⊥AC ; ⑤连接AD 、BC ,必有2222CD AB B C AD +=+;⑥BD AC 21S △BCD ⨯=三、模型三、对角互补模型 (1)全等型-90°【条件】:①∠AOB=∠DCE=90°;②OC 平分∠AOB【结论】:①CD=CE ;②OD+OE=2OC ;③2△OCE △OCD △DCE OC 21S S S =+= 证明提示:①作垂直,如图2,证明△CDM ≌△CEN②过点C 作CF ⊥OC ,如图3,证明△ODC ≌△FEC ※当∠DCE 的一边交AO 的延长线于D 时(如图4): 以上三个结论:①CD=CE ;②OE-OD=2OC ;③2△OCD △OCE OC 21S S =-(2)全等型-120°【条件】:①∠AOB=2∠DCE=120°;②OC 平分∠AOB【结论】:①CD=CE ;②OD+OE=OC ;③2△OCE △OCD △DCE OC 43S S S =+=AOBCDE 图 1A OBCDEM N图 2A OBCDEF图 3A O BCDEMN 图 4证明提示:①可参考“全等型-90°”证法一;②如右下图:在OB 上取一点F ,使OF=OC ,证明△OCF 为等边三角形。

初一数学几何模型
初一数学几何模型可以包括以下几个方面:
1. 平面几何模型:如平面上的点、线、角的模型;
2. 空间几何模型:如三维空间中的点、线、面、体的模型;
3. 图形的模型:如正方形、矩形、三角形、圆等图形的模型;
4. 图形的变换模型:如平移、旋转、镜像、放缩等图形的变换模型;
5. 相似与全等模型:如相似图形和全等图形的模型;
6. 坐标系与直角坐标系模型:如在平面上建立坐标系,进行坐标计算的模型;
7. 三角形的模型:如直角三角形、等腰三角形、等边三角形等模型;
8. 圆的模型:如圆的构造、圆的性质等模型;
9. 三视图模型:如立体图形的正视图、侧视图、俯视图等模型。
以上是初一数学几何模型的一些例子,通过这些模型可以帮助学生更好地理解和应用几何知识。
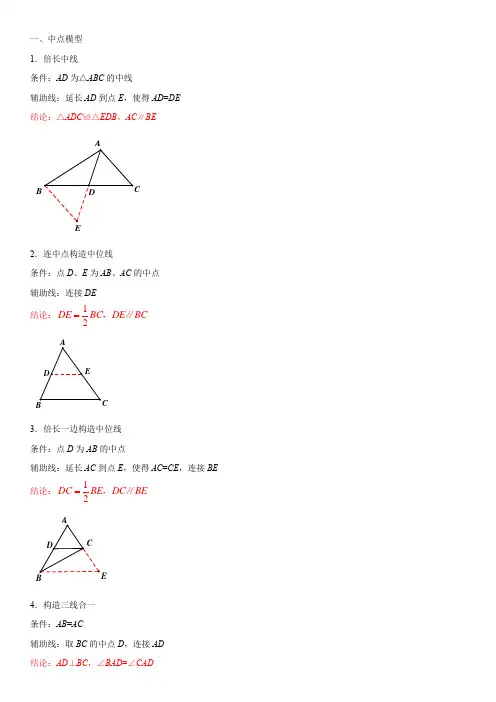
一、中点模型1.倍长中线条件:AD 为△ABC 的中线辅助线:延长AD 到点E ,使得AD =DE结论:△ADC ≌△EDB ,AC ∥BE2.连中点构造中位线条件:点D 、E 为AB 、AC 的中点辅助线:连接DE 结论:12DE BC DE BC =,∥3.倍长一边构造中位线条件:点D 为AB 的中点辅助线:延长AC 到点E ,使得AC =CE ,连接BE 结论:12DC BE DC BE =,∥4.构造三线合一条件:AB =AC辅助线:取BC 的中点D ,连接AD结论:AD ⊥BC ,∠BAD =∠CADB5.构造斜边中线条件:∠ABC =90°辅助线:取AC 的中点D ,连接BD 结论:12BD AC AD CD ===二、角平分线模型6.往角两边作垂线条件:AD 平分∠BAC辅助线:过点D 作AB 、AC 的垂线,垂足分别为E 、F结论:△ADE ≌△ADF7.在角的两边截取等长线段条件:AD 平分∠BAC辅助线:在AB 、AC 上取点E 、F ,满足AE =AF ,连接DE 、DF 结论:△ADE ≌△ADF8.过角平分线上一点作垂线条件:AD 平分∠BAC辅助线:过点D 作EF ⊥AD ,交AB 、AC 于点E 、FD CBB CCC结论:△ADE ≌△ADF三、双角平分线模型9.内内模型条件:BD 、CD 平分∠ABC 、∠ACB 结论:1902D A ∠=︒+∠10.内外模型条件:BD 、CD 平分∠ABC 、∠ACE 结论:12D A ∠=∠11.外外模型条件:BD 、CD 平分∠CBE 、∠BCF 结论:1902D A ∠=︒-∠四、平行线模型12.猪蹄模型CA BCC ED条件:AB ∥CD辅助线:过点E 作EF ∥AB结论:∠B +∠D =∠BED13.铅笔头模型条件:AB ∥CD辅助线:过点E 作EF ∥AB结论:∠B +∠D +∠BED =360°14.鸟头模型条件:AB ∥CD辅助线:过点E 作EF ∥AB结论:∠D +∠BED =∠B15.平行线+角平分线模型条件:AB ∥CD ,CE 平分∠ACD结论:AC =AE五、等积模型16.等底等高条件:AD ∥BCFAFBC结论:ABC DBC S S =,ADB ADC S S =17.等高模型条件:B 、C 、D 共线结论:::ABD ADC S S BD CD =18.等底模型条件:AE 、DE 为△ABC 、△DBC 边BC 上的高结论:::ABC DBC S S AE DE =六、对称半角模型19.对称半角模型-含45°角的三角形条件:∠BAC =45°,AD ⊥BC辅助线:作点D 关于AB 的对称点E ,关于AC 的对称点F , 连接AE 、AF 、BE 、CF 、EF结论:△AEF 是等腰直角三角形20.对称半角模型-含30°角的三角形B CB C DED条件:∠BAC =30°,AD ⊥BC辅助线:作点D 关于AB 的对称点E ,关于AC 的对称点F , 连接AE 、AF 、BE 、CF 、EF结论:△AEF 是等边三角形七、旋转半角模型21.旋转半角模型-等腰直角三角形条件:AB =AC ,∠BAC =90°,∠MAN =45°辅助线:将△ABM 绕点A 逆时针旋转90°,得到△ACM ' 结论:ANM ANM '≌,222BM CN MN +=22.旋转半角模型-等边三角形条件:△ABC 是等边三角形,BD =CD ,∠BDC =120°, ∠MDN =60°辅助线:将△BDM 绕点D 顺时针旋转120°,得到△DCM ' 结论:NDM NDM '≌,BM CN MN +=23.旋转半角模型-正方形条件:正方形ABCD ,∠MAN =45°,FEAM'M CAB辅助线:将△ABM 绕点A 逆时针旋转90°,得到△ADM ' 结论:NAM NAM '≌,BM DN MN +=八、自旋转模型24.自旋转模型-等边三角形条件:△ABC 是等边三角形,点P 为其内任意一点辅助线:将△BAP 绕点B 顺时针旋转60°,得到△BCP ' 结论:△BPP '是等边三角形25.自旋转模型-等腰直角三角形条件:△ABC 中,∠BAC =90°,AB =AC ,点P 为△ABC 内任 意一点辅助线:将△BAP 绕点A 逆时针旋转90°,得到△ACP ' 结论:△APP '是等腰直角三角形26.自旋转模型-等腰三角形条件:△ABC 中,AB =AC ,点P 为△ABC 内任意一点,∠BAC =α 辅助线:将△BAP 绕点A 逆时针旋转α,得到△ACP ' 结论:△APP '是等腰三角形M'DNCBAB九、手拉手模型29.手拉手模型-等边三角形条件:△ABC和△CDE都是等边三角形结论:△ACE≌△BCD27.手拉手模型-等腰直角三角形条件:△ABC和△CDE都是等腰直角三角形结论:△ACE≌△BCD,AE⊥BDEE28.手拉手模型-等腰三角形条件:△ABC 和△CDE 都是等腰三角形,CA =CB , CD =CE ,且∠ACB =∠DCE结论:△ACE ≌△BCD30.手拉手模型-正方形条件:四边形ABCD 和AEFH 都是正方形结论:△ABE ≌△ADH ,BE ⊥DH十、最短路程模型31.直线同侧两线段之和最小(将军饮马)条件:点A 、B 在直线l 同侧,点P 为l 上一点辅助线:作点A 关于直线l 的对称点A ',连接A 'B 结论:点P 为A 'B 和l 交点时,AP +BP 最小C32.直线异侧两线段之差最小条件:点A 、B 在直线l 异侧,点P 为l 上一点辅助线:作线段AB 的垂直平分线m结论:点P 为m 和l 交点时,|AP -BP |最小33.直线同侧两线段之差最小条件:点A 、B 在直线l 同侧,点P 为l 上一点辅助线:作线段AB 的垂直平分线m结论:点P 为m 和l 交点时,|AP -BP |最小34.过桥模型(将军饮马)条件:A 、B 为定点,l 1∥l 2,MN 为定长线段且MN ⊥l 1 辅助线:将点A 向上平移MN 的长度得到A ',连接A 'B 结论:点N 为A 'B 与l 1交点时,AM +MN +BN 最小35.四边形周长最小(将军饮马)条件:A 、B 为定点,M 、N 为角两边上的动点辅助线:作点A 、B 关于角两边的对称点A '、B ',连接 lAlAll 1l 2A'B'结论:M、N为A'B'与角两边交点时,四边形ABMN的周长最小B'36.三角形周长最小(将军饮马)条件:A为定点,B、C为角两边上的动点辅助线:作点A关于角两边的对称点A'、A",连接A'A"结论:B、C为A'A"与角两边交点时,△ABC的周长最小37.旋转类最短路程模型条件:线段OA=a,OB=b(a>b),OB绕点O在平面内旋转结论:点B与点N重合时,AB最小;点B与点M重合时,AB最大十一、基本相似模型38.A字型条件:BC∥DE结论:△ABC∽△ADE条件:∠ABC =∠ADE结论:△ABC ∽△ADE39.8字型条件:AB ∥CD结论:△AOB ∽△DOC条件:∠BAO =∠DCO结论:△AOB ∽△COD40.母子型条件:△ABC 中,∠ACB =90°,CD ⊥AB结论:△ABC ∽△ACD ∽△CBD41.一线三等角模型条件:∠B =∠D =∠ACE结论:△ABC ∽△CDECBCC A42.手拉手相似模型条件:△ABC ∽△ADE结论:△ACE ∽△ABD十二、对角互补模型43.对角互补模型-90°全等型条件:∠AOB =∠DCE =90°,OC 平分∠AOB辅助线:过点C 作CM ⊥AO ,CN ⊥BO ,垂足分别为M 、N 结论:△CDM ≌△CEN ,CD =CE ,OD +OEOC ,212OECD S OC 四边形CB ACE AB D CDD44.对角互补模型-120°全等型条件:∠AOB =120°,∠DCE =60°,OC 平分∠AOB辅助线:过点C 作CM ⊥AO ,CN ⊥BO ,垂足分别为M 、N 结论:△CDM ≌△CEN ,CD =CE ,OD +OE =OC ,24OECD S =四边形45.对角互补模型-任意角全等型条件:∠AOB =2α,∠DCE =180°-2α,OC 平分∠AOB辅助线:过点C 作CM ⊥AO ,CN ⊥BO ,垂足分别为M 、N 结论:△CDM ≌△CEN ,CD =CE ,2cos OD OE OC α+=⋅, 2sin cos OEC OCD S S OC αα+=⋅46.邻边相等的对角互补模型条件:四边形ABCD 中,AB =AD ,∠ABC +∠ADC =180°D BAN E OB辅助线:延长CD 到E ,使得DE =BC ,连接AE结论:△ABC ≌△ADE ,CA 平分∠BCD十三、隐圆模型47.动点定长模型条件:AB =AC =AP ,点P 为动点结论:点B 、C 、P 三点共圆,点A 为圆心,AB 为半径48.直角圆周角模型条件:点C 为动点,∠ACB =90°结论:点A 、B 、C 三点共圆,线段AB 的中点为圆心,线段 AB 为直径49.定弦定长模型条件:点P 为动点,固定线段AB 所对的动角∠APB 为定值 结论:点A 、B 、P 三点共圆,线段AB 和BP 的中垂线的交点 为圆心BA50.四点共圆模型①条件:点A 、C 为动点,∠BAD +∠BCD =180°结论:点A 、B 、C 、D 四点共圆,线段AB 和BC 的中垂线的 交点为圆心当∠BAD =∠BCD =90°,BD 为直径51.四点共圆模型②条件:线段AB 为固定长度,点D 为动点,∠C =∠D结论:点A 、B 、C 、D 四点共圆,线段AB 和BC 的中垂线的 交点为圆心CCA当∠C=∠D=90°,AB为直径。

初中数学八大几何模型归纳
初中数学中的八大几何模型包括:
1. 三角形相关模型:三角形的各种性质、三角形的面积计算、三角形的周长计算等;
2. 四边形相关模型:四边形的各种性质、四边形的面积计算、四边形的周长计算等;
3. 圆相关模型:圆的各种性质、圆的面积计算、圆的周长计算、圆的弧长计算等;
4. 相似三角形相关模型:相似三角形的定义、相似三角形的判定、相似三角形的面积计算等;
5. 直角三角形相关模型:直角三角形的定义、直角三角形的判定、直角三角形的面积计算等;
6. 二次函数相关模型:二次函数的定义、二次函数的图像、二次函数的值域、二次函数的对称轴等;
7. 轴对称相关模型:轴对称的定义、轴对称的图像、轴对称的性质、轴对称的图形设计等;
8. 平移相关模型:平移的定义、平移的性质、平移的图像等。
这些几何模型是初中数学中非常重要的知识点,学生在学习过程中需要熟练掌握。
此外,这些模型也是中考数学考试中经常出现的知识点,学生需要在平时的学习中多加练习,熟练掌握各种计算方法和技巧。


有哪些初中数学模型
数学解题模型是解决几何问题的最佳途径。
套路很重要,但要想学好题套路,必须建立在理解的基础上。
因为题型会变,尤其是中考的命题趋势,不是一味追求难度,而是考察学生的灵活度。
所以首先要了解解题模式的本质,知其然,知其所以然。
党可以不变,应该变!
1,倍长中线模型
2,截长补短模型
3,一线三垂直模型
4,将军饮马模型
常见的还有手拉手模型、半角模型、奔驰模型、十字架模型、胡不归模型等等
想学好几何模型,不仅要知道为什么,还要知道为什么。
只有明确了原理,很多模型才能举一反三,一些新问题才能指明解决问题的方向。
比如一般的马饮模型的原理就是轴对称和三角形的两边之和大于第三边。
掌握原理后,你就可以轻松掌握一般马饮水的几个变形问题了。
此外,胡不归模型也是一般饮马的变形。
把握两种模式的区别和联系,可以快速学习胡不归模式。
郭老师,初中数学老师,从教15年。
开放式公益教学课程:郭数学公益课系列。
教初中数学各年级各章节考点和解题方法。
欢迎关注郭数学,免费学习。

初中数学几大模型及例题初中数学中的几大模型包括:将军饮马模型、胡不归模型、费马点模型、共线点模型和角平分线模型。
以下是对这些模型的简单介绍和相关例题:1. 将军饮马模型:此模型涉及直线上的两个点A和B,以及另一点C。
在此情况下,AC和CB的长度和最短的问题可以视为将军到饮马的地点所需要走的距离。
2. 例题:在锐角三角形ABC中,AD⊥BC于D,且BD=2,CD=3,那么AD的最小值是多少?3. 胡不归模型:此模型涉及到一个点A和两条射线l1和l2。
在A点到l1和l2的距离不同的情况下,求A点到l1和l2的最短距离。
4. 例题:已知点A(3,4),直线l1:x=1,直线l2:y=4。
求A点到l1和l2的最短距离。
5. 费马点模型:此模型涉及三个点A、B和C,以及三角形ABC的费马点P。
费马点是三角形内到三边的距离之和最小的点。
6. 例题:在锐角三角形ABC中,P是AB上的一个动点,求AP+BP+CP的最小值。
7. 共线点模型:此模型涉及到一个点和两条直线。
在此情况下,需要确定该点是否在给定的两条直线上。
8. 例题:已知点A(1,2)和直线l1:x+2y=0,判断A是否在l1上。
9. 角平分线模型:此模型涉及到一个角的平分线。
在此情况下,需要确定角平分线的性质及其应用。
例题:+ 已知等腰三角形ABC的角平分线AD交BC于D,且AD=3,BD=4,CD=5,求三角形的面积。
以上是初中数学中的几大模型及相关的例题。
这些模型是数学问题解决的关键工具,掌握它们有助于更好地理解和应用数学知识。

初中数学常用模型
1.百分数模型:将某个数值表示为百分数形式,例如将0.75表示为75%。
常用于比率和利率问题中。
2. 比例模型:将两个数值的比例表示为等式形式,例如a:b=c:d。
常用于物品的比较和分配问题中。
3. 均值模型:计算一组数值的平均值,例如(3+5+7)/3=5。
常用于统计和调查问题中。
4. 比率模型:将两个数值相除得到比率,例如a/b=2/3。
常用于比较和变化问题中。
5. 等比数列模型:一组数值成等比数列,例如1,2,4,8,16。
常用于变化和增长问题中。
6. 线性方程模型:将两个变量之间的关系表示为线性方程,例如y=mx+b。
常用于函数和图像问题中。
7. 面积和体积模型:计算几何图形的面积和立体图形的体积,例如矩形的面积为长×宽。
常用于几何和空间问题中。
8. 概率模型:计算某个事件发生的可能性,例如掷骰子得到1的概率为1/6。
常用于随机事件和实验问题中。
- 1 -。
初三数学几何模型大全
1. 平面图形,包括三角形(等边三角形、等腰三角形、直角三
角形等)、四边形(矩形、正方形、菱形、梯形等)、多边形(五
边形、六边形等)等。
2. 立体图形,包括立方体、正方体、棱柱(三棱柱、四棱柱)、棱锥(三棱锥、四棱锥)、圆柱、圆锥等。
3. 几何变换,包括平移、旋转、镜像、相似等几何变换的模型。
4. 圆的相关模型,包括圆的性质、圆的面积、圆的周长等相关
模型。
5. 空间几何,包括点、直线、平面、空间中的位置关系、投影
等相关模型。
在初三数学几何模型大全中,以上列举的只是一部分常见的内容。
学生在学习几何模型时,除了掌握这些基本的几何形状和概念外,还需要理解它们的性质、计算方法以及在实际问题中的应用等。
希望以上内容能够帮助到你,如果你有其他问题,欢迎继续提问。
初中数学的几何模型是学生学习数学时的重要内容之一,通过学习几何模型和解题,可以帮助学生对几何知识有更深层次的理解,提高数学解题能力。
本文将介绍初中数学中常见的48个几何模型及其相关题型,希望可以帮助学生系统地掌握几何知识。
一、直线和角1. 直线概念直线是由一点不停地延伸而成的。
在平面几何中,直线没有宽度和厚度,只有长度。
2. 角的概念两条相交直线之间的夹角叫做角。
角可以分为锐角、直角、钝角和平角。
3. 直线和角相关题型- 计算夹角的大小- 判断角的种类二、多边形1. 三角形三角形是最简单的多边形,其内角和为180度。
根据边的长度和角的大小,可以分为等腰三角形、等边三角形、直角三角形等不同种类。
2. 四边形四边形是具有四条边的几何图形,常见的四边形有矩形、正方形、平行四边形和菱形等。
3. 多边形相关题型- 计算多边形的内角和- 判断多边形的种类三、圆1. 圆的概念圆是由一个点到另一个点距离恒定的点的集合。
其中,点到圆心的距离为半径,圆上任意两点之间的距离称为弦。
2. 圆的性质圆的直径是圆的两个相对的端点,圆的周长和面积分别为2πr和πr²。
3. 圆相关题型- 计算圆的周长和面积- 判断圆的种类四、平面图形的平移、旋转和对称1. 平移平移是指将一个物体按照一定的规则移动到另一位置,移动前后的图形位置关系不变。
学生需要了解不同平移的规律和图形的位置关系。
2. 旋转旋转是指以某一点为中心,按一定角度将图形进行旋转。
学生需要掌握图形旋转的规律和性质。
3. 对称对称是指一个图形绕某条直线或点对称,对称轴可以分为水平对称轴、垂直对称轴和斜对称轴。
五、三视图和展开图1. 三视图三视图是指物体分别从正视图、侧视图和俯视图所得的图形。
学生需要根据给定的三视图还原出物体的整体图形。
2. 展开图展开图是将立体图形按一定规则展开成平面图形。
学生需要了解展开图的规律和方法。
六、空间图形1. 空间图形的概念空间图形是三维几何中的图形,包括圆柱、圆锥、球体、棱体等。
中考数学常见的11种几何模型一、三角形的不等关系模型:A字型、K字型、X字型1. 三角形两边之和大于第三边;2. 三角形两边之差小于第三边;3. 直角三角形斜边上的中线等于斜边的一半;4. 直角三角形中30度所对的直角边等于斜边的一半;5. 三角形三个内角之和等于180度。
二、全等、相似模型模型:A字型全等、A字型相似、8字型全等、8字型相似、蝴蝶型全等、蝴蝶型相似、平行型全等、平行型相似、等积模型等。
三、平行四边形模型模型:平行四边形ABCD中,E为AB中点,则:AC、DE互相平分;模型:平行四边形ABCD中,AC、BD交于O,则:AO=CO,BO=DO;模型:平行四边形ABCD中,AC平分角BAD,则:四边形ABCD为菱形。
四、梯形模型模型:梯形ABCD中,E为AD中点,则:延长BE交DC延长线于F,则:BE=FE;模型:梯形ABCD中,A、B在直线EF上,则:延长DC交AB延长线于F,则:梯形ABCD面积等于三角形面积的2倍;模型:梯形ABCD中,E为AD中点,则:延长BE交DC延长线于F,则:EF=FC。
五、矩形模型模型:矩形ABCD中,E为BC中点,则:AE平分角BAD;模型:矩形ABCD中,E为AD中点,则:AF平分角ABC;模型:矩形ABCD中,AC平分角BAD,则:四边形ABCD为菱形。
六、多边形模型模型:任意多边形ABCD中,E为AD中点,则:延长BE交DC延长线于F,则:BF=FE;模型:任意多边形ABCD中,E为AD中点,延长BE交DC延长线于F,则:EF=FC。
七、燕尾模型模型:在三角形ABC中,BD平分角ABC,CE平分角ACB,则:点D、E在BC同旁,则:三角形ADE的面积等于三角形ABC面积的一半。
八、风筝模型模型:在三角形ABC中,点D、E在BC上,且AD平分角BAE,则:三角形ABC与三角形ADE的面积相等。
九、铅笔模型模型:在矩形ABCD中,点E、F分别在AB、CD上,则:EF平行于AD,则:矩形ABFE与矩形EFCD相似。
2024年中考数学总复习初中数学常考10个几何模
型汇总
模型一:“12345”模型
模型二:“半角”模型
对称半角模型
旋转半角模型
模型三:“角平分线”模型
角平分线定理角平分线+垂线=等腰三角形角分线+平行线=等腰三角必呈现
角平分线+垂线=等腰三角形
模型四:“手拉手”模型
条件:1、两个等腰三角形;2、顶角相等;3、顶点重合。
结论:1、手相等;2、三角形全等;3、手的夹角相等;
4、顶点连手的交点得平分。
模型五:“将军饮马”模型
模型六:“中点”模型
【模型1】倍长
1、倍长中线;
2、倍长类中线;
3、中点遇平行延长相交
【模型2】遇多个中点,构造中位线
1.直接连接中点;
2.连对角线取中点再相连
模型七:“邻边相等的对角互补”模型
【模型1】
【条件】如图,四边形ABCD中,AB=AD,∠BAD+∠BCD=∠ABC+∠ADC=180°
【结论】AC平分∠BCD
【模型2】
【条件】如图,四边形ABCD中,AB=AD,∠BAD=∠BCD=90°【结论】①∠ACB=∠ACD=45°②BC+CD=V2AC
模型八:“一线三角”模型
【条件】∠EDF=∠B=∠C,且DE=DF
【结论】△BDE=△CFD
模型九:“弦图”模型
【条件】正方形内或外互相垂直的四条线段【结论】新构成了同心的正方形
模型十:费马点。
初中数学所有模型总结
初中数学是学生们学习最基础的数学知识和技能的阶段,其中模型是数学的重要组成部分。
数学模型是将现实问题转化为数学问题的过程,通过建立模型来解决实际问题。
在初中数学中,学生学习了多种不同类型的数学模型,如下所述:
1. 比例模型:比例模型是最常见的数学模型之一。
比例模型可以用来解决实际生活中的各种问题,如物品的价格、长度、时间等等。
学生需要对比例模型的基本概念和计算方法有深入的了解。
2. 几何模型:几何模型是在几何图形中建立的数学模型,如三角形、正方形、圆形等等。
几何模型可以用来解决实际问题,如计算面积、周长、角度等等。
3. 代数模型:代数模型是将实际问题抽象到代数符号中,建立代数方程来解决问题。
在初中数学中,学生需要学习代数符号的基础知识和代数方程的解法。
4. 统计模型:统计模型是用来分析和解释数据的数学模型。
在初中数学中,学生需要学习统计学基础知识和统计模型的使用方法。
5. 概率模型:概率模型是用来预测结果的数学模型。
在初中数学
中,学生需要学习概率基础知识和概率模型的使用方法。
总之,初中数学的模型种类繁多,每种模型都有其独特的应用和使用方法。
了解和掌握这些模型对于学生未来的学习和职业生涯都是非常重要的。
初中数学几何模型总结归纳1.中点模型【模型1】倍长1、倍长中线;2、倍长类中线;3、中点遇平行线延长相交ABCD E ABC DEFEDCBA【模型2】遇多个中点,构造中位线1、直接连接中点;2、连对角线取中点再相连GABCDEFABCD E【例1】在菱形ABCD 和正三角形BEF 中,∠ABC =60°,G 是DF 的中点,连接GC 、GE . (1)如图1,当点E 在BC 边上时,若AB =10,BF =4,求GE 的长;(2)如图2,当点F 在AB 的延长线上时,线段GE 、GC 有怎样的数量和位置关系,写出你的猜想,并给予证明;(3)如图3,当点F 在CB 的延长线上时,(2)问中的关系还成立吗?写出你的猜想,并给予证明.图3图2图1ACDEFGDEFGCDEGABBFCBA【解答】(1)延长EG 交CD 于点H 易证明△CHG ≌△CEG ,则GE =HBEGCFAD(2)延长CG 交AB 于点I ,易证明△BCE ≌△FIE ,则△CEI 是等边三角形,GE =3GC 错误!未找到引用源。
,且GE ⊥GCF(3)EJ【例2】如图,在菱形ABCD 中,点E 、F 分别是BC 、CD 上一点,连接DE 、EF ,且AE =AF ,∠DAE =∠BAF .(1)求证:CE =CF ; (2)若∠ABC =120°,点G 是线段AF 的中点,连接DG 、EG ,求证:DG ⊥EG .GFE DC BAE H GF EDCBA【解答】(1)证明△ABE ≌△ADF 即可;(2)延长DG 与AB 相交于点H ,连接HE ,证明△HBE ≌△EFD 即可【例3】如图,在凹四边形ABCD 中,AB =CD ,E 、F 分别为BC 、AD 的中点,BA 交EF 延长线于G 点,CD 交EF 于H 点,求证:∠BGE =∠CHE . 【解答】取BD 中点可证,如图所示:JA BCDE F GH2.角平分线模型【模型1】构造轴对称【模型2】角平分线遇平行构等腰三角形【例4】如图,平行四边形ABCD 中,AE 平分∠BAD 交BC 边于E ,EF ⊥AE 交边CD 于F 点,交AD 边于H ,延长BA 到G 点,使AG =CF ,连接GF .若BC =7,DF =3,EH =3AE ,则GF 的长为_______.HGFEDCBA【解答】延长FE 、AB 交于点I ,易得CE =CF ,BA =BE ,设CE =x ,则BA =CD =3+x ,BE =7-x , 3+x =7-x ,x =2,AB =BE =5,AE =,作AJ ⊥BC ,连接AC ,求得GF =AC =3JIAB CDEFGH3.手拉手模型【条件】OA =OB ,OC =OD ,∠AOB =∠COD【结论】△OAC ≌△OBD ,∠AEB =∠AOB =∠COD (即都是旋转角);OE 平分∠AEDDC EBAOOABEC D 导角核心图形:八字形CBAO【例5】(2014重庆市A 卷)如图,正方形ABCD 的边长为6,点O 是对角线AC 、BD 的交点,点E 在CD 上,且2DE CE ,连接BE .过点C 作CF ⊥BE ,垂足是F ,连接OF ,则OF 的长为________.FABCOEDDE CBA【例6】如图,△ABC 中,∠BAC =90°,AB =AC ,AD ⊥BC 于点D ,点E 在AC 边上,连接BE ,AG ⊥BE于F ,交BC 于点G ,求∠DFG . GFE DCBAABC【答案】45°【例7】(2014重庆B 卷)如图,在边长为ABCD 中,E 是AB 边上一点,G 是AD 延长线一点,BE =DG ,连接EG ,CF ⊥EG 交EG 于点H ,交AD 于点F ,连接CE 、BH .若BH =8,则FG=_____________.HGDE CBAFABE G【答案】4.邻边相等对角互补模型【模型1】【条件】如图,四边形ABCD 中,AB =AD ,∠BAD +∠BCD =∠ABC +∠ADC =180° 【结论】AC 平分∠BCDEB【模型2】【条件】如图,四边形ABCD 中,AB =AD ,∠BAD =∠BCD =90° 【结论】① ∠ACB =∠ACD =45°; ② BC +CDABCECB【例8】如图,矩形ABCD 中,AB =6,AD =5,G 为CD 中点,DE =DG ,FG ⊥BE 于F ,则DF 为_____.F ABCEDGG DE【例9】如图,正方形ABCD 的边长为3,延长CB 至点M ,使BM =1,连接AM ,过点B 作BN ⊥AM ,垂足为N ,O 是对角线AC 、BD 的交点,连结ON ,则ON 的长为__________. OMN DCBA【例10】如图,正方形ABCD 的面积为64,△BCE 是等边三角形,F 是CE 的中点,AE 、BF 交于点G ,则DG 的长为___________. GFEABCDEC【答案】45.半角模型【模型1】【条件】如图,四边形ABCD 中,AB =AD ,∠BAD +∠BCD =∠ABC +∠ADC =180°,∠EAF =12∠BAD , 点E 在直线BC 上,点F 在直线CD 上 【结论】BE 、DF 、EF 满足截长补短关系FEDCBA【模型2】【条件】如图,在正方形ABCD 中,已知E 、F 分别是边BC 、CD 上的点,且满足∠EAF =45°,AE 、AF 分别与对角线BD 交于点M 、N . 【结论】①BE +DF =EF ; ② ABE ADF AEF S S S ∆∆∆+=;③AH =AB ;④2ECF C AB ∆=;⑤BM 2+DN 2=MN 2;⑥△ANM ∽△DNF ∽△BEM ∽△AEF ∽△BNA ∽△DAM (由AO :AH =AO :AB =1:可得到△ANM 和△AEF 相似比为1)⑦AMN MNFE S S ∆=四边形;⑧△AOM ∽△ADF ;△AON ∽△ABE ;⑨△AEN 为等腰直角三角形,∠AEN =45°,△AFM 为等腰直角三角形,∠AFM =45°;⑩A 、M 、F 、D 四点共圆,A 、B 、E 、N 四点共圆,M 、N 、F 、C 、E 五点共圆.H NM FEDCBA【模型2变形】【条件】在正方形ABCD 中,已知E 、F 分别是CB 、DC 延长线上的点,且满足∠EAF =45° 【结论】BE +EF =DFFEDCB A【模型2变形】【条件】在正方形ABCD 中,已知E 、F 分别是BC 、CD 延长线上的点,且满足∠EAF =45° 【结论】DF +EF =BEAB C DEF【例11】如图,△ABC 和△DEF 是两个全等的等腰直角三角形,∠BAC =∠EDF =90°,△DEF 的顶点E与△ABC 的斜边BC 的中点重合,将△DEF 绕点E 旋转,旋转过程中,线段DE 与线段AB 相交于点P ,射线EF 与线段AB 相交于点G ,与射线CA 相交于点Q .若AQ =12,BP =3,则PG =__________.Q PGD FECBA【解答】连接AE ,题目中有一线三等角模型和半角模型设AC =x ,由△BPC ∽△CEQ 得BP CE =BE CQ , 3/(22x )=22x /(x +12),解得x =12 设PG =y ,由AG 2+BP 2=PG 2得32+(12-3-x )2=x 2,解得x =5【例12】如图,在菱形ABCD 中,AB =BD ,点E 、F 在AB 、AD 上,且AE =DF .连接BF 与DE 交于点G ,连接CG 与BD 交于点H ,若CG =1,则S 四边形BCDQ =__________.HGFED CB A【解答】346.一线三等角模型【条件】∠EDF =∠B =∠C ,且DE =DF 【结论】△BDE ≌△CFDFEDCBA【例13】如图,正方形ABCD 中,点E 、F 、G 分别为AB 、BC 、CD 边上的点,EB =3,GC =4,连接EF 、FG 、GE 恰好构成一个等边三角形,则正方形的边为__________.GA B CDEF【解答】如图,构造一线三等角模型,△EFH ≌△FGI 则BC =BF +CF =HF -BH +FI -CI =GI -BH +HE -CI =733IH F ED C B A G7.弦图模型【条件】正方形内或外互相垂直的四条线段 【结论】新构成了同心的正方形LK JIHGFECDB AHG FEDCBA【例14】如图,点E 为正方形ABCD 边AB 上一点,点F 在DE 的延长线上,AF =AB ,AC 与FD 交于点G ,∠F AB 的平分线交FG 于点H ,过点D 作HA 的垂线交HA 的延长线于点I .若AH =3AI ,FH =22,则DG =__________.I H AGFEDCB【解答】1742【例15】如图,△ABC 中,∠BAC =90°,AB =AC ,AD ⊥BC 于点D ,点E 是AC 中点,连接BE ,作AG ⊥BE 于F ,交BC 于点G ,连接EG ,求证:AG +EG =BE .FE CGDBABC【解答】过点C 作CH ⊥AC 交AG 的延长线于点H ,易证8.最短路径模型【两点之间线段最短】 1、将军饮马Q2、费马点【垂线段最短】【两边之差小于第三边】【例16】如图,矩形ABCD 是一个长为1000米,宽为600米的货场,A 、D 是入口,现拟在货场内建一个收费站P ,在铁路线BC 段上建一个发货站台H ,设铺设公路AP 、DP 以及PH 之长度和为l ,求l 的最小值.【解答】3500600 ,点线为最短.【例17】如图,E 、F 是正方形ABCD 的边AD 上的两个动点,满足AE =DF,连接CF 交BD 于G ,连接BE 交AG 于H ,若正方形的边长为2,则线段DH 长度的最小值为______________________.【解答】如图,取AB 中点P ,连接PH 、PD ,易证PH ≥PD -PH 即DH ≥15-.【例18】如图所示,在矩形ABCD 中,AB =4,AD =24,E 是线段AB 的中点,F 是线段BC 上的动点,△BEF 沿直线EF 翻折到△EF B ',连接B D ',B D '最短为________________.【解答】4【例19】如图1,□ABCD 中,AE ⊥BC 于E ,AE =AD ,EG ⊥AB 于G ,延长GE 、DC 交于点F ,连接AF .(1)若BE =2EC ,AB =13,求AD 的长;(2)求证:EG =BG +FC ;(3)如图2,若AF =25,EF =2,点M 是线段AG 上一动点,连接ME ,将△GME 沿ME 翻折到△ME G ',连接G D ',试求当G D '取得最小值时GM 的长.图1 图2 备用图【解答】(1)3(2)如图所示(3)当DG ′最小时D 、E 、G '三点共线解得43173-=+'=MN N G GMEH【练习1】如图,以正方形的边AB为斜边在正方形内作直角三角形ABE,∠AEB=90°,AC、BD交于O.已知AE、BE的长分别为3、5,求三角形OBE的面积.【解答】25【练习2】问题1:如图1,在等腰梯形ABCD 中,AD∥BC,AB=BC=CD,点M,N分别在AD,CD上,∠MBN21∠ABC,试探究线段MN,AM,CN有怎样的数量关系?请直接写出你的猜想;问题2:如图2,在四边形ABCD中,AB=BC,∠ABC+∠ADC=180°,点M,N分别在DA,CD延长线,若∠MBN=12∠ABC仍然成立,请你进一步探究线段MN,AM,CN又有怎么样的关量关系?写出你的猜想,并给予证明。
初 中 数 学 几 个 数 学 模 型①圆锥母线长5cm ,底面半径长3cm ,那么它的侧面展开图的圆心角是 216 。
②劳技课上,王芳制作了一个圆锥形纸帽,其尺寸如图.则将这个纸帽展开成扇形时的圆心角等于( C ) A .45° B.60° C .90° D.120°③要制作一个圆锥形的模型,要求底面半径为2cm ,母线长为4cm ,在一个边长为8cm 的正方形纸板上,能否裁剪制作一个这种模型(侧面和底面要完整,不能拼凑)( C ) (A)一个也不能做 (B)能做一个 (C)可做二个 (D)可做二个以上 4、(2004河北T7)在正方形铁皮上剪下个圆形和扇形,使之恰好围成如图所示的圆锥模型.设圆的半径为r,扇形的半径为R,则圆半径与扇形半径之间的关系是 (D )A 、2r=R B 、R r =49 C 、R r =3 D 、r 4模型2如图,∆ABC 中BD 、CD 平分∠ABC 、∠ACB ,过D 作直线平行于BC ,交AB 、AC 于E 、F ,当∠A 的位置及大小变化时,线段EF 和BE+CF 的大小关系( B ).(A )EF>BE+CF (B )EF=BE+CF (C )EF<BE+CF (D )不能确定模型3①在△ABC 中,a=1,b=3,∠A=300,则∠B=___60___度。
②两个全等的含300, 600角的三角板ADE 和三角板ABC 如图所示放置,E,A,C 三点在一条直线上,连结BD ,取BD 的中点M ,连结ME ,MC .试判断△EMC 的形状,并说明理由.(等腰直角三角形)③(2006邵阳T8. ) 将一副三角板按图(一)叠放,则△AOB 与△DOC 的面积之比等于(1:3 )④(2005年浙江绍兴T18.)(以下两小题选做一题,第(1)小题满分5分,第(2)小题满分为3分。
若两小题都做,以第(1)小题计分) 选做第________小题,答案为________(1) 将一副三角板如图叠放,则左右阴影部分面积1S :2S 之比等于________ (2) 将一副三角板如图放置,则上下两块三角板面积1A :2A 之比等于________⑤(2006年武汉市T24.10分)已知:将一副三角板(Rt △ABC 和Rt △DEF )如图①摆放,点E 、A 、D 、B 在一条直线上,且D 是AB 的中点。
将Rt △DEF 绕点D 顺时针方向旋转角α(0°<α<90°),在旋转过程中,直线DE 、AC 相交于点M ,直线DF 、BC 相交于点N ,分别过点M 、N 作直线AB 的垂线,垂足为G 、H 。
(1)当α=30°时(如图②),求证:AG =DH ;(2)当α=60°时(如图③),(1)中的结论是否成立?请写出你的结论,并说明理由;(3)当0°<α<90°时,(1)中的结论是否成立?请写出你的结论,并根据图④说明理由。
⑥一副三角板由一个等腰直角三角形和一个含300的直角三角形组成,利用这副三角板构成一个含有150角的方法较多,请你画出其中两种不同构成的示意图,并在图上标出必要的标注,不写作法.⑦将一副三角尺如图摆放一起,连接AD, 则∠ADB 的余切值为 .⑧如图,ABC ∆中,︒=∠90ACB ,︒=∠30B ,1=AC ,过点C 作AB CD ⊥1于1D ,A G D H M E F C BN第24题图图③ EF M N D A BGH 图④ C 45° 60°A E DBC F A GD H ME FC B (N )第24题图 图① 图②过1D 作BC D D ⊥21于2D ,过2D 作AB D D ⊥32于3D ,这样继续作下去,……,线段1+n n D D 能等于(n 为正整数)(A) n⎪⎭⎫ ⎝⎛23 (B) 123+⎪⎭⎫⎝⎛n (C)n ⎪⎪⎭⎫ ⎝⎛23 (D)123+⎪⎪⎭⎫⎝⎛n⑨已知∠AOB=90°,OM 是∠AOB 的平分线,按以下要求解答问题: (1)将三角板的直角顶点P 在射线OM 上移动,两直角边分别与边OA ,OB 交于点C ,D.. ①在图甲中,证明:PC=PD ;②在图乙中,点G 是CD 与OP 的交点,且PG=23PD ,求△POD 与△PDG 的面积之比.(2)将三角板的直角顶点P 在射线OM 上移动,一直角边与边OB 交于点D ,OD=1,另一直角边与直线OA ,直线OB 分别交于点C ,E ,使以P ,D ,E 为顶点的三角形与△OCD 相似,在图丙中作出图形,试求OP 的长.⑩如图,客轮沿折线A -B -C 从A 出发经B 再到C 匀速航行,货轮从AC 的中点D 出发沿某一方向匀速直线航行,将一批物品送达客轮。
两船同时起航,并同时到达折线A -B -C 的某点E 处,已知AB =BC =200海里,∠ABC =90°,客轮速度是货轮速度的2倍。
(1)选择:两船相遇之处E 点( )。
A 、在线段AB 上 B 、在线段BC 上 C 、可以在线段AB 上,也可以在线段BC 上 (2)求货轮从出发到两船相遇共航行了多少海里?(结果保留根号)。
⒒将一把三角尺放在边长为1的正方形ABCD 上,并使它的直角顶点P 在对角线AC 上滑动,AB O M 图丙 A B CO PM D 图乙 图甲 D M P O CB A (第⑧题图)CA C B1D 2D4D6D5D 3D直角的另一边始终经过点B ,另一边与射线DC 相交于点Q 。
设A 、P 两点间的距离为x , (1)当点Q 在CD 上时,线段PQ 、PB 之间有怎样的大小关系?试证明你观察到的结论。
(2)当点Q 在CD 上时,求四边形PBCQ 的面积y 与x 的函数解析式,并求出X 的取值范围; (3)当点P 在线段AC 上滑动时,三角形PCQ 是否能为等腰三角形?如果可能,指出所有可能使三角形PCQ 成为等腰三角形的点Q 的位置,并求出相应的X 的值;如果不能说明理由(以下三个图的形状,大小相同,以供操与解题时备用) 解:(1)PQ=PB证明:连接BD 交AC 于点O ,连接PD ,如图(1) 四边形ABCD 是正方形∴ AC 垂直平分BD ,045=∠=∠OCD ODC ∴ PB=PD ,0904=∠+∠∴ 21∠=∠ 图 (1)PQPB PQ PD PQD PDQ OCD PQD ODC PDQ PD PB =∴=∴∠=∠∴+∠=∠+∠=∠+∠=∠+∠=∠∠=∠∴∠=∠∴=∠+∠∴⊥0004533452232319043 ……………………………..4分(2)连接BD 交AC 于点O ,作QE AC ⊥于点E (如图2))21(121)2)(2(21)(212290,,20<≤+-=∴-+=+=+=∴-=-==∴∆≅∆∴=∠=∠∠=∠=∆∆x x y x x QE BO PC S S S xAP OA OP QE QEPPOB QEP POB QPE PBO PQ PB PCQ PBC PBCQ ………………………………………………4分 (3)可能当P 与A 重合时,Q 与D 重合,有PQ=QC ,X=0 当PC=CQ 时,且Q 在DC 的延长线上时,(图形3),连接BD 交AC 于点O ,连接BQ ,则CQ=PC=2222)2(1,2x CQ BC BQ x -+=+=-由(1)证得,PB=PQ ,ABCQC Q[]222)2(121)22(x BQ PB -+==∴由[]1)22()22()2(121222222=∴-+=-=∴+=x x x OP BO PB …………….3分12.如图,操作:将一把三角尺放在边长为1的正方形ABCD 上,并使它的直角顶点P 在对角线AC 上滑动,直角的一边始终经过点B ,另一边与边DC 或射线DC 相交于点Q 。
当点Q 在边CD 上时,线段PQ 与线段PB 之间有怎样的大小关系?试证明你观察得到的结论;② 当点Q 在边CD 运动上时,设四边形PBCQ 的面积为S 时,试用含有x 的代数式表示S :③ 当点P 在线段AC 上滑动时,△PCQ 是否可能成为等腰三角形?如果可能,指出所有能使△PCQ 成为等腰三角形的点Q 的位置,并求出相应的x 的值;如果不可能,试说明理由。
①过点P 作PE AB ⊥ 交AB 于E, 过点P 作PF CD ⊥交BC 于F -----1分 PE=AE,BE=1-AE,PF=1-PE=1-AE ∴BE=PF ------2分090EPB FPQ ∠+∠=090EPB EBP ∠+∠=∴EBP FPQ ∠=∠------3分∴ PEB PFQ ∆≅∆ ------4分 ∴PB=PQ --------5分 设PM=x,BM=1-x, QC=1-x-x=1-2x21122111(21)22PBC PCQS S SBC PM CQ PF x x x x ∆=+=⨯⨯+⨯=⨯⨯+-=-----------8分③有可能成为等腰三角形,求出x 值-------11分 13.(12分)用两个全等的等边三角形△ABC 和△ACD 拼成菱形ABCD.把一个含60°角的三角尺与这个菱形叠合,使三角尺的60°角的顶点与点A 重合,两边分别与AB ,AC 重合.将三角尺绕点A 按逆时针方向旋转.(1)当三角尺的两边分别与菱形的两边BC ,CD 相交于点E ,F 时,(如图13—1),通过观察或测量BE ,CF 的长度,你能得出什么结论?并证明你的结论;(2)当三角尺的两边分别与菱形的两边BC ,CD 的延长线相交于点E ,F 时(如图13—2),BC DQ你在(1)中得到的结论还成立吗?简要说明理由.(1)BE=CF. ……2分证明:在△ABE 和△ACF 中, ∵∠BAE+∠EAC=∠CAF+∠EAC=60°, ∴∠BAE=∠CAF. ∵AB=AC ,∠B=∠ACF=60°,∴△ABE ≌△ACF (ASA ). ……4分∴BE=CF. ……6分(2)BE=CF 仍然成立. 根据三角形全等的判定公理,同样可以证明△ABE 和△ACF 全等,BE 和CF 是它们的对应边.所以BE=CF 仍然成立.………………………………10分 27.(8分)等腰△ABC ,AB=AC=8,∠BAC=120°,P 为BC 的中点,小慧拿着含 30°角的透明三角板,使30°角的顶点落在点P ,三角板绕P 点旋转.(1)如图1,当三角板的两边分别交AB 、AC 于点E 、F 时.问△BP E 与△CFP 是否相似; (2)操作:将三角板绕点P 旋转到图2情形时,三角板的两边分别交BA 的延长线、边AC 于点E 、F .① 探究1:△BP E 与△CFP 还相似吗?(只需写出结论)② 探究2:连结EF ,△BP E 与△PFE 是否相似?请说明理由; ③ 设EF=m ,△EPF 的面积为S ,试用m 的代数式表示S .(1)如图,由题意得∠FPC+∠BPE=150, ∠BEP+∠BPE=150∴∠BEP=∠FPC 又∵∠B=∠C=30∴△BP E ~△CFP ………………… 2分(2)①△BP E 与△CFP 还相似 …………………………………… 3分 ②△BP E 与△PFE 相似, …………………………………… 4分由△BP E 与△CFP 相似,得 FP PE CP BE = ,又∵BP=CP ∴FPPEBP BE = , 即FPBPPE BE =,又∵∠B=∠EPF=30 ∴△BP E ~△PFE …………… 6分(1)(2)③如图,∵△BP E ~△PFE ,∴∠PEB=∠PEF 作PH ⊥BE 于点H,PG ⊥EG 于点G,则PH=PG ……… 7分在Rt △BPH 中, PBH BP PH ∠⋅=sin =32 ∴S=m 3 ……………… 8分模型4在上图中隐含有以下重要性质:⑴两对相等的锐角;∠A= ∠BCD ,∠B= ∠ACD⑵三对相似三角形:⊿ACD ∽⊿ CBD ∽⊿ABC, AC 2=AD ·AB BC 2=BD ·AB CD 2=BD ·AD ⑶边之比的推广⑷面积:AC ·BC=AB ·CD ⑸勾股定理⑹AB 是ΔABC 外接圆的直径 ①②③④⑤ ∽模型5①②③④⑤⑧增长率与百分数问题 iii 某商品降价20%后出售,一段时间后恢复原价,则应在售价的基础上提高的百分数是 ( )A 、20% B 、25% C 、30% D 、35%某商品经过两次降价,由每件100元降至81元,则平均每次降价的百分率为( ) A 、8.5% B 、9% C 、9.5% D 、10% iii模型6①如图:一个残破的圆钢轮,为了再铸做一个同样大小的圆轮,请用圆规、直尺作出它的圆心(不用写作法,保留作图痕迹)。