下载文档原格式
第六章 经典质点系动力学6-1．如图，半圆柱立在光滑水平面上从静止开始到下，试判断质心C 的运动方向．解 建立如图x 轴，由于水平方向外力分量之和为零0ix F =∑，所以水平方向动量守恒x P C =．因初始时静止，故 0x Cx P mv == 由d 0d C Cx x v t ==，可知C x =常量，质心C 竖直向下运动． 6-2．如图，船的质量为5000kg ，当质量为1000kg 的汽车相对船静止时，船尾螺旋桨的转动可使船以加速度20.2m s 前进．在船行进中，汽车相对于船以加速度20.5m s 沿船前进的相反方向加速运动，求此时船的加速度的大小．解 将船与汽车作为质点系．当汽车相对于船静止时，船的加速度即为质点系质心的加速度，根据质心运动定理可知船尾螺旋桨转动时的推力()=(50001000)021200(N)e C F ma .=+⨯=在船的行进过程中，以船的行进方向为x 、x '轴正方向．设船相对于岸的速度、加速度用x 、x 表示，汽车相对于船的速度、加速度用x '、x '表示，则汽车相对于岸的速度、加速度为x x '+、x x '+．根据质点系的动量定理()d [()]d e m x m x x F t'++=船车 即 ()()]e m x m x x F '++=船车500010001000051200x x .+-⨯=可求出此时船的加速度的大小2028m s x .=．6-3．三只质量均为0m 的小船鱼贯而行，速率都是v ，中间一船同时以相对本船的速率u 沿水平方向把两个质量均为m 的物体抛到前后两只船上，求两物体落入船后三只船的速率（忽略水对船的阻力）．解 以船行方向为速度正方向，设两物体落入船后三只船的速率为1v 、2v 、3v ． 以中间船及两物体为质点系，因为在抛出物体的过程中水平方向不受外力，所以质点系水平方向动量守恒00222(2)()()m m v m v m v u m v u +=+++-所以 2v v =以前船与抛入物体为质点系，因为在抛入物体的过程中水平方向不受外力，所以质点系水平方向动量守恒001()()m v m v u m m v ++=+所以 10mu v v m m=++ 以后船与抛入物体为质点系，同样，根据质点系水平方向动量守恒003()()m v m v u m m v +-=+30mu v v m m =-+6-4．质量为70kg 的人和质量为210kg 的小船最初处于静止，后来人从船尾向船头走了3.2m ，不计船所受阻力，问船向那个方向运动，移动了几米？（用质心运动定理求解．）解 建立与地面固连的坐标系Ox ，x 轴的方向为从船尾指向船头．人视为质点1，坐标为1x ；船视为质点2，坐标为2x ；此二质点构成质点系．质点系所受合外力为零，由质心运动定理可知质点系质心加速度为零；由于质心速度为常量，质点系初始状态静止，所以质心速度为零，即质心位置保持不变 110220112201212C C m x m x m x m x x x m m m m ++===++ 11220m x m x ∆+∆=由于123.2x x ∆=+∆，代入上式得12123.2 3.2700.8(m)70210m x m m ⨯∆=-=-=-++ 即船向后移动了0.8米．6-5．试证明质量为m ，长为l 的匀质细杆对过杆中点且与杆垂直的轴的转动惯量为2112ml ． 证明 以杆中心为原点，沿杆建立坐标系Oxy 如图．杆的线密度l m lρ=（即单位长度的质量）． 用一系列与杆垂直的不同x 的面，把杆分割成无限多个无限小的质元，图中画出了在~d x x x +范围内的小质元．此小质元质量d d d l m m x x lρ==，到Oy 轴的距离为||x ，对Oy 轴的转动惯量为22d d d m I x m x x l==．则整个细杆对Oy 轴的转动惯量 /223/22/2/211d 312l l l l m m I x x x ml l l --===⎰6-6．如图，半径0.1m R =的定滑轮，可绕过轮心的z 轴转动，转动惯量为20.1kg m J =⋅．一不可伸长之轻绳无滑地跨过定滑轮，一端竖直地悬一质量1kg m =的重物，另一端a 受竖直向下的力F 作用，20.8N F =．试用质点系角动量定理求a 点加速度．解 用滑轮、绳、重物构成质点系，质点系所受外力为F 、重物重力mg 和轮轴处所受支撑力N F ．根据质点系对z 轴的角动量定理2d d ()()d d J Rmv J mR FR mgR t tωω+=+=- 所以2d d FR mgR t J mR ω-=+，a 点加速度为 22d d F mg a R i R i t J mR ω-==+ 220.819.80.01 1.0(m s )0.110.01i i -⨯==+⨯6-7．可利用阿特伍德机（例题6-3-4）测滑轮转动惯量．设10.46kg m =，20.50kg m =，滑轮半径0.05m R =．由静止开始释放重物测得2m 在5.0s 内下降0.75m ．求滑轮转动惯量J ．解 （因为不要求求出绳内张力，故可用质点系角动量定理求解．）用滑轮、绳、重物构成质点系，质点系所受外力为重物和滑轮的重力、以及轮轴处所受支撑力N F ．根据质点系对z 轴的角动量定理1122d ()d J Rm v Rm v t ω++ 21221d [()]d J m m R m gR m gR tω=++=- 所以21212()d d ()m m gR t J m m Rω-=++，2m 下降加速度的大小为 212212()d d m m g a R t m m J R ω-==++ 可见质点2m 作匀加速直线运动．由2212x a t ∆=，求出220.060m s a =．由上式可知 221122()[]m m g J R m m a -=-- 222(050046)98005[050046]13910kg m 006........--⨯=⨯--=⨯⋅6-8．匀质细杆长2l ，质量为0m ，杆上穿有两个质量均为m 的小球．初始时杆以角速度0ω绕过杆中点O 且与杆垂直的光滑竖直轴转动，两小球均位于距O 点2l 处．求当两个小球同时滑动到杆的两端点时杆的角速度的大小．解 将杆和两个小球作为质点系．由于竖直轴光滑，轴受到的约束力对竖直转动轴力矩为零；细杆和小球的重力与竖直转动轴平行，对竖直转动轴力矩为零．由于质点系所受外力对竖直转动轴合力矩为零，所以质点系对竖直转动轴角动量守恒，设末态角速度为ω，则002222l l J m J ml l ωωωω+⋅=+⋅ 由于220011(2)123J m l m l ==，所以000(23)2(6)m m m m ωω+=+．6-9．工程上常用摩擦啮合器使两个飞轮以相同的转速转动，如图，飞轮A 、B 可绕同一固定轴转动，C 为啮合器．设飞轮A 、B 对轴的转动惯量210kg m A J =⋅，220kg m B J =⋅，开始A 轮转速600r min A n =（转每分），B 轮静止，求两轮啮合后的转速．解 将二飞轮A 、B 作为质点系．由于二飞轮所受重力和支撑力对固定轴力矩均为零，飞轮所受外阻（动）力矩比二飞轮啮合时飞轮间的相互作用力矩小得多，故啮合过程中质点系对固定轴的角动量近似守恒，有2()2A A A B J n J J n ππ⋅=+10600200(r min )1020A A A B J n n J J ⨯===++6-10．有两根原长为0l 、劲度系数为k 的轻弹簧串接于O 点，另两端各系一质量为m 的滑块，置于光滑水平面上．现将两滑块拉开，使其相距2l （0l l >），从静止放手，求两弹簧恢复原长时，弹簧弹性力对两滑块做功之和．（用三种方法求解）解法一 由于在运动过程中O 点为质心，由质心运动定理可知O 点固定不动．利用弹簧弹性势能求解．弹簧弹性力对两滑块做功之和等于两弹簧弹性势能增量的负值220012[0()]()2W k l l k l l =-⨯--=- 解法二 由于在运动过程中O 点为质心，由质心运动定理可知O 点固定不动．在惯性系中积分求功．以弹簧自由伸长处为原点、沿弹簧建立x 轴，则00220012()d 2()()2l l W kx x k l l k l l -=⨯-=⨯-=-⎰ 解法三 由于在运动过程中O 点为质心，由质心运动定理可知O 点固定不动．利用求一对力做功之和的方法，在与一个滑块相对静止的参考系中积分求功．以一个滑块为原点、沿弹簧建立x 轴，当另一滑块位于x 处时，每个弹簧的伸长量为02x l - 00220022[()]d 2()d()222l l l l x x x W k l x k l =--=--⎰⎰ 022202012()|()22l l x k l k l l =--=-6-11．两个滑冰运动员质量均为70kg ，均以6.5m s 速率沿相反方向滑行，滑行路线间的垂直距离为10m ．当彼此相错时，各抓住10m 长绳的一端，然后开始旋转．（1）在抓住绳端之前，各自对绳中点的角动量多大？抓住后又为多大？（2）他们各自收绳，到绳长5m 时，各自速率多大？（3）绳长5m 时绳内张力多大？（4）收绳过程中二人总动能如何变化？（5）二人共做多少功？解 （1）抓绳之前，每个运动员对绳中心角动量均为570 6.5L =⨯⨯22275(kg m s)=⋅． 抓绳之后，视两个运动员和绳为质点系，所受外力矢量和为零，所以质点系质心（绳中心）位置不变，绳中心仍为固定点，每个运动员对绳中心的角动量仍为22275kg m s ⋅．（2）绳的张力T F 为质点系内力．收绳过程中质点系所受外力对绳中心的力矩为零，所以质点系的角动量守恒，设收绳后运动员速率为v ，则 2 2.57022275v ⨯⨯⨯=⨯ 所以13m s v =．（3）当绳长5m 时，对每一个运动员，由牛顿第二定律可得2T 70134732(N)2.5F ⨯== （4）质点系总动能的增量等于组成质点系的每个质点动能增量之和22k k01270(13 6.5)8873(J)2E E -=⨯⨯⨯-= （5）根据质点系的动能定理，二运动员总共做功等于质点系动能增量，k k08873(J)W E E =-=6-12．匀质细杆长7m 5l =，质量为m ，可绕过其一端的光滑水平轴在竖直平面内转动，在杆自由下垂时有一质量为6m 的黏性小球沿水平方向飞来并黏附于杆的中点，使杆摆动的最大角度为60ο．求小球飞来时的速率．（210m g =）解 在小球与杆的碰撞过程中，以小球和杆为质点系．质点系所受外力中，杆的重力mg 和杆所受轴的支撑力N F 对轴O 的力矩为零；小球重力m g '对轴O 的力矩近似为零；所以质点系的角动量近似守恒221[()]262362l m l m l m v v ml ω'==+ 故92v l ω=．在小球和杆一起上摆的过程中，以小球和杆为质点系，仅有小球和杆所受重力做功，而重力为保守力，所以机械能守恒22211[()]()cos60236262m l m l ml m g ωο+=+ 因此2149g lω=．根据以上结果即可求出9146321(m s)292g v l gl l ===．6-13．在光滑水平桌面上，有一质量为m 的滑块，滑块与一弹簧相连，弹簧另一端固定于O 点，劲度系数为k ．当弹簧处于原长0l 时，一质量为0m 的子弹以速度0v 垂直于弹簧地射入滑块，并嵌在其中．之后当滑块运动到B 点时，弹簧长度为l ，如图所示．求滑块于B 时的速度v ．解 在子弹射入滑块的过程中，由子弹和滑块构成质点系．因质点系在0v 方向不受外力，故质点系沿0v 方向动量守恒000()m v m m v '=+所以000()v m v m m '=+．在子弹和滑块由A B →的过程中，视子弹和滑块为一个质点．由于过程中只有弹簧弹性力做功，弹簧弹性力为保守力，故质点机械能守恒；又因质点受力对过O 点的竖直轴力矩为零，所以质点对过O 点的竖直轴角动量守恒．222000111()()()222m m v m m v k l l '+=++- 000()()sin m m v l m m vl θ'+=+所以 22212000200()[]()m v k l l v m m m m -=-++ 000222120000arcsin [()()]m v l l m v m m k l l θ=-+-6-14．大容器内水的自由表面的高度为0h ，放在水平地面上，离自由表面h 深处有一小孔A ，小孔横截面积远小于容器横截面积．求：（1）由小孔A 流出的水流到达地面的水平射程x ；（2）与小孔A 在同一竖直线上，距自由表面多深处再开一孔，可使水流的水平射程与前者相等？（3）在多深处开孔，可使水流具有最大水平射程？最大水平射程是多少？解 （1）由于容器横截面积远大于小孔横截面积，水流稳定后可认为容器中水面高度不变．认为水是理想流体．水流稳定后，取一条从容器中水自由表面到小孔的流线，以容器底为重力势能零点，由伯努利方程200001()2gh p g h h v p ρρρ+=-++所以小孔流速2v gh =．流体微团从流出小孔到落地降落的高度2012h h gt -=，可知降落时间02()h h t g-=，因此水平射程02()x vt h h h ==-． （2）在h '深处另开一孔而水平射程相同，则由002()2()h h h h h h ''-=-可求出0h h h '=-．（略去h h '=．）（3）根据（1）02()x h h h =-，由002(2)d 0d 2()h h x h h h h -==-，有唯一极值点012h h =使水流具有最大射程．当012h h =时，max 0x x h ==．6-15．如图是测量液体流量的流量计原理图．已知细管和粗管的横截面积为1S 、2S ，使用时把它串接在水平液流管道中，稳定流动时两竖直管内液体自由表面高度差为h ．求流量表达式．解 沿管道中心轴取一流线，对该流线上1、2两点，根据伯努利方程，因12h h =，故2211221122v p v p ρρ+=+ （1） 连续性方程 1122v S v S = （2） 1、2两点压强差 21p p gh ρ-= （3） 由（1）、（3）式，可得22122v v gh -=由（2）式，得1122v S v S =，代入上式 221122(1)2S v gh S -= ，即1222212gh v S S S =- 所以 11221222212gh Q v S v S S S S S ===-6-16．如图装置，出口处堵塞时，注满可视为理想流体的水．水平细管横截面积处处相等，其直径远小于大容器直径．打开塞子在水流稳定后，求两竖直细管内水面高度．解 由于细管直径远小于大容器直径，水流稳定后可认为大容器中水面高度不变．在水流稳定之前，竖直细管内的水会流出，而水流稳定后竖直细管内水面高度不变．作从大容器水面开始经水平细管的流线，取水平细管处为势能零点，根据伯努利方程22201223304111222p gh p v p v p v ρρρρ+=+=+=+ 因为234S S S ==，根据连续性方程223344S v S v S v ==可得 234v v v ==所以 230p p p ==两竖直细管内为静止流体，根据2002p p p gh ρ==+3003p p p gh ρ==+所以230h h ==．6-17．如题6-16图，若其中装有密度为31000kg m 的黏性流体，流动稳定后10.18m h =，20.1m h =，30.05m h =．求出口流速．（不计大容器内内能量损失）解 由于细管直径远小于大容器直径，水流稳定后可认为大容器中水面高度不变．在水流稳定之前，竖直细管内的水会流出，而水流稳定后竖直细管内水面高度不变．作从大容器水面开始经水平细管的流线，取水平细管处为势能零点．根据连续性方程，因为水平细管横截面处处相等，故水平细管中的2、3、4点流速相等，以v 表示其流速．根据不可压缩黏性流体作稳定流动时的功能关系式，对3、4点，有2230341122p v p v W ρρ+=++ 竖直细管内为静止流体，可知303p p gh ρ=+，所以 343W gh ρ=根据不可压缩黏性流体作稳定流动时的功能关系式，对1、4点，有20101412p gh p v W ρρ+=++ 由于水平细管横截面处处相等，不计大容器内内能量损失，故可知34143W W =，所以132(3)298(0183005)0767(m s)v g h h ....=-=⨯⨯-⨯=（第六章题解结束）。
【北航考研辅导班】北航航空科学与工程学院考研科目参考书考研大纲考研分数线报录比考研经验一、北航航空科学与工程学院简介-启道航空科学与工程学院是北航最具有航空航天特色的院系之一,前身是飞机系，成立于1952年，首任系主任是“两弹一星”功勋科学家屠守锷院士。
主要从事大气层内各类航空器（飞机、直升机、飞艇等）、临近空间飞行器、微小型飞行器等的总体设计、气动、结构、强度、飞行力学、人机环境控制等方面的基础性、前瞻性、工程型以及新概念、新理论、新方法研究与教育工作。
曾成功研制了“北京一号”中程旅客机、“蜜蜂”系列轻型飞机、共轴双旋翼飞机，填补了国内空白。
半个多世纪以来培养了大批杰出人才，包括原全国人大副委员长李沛瑶等国家领导人；中央委员、中央军民军民融合办常务副主任金壮龙，中央委员、浙江省委副书记、省长袁家军等一大批治国栋梁；载人航天工程总设计师王永志、“神舟”五号飞船总设计师戚发轫、航空重点型号总设计师唐长红等18位两院院士；以及大族激光董事长高云峰、新湖期货董事长马文胜等一大批优秀年轻企业家。
学院下设6个实体单位：飞机系、空气动力学系（流体力学研究所）、飞行器结构强度系（固体力学研究所）、人机与环境工程系、飞行力学与控制系、动力学与控制系；涉及3个一级学科:航空宇航科学与技术、力学、动力工程及工程热物理学科，在教育部学位与研究生教育发展中心组织的第四轮学科评估中，航空宇航科学与技术获得一流学科奖（A+类），力学获得（A-类）,两个学科双双被列入教育部一流学科建设名单；涉及10个二级学科，其中流体力学、固体力学、飞行器设计、人机与环境工程学科、工程力学、一般力学及力学基础是国家重点二级学科。
学院建有国家计算流体力学国防科技重点实验室、人机工效与环境控制国防重点学科实验室、粉体技术研究开发北京市重点实验室、流体力学教育部重点实验室、航空科学与技术国家实验室（筹）（飞行器设计基础部）、航空器先进设计技术重点实验室；国家航空航天实验教学示范中心、国家工科基础课程（力学）教学基地、航空科学技术虚拟仿真实验教学中心、（北京）航空航天博物馆、北京市力学实验教学示范中心、航空创新实践基地等。
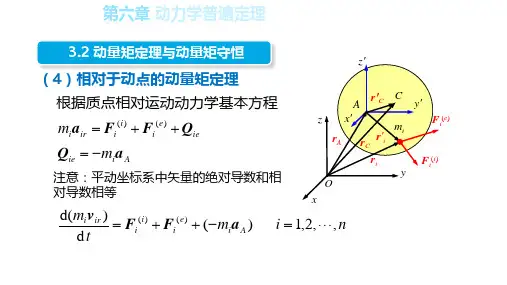
3.2 动量矩定理与动量矩守恒根据质点相对运动动力学基本方程注意：平动坐标系中矢量的绝对导数和相对导数相等(e )（4）相对于动点的动量矩定理iee ii i ir i m Q F F a ++=)()(Ai ie m a Q −=ni m tm A i e i i i ir i ,,2,1)(d )d()()( =−++=a F F v3.2 动量矩定理与动量矩守恒两边叉乘r i ′，并求和（对动点A 取矩）注意到：内力系的主矩等于零；质心计算公式；叉乘性质n i m tm A i e i i i ir i ,,2,1)(d )d()()( =−++=a F F v ()=×′=′=∑∑ir i ir Cii i ie im M m v v r r F[])(d d)(A Ce iiiri iM m ta r Fr v r −×′+×′=×′∑∑是质点系相对动点A是外力系对动点A 的主矩是牵连惯性力的合力对动点A 的力矩注意平动系惯性力合力作用点3.2 动量矩定理与动量矩守恒Ar ir i i m L v r =×′∑ )()(e Ae iiMFr =×′∑ )()(e A A CM Q M a r =−×′d t[∑r i′×m i v ir])(d )(A Ce iiM a r Fr −×′+×′=∑(e )质点系相对动点的动量矩定理＝质点系相对动点的动量矩对时间的导数外力系对该点的主矩加在质心上的牵连惯性力的合力对该点之矩＋3.2 动量矩定理与动量矩守恒3.2 动量矩定理与动量矩守恒①如果动点为质心C ，则动点的动量矩定理为相对质心的动量矩定理)(d d )(e A e A Ar tQ M M L +=3.2 动量矩定理与动量矩守恒②如果a A = 0，则③如果A 点的加速度方向通过质心，则)(d d )(e A e A Ar tQ M M L +=)(d d e A Ar tM L =)(d d e AAr tM L =3.2 动量矩定理与动量矩守恒④对质心的动量矩守恒定律则对质心的动量矩守恒)(d d e CCr tM L =0)(=e CM()=e Cz M cL =cr constL cz =3.2 动量矩定理与动量矩守恒【例】质量为m半径为r的均质圆盘从静止开始，沿倾角为θ的斜面无滑动的滚下。
【北航考研辅导班】北航航天工程（专业学位）考研科目参考书考研大纲考研分数线报录比考研经验一、北航宇航学院简介-启道1956年在我国航天事业创建的同时，北京航空学院（1988年更名为北京航空航天大学）就在国内率先创建了火箭设计和火箭发动机教研室，由屠守锷、曹传钧担任教研室主任；1958年正式组建了火箭系，设有运载火箭设计、有翼导弹设计、液体火箭发动机设计、固体火箭发动机设计、导弹飞行力学、自动控制、发射装置、遥控遥测等专业；1970年由于上级主管部门的变更，学校按学科调整内部结构，将原火箭系各专业划归到有关的系进行管理，并继续为航天技术领域培养人才，进行科学研究；1988年为适应我国航天工业和科学技术发展的需要，学校决定在原火箭系的基础上成立宇航学院。
宇航学院现设有航天飞行器技术系、航天制导导航与控制系、宇航推进系、图像处理中心四个教学科研机构。
拥有飞行器设计与工程（航天）、探测制导与控制技术（航天）、飞行器动力工程（航天）和飞行器控制与信息工程四个本科专业。
拥有航空宇航科学与技术、控制科学与工程二个一级学科，其中航空宇航科学与技术和控制科学与工程为国家重点学科和博士后流动站，且航空宇航科学与技术学科国内排名第一。
拥有飞行器设计、航空宇航推进理论与工程、导航制导与控制、模式识别与智能系统四个博士学位授权点，飞行器设计、航空宇航推进理论与工程、导航制导与控制、模式识别与智能系统四个硕士学位授权点，航天工程专业硕士学位授权点。
以上学科专业均是航天领域的核心学科专业，是航天科技发展的重要支撑。
宇航学院现有教职工127人，其中院士1人、长江学者特聘教授2人、讲座教授2人、国家杰出青年基金获得者1人、人事部百千万人才1人、外专千人2人，教授29人、博士导师29人（其中兼职博导6人）、副教授48人，在站博士后8人，具有博士学位的教师112人，在职教授的授课率达100%。
高水平的师资队伍为学院完成国家赋予的教学、科研任务奠定了人才基础。
质点系动力学在物理学中，质点系动力学是研究物体间相互作用的力以及物体运动轨迹的学科。
本文将讨论质点系动力学中的一个重要概念：刚体运动规律及转动动能定理。
刚体运动规律刚体是一个比较理想化的物理模型，假设物体的形状和大小在运动过程中保持不变。
根据刚体运动规律，刚体在外力作用下会发生运动，根据牛顿第二定律，刚体的运动状态取决于作用在刚体上的合力。
刚体的运动可分为平动和旋转两种类型。
在平动运动中，刚体整体沿直线或曲线运动；而在旋转运动中，刚体绕固定轴线旋转。
根据刚体运动规律，刚体的运动轨迹可以用运动学方程描述，运动方程中包含了速度、加速度等因素。
转动动能定理转动动能定理是描述刚体绕固定轴线旋转动能变化的重要定理。
根据转动动能定理，刚体旋转过程中的动能变化等于作用在刚体上的转动力做功的总和。
假设有一个质量为m、半径为r的刚体，绕垂直轴线（转动惯量为I）旋转。
根据转动动能定理，刚体的转动动能变化ΔK等于转动力做的功W。
转动动能的变化由以下公式给出：ΔK = W = τθ其中，τ为转动力矩，θ为转动角度。
转动角度与角速度的关系为θ = ωt，因此转动动能变化ΔK还可以表示为ΔK = τωt。
结论通过以上讨论，我们了解了质点系动力学中的刚体运动规律以及转动动能定理。
刚体运动规律可以帮助我们理解物体在运动过程中的轨迹和状态变化，而转动动能定理则为解释物体旋转运动提供了重要定量关系。
深入研究质点系动力学中的这些概念，有助于我们更好地理解物体的运动规律和相互作用过程。
在质点系动力学的研究中，刚体运动规律及转动动能定理是重要的基础知识，对于进一步探索物体间相互作用和运动规律具有重要意义。
希望本文的介绍能够帮助读者更好地理解质点系动力学中的这一部分内容，激发对物理学的兴趣和探索。
