质点系动力学能量方法

质点系的动能及动能定理摘要：本文主要探讨质点系的动能及动能定理。

首先介绍了质点系的定义和运动状态，然后阐述了动能的概念及其计算方法。

接下来，通过动能定理解释了外力对质点系动能的影响和相关定理的推导。

最后，结合实例分析了动能的应用和意义。

关键词：质点系；动能；动能定理；外力；定量分析。

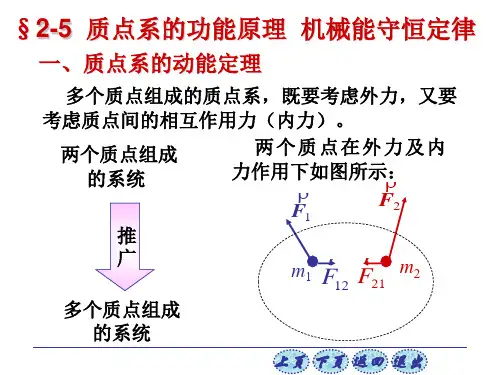
正文：一、质点系的定义和运动状态质点系是指由若干质点组成的物体系统，其中每个质点的质量和运动状态都可以不同。

在研究质点系的过程中，可以通过考虑整体质心的运动状态来简化问题，同时也需要考虑各个质点之间的相互作用力。

二、动能的概念及其计算方法动能指的是物体由于运动而具有的能量，它的大小与物体的质量和速度有关。

对于单个质点，其动能可以表示为：$K=\frac{1}{2}mv^2$其中，$m$表示质点的质量，$v$表示质点的速度。

对于质点系，其总动能可以表示为各个质点动能之和：$K=\sum\frac{1}{2}mv_i^2$其中，$v_i$表示第$i$个质点的速度。

三、动能定理的概念和推导动能定理指的是外力对质点系动能的影响，其表述为：$\Delta K=W$其中，$\Delta K$表示质点系动能的变化量，$W$表示外力对质点系所做的功。

动能定理的推导过程如下：考虑质点系在外力$F$作用下的运动过程，根据牛顿第二定律，可以得到质点系所受的合力为：$F=\sum F_i=ma$其中，$F_i$表示第$i$个质点所受的力，$a$表示质点系的加速度。

假设质点系从时间$t_1$运动到$t_2$，则外力对质点系所做的功可以表示为：$W=F\cdot s$其中，$s$表示质点系在$t_1$到$t_2$时间内所经历的位移。

又因为动能的定义为$K=\frac{1}{2}mv^2$，则质点系的动能变化量可以表示为：$\Delta K=\frac{1}{2}m(v_2^2-v_1^2)$将$t_1$时刻的速度$v_1$视为初始速度，$t_2$时刻的速度$v_2$视为末速度，则根据加速度公式$a=\frac{v_2-v_1}{t_2-t_1}$，可以将动能变化量表示为：$\Delta K=\frac{1}{2}m(v_2-v_1)\cdot(v_2+v_1)$结合外力对质点系所做的功的表达式，可以得到动能定理的表述形式。

第五讲 质点系动能与刚体的动能 2018.11.12一、质点系的动能由于在不同参考系中物体的速度不相同，所以在不同的参考系中物体的动能也一般不同，在同一问题中进行有关功和能的计算时，应选用同一惯性系。

质点系的动能，等于其中各质点动能之和。

设质点系质心的速度为c v ，质点相对于质心速度为i v '，则 c i i i c i i c i k v v m v v m v v m E ⋅'+'+='+=∑∑∑)()(21)(21222， 因为在质心系中质心总是静止不动的，∑='0i i v m ，所以质点系在某参考系中的动能等于质心的动能与在质心系中的动能之和：k c k E Mv E '+=221 其中M 是质点系的总质量，kE '为各质点相对于质心的总动能，这个结论称为柯尼希定理。

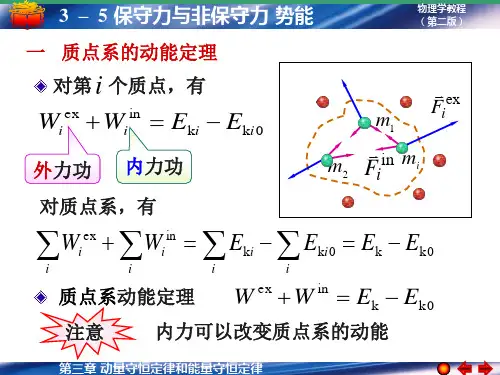
质点系的动能定理：作用在质点系上所有外力和所有内力对质点所做功的代数和，等于质点系总动能的变化，即∑∑∆=+k E W W 内外注意：①对于质点系要考虑内力做功。

只要质点间有相对位移，内力就会对质点做功；②在计算功和能时必须选择同一参考系，且为惯性系。

在非惯性系中应用动能定理，则应考虑惯性力做功。

但在平动质心系中由于各质点所受惯性力可等效作用于质心，质心是静止不动的，因此在平动质心系中不需考虑惯性力做功。

二、刚体的动能刚体绕定轴转动时，设刚体上任一质量元为i m ，它到转轴的距离为i r ，线速度为i v ，则刚体的动能为 222221)2121ωωi i i i i i k r m r m v m E ∑∑∑===（ 即 221ωI E k = 应当注意到，刚体在绕定轴转动时只有转动而没有平动，若一个既在平动也在绕过质心的转轴转动的刚体，它的动能可以由柯尼希定理求得 222121ωI Mv E c k += 上式中，转动惯量I 为刚体绕过质心的转轴旋转的转动惯量，因此上式的适用范围为绕过质心的转轴旋转的刚体。

第十章质点系动力学——能量方法 习题解答10-1半径为r 的匀质圆轮质量均为m ，图（a ）和（b ）所示为轮绕固定轴O 作定轴转动，角速度为ω；图（c ）为轮作纯滚动，轮心速度为v 。

试写出它们的动能。

解：（a ）匀质圆轮作定轴转动， 对O 点的转动惯量为 2222321mr mr mr J O =+=，动能为2224321ωωmr J T O ==。

（b ）匀质圆轮作定轴转动，对O 点的转动惯量为 222121mr mr J O ==， 动能为2224121ωωmr J T O ==。

（c ）匀质圆轮作作纯滚动，ωr v =，动能为222432121mv J mv T C =+=ω10-2匀质杆OA 长l ，质量为m ，绕O 点转动的角速度为ω；匀质圆盘半径为r ，质量也为m 。

求下列三种情况下系统的动能： （1）圆盘固结于杆；（2）圆盘绕A 点转动，相对杆的角速度为ω-； （3）圆盘绕A 点转动，相对杆的角速度为ω。

解：（1）圆盘固结于杆。

对O 点转动惯量为2222221342131mr ml ml mr ml J O +=++=动能为()22223812121ωωm r l J T O +==（2）圆盘绕A 点转动，相对杆的角速度为ω-，则圆盘作平移，质心速度为ωl v =。

动能为： T=T 杆+T 盘=22222223221612121ωωωml mv ml mv J O =+=+（3）圆盘绕A 点转动，相对杆的角速度为ω，则圆盘的角速度为ω2。

T=T 杆+T 盘=()()222222222412*********ωωωωωmr l m ml J mv J C O ++=++()222321ωm r l +=。

10-3质量为m 1的匀质杆，长为l ，一端放在水平面上，另一端与质量为m 2、半径为r 的匀质圆盘在圆盘中心O 点铰接。

圆盘在地面上作纯滚动，圆心速度为v 。

求系统在此位置的动能。

质点动力学和运动物理学的公式和应用物理学是一门自然科学，其中质点动力学和运动物理学是其中非常重要的分支。

质点动力学研究单个物体的运动，在运动物理学中，我们研究宏观物体和大型系统的力学，如汽车、飞机、宇宙航行器等。

本文将讨论一些与质点动力学和运动物理学有关的公式和应用。

一、运动学公式运动学是质点动力学和运动物理学的基础。

在任何物理学中，我们首先通过观察和测量来获得数据，通过对这些数据进行分析和解释，我们可以得到一些重要的物理学定律和公式。

在运动学中，我们主要研究物体的位置、速度和加速度。

以下是运动学公式的一些例子：1. 位移公式：s=vt，其中s表示位移量，v表示速度，t表示时间。

这个公式告诉我们，如果我们知道物体的速度和时间，我们就可以计算出物体的位移。

2. 速度公式：v=ds/dt，其中v表示速度，s表示位移量，t表示时间。

这个公式告诉我们，如果我们知道物体的位移和时间，我们就可以计算出物体的速度。

3. 加速度公式：a=dv/dt，其中a表示加速度，v表示速度，t表示时间。

这个公式告诉我们，如果我们知道物体的速度和时间，我们就可以计算出物体的加速度。

二、牛顿运动定律牛顿运动定律是运动物理学中最重要的定律之一，它描述了力和运动之间的关系。

以下是牛顿运动定律的三个部分：1. 第一定律：一物体，若受力为零，则其静止状态或匀速直线运动状态保持不变。

2. 第二定律：物体的加速度正比于其所受力，反比于物体的质量。

即F=ma，其中F表示力，m表示质量，a表示加速度。

这个公式告诉我们物体的加速度取决于受到的力的大小和方向，以及物体的质量。

3. 第三定律：作用力与反作用力大小相等、方向相反、作用在不同的物体上。

三、动能和势能动能和势能是质点动力学和运动物理学中另外两个重要的概念。

动能是物体运动的能量，势能是物体在某一位置的能量。

1. 动能：动能的公式为K=1/2mv²，其中K表示动能，m表示质量，v表示速度。

质点系统动力学知识点总结质点系统动力学是理论力学的重要组成部分，主要研究多个质点组成的系统在力的作用下的运动规律。

以下是对质点系统动力学知识点的详细总结。

一、质点系统的基本概念质点系统是由若干相互联系的质点组成的系统。

在质点系统中，每个质点都具有一定的质量和位置。

常见的质点系统包括刚体系统、柔体系统等。

刚体系统中，质点之间的距离保持不变；柔体系统中，质点之间的距离可以发生变化。

二、质点系统的受力分析1、外力外力是指来自系统外部的力，如重力、摩擦力、拉力等。

外力的大小和方向会影响质点系统的运动状态。

2、内力内力是指质点系统内部质点之间的相互作用力。

根据牛顿第三定律，内力总是成对出现，大小相等、方向相反，并且在系统的运动分析中，内力的矢量和为零。

三、动量定理1、动量质点的动量等于其质量与速度的乘积，即＄p ＝ mv$ 。

对于质点系统，总动量等于各个质点动量的矢量和。

2、动量定理合外力的冲量等于质点系统动量的增量。

表达式为：＄＼int_{t_1}＾｛t_2} F dt ＝ p_2 p_1$ 。

四、动量守恒定律如果质点系统所受合外力为零，则系统的动量守恒。

即系统的总动量保持不变。

在实际应用中，如碰撞、爆炸等过程，往往可以利用动量守恒定律来分析问题。

五、动能定理1、动能质点的动能等于＄＼frac{1}｛2}mv^2$ ，质点系统的总动能等于各个质点动能的总和。

2、动能定理合外力对质点系统做功等于系统动能的增量。

表达式为：＄W ＝＼Delta E_k$ 。

六、机械能守恒定律如果质点系统只有保守力做功，非保守力不做功，则系统的机械能守恒。

机械能包括动能和势能。

势能常见的有重力势能、弹性势能等。

七、角动量定理1、角动量对于质点，角动量等于位置矢量与动量的叉乘，即＄L ＝ r ＼times p$ 。

2、角动量定理合外力矩的冲量等于质点系统角动量的增量。

八、角动量守恒定律如果质点系统所受合外力矩为零，则系统的角动量守恒。