第一讲 偏好、效用与消费者的基本问题
- 格式:doc
- 大小:569.50 KB
- 文档页数:35

平新乔《微观经济学十八讲》第1讲 偏好、效用与消费者的基本问题跨考网独家整理最全经济学考研真题,经济学考研课后习题解析资料库,您可以在这里查阅历年经济学考研真题,经济学考研课后习题,经济学考研参考书等内容,更有跨考考研历年辅导的经济学学哥学姐的经济学考研经验,从前辈中获得的经验对初学者来说是宝贵的财富,这或许能帮你少走弯路,躲开一些陷阱。
以下内容为跨考网独家整理,如您还需更多考研资料,可选择经济学一对一在线咨询进行咨询。
1.根据下面的描述,画出消费者的无差异曲线。
对于(2)和(3)题,写出效用函数。
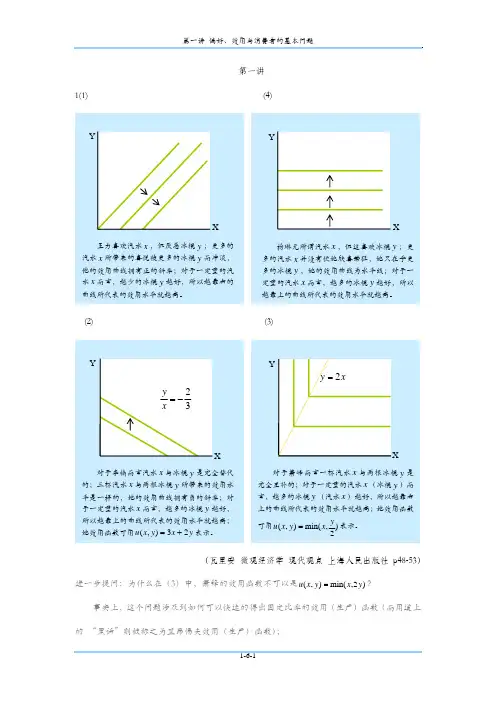
(1)王力喜欢喝汽水x ,但是厌恶吃冰棍y 。
(2)李楠既喜欢喝汽水x ,又喜欢吃冰棍y ,但她认为三杯汽水和两根冰棍是无差异的。
(3)萧峰有个习惯,他每喝一杯汽水x 就要吃两根冰棍y ,当然汽水和冰棍对他而言是多多益善。
(4)杨琳对于有无汽水x 喝毫不在意,但她喜欢吃冰棍y 。
答:(1)根据题意,对王力而言,冰棒是厌恶品,相应的无差异曲线如图1-1所示(图中箭头表示更高的效用方向)。
图1-1 喜欢喝汽水厌恶吃冰棍(2)根据题意,对李楠而言,汽水和冰棒是完全替代品,其效用函数为(),23u x y x y =+,相应的无差异曲线如图1-2所示。
图1-2 既喜欢喝汽水又喜欢吃冰棍(3)消费者对这两种商品的效用函数为(),min ,2y u x y x ⎧⎫=⎨⎬⎩⎭,如图1-3所示。
图1-3 喝一杯汽水就要吃两根冰棍(4)如图1-4所示,其中x 为中性品。
图1-4 对于有无汽水喝毫不在意2.作图:如果一个人的效用函数为(){}1212,max ,u x x x x =(1)请画出三条无差异曲线。
(2)如果11p =,22p =,10y =。
请在图1-5上找出该消费者的最优消费组合。
答:(1)由效用函数画出的三条无差异曲线如图1-5所示。
图1-5 无差异曲线和最优点(2)效用函数确定了消费者的最优选择必定是落在便宜的商品上,即他会将所有收入都用于购买相对便宜的商品,最优点如图1-5中的A 点所示,在该点此人消费10个单位的1x ,0个单位的2x 。





平新乔《微观经济学十八讲》第1讲 偏好、效用与消费者的基本问题跨考网独家整理最全经济学考研真题,经济学考研课后习题解析资料库,您可以在这里查阅历年经济学考研真题,经济学考研课后习题,经济学考研参考书等内容,更有跨考考研历年辅导的经济学学哥学姐的经济学考研经验,从前辈中获得的经验对初学者来说是宝贵的财富,这或许能帮你少走弯路,躲开一些陷阱。
以下内容为跨考网独家整理,如您还需更多考研资料,可选择经济学一对一在线咨询进行咨询。
1.根据下面的描述,画出消费者的无差异曲线。
对于(2)和(3)题,写出效用函数。
(1)王力喜欢喝汽水,但是厌恶吃冰棍。
x y (2)李楠既喜欢喝汽水,又喜欢吃冰棍,但她认为三杯汽水和两根冰棍是无差异x y 的。
(3)萧峰有个习惯,他每喝一杯汽水就要吃两根冰棍,当然汽水和冰棍对他而言x y 是多多益善。
(4)杨琳对于有无汽水喝毫不在意,但她喜欢吃冰棍。
x y 答:(1)根据题意,对王力而言,冰棒是厌恶品,相应的无差异曲线如图1-1所示(图中箭头表示更高的效用方向)。
图1-1 喜欢喝汽水厌恶吃冰棍(2)根据题意,对李楠而言,汽水和冰棒是完全替代品,其效用函数为,相应的无差异曲线如图1-2所示。
(),23u x y x y =+图1-2 既喜欢喝汽水又喜欢吃冰棍(3)消费者对这两种商品的效用函数为,如图1-3所示。
(),min ,2y u x y x ⎧⎫=⎨⎬⎩⎭图1-3 喝一杯汽水就要吃两根冰棍(4)如图1-4所示,其中为中性品。
x图1-4 对于有无汽水喝毫不在意2.作图:如果一个人的效用函数为(){}1212,max ,u x x x x =(1)请画出三条无差异曲线。
(2)如果,,。
请在图1-5上找出该消费者的最优消费组合。
11p =22p =10y =答:(1)由效用函数画出的三条无差异曲线如图1-5所示。
图1-5 无差异曲线和最优点(2)效用函数确定了消费者的最优选择必定是落在便宜的商品上,即他会将所有收入都用于购买相对便宜的商品,最优点如图1-5中的点所示,在该点此人消费10个单位的A ,0个单位的。




中级微观经济学讲义授课教师:葛志杰参考书目清单:1. 平新乔《微观经济学十八讲》北京大学出版社2001版2. 范里安《微观经济学:现代观点》,上海三联出版社,第6版。
3.张维迎《博弈论与信息经济学》,上海三联书店,上海人民出版社。
4. Geoffrey A. Jehle, Philip J.Reny著,《高级微观经济理论》(英文版),上海财经大学出版社。
第一章偏好、效用和消费者的基本问题一、消费集与偏好关系形成需求的三个要素:●消费者对物品的偏好●物品的价格●消费者收入(一)消费集(选择集)X定义:所有可能的(能实现的和不能实现的)消费(选择)方案x的集合。
消费方案x:商品:1) 商品种类为:n2) 商品数量无限可分:i x ∈,商品数量是连续的。
3)商品数量非负:+∈i x4)消费方案 (选择方案,消费束):()1,...,nn x x X +=∈=x消费方案x 特征: 1、 非空集:φ+≠⊆n X2、 闭集:消费集中所有的极限点都包含在该集合中3、 凸集: 任一两个消费计划的凸组合仍包含在该消费集中。
()12,x =∈x x X1x 0 2x 4、包含原点:X 0∈(二)偏好关系1、偏好关系① 偏好关系的定义:定义在消费集X 上,反映X 中任意两个点之间的关系。
12,x x X ,如果有12x x ,则对该消费者而言,“1x 至少和2x 一样好”,或者,“在1x 和2x 之间,消费者弱偏好于1x ”② 偏好关系的特征:满足三个公理:完备性、传递性、连续性公理1:完备性:对于选择集X 中任意的两个要素1x 和2x ,有12xx 或21xx含义:◆消费者能够做出选择◆消费者具有无限的认知能力◆消费者具有无限的判断能力公理2:传递性:对于选择集X中任何的三个要素1x、2x和3x,如果12x x和23x x。
x x,则有13含义:◆消费者的选择具有一致性◆适用条件偏好关系◆(弱)偏好关系:消费集X上的两元关系,如果满足公理一和公理二,就是偏好关系。
理性:公理一+公理二◆严格偏好关系:121221且⇔/x x x x x x◆无差异关系:121221x x x x x x⇔且xxx公理3:连续性: 对于选择集n X +=中的任何元素x ,x 和x 在n X +=中为闭集。
含义:保证了偏好不会出现突发性的逆转。
公理4:无局部飧足点:◆ 飧足点:对于所有的0n +∈x ,有某一个0x x ,x 为飧足点◆ 局部飧足点: 对于0n+∈x ,对于所有的0ε>,在0x 的某个邻域()n B ε+x内,存在着对于所有的n +∈x ,有0x x 。
含义:不存在无差异区域公理4A :严格单调性对于所有的01,n +∈x x ,如果01≥x x ,有01xx ;如果01xx ,有01xx 。
含义: ◆ 多多益善◆ 去掉了无差异曲线上任何一点的右上部分和左下部分1x 2x 公理5:凸性定理:如果1xx ,那么,对于所有的[]0,1t ∈,有()11tx x xx +-=t t 。
公理5A :严格凸性定理:如果11,≠x x xx ,那么,对于所有的()0,1t ∈,有()11x x xx =+-tt t 。
含义: ◆ 平均优于极端◆ 无差异曲线可能凸向原点12x当10x x时,有:0tx x 凸性但非严格凸性当10x x时,有:0tx x 当10x x时,有:0tx x严格凸性二、效用函数(一)定义:实值函数:n u +→,如果对于所有的1,n +∈x x ,有()()011u u ≥⇔xx xx ,则该函数被称为反映偏好关系的效用函数。
意义:将对消费者行为的偏好分析转化为对函数的分析定理1.3:效用函数的正向单调变换不变性定理: 设是n +上的偏好关系,()u x 是反映此偏好关系的效用函数,对于每一个x ,当且仅当()()()v f u =x x ,其中,:f →在定义域上严格递增时,函数()v x 也反映该偏好关系。
常见的单调变换有:1) 对原效用函数乘一个正数2) 对原效用函数加上任意一个数 3) 对原效用函数去奇次幂4) 对数函数与指数函数互为单调变换函数例如:3v u =和5v u =+可能体现同一偏好,只要消费束u 序列相同即可。
(二)边际效用 令12()(,,)n u X u x x x =则12()(,,)i n iMU X u x x x x ∂=∂含义:商品i x 对消费者的效用带来的边际贡献。
(三)边际替代率任意一组消费计划,该消费计划只包含两类商品,1x 和2x ,因21()x f x =又1211()(,)(,())u X u x x u x f x c ===上式两边对1x 求导112()()()u x u x f x x x ∂∂'+=∂∂ 12121()/()()/u x x dx f x u x x dx ∂∂'=-⇒∂∂即∂∂==∂∂()/()()/jiij i jdx u x x MRS x dx u x x边际替代率()ij MRS x 含义: (1)0()ij MRS x(2)()ij MRS x 表示效用水平不变条件下, ix 可以替代jx 的边际比率。
MRS 递减MRS 不变1x 2x 三、消费者的基本问题(一)消费者偏好的基本性质无差异曲线性质: (1) 不同的无差异曲线不相交 (2) 每条无差异曲线严格凸向原点 (3) 越朝东北角,无差异曲线代表的效用水平越高(二)预算集预算集由商品价格向量与消费者收入水平组成。
设价格向量12012(,,),,,,n i p p p p p i n =>=,0p >> 消费者的预算集{},n B x x R p x y +=∈≤1x 2x 2x 1*x(三)消费者的基本问题消费者的问题:max ()..x Bu x s t p x y ∈≤的解:马歇尔需求函数()*,y =x x p112x 1121x 2x 000212(,,)x p p y 100212(,,)x p p y 000112(,,)x p p y 100112(,,)x p p y 002y p 1p 01p 11p1、两维空间:预算线和无差异曲线之间的关系相交→相切→不相交(1)预算线与无差异曲线相切:预算线的斜率:12p p -无差异曲线的斜率:2112dx MU MRS dx MU ==- 121212p dx MU MRS p dx MU -===- 解得马歇尔需求函数()*,y =x x p(2)消费者最优解()*,y =x x p 性质 ● 121212p dx MU MRS p dx MU -===-● 无差异曲线与预算线共有一条公切线 ● 1212λ====nnMU MU MU p p p ,即消费者达到最优时,货币边际效用相等。
2、因已假设效用函数()u x 连续可导,可以用拉格朗日方法求消费者问题的解:()max,u y B ≤∈x px x例题:消费者的效用函数为()11212,u x x x x αα-=,求马歇尔需求函数。
解:设商品1和商品2的价格分别为12,0p p >,消费者收入为0y >。
消费者的决策为:()11212121122max,,..,u x x x x x x s t p x p x y αα-=+=构造拉格朗日函数:()[]112121122,,L x x x x y p x p x ααλλ-=+-- 最优解()12,,x x λ满足一阶条件:()()()1211121111212211122,,0,,0L x x x x p x L x x x x p x p x p x yααααδλαλδδλβλδ----=-==-=+= 解得马歇尔需求函数:()()()11212122,,,,1y x p p y p y x p p y p αα==-。