当前位置：文档之家 › 第3-4章平稳时间序列分析-模型检验.

第3-4章平稳时间序列分析-模型检验.

  • 格式：ppt
  • 大小：428.50 KB
  • 文档页数：48

下载文档原格式

  / 48

合集下载

第四章平稳时间序列模型的建立

第四章平稳时间序列模型的建立

将上式展开得：
xt 1xt1 p xtp 0 at 1at1 2at2 qatq
此时，所要估计的未知参数有p+q+1个.
第二节 模型识别与定阶
一、模型识别 二、模型定阶
一、模型识别
• 基本原则
ˆk
拖尾 q阶截尾
拖尾
ˆkk
P阶截尾 拖尾
拖尾
选择模型 AR(P) MA(q)
ARMA(p,q)
• 序列的非平稳包括均值非平稳和方差非 平稳.
• 均值非平稳序列平稳化的方法：差分变 换.
• 方差非平稳序列平稳化的方法：对数变 换、平方根变换等.
• 序列平稳性的检验方法和手段主要有： 序列趋势图、自相关图、单位根检验、 非参数检验方法等等.
一、平稳性检验—图检验方法
（一）时序图检验
–根据平稳时间序列均值、方差为常数的性 质，平稳序列的时序图应该显示出该序列 始终在一个常数值附近随机波动，而且波 动的范围有界、无明显趋势及周期特征.
–检验1949年——1998年北京市每年最高气温 序列的平稳性
例1 时序图
例1 自相关图
例2 时序图
例2 自相关图
例3 时序图
例3 自相关图
二、纯随机性检验
（一）纯随机序列的定义
• 纯随机序列也称为白噪声序列，它 满足如下两条性质
(1)EX t , t T
(2)
(t,
s)
2,t
s
,
例5、对1950年—1998年北京市城乡居民定期储
蓄所占比例序列的平稳性与纯随机性进行检验
自相关图
白噪声检验结果
延迟阶数 6 12
LB统计量检验
LB检验统计 量的值
75.46
第3-4章平稳时间序列分析-模型检验.

第3-4章平稳时间序列分析-模型检验.


例3.13续：用AIC准则和SBC准则评判例3.13中 两个拟合模型的相对优劣。
模型 MA(2) AR(1) AIC 7.49 7.43 SBC 7.59 7.50
结果： AR(1)优于MA(2)
六、序列预测
所谓预测是要利用序列已观测到的样本值对 序列未来某个时刻的取值进行估计。预测方法主 要有线性最小方差预测和条件期望预测。
i 0 i 0
l 1

2 Gi2
i 0
l 1
当 Gl i Wi , i 0,1, 2,
此时
时，预测方差达到最小，
xt l
的预测值为：
ˆt (l ) W0t W1t 1 x
（2）条件期望预测
xt l t l G1 t l 1 et (l )
ˆ ˆ
t 1 n t 1
nk
t t k
2 ˆ t
例2.5续：检验1950年——1998年北京市城乡居民 定期储蓄比例序列拟合模型的显著性。 残差白噪声序列检验结果： 延迟阶数 6 LB统计量 5.83 P值 0.3229 检验结论
12
18
10.28
11.38
0.5050
0.8361
2 ˆ ˆ t ------残差平和 2 n
T ------待估参数的个数
中心化的ARMA(p,q)模型， T p q 1 非中心化的ARMA(p,q)模型， T pq2
t 1
理论上， AIC和 SBC的值越小越好（注意： 两者皆可为负）。当模型的拟合优度上升时， AIC和 SBC的值会趋于 －∞ 。需注意的是：在 比较两个备选模型的AIC（或 SBC）时，必须基 于相同样本期估计的模型。 SBC具有更优的大样本特性，可以证明， SBC准则是最优模型的真实阶数的相合估计 （一致估计）。而在小样本下AIC效用优于 SBC。一般来说， AIC倾向于选择过多参数的 模型，而SBC倾向于选择更为简练模型。 在使用AIC（或 SBC）准则选择模型时， 我们只能得到相对最优模型，而不可能得到绝 对最优模型。（因为不可能比较所有模型的 AIC值 ）。
时间序列分析第三章平稳时间序列分析

时间序列分析第三章平稳时间序列分析

注：图中，S号代表序列的观察值；连续曲线代表拟合序列曲线；虚线代表拟合序列的95%上下置信限。

所谓预测就是要利用序列以观察到的样本值对序列在未来某个时刻的取值进行估计。

目前对平稳序列最常用的预测方法是线性最小方差预测。

线性是指预测值为观察值序列的线性函数，最小方差是指预测方差达到最小。

在预测图上可以看到，数据围绕一个范围内波动，即说明未来的数值变化时平稳的。

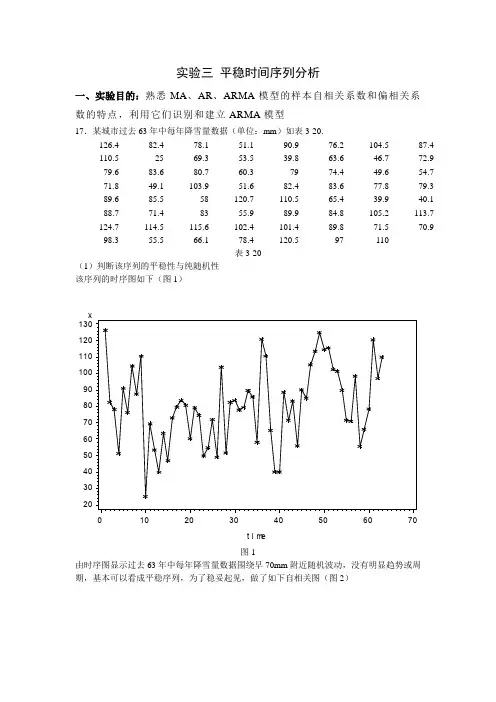
二、课后习题第十七题：根据某城市过去63年中每年降雪量数据（单位：mm）得：（书本P94）程序：data example17_1;input x@@;time=_n_;cards;2579588397 110;proc gplot data=example17_1;plot x*time=1;symbol c=red i=join v=star;run;proc arima data=example17_1;identify var=x nlag=15minic p= (0:5) q=(0:5);run;estimate p=1;run;estimate p=1 noin;run;forecast lead=5id=time out=results;run;proc gplot data=results;plot x*time=1 forecast*time=2 l95*time=3 u95*time=3/overlay;symbol1c=black i=none v=start;symbol2c=red i=join v=none;symbol3c=green i=join v=none l=32;run;（1）判断该序列的平稳性与纯随机性该序列的时序图如下（图a）图a由时序图显示过去63年中每年降雪量数据围绕早70mm附近随机波动，没有明显趋势或周期，基本可以看成平稳序列，为了稳妥起见，做了如下自相关图（图b）图b时序图就是一个平面二维坐标图，通常横轴表示时间，纵轴表示序列取值。

实验三平稳时间序列分析

实验三平稳时间序列分析

84.3
82.9
84.7
82.9
81.5
83.4
87.7
81.879.685 Nhomakorabea877.9
89.7
85.4
86.3
80.7
83.8
90.5
84.5
82.4
86.7
83
81.8
89.3
79.3
82.7
88
79.6
87.8
83.6
79.5
83.3
88.4
86.6
84.6
79.7
86
84.2
83
84.8
83.6
82.1
81.4
85
85.8
84.2
83.5
86.5
85
80.4
85.7
86.7
86.7
82.3
86.4
82.5
82
79.5
86.7
80.5
91.7
81.6
83.9
85.6
84.8
78.4
89.9
85
86.2
83
85.4
84.4
84.5
86.2
85.6
83.2
85.7
83.5
80.1
82.2
88.6
图2
自相关图显示该序列自相关系数一直都比较小，1阶开始控制在2倍的标准差范围以内，可以认为该序列自始自终都在零轴附近波动，这是随即性非常强的平稳时间序列。
纯随机性检验见下图：（图3）
图3
6阶以内P值显著小于0.05，可以认为这个拟合模型的残差序列不属于白躁声序列
（2）如果序列平稳且非白躁声，选折适当模型拟合序列的发展
第4章平稳时间序列预测

第4章平稳时间序列预测

今年第一季度该超市月销售额分别为：
101，96，97.2万元 请确定该超市第二季度每月销售额的预测值.
解: 预测值计算
X t 10 0.6 X t 1 0.3 X t 2 t , t ~ N (0,36) x1 101, x2 96, x3 97.2

四月份: 五月份: 六月份:

方法


第四章 平稳时间序列预测
预测

平稳时间序列预测的定义 利用平稳时间序列{Xt ,t=0,±1,±2,…}在时刻t及以 前时刻 t-1,t-2,…的所有信息，对 Xt+l(l>0)进行估计， 相应的预测量记为
ˆ l ， 称为预测步长，t称为预 X t l
测的原点.
第四章 平稳时间序列预测

ห้องสมุดไป่ตู้
第一节 正交投影预测
统计人数 预测人数
ˆ 2002 104 110 6 2002 x2002 x ˆ 2003 108 100 8 2003 x2003 x ˆ 2004 105 109 4 2004 x2004 x
ˆ2004 (1) 100 0.8 2004 0.6 2003 0.2 2002 109.2 x ˆ2004 (2) 100 0.6 2004 0.2 2003 96 x ˆ2004 (3) 100 0.2 2004 100.8 x ˆ2004 (4) 100 x ˆ2004 (5) 100 x
与预测图(预测1999-2003)
例2：MA(q)模型的预测

已知某地区每年常驻人口数量近似服从MA(3)模型 （单位：万人）：
X t 100 t 0.8t 1 0.6 t 2 0.2 t 3 , 25
平稳时间序列分析

平稳时间序列分析


0
varX t
(1
2 1
2 q
)
2
1
cov( X t , X t1 )
(1
1 2
2 3
q
1
q
)
2
q 1
cov( X t ,
X t q1 )
( q1
1
q
)
2
q
cov( X t , X tq )
q
2
当滞后期不小于q时，Xt旳自协方差系数为0。
所以:有限阶移动平均模型总是平稳旳。
3、ARMA(p,q)模型旳平稳性
• 有时，虽然能估计出一种较为满意旳因果关系回归方程， 但因为对某些解释变量将来值旳预测本身就非常困难，甚 至比预测被解释变量旳将来值更困难，这时因果关系旳回 归模型及其预测技术就不合用了。
在这些情况下，我们采用另一条预测途径：经过时间 序列旳历史数据，得出有关其过去行为旳有关结论，进而 对时间序列将来行为进行推断。
0
2 X
2
12
在稳定条件下，该方差是一非负旳常数，从而有 ||<1。
而AR(1)旳特征方程
(z) 1 z 0
旳根为
z=1/
AR(1)稳定，即 || <1，意味着特征根不小于1。
例 AR(2)模型旳平稳性。 对AR(2)模型
X t 1 X t1 2 X t2 t
方程两边同乘以Xt，再取期望得：
所使用旳工具主要是时间序列旳自有关函数 （autocorrelation function，ACF）及偏自有关函 数（partial autocorrelation function， PACF ）。
1、AR(p)过程
(1)自有关函数ACF 1阶自回归模型AR(1)
chap 3 平稳时间序列分析

chap 3 平稳时间序列分析


32
方差

平稳AR模型的传递形式
xt G j t j
j 0

两边求方差得
2 Var( xt ) G 2 j , G j为Green函数 j 0
33
例3.2:求平稳AR(1)模型的方差

平稳AR(1)模型的传递形式为
t i xt (1B)i t 1 t i 1 1B i 0 i 0

12
AR(P)序列中心化变换

称 { yt }为 {xt } 的中心化序列 ，令

0
1 1 p
yt xt
13
自回归系数多项式

引进延迟算子，中心化 AR( p) 模型又可 以简记为
( B) xt t

自回归系数多项式(特征多项式)
(B) 1 1 B 2 B p B
zt r t (c1eit c2eit ) c3t3 c ptp
16
非齐次线性差分方程的解

非齐次线性差分方程的特解

使得非齐次线性差分方程成立的任意一个解zt
zt a1 zt1 a2 zt2 a p zt p h(t )
11
AR(p)

具有如下结构的模型称为 p 阶自回归模 型，简记为 AR( p) xt 0 1 xt 1 2 xt 2 p xt p t
p 0 2 E ( t ) 0，Var( t ) , E ( t s ) 0, s t Ex 0, s t s t 特别当 0 0 时，称为中心化 AR( p) 模型
37
自相关系数
第三章平稳时间序列分析

第三章平稳时间序列分析

欢迎共阅t P p t tt t t x B x x B x Bx x ===---221第3章 平稳时间序列分析一个序列经过预处理被识别为平稳非白噪声序列，那就说明该序列是一个蕴含着相关信息的平稳序列。

3.1 方法性工具 3.1.1 差分运算 一、p 阶差分记t x ∇为t x 的1阶差分：1--=∇t t t x x x记t x 2∇为t x 的2阶差分：21122---+-=∇-∇=∇t t t t t t x x x x x x 以此类推：记t p x ∇为t x 的p 阶差分：111---∇-∇=∇t p t p t p x x x 二、k 步差分记t k x ∇为t x 的k 步差分：k t t t k x x x --=∇3.1.2 延迟算子 一、定义延迟算子相当与一个时间指针，当前序列值乘以一个延迟算子，就相当于把当前序列值的时间向过去拨了一个时刻。

记B 为延迟算子，有延迟算子的性质：1.10=B2.若c 为任一常数，有1)()(-⋅=⋅=⋅t t t x c x B c x c B3.对任意俩个序列{t x }和{t y }，有11)(--±=±t t t t y x y x B4.n t t n x x B -=5.)!(!!,)1()1(0i n i n C B C B in i i nni i n-=-=-∑=其中二、用延迟算子表示差分运算 1、p 阶差分 2、k 步差分3.2 ARMA 模型的性质 3.2.1 AR 模型定义 具有如下结构的模型称为p 阶自回归模型，简记为AR(p):ts Ex t s E Var E x x x x t s t s t t p tp t p t t t ∀=≠===≠+++++=---,0,0)(,)(,0)(,0222110εεεσεεφεφφφφε(3.4)AR(p)模型有三个限制条件：条件一：0≠p φ。

这个限制条件保证了模型的最高阶数为p 。

第3章平稳线性ARMA模型5模型检验

第3章平稳线性ARMA模型5模型检验

考虑假设检验问题
H0 : j 0 H1 : j 0, 1 j m
9
ARMA(p, q)模型的诊断检验
由于极大似然估计βˆ 为参数β 的渐近无偏估计，
并且具有渐近正态性。因此，记 2vjj 表示V β 的
第 j j 项元素，则 ˆj 渐近分布为 N j ,T 1 2vjj 。
样本残差的自相关系数为
T
ˆtˆtk
ˆk

t k 1 T
ˆt2
t 1
4
ARMA(p, q)模型的诊断检验
构造检验统计量
m
Q T ˆk2 k 1
则检验ˆt 是否为白噪声样本值的问题可转化为检验
统计量 Q 取值的问题。
5
ARMA(p, q)模型的诊断检验
利用 LB(Ljung-Box)检验统计量
AIC 536.4556 535.7896
SBC 543.2011 540.2866
• 结果
ˆ 2 logT p q 1
非中心化的ARMA( p,q )模型SBC为
SBC T logˆ 2 logT p q 2
19
ARMA(p, q)模型的优化
在实际问题中，我们分别计算模型的AIC值和SBC值，比较其大小， AIC值或者SBC值小的所对应的模型较优一些。在所有通过诊断检验 的模型中使得AIC值或者SBC值达到最小的所对应的模型为相对最优 的模型。我们总在尽可能全面的范围内考察有限多个模型的AIC值和 SBC值，选择AIC值和SBC值达到最小的那个模型作为所选的拟合模 型。因此，这样得到的最优模型只是一个相对最优的模型。
14
ARMA(p, q)模型的优化
关于AIC准则，最早是在线性模型中提出的。一般情况下，AIC准 则拟合精度和参数个数的加权函数
第三章 线性平稳时间序列分析

第三章 线性平稳时间序列分析

上海财经大学 统计与管理学院 5
λ + α1λ
p 1
+ + α p = 0
特征根 λ1 , λ2 ,… , λ p 为互不相同的实根 这时齐次线性差分方程的解为 t zt = c1λ1t + + c p λ p 特征根 λ1 , λ2 ,… , λ p 中有相同实根 这时齐次线性差分方程的解为 特征根 λ1 , λ2 ,… , λ p 中有复根 这时齐次线性差分方程的解为
j
j k
根据 Cauchy 不等式,我们可以得到
G j G j k ≤ ∑ G 2 ∑ G 2k ∑ j j j =∞ j =∞ j =∞
∞ ∞ ∞
12
<∞
所以级数
j =∞
∑GG
j∞Leabharlann j k收敛,故 { X t } 为平稳序列.
上海财经大学 统计与管理学院
10
,
3.1.2 线性过程的因果性和可逆性
1 j =1
(3.8)
其中
1 G 1 ( B ) = I ( B) = 1 ∑ I j B j j =1 ∞
(3.9)
称将 X t 变换为 ε t 的线性算子:
I ( B ) = ∑ I j B j , I 0 = 1
j =0
∞
为逆函数 逆函数,称(3.8)为 X t 的逆转形式 逆转形式,也称为无穷阶自回归. 逆函数 逆转形式
j =0 ∞
便于使用的条件是: 便于使用的条件是:
∑ Gj < ∞
∞
j =0
(3.7)
上海财经大学 统计与管理学院 13
在理论研究和实际问题的处理时, 通常还需要用 t 时刻及 t 时刻以前的 X t j ( j = 0,1, ) 来表示白噪声 ε t ,即
第三章 平稳时间序列分析-1

第三章 平稳时间序列分析-1


Φ ( B ) xt = ε t
4、AR模型平稳性判别 、 模型 模型平稳性判别 判别原因 AR模型虽是常用的平稳序列的拟合模型之 模型虽是常用的平稳序列的拟合模型之 一，但并非所有的AR模型都是平稳的 但并非所有的AR模型都是平稳的 判别方法，除时序图及自相关图法外， 判别方法，除时序图及自相关图法外，还有 特征根判别法 特征根判别法 平稳域判别法 平稳域判别法
z t + a1 z t −1 + a 2 z t − 2 + L + a p z t − p = h(t )
齐次线性差分方程
z t + a1 z t −1 + a 2 z t − 2 + L + a p z t − p = 0
齐次线性差分方程的解
z t + a1 z t −1 + a 2 z t − 2 + L + a p z t − p = 0
1+ 3 2
1− 3 λ2 = 2
φ2 = 0.5, φ2 + φ1 = 1.5, φ2 − φ1 = −0.5
作业
P98 习题三 3、4 、 实验1理论（sas简介及数据集创建） 简介及数据集创建） 实验 理论（ 理论 简介及数据集创建
延迟算子的性质： 延迟算子的性质：
B0 = 1
B (c ⋅ xt ) = c ⋅ B( xt ) = c ⋅ xt −1 , c为任意常数
B ( xt ± y t ) = xt −1 ± y t −1
B n xt = xt − n
i (1 − B ) = ∑ ( −1) n C n B i， n i =0 n
则变换y 称为中心化变换 则变换 t=xt-µ称为中心化变换。 称为

第3章平稳时间序列分析


时间序列分析
(1) X t = X t −1 − 0.5 X t − 2 + at
• 自相关函数呈现出“伪周期”性
• 理论偏自相关函数
⎧2 ,k =1 ⎪3 ⎪ φkk = ⎨−0.5 , k = 2 ⎪0 ,k ≥ 3 ⎪ ⎩
• 样本偏自相关图
时间序列分析
(2) X t = − X t −1 − 0.5 X t − 2 + at
由于格林函数描述了系统的动态性，那么在随 机扰动序列已知的情况下，格林函数就完全 能够确定系统的行为，从而根据已知的扰动 序列和格林函数便可确定系统的响应 拟合AR(p)模型的过程也就是使相关序列独立 化的过程.
时间序列分析
• 平稳性的Green函数判别法
欲使序列平稳，则格林函数应满足
当j → ∞时，有G j → 0
ρ k 减小，且以指数速度减小，越来越与0接近，
这种现象称为拖尾.
时间序列分析
4、AR(1)的PACF （1） PACF的求解
AR (1)的 PACF 按照 PACF的递推公式有：
ρ 2 − ρ1φ11 φ12 − φ12 φ11 = ρ1； φ 22 = = =0 2 1 − ρ1φ11 1 − φ1 φ21 = φ11 − φ 22φ11 = φ1 ρ 3 − ρ 2φ 21 − ρ1φ 22 φ13 − φ12φ1 − 0 = =0 φ33 = 2 1 − ρ1φ 21 − ρ 2φ 22 1 − φ1 − 0
时间序列分析
（三）AR(1)的统计特征
1、 AR(1)的方差：
• 平稳AR(1)模型的传递形式为
∞ ∞ at i Xt = = ∑ (φ1 B) at = ∑ φ1i at −i 1 − φ1 B i =0 i =0

第三章平稳时间序列分析-3


n
Q(ˆ )
2 t
t1
n
( xt 1 xt1 p xt p 1 t1 q tq )2 t 1
实际中最常用的参数估计方法是条件最小二乘估 计法
条件最小二乘估计
假设条件：过去未观测到的序列值为0，即
xt 0 , t 0
从而 t
(B) (B) xt
xt
t
i xt1
i 1
由时序图可见，无周期性和单调趋势，序列平稳
序列自相关图
除延迟1阶在2倍标准差外，其它都在2倍标准差范围内 波动，平稳，自相关系数1阶截尾。
所以可考虑拟合模型MA(1)
序列偏自相关图
显然，偏自相关系数拖尾。
【例3.9】 1880-1985全球气表平均温度改变值差分序列
由时序图可见，无周期性和单调趋势，序列平稳
s
t
特别当φ0=0 时，称为中心化ARMA(p,q)模型
系数多项式
引进延迟算子，中心化ARMA(p,q)模型 可简记为 (B)xt (B)t
其中p阶自回归系数多项式：
(B) 11B 2B2 pBp
q阶移动平均系数多项式：
(B) 11B 2B2 q Bq
2、平稳条件与可逆条件
ARMA(p,q)模型的平稳条件 P阶自回归系数多项式Φ(B)=0的根都在单 位圆外,即ARMA(p,q)模型的平稳性完全由 其自回归部分的平稳性决定
Pr
2 n
ˆk
2 n
0.95
Pr
2 n
ˆkk
2 n
0.95
模型定阶的经验方法：
若样本(偏)自相关系数在最初d阶明显大于2 倍标准差，后面几乎95％的值都落在2倍
标准差范围内，且衰减为小值波动的过程 很突然。这时常视为截尾，截尾阶数为d。

第三章平稳时间序列分析

(1)xt 0.8xt1 t (2)xt 1.1xt1 t
(3)xt xt1 0.5xt2 t
(4)xt xt1 0.5xt1 t
例3.1平稳序列时序图
(1)xt 0.8xt1 t
(3)xt xt1 0.5xt2 t
例3.1非平稳序列时序图
(2)xt 1.1xt1 t
❖ 判别方法
▪ 单位根判别法 ▪ 平稳域判别法
自回归方程的解
❖ 任一个中心化 AR( p)模型 (B)xt t都可以视为一个非齐次 线性差分方程，它的通解求法如下
（1）求齐次线性差分方程 (B)xt 0的一个通解 xt
d
p2m
m
xt
cjt
j1 t 1
c
j
t j
rjt (c1 j cos t j c2 j sin t j )
E[(xt Eˆxt )(xtk Eˆxtk )] kk E[(xtk Eˆxtk )2 ]
xt ,xtk xt1 ,
, xtk1
E[(xt Eˆxt )(xtk Eˆxkt E[(xtk Eˆxtk )2 ]
1 1
0 p
Green函数定义
❖ AR模型的传递形式
xt
t
(B)
p i 1
1
ki
i
B
t
p i 1
ki (i B) j t
j0
p
kii jt j
j0 i1
G jt j j0
❖其中系数 {G j , j 1,2,} 称为Green函数
Green函数递推公式
❖ 原理
xt (BG)x(t
❖ 线性差分方程对应的特征根的性质对判断模型的 平稳性有着非常重要的意义

平稳时间序列分析

平稳时间序列分析平稳时间序列分析是一种常用的时间序列分析方法，它旨在研究时间序列在均值和方差上的稳定性，并将其用于预测未来的数据走势。

本文将详细介绍平稳时间序列分析的基本概念、建模方法和预测技术。

首先，让我们来了解什么是时间序列。

时间序列是按照一定的时间间隔收集到的一系列数据点的有序集合，它可以是连续的或离散的。

时间序列分析的目的是通过对过去的数据进行统计分析，揭示出时间序列中的内在规律和趋势，并预测未来的数据走势。

平稳时间序列是指在统计意义上具有稳定性的时间序列，即其均值和方差保持恒定不变。

平稳时间序列具有以下特点：1）均值是常数，不随时间变化；2）方差是常数，不随时间变化；3）协方差只与时间间隔有关，与具体的时间点无关。

为了实现平稳时间序列分析，我们需要进行以下几个步骤：1. 数据准备：收集所需的时间序列数据，并将其整理成适合分析的格式。

通常，我们会绘制时间序列图以直观地查看数据的趋势和模式。

2. 时间序列分解：时间序列通常包含趋势、季节性和随机成分。

我们需要对时间序列进行分解，将其分解为这些组成部分。

常用的分解方法有经典的加性模型和乘性模型。

3. 平稳性检验：对于时间序列分析，我们需要确保数据是平稳的。

平稳性检验的目的是判断时间序列的均值和方差是否是稳定的。

常用的平稳性检验方法有ADF检验、KPSS检验等。

4. 模型建立：如果时间序列被证实是平稳的，我们可以根据数据的模式和趋势选择适当的模型。

常用的模型包括自回归滑动平均模型（ARMA模型）、自回归积分滑动平均模型（ARIMA模型）等。

5. 模型识别与估计：在模型建立的基础上，我们需要对模型进行识别和估计。

模型识别的目的是选择最适合数据的模型阶数，常用的方法有自相关函数（ACF）和偏自相关函数（PACF）的分析。

模型的估计通常使用最大似然估计方法。

6. 模型检验：建立模型后，我们需要对模型进行检验，验证其拟合程度和预测准确度。

常用的模型检验方法有残差分析、DW检验、Ljung-Box检验等。

时序数据分析中的平稳性检验与模型拟合方法

时序数据分析中的平稳性检验与模型拟合方法时序数据分析是一种重要的数据分析方法，它用于研究随时间变化的数据。

在时序数据分析中，平稳性检验和模型拟合是两个关键的步骤。

本文将介绍平稳性检验和模型拟合的基本概念、方法和应用。

一、平稳性检验平稳性是指时间序列数据的统计特性在不同时间段内保持不变。

平稳性检验是为了确定时间序列数据是否满足平稳性的要求。

常用的平稳性检验方法有ADF检验（Augmented Dickey-Fuller test）和KPSS检验（Kwiatkowski-Phillips-Schmidt-Shin test）。

ADF检验是一种常用的平稳性检验方法，它基于Dickey-Fuller单位根检验。

ADF检验的原假设是时间序列数据存在单位根，即非平稳性。

如果通过ADF检验，可以拒绝原假设，认为时间序列数据是平稳的。

KPSS检验是另一种常用的平稳性检验方法，它基于Kwiatkowski-Phillips-Schmidt-Shin统计量。

KPSS检验的原假设是时间序列数据是平稳的。

如果通过KPSS检验，可以拒绝原假设，认为时间序列数据是非平稳的。

平稳性检验的目的是为了确定时间序列数据是否适合进行模型拟合。

如果时间序列数据不满足平稳性要求，就需要进行差分处理或其他预处理方法来使其平稳化。

二、模型拟合方法模型拟合是时序数据分析的核心步骤之一，它用于建立时间序列数据的数学模型，以便对未来的数据进行预测和分析。

常用的模型拟合方法有ARIMA模型（自回归移动平均模型）、GARCH模型（广义自回归条件异方差模型）和VAR模型（向量自回归模型）。

ARIMA模型是一种常用的线性模型，它包括自回归部分、差分部分和移动平均部分。

ARIMA模型适用于平稳时间序列数据的建模和预测。

GARCH模型是一种用于建模条件异方差的模型，它能够捕捉时间序列数据中的波动性。

GARCH模型适用于金融领域的波动性建模和预测。

VAR模型是一种多变量时间序列模型，它能够捕捉不同变量之间的相互关系。

平稳时间序列的判断及建模课件

根据数理统计学知识，显然要分析的随机变量 越少越好，而每个变量获得的样本信息越多越 好。因为随机变量越少，分析的过程越简单， 而样本容量越大，分析的结果就会越可靠。
平稳时间序列的意义
时间序列数据结构的特殊性
可列多个随机变量，而每个变量只有一个样 本观察值
平稳性的重大意义
极大地减少了随机变量的个数，并增加了待 估变量的样本容量
本章结构
平稳性检验 异常点检验与缺省值的补足 纯计量 平稳时间序列的定义 平稳时间序列的统计性质 平稳时间序列的意义 平稳性的检验
特征统计量
平稳性是某些时间序列具有的一种统计 特征。要描述清楚这个特征，我们必须 借助如下统计工具。
运用时间序列模型进行预测的基 本程序
（四）进行参数估计，检验是否具有统 计意义。 （五）进行假设检验，诊断残差序列是 否为白噪声。 （六）利用已通过检验的模型进行预测 分析。
时间序列的预处理
拿到一个观察值序列之后，首先要对它 的平稳性和纯随机性进行检验，这两个 重要的检验称为序列的预处理。根据检 验的结果可以将序列分为不同的类型， 对不同类型的序列我们会采用不同的分 析方法。
平稳时间序列的统计性质
常数均值 EXt ,tT 自协方差函数和自相关函数只依赖于时
间的平移长度而与时间的起止点无关
( t,s ) ( k ,k s t) , t,s ,k T
根据这个性质，可以将自协方差函数由 二维简化为一维，即
(t,s) ˆ(s t), t,s T
特征统计量
均值
t EX t xdt(F x)
方差
D t X E (X tt)2 (xt)2 dt(F x )
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

拟合模型 显著有效
（二）参数的显著性检验
（1）目的： 检验每一个未知参数是否显著非零。删除不显著参 数使模型结构最精简 （2）假设条件：
H0 : j 0 H1 : j 0
（3）检验统计量：
1 j m
T nm
其中
ˆ j j
ˆt2 Q( )
一般地有：
ˆt (l ) 1 x ˆt (l 1) x

x
l 1 t
预测值满足模型差分 方程部分：
ˆt (l ) 1 x ˆt (l 1) 0 x ˆt (0) xt x
AR(2)序列的预测
xt 1xt 1 2 xt 2 t
ˆt (1) E ( xt 1 xt , xt 1 , ) x 1 xt 2 xt 1
例3.13续：用AIC准则和SBC准则评判例3.13中 两个拟合模型的相对优劣。
模型 MA(2) AR(1) AIC 7.49 7.43 SBC 7.59 7.50
结果： AR(1)优于MA(2)
六、序列预测
所谓预测是要利用序列已观测到的样本值对 序列未来某个时刻的取值进行估计。预测方法主 要有线性最小方差预测和条件期望预测。
2 ˆ ˆ t ------残差平方和 2 n
T ------待估参数的个数
中心化的ARMA(p,q)模型， T p q 1 非中心化的ARMA(p,q)模型， T pq2
t 1
理论上， AIC和 SBC的值越小越好（注意： 两者皆可为负）。当模型的拟合优度上升时， AIC和 SBC的值会趋于 －∞ 。需注意的是：在 比较两个备选模型的AIC（或 SBC）时，必须基 于相同样本期估计的模型。 SBC具有更优的大样本特性，可以证明， SBC准则是最优模型的真实阶数的相合估计 （一致估计）。而在小样本下AIC效用优于 SBC。一般来说， AIC倾向于选择过多参数的 模型，而SBC倾向于选择更为简练模型。 在使用AIC（或 SBC）准则选择模型时， 我们只能得到相对最优模型，而不可能得到绝 对最优模型。（因为不可能比较所有模型的 AIC值 ）。
（一）线性预测函数
对于一个平稳可逆的ARMA(p,q)模型来说， 其所有历史未知信息
xt l都可以用已知历史信息
xt , xt 1 ,
表示出来。即
xt l Di xt i
i 0

ˆt (l ) 以 x
D x
i 0

i t i
作为
xt l
的预测值，称
ˆt (l )为 xt 的向前第 l 步线性预测。 x
ˆt (l ) E( xt l xt , xt 1, ) x
对于平稳可逆的ARMA(p,q)模型来说，有
E( xk xt , xt 1, ) xk (k t ) E( k xt , xt 1, ) k (k t )
E( k xt , xt 1, ) 0
E ( xk xt , xt 1 , ) E ( xk t , t 1 , ) xk (k t )
四、模型检验
（一）模型的显著性检验
（1）检验目的 检验模型的有效性（对信息的提取是否充分） （2）检验对象 残差序列 （3）判定原则 一个好的拟合模型应该能够提取观察值序列中几乎 所有的样本相关信息，即残差序列应该为白噪声序列 。 反之，如果残差序列为非白噪声序列，那就意味着残差序 列中还残留着相关信息未被提取，这就说明拟合模型不够 有效。
（4）假设条件 原假设：残差序列为白噪声序列
H0：1 2
m 0, m 1
备择假设：残差序列为非白噪声序列
H1：至少存在某个 k 0, m 1，k m
（5）检验统计量：LB统计量
2 ˆ k 2 LB n(n 2) ( ) ~ (m) ˆk n k k 1 m
i 0 i 0
l 1

2 Gi2
i 0
l 1
当 Gl i Wi , i 0,1, 2,
此时
时，预测方差达到最小，
xt l
的预测值为：
ˆt (l ) W0t W1t 1 x
（2）条件期望预测
xt l t l G1 t l 1 et (l )
xt 1 xt 1 t
ˆt (1) E ( xt 1 xt , xt 1 , ) x E (1 xt t 1 ) xt , xt 1 , 1 xt ˆt (2) E ( xt 2 xt , xt 1 , ) x
E (1 xt 1 t 2 ) xt , xt 1 , 1 E ( xt 1 xt , xt 1 , ) ˆt (1) 1 x 12 xt
6.72
<0.0001
显著
例3.8续: 对OVERSHORTS序列的拟合模型进 行检验。
残差白噪声检验结果：
延迟阶数 6 12 LB统计量 P值 结论
3.15 9.05
0.6772 0.6171
模型显著 有效
参数显著性检验结果：
检验参数 均值 t统计量 －3.75 10.60 P值 <0.0004 <0.0001 结论 显著 显著
由此可见，线性最小方差预测与条件期望
预测是一致的。在正态假定下，有
xt l xt , xt 1,
其中：
ˆt (l ),Var[et (l )]) N (x
ˆt (l ) Glt Gl 1t 1 x et (l ) t l G1t l 1
Gl 1t 1
一般地有，预测值 满足模型差分方程部分：
ˆt (l ) 1x ˆt (l 1) 2 x ˆt (l 2) 0 x
ˆt (2) E ( xt 2 xt , xt 1 , ) x ˆt (1) 2 xt 1 x ˆt (3) E ( xt 3 xt , xt 1 , ) x ˆt (2) 2 x ˆt (1) 1 x
ˆ ˆ
t 1 n t 1
nk
t t k
2 ˆ t
例2.5续：检验1950年——1998年北京市城乡居民 定期储蓄比例序列拟合模型的显著性。 残差白噪声序列检验结果： 延迟阶数 6 LB统计量 5.83 P值 0.3229 检验结论
12
18
10.28
11.38
0.5050
0.8361
（二）预测方差最小原则
预测误差： et (l )
ˆt (l ) xt l x
Varx ˆt ( l ) et (l ) min Var et (l )
由于 x ˆt (l ) 是 xt , xt 1 , 的线性函数，所以
该原理也称为线性预测方差最小原理。
（三）条件 ˆ AIC n ln( ) 2T
AIC 2ln( L) n 2T n 2T 惩罚因子为2 1 n 2 ˆ AIC e n 其中： n ------可用的序列观测值的个数 T ------待估参数的个数
ˆt2------残差平方和 ˆ 2
结论 显著 显著
五、模型优化
问题提出：当一个拟合模型通过了检验，说明 在一定的置信水平下，该模型能有效地拟合观 察值序列的波动，但这种有效模型并不是唯一 的。
优化的目的：选择相对最优模型。
例3.13:拟合某一化学序列(附录1.8)
序列自相关图
序列偏自相关图
拟合模型一 根据自相关系数2阶截尾，拟合MA(2)模型 参数估计：
t 1
n
中心化的ARMA(p,q)模型， T p q 1
非中心化的ARMA(p,q)模型， T pq2
n 1 1 2 l ( , x1 , , xn ) [ ln( ) ln 2 S ( )] 2 2 2
由似然函数可以看出上述三个 统计量会选择相同的模型。
i 0 i 0 j 0 i 0

ˆt (l ) Gi t l i (Gl i Wi ) t i et (l ) xt l x
i 0 i 0
l 1

Var (et (l )) [ Gi2 (Gl i Wi ) 2 ] 2
yieldt 51.17301 (1 0.32286 B 0.31009 B ) t
2
模型检验：模型显著有效；三参数均显著。 拟合模型二 根据偏自相关系数1阶截尾，拟合AR(1)模型
参数估计：
yield t 51.26169
t
1 0.42481 B
模型检验：模型显著有效；两参数均显著。
问题：同一个序列可以构造两个拟合模型，两 个模型都显著有效，那么到底该选择哪个模型 用于统计推断呢？
解决办法：确定适当的比较准则，构造适当的统
计量，确定相对最优。
AIC准则（An Information Criterion）
由日本统计学家赤池弘次（Akaike） 1973年提出，称为最小信息量准则。 如何评价模型对数据的拟合程度？通常 似然函数值越大（或估计的残差平方和越小） 越好。一般地，增加模型中滞后变量的个数 会使估计的残差平方和降低。然而，增加模 型中滞后变量的个数，会使需估计的参数增 多，响应地减少自由度，参数估计的难度越 大，估计的精度越差。甚至，包含了无关紧 要的变量还会降低拟合模型的预测效果。所 以，一个好的拟合模型应该是拟合精度和未 知参数个数的综合最优配置。
预测误差
Glt Gl 1t 1
Gl 1 t 1 Gl t Gl 1 t 1 ˆt (l ) x
预测值

ˆ (l ) E ( xt l xt , xt 1 , ) x Var ( xt l xt , xt 1 , ) Var[et (l )]